亚纯函数与其差分分担值的唯一性

刘彩燕，聂晓汤，林珊华

(1.福建师范大学 数学与统计学院,福建 福州 350117；2.泉州师范学院 数学与计算机科学学院，福建 泉州 362000)

设S是一个复数集合,f(z)和g(z)是两个非常数亚纯函数,定义:

若Ef(S)=Eg(S),则称f(z)和g(z)分担集合SCM(记重数).特别地,当S={a}时,称f(z)和g(z)分担aCM.此外,本文还用到下述定义.

定义1[1]设函数f(z)于开平面亚纯,f(z)的超级如下定义:

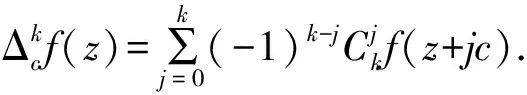
定义2[2]设f(z)为非常数亚纯函数,c∈[JB({〗0},k是正整数,bi(z)∈S(f),i=0,1,2,…,k,且bk(z)≢0.若

P(z,f(z))=bk(z)f(z+kc)+…+b1(z)f(z+c)+b0(z)f(z)，

则称P(z,f(z))为f(z)的k阶线性差分算子.

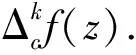
1929年,Nevanlinna[3]利用值分布理论研究亚纯函数唯一性问题,得到著名的五值定理和四值定理,即一个亚纯函数可由其5个IM(不记重数)值点或4个CM(记重数)值点唯一确定下来.其中,亚纯函数与其导函数具有公共值问题是亚纯函数唯一性问题的特殊情况,国内外许多学者对此作出大量的研究工作,取得了有趣的成果[4-5].Gundersen[5]分析和研究了亚纯函数与其导函数分担值的问题,得到下面的结果.

定理 A[5]设f(z)为非常数亚纯函数,a,b,c是三个判别的有穷复数.如果f(z)与f′(z)分担a,b,cIM, 则f(z)=f′(z).

近年来,随着Nevanlinna理论差分模拟[6]的兴起,众多复分析工作者对亚纯函数与其平移算子、差分算子的唯一性问题进行研究,并取得了丰硕的成果[7-12].其中,Heittokangas等[10]取得如下结果.

定理 B[10]设f(z)为有穷级亚纯函数,c∈,是三个不同的以c为周期的周期函数,如果f(z)与f(z+c)分担a1,a2CM,a3IM,则f(z)=f(z+c).

2010年,Zhang[11]进一步考虑了有穷级非常数亚纯函数f(z)与f(z+c)分担集合的唯一性问题,获得如下定理.

2012年,陈宝琴,等[12]考虑有穷级非常数亚纯函数f(z)与其差分算子Δcf(z)的唯一性,证明了:

定理D[12]设S1={1,ω,…,ωn-1},S2={∞},其中ωn=1,且c∈.设f(z)为有穷级非常数亚纯函数,使得Ef(z)(Sj,∞)=EΔcf(Sj,∞)(j=1,2),若n为正整数且n≥7,则Δcf≡tf(z),其中t为满足tn=1的常数且t≠-1.

文中主要考虑两个问题:

问题2定理C、D中的“有穷级”能否去掉.

针对以上问题,研究亚纯函数fn(z),gn(z)具有分担值的唯一性问题,并将其应用到亚纯函数与其差分算子的唯一性问题中.另外,在超级小于1的条件下,探讨亚纯函数与其线性差分算子的唯一性问题.

1 主要引理

引理1[1]设f(z)为非常数亚纯函数,Q(f)=a0fp+a1fp-1+…+ap(a≠0)是关于f(z)的p次多项式,其系数aj(j=0,1,…,p)均为常数,bj(j=0,1,…,q)是q(>p)个判别的有穷复数,则

引理2[1]设f(z)为非常数亚纯函数,aj(j=0,1,…,q)为q(≥3)个判别的复数(其中之一可以为∞),则

引理3[13]设f(z)为非常数亚纯函数且an(≢0),an-1,…,a0是关于f(z)的小函数,则

T(r,anfn+an-1fn-1+…+a1f+a0)=nT(r,f)+S(r,f).

引理4[14]设f(z)为超级ρ2(f)<1的非常数亚纯函数,且c∈[JB({〗0},则

2 结论与证明

本文首先研究两个亚纯函数分担三个值的唯一性问题, 得到了下面的结论.

定理1设f(z),g(z)为非常数亚纯函数,a是非零有穷复数,n为正整数且n≥3.若fn(z)与gn(z)分担aCM,f(z)与g(z)分担0,∞ CM,则或者f(z)=tg(z),其中t为满足tn=1的常数;或者f(z)=beα(z),g(z)=ce-α(z),其中α(z)为整函数,b,c为非零常数且bncn=a2.

证明置

F=fn(z),G=gn(z),

(1)

(2)

由F与G分担aCM,f(z)与g(z)分担∞,0 CM,结合式(2)可知,φ(z)是整函数,从而有N(r,φ)=0,再由引理1可得m(r,φ)=S(r,f)+S(r,g).下面分两种情形讨论.

情形1φ(z)≡0.由式(2)积分得

(3)

其中：C是非零有穷复数.

若C=1,则由式(3)可知F=G,即f(z)=tg(z),其中t为常数且满足tn=1.若C≠1,则由式(3)可知

(4)

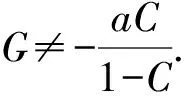
(5)

由第二基本定理及式(5)得

这与n≥3矛盾.

情形2φ(z)≢0.设z0是f(z)的p重极点,则由f(z)与g(z)分担∞ CM知z0也是g(z)的p重极点.由式(2),有z0是φ(z)的零点,且零点的重数至少为np-1,又n≥3,因此

(6)

令

(7)

接下来再分两种情形讨论.

子情形2.1ψ(z)≡0.对式(7)连续积分两次可得

(8)

其中：C1≠0,C2是两个有穷复数.下面对C2分三种情形讨论.

子情形2.1.1C2=0.由式(8),有

(9)

若C1=1,由式(9)可得F=G,即f(z)=tg(z),其中tn=1.

若C1≠1,又C1≠0,由分担条件和a≠0可知G≠a(1-C1),结合n≥3和第二基本定理,类似情形1的证明可推得矛盾.

(10)

若C1=-1,由式(10)可知，FG=a2,即f(z)g(z)=s,其中sn=a2.进一步地,再由分担值条件可知,f(z)和g(z)无零点和极点.因此存在整函数α(z),使得f(z)=beα(z),从而g(z)=ce-α(z),其中b,c为非零常数, 且bncn=a2.若C1≠-1,又C1≠0,则由f(z)与g(z)分担∞ CM可知G≠a(1+C1),结合n≥3和第二基本定理,类似情形1的证明可推得矛盾.

腰椎间盘突出症是骨科的常见病之一，多是由于在外力的作用下，引起髓核突出、压迫神经根所致，可引起一系列症状，如腰痛、腿痛、坐骨神经痛，腰椎活动受限等[1] 。腰椎间盘突出症的治疗方法较多，但目前尚无统一的方案，而手术是一种有效的治疗方法，但术后会造成一定的创伤、引起一些并发症，术后恢复慢[2] ，故而针对此类患者实施康复护理，对于促进疾病的早期恢复有着至关重要的作用。现将笔者的护理体会报告如下。

(11)

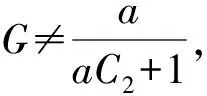
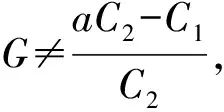
子情形2.2ψ(z)≢0.由式(7)和引理1可得，m(r,ψ)=S(r,f)+S(r,g).再由引理5可知

(12)

由F与G分担aCM,f(z)与g(z)分担0,∞ CM和式(7)可知

(13)

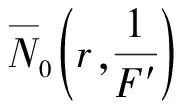
另一方面,由第二基本定理,有

(14)

(15)

注意到

(16)

结合式(12)～(16)可得

将式(6)代入上式可得

(n-2)[T(r,f)+T(r,g)]≤S(r,f)+S(r,g)

与n≥3矛盾.

综上可得,f(z)=tg(z),其中tn=1;或者f(z)=beα(z),g(z)=ce-α(z),其中α(z)为整函数,b,c为非零常数且bncn=a2.

至此,定理1证毕.

基于定理1,本文考察亚纯函数与其差分算子的唯一性问题,得到如下推论.

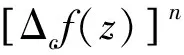
证明由定理1可知,或者f(z)=tΔcf(z),其中t为满足tn=1的常数;或者f(z)=beα(z),Δcf(z)=ce-α(z),其中α(z)为整函数,b,c为非零常数且bncn=a2.

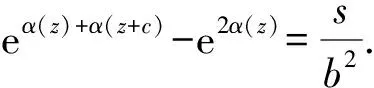
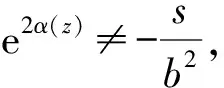
至此,推论1证毕.

进一步结合定义2中的线性差分算子,可得到：

证明由定理1可知,或者f(z)=tP(z,f(z)),其中tn=1;或者f(z)=beα(z),P(z,f(z))=ce-α(z),其中α(z)为整函数,b,c为非零常数且bncn=a2.若f(z)=beα(z),P(z,f(z))=ce-α(z),其中α(z)为整函数,bncn=a2.由f(z)P(z,f(z))≡s,其中s为满足sn=a2的常数,有

进一步地,由f(z)=beα(z)≠0可知

由引理4可得

因此

矛盾.因此f(z)=tP(z,f(z)),其中tn=1.

至此,定理2证毕.