乒乓球运动状态变化的动力学特征及其在搓球和反拉中的应用研究
2022-11-28蒋津君刘妍虹
蒋津君,刘妍虹
正确理解乒乓球球体运动状态变化的动力学特征不仅是提高技术运用合理性的重要前提,也是有效推进乒乓球技术创新的重要基础。前期,虽然已有部分学者对乒乓球球体飞行过程中的受力及其运行轨迹的变化进行过分析,也有少数学者对乒乓球球体在碰撞过程中的受力及其反弹特征进行过研究,但整体上来看,研究点相对较为分散,能有效结合乒乓球运动特征将各个研究点系统地串联到具体技术运用上的研究非常鲜见。这也导致当前诸多著名教练和解说员常常将上升期回击加转弧圈球不易出界和上升期搓球摆短不易下网解释为“在旋转没出来前进行回击”等现象,对诸多技术运用的动力学解释明显不科学。出现以上情况的重要原因之一在于前期乒乓球理论对乒乓球运动状态变化的动力学特征研究较少(乒乓球技术运用动力学特征方面的“理论”明显落后“实践”)[1-4],对相关动力学原理的普及也远远不够。
鉴于此,本研究拟对乒乓球球体运动状态变化的动力学特征进行综合分析,并对其在搓球和反拉中的合理应用进行解释,以期“抛砖引玉”,使教练员和运动员们能更好地把握各项技术运用中球体运动状态的变化规律,正确理解不同技术在实际运用中的合理性,进而为乒乓球的技术创新和科学化训练提供理论参考。
1 乒乓球运动状态变化的动力学特征
1.1 乒乓球在飞行过程中的受力及其运动状态变化特征
关于乒乓球在飞行过程中的受力及其运动状态的变化特征,前期部分研究者已做过理论上的分析,较有代表性的有孙在[5](2008)、严艺[6](2011)、Ralf Schneider[7](2013)、高颖[8](2013)、任艳青[9](2014)、徐家杰[10](2018)等学者,虽然他们对球体的受力及其运行轨迹变化特征的应用点不同,但对于球体在飞行过程中的受力分析基本相同。通过相关物理知识我们可以确定,对飞行中的乒乓球的运动状态产生影响的主要有重力、浮力(几乎可以忽略)、粘滞力、阻力、Mugnus力。
众所周知,球体在空中飞行过程中主要受到重力和气流的作用力,而气流对球体的作用力又可再细分为对球面转动的粘滞力、对球心平动的阻力和Mugnus力等,这些力对球体运动状态改变的作用,需依据球体在飞行过程中的具体情况而定。以下图1中的上旋球为例(V为球心的平动速度,ω为球体的自转速度)。依物理学相关定律和原理,球体在空中飞行的过程中必然会受到重力(G)、浮力(F浮)、与球面转动方向相反的粘滞力(fω)、与球心平动方向相反的空气阻力(F)和Mugnus力(f)。除球体所受重力(G)和浮力(F浮)几乎不变外,其他各力的作用均会随着球体运动状态的改变而有所变化。

图1 乒乓球飞行过程中的受力变化示意图
旋转的球体在飞行过程中受到的Mugnus力(f)的方向会随着其飞行阶段的不同而不断的改变,如上图1所示。在上升期,f对球心平动的作用是向前向下;在高点期,f对球心平动的作用则与重力G的方向一致;在下降期,f对球心平动的作用则是向后向下。即,上升期Mugnus力对球体水平方向的平动有一定的推进作用,而下降期Mugnus力对球体水平方向的平动有一定的阻碍作用;整个飞行过程中,Mugnus力对球体的下落均起加速作用(下旋球则相反)。旋转的球体在空中飞行的过程中,空气对球体表面的粘滞力fω会使球体的旋转速度持续衰减。球越转,球面转动时受到空气的粘滞力相对越大;球面越光滑,球面转动时受到空气的粘滞力相对越小。有研究指出,乒乓球球面相对较为光滑,粘滞力fω对减小球体旋转的实际作用相对较小[6]。
基于以上分析可得:球体脱拍后,在出球角度和球心平动速度相同的情况下,球的上旋越强,其飞行弧线相对越短,弧线的弯曲度也相对越大(下旋越强则球的飞行弧线相对越长,弧线也较平),这也是强烈的上旋球相对不容易出界的主要原因;球在空中飞行过程中,其旋转速度持续缓慢下降;球体在一定方向上的平动速度是否会提高有赖于重力、阻力和Mugnus力在不同方向上的分量大小。同理,球体在与台面碰撞后飞行过程中的受力与之类似。
1.2 乒乓球在碰撞过程中的受力及其运动状态变化特征
1.2.1 乒乓球在碰撞过程中平动量与转动量的相互转换 乒乓球无论是与球台碰撞还是与球拍碰撞,都会产生平动量与转动量的转换,正确认识它们之间的转换关系,有利于我们更好地理解碰撞后乒乓球的速度与旋转的变化。有关于乒乓球在碰撞过程中平动量与转动量的转换原理可作如下简要分析。
如下图2所示(假设球的旋转与球心的运动方向在同一个平面来进行分析,后同),不转球以初速度V0与台面碰撞(即碰撞时球心的初始速度为V0),球心的初速度V0在水平方向上的分量则为V0X,P为球与球台碰撞的接触点。由于球是不转球,碰撞时球面P点相对于台面同样有一个向右的速度V0X,那么在碰撞过程中台面必然会给球面上的P点一个与V0X方向相反的摩擦力F-。由力的平移定理可知,台面给予球面P点的摩擦力可转化为通过球心的力F’并附加一个力偶M,该力偶(M)之距等于摩擦力(F-)与球体半径(R)的乘积。[11]由牛顿定律可知,力F’会使球心在水平方向的平动速度减小,而力偶M则会使球产生Ω方向的转动。即,上述不转球与台面碰撞后,球在水平方向上的平动速度减小的同时还会产生Ω方向的转动。在一定范围内,初速度V0的入射角α的角度越大,平动量转化为转动量的成分越多(这个范围的大小与球和球台之间的摩擦系数有很大的关系,摩擦系数越大,α的角度范围也能越大)。[12]以上所述即为乒乓球在碰撞过程中的部分平动量转化为转动量的基本原理。
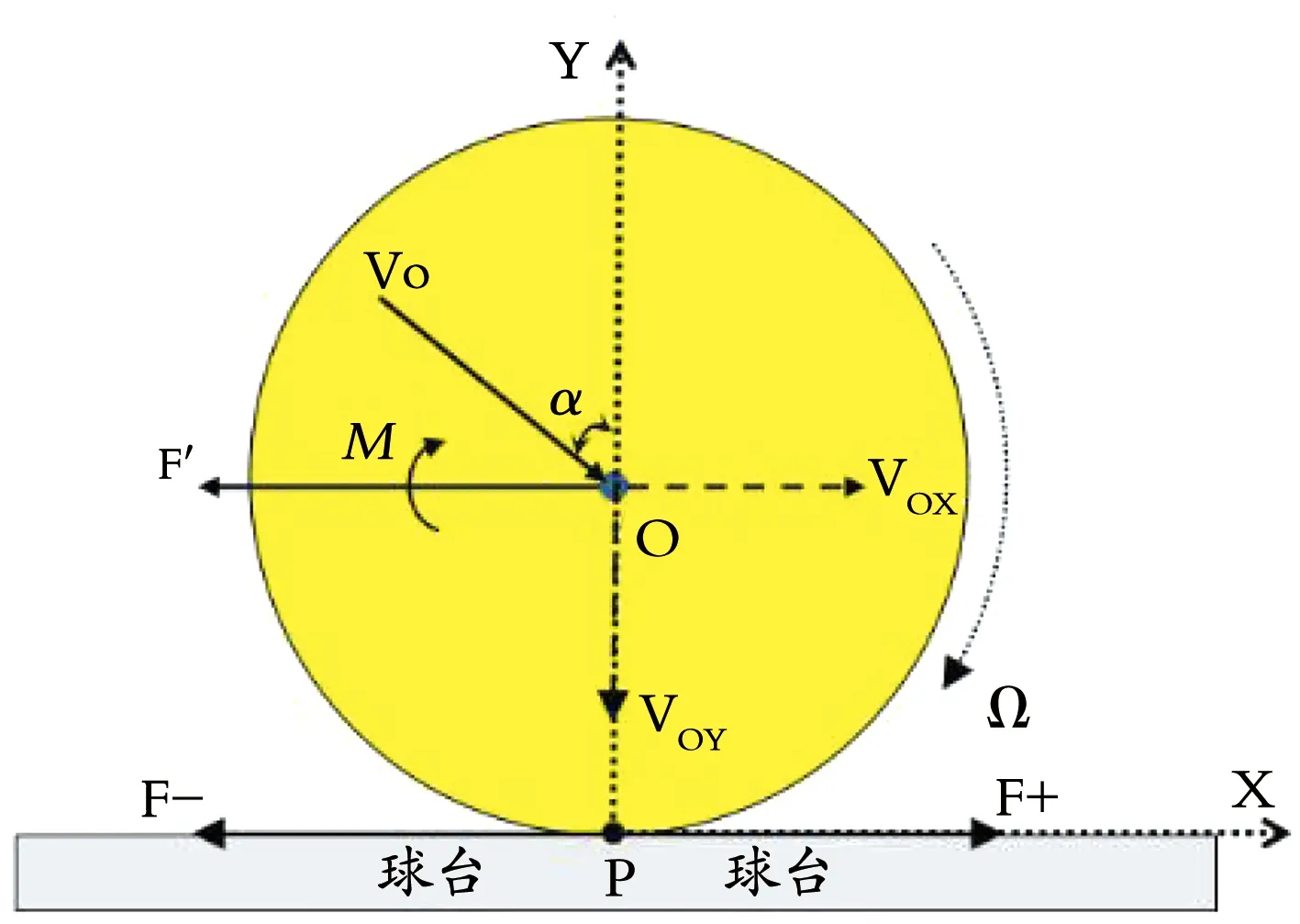
图2 不转球与球台碰撞受力示意图
上图3中所示为Ω方向转动的球以垂直方向(速度为V0)与台面碰撞,由于碰撞时质心速度V0的方向与台面垂直,且球以Ω方向在转动,那么球在与台面碰撞时接触点P相对与台面必然有一个F-方向上的速度,此时球台必然会给予球面上的P点一个与F-方向相反(即F+方向)的摩擦力F+,同样由力的平移定理可知,台面给予球面P点的摩擦力作用可转化为通过球心的力F’并附加一个力偶M,该力偶(M)之距等于摩擦力(F-)与球体半径(R)的乘积。由牛顿相关定律可知,力F’必然会使得球心产生水平方向上的平动,而力偶M则会使球在Ω方向的转动速度减小。即Ω方向转动的球以垂直方向(速度为V0)与台面碰撞后,球的转动速度有所减小,且反弹后的球心会产生水平方向(X轴方向)的速度分量,也即反弹后的球心速度与垂直轴Y会有一个夹角β。碰撞前球旋转的角速度越大,转动量转化为平动的成分越多,反弹角β的角度也越大(角速度需在一定的范围以内,范围的大小与球和球台之间的摩擦系数有很大的关系)[12]。以上所述即为乒乓球的部分转动量转化为平动量的原理。(因以上论述只是为了说明平动量与转动相互转化的一个基本原理,因此并没有把重力、Mugnus力、空气的阻力和粘滞力以及弹跳系数、球体的微形变等这些因素带入分析)

图3 旋转球与球台碰撞受力示意图
实质上,球与球拍碰撞时平动量与转动量的相互转化也是相同原理,不同的是球与球拍碰撞过程中的弹跳系数和摩擦系数有所不同。虽然两类碰撞中平动量与转动量的转化原理相同,但球与球台碰撞时,台面是一直保持水平的,而球与球拍碰撞时拍面的倾斜角度是可以不断变化的,由此分析球与球拍的碰撞会相对较为复杂。
1.2.2 乒乓球与球拍碰撞点的相对速度及其受力特征 击球过程中,因球和球拍的大小、质量、弹性、摩擦系数等指标相对固定,由此,球面与球拍碰撞点的相对速度是分析碰撞过程中球体受力特征的关键。对于球面与球拍碰撞点的相对速度可简要以回搓下旋来球和反拉上旋来球(皆为上升期击球)这两种击球方式为例进行分析。
对于上升期回搓下旋来球时球面与球拍碰撞点的相对速度可作下图4来进行分解分析,结合上升期回搓下旋来球时球和球拍的运动特征可设:P为球面与球拍的碰撞点,球心的平动速度为V0,球拍的挥动速度为V’0,下旋球的转速为ω,球面P点的线速度为Vω。
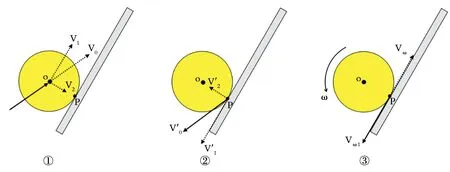
图4 上升期回搓下旋球时碰撞点的相对速度示意图
上图4①中,V1和V2分别为球心的平动速度V0沿拍面方向和垂直拍面方向的正交分解速度;图4②中,V’1和V’2分别为球拍挥动速度V’0沿拍面方向和垂直拍面方向的正交分解速度;图4③中,Vω是由球的转动速度ω产生的球面碰撞点P沿拍面切线方向线速度,而Vω1则是拍面对碰撞点的相对速度(Vω与Vω1的速度值相同,方向相反)。综合各分速度,上升期搓球时,拍面相对球面P点切线方向的合速度值为V1+V’1+Vω1,而碰撞点P相对球拍的正碰合速度值则为V2+V’2(V皆取正值)。
对于上升期反拉上旋来球时球面与球拍碰撞点的相对速度可作下图5来进行分析。同上理,在上升期反拉上旋球时拍面相对球面P点切线方向的合速度值同样为V1+V’1+Vω1,而碰撞点P相对球拍的正碰合速度值也同样为V2+V’2。若是在相同时期拉下旋球,那么拍面相对球面P点切线方向的合速度值则变为V1+V’1-Vω1,而碰撞点P相对球拍的正碰速度值则仍然为V2+V’2(V皆取正值)。

图5 上升期反拉上旋球时碰撞点的相对速度示意图
前期有实验研究指出,球与球拍以不同的相对速度碰撞时,其在碰撞过程中的作用时间相差非常小(即球与球拍碰撞的脱板时间几乎相同)[13-14],由此,球与球拍发生碰撞时的相对速度越大,它们之间产生的作用力也会越大。即,球与球拍碰撞时V1+V’1+Vω1的值越大,球受到拍面的摩擦力相对越大;球与球拍碰撞时V2+V’2的值越大,球受到拍面的正碰力越大。又因,球的大小和质量分布相对固定,由此,摩擦力的大小决定着球体沿摩擦力方向的法向平动速度变化的大小和球面旋转速度变化的大小,而正碰力的大小则决定着球体沿拍面垂直方向反弹速度变化的大小。
基于以上分析可得:球与拍面碰撞时,拍面相对球面碰撞点沿球心方向的正碰速度越大,拍面给予球体的正碰力越大,其对球体沿拍面垂直方向的反弹速度改变越大;球与拍面碰撞时,拍面相对球面碰撞点切线方向的速度越大,拍面给予球体沿碰撞点切线方向的摩擦力则越大,其不仅对球体的旋转速度改变越大,同时对球体沿摩擦力方向的平动速度改变也随之增大。
2 乒乓球运动状态变化的动力学特征在搓球和反拉中的应用
击球瞬间球体相对球台的空间位置、球体的旋转速度、球心的平动速度、挥拍速度、拍面角度、胶皮的弹性和粘性等诸多因素都会影响到最终的击球“质量”和“命中率”,[15]若单单只是提高击球“质量”或“命中率”,诸多回球方式均可实现。然而,更为科学的击球方式是那些能同时兼顾击球“质量”和“命中率”的方式,挖掘这类击球方式是乒乓球技术运用的核心研究内容之一。
2.1 搓球
搓球有快搓和慢搓之分,也有劈长(搓长球)和摆短(搓短球)之分。对于较长的下旋来球,在实战中几乎很少采用摆短(摆短难度也较大),大多是进行抢攻或回搓长球;而对于较短的下旋来球,回搓时劈长或摆短都是常用的手段。由此,分析回搓台内下旋球技术更有实际意义。
2.1.1 上升期与下降期搓球的拍面角度对比 在不考虑球与拍面之间摩擦力的情况下,无论是上升期搓球还是下降期搓球,球与拍面碰撞后的反弹皆为对称反弹,如下图6。球在上升期以速度v0与拍面碰撞,其反弹后的初速度为V1方向;球在下降期以速度u0与拍面碰撞,其反弹后的初速度则为u1方向。即,在不考虑摩擦力的情况下,上升期搓球的反弹更趋向于向上(如图6中V1和u1)。
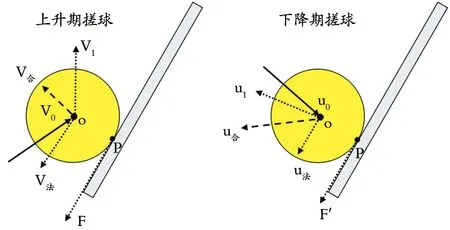
图6 上升期和下降期搓球反弹特征示意图
而在实际当中,球与拍碰撞后的反弹必然要受到摩擦力的影响,结合不同时期搓球球与拍面碰撞时的相对速度来看,在拍面的角度和挥拍速度相近的情况下,上升期球心的平动速度V0的方向相对于下降期u0会更偏离正碰,由此,上升期搓球拍面给予球面碰撞点P的摩擦力整体上会稍大于下降期搓球(F>F’),也即上升期搓球时摩擦力通过碰撞点P给予球体产生平动和转动的法向力整体上会略大于下降期的法向力,再以V法和u法分别结合不计摩擦力时的反弹初速度V1和u1,可得出上升期搓球和下降期搓球的最终反弹速度(速率+方向)分别如上图6中V合和u合。
显而易见,在拍面角度和挥拍速度相近时,下降期搓球时球体的反弹方向(u合)更趋向于向前向下。由此,在下降期进行回搓时拍面的角度需更后仰,否则容易搓球下网。反过来讲,在拍面角度相近的情况下,上升期搓球相对“不易吃转”(不易下网)。由此可知,上升期搓球不易“吃转”的原因并不是在“球的旋转没出来”之前进行回击。实际上,球从台面弹起直至碰到球拍之前,球体的旋转速度是一个持续衰减的过程,不存在“球的旋转没出来”这一提法。
2.1.2 上升期和下降期搓球碰撞点的受力及球的反弹特征 碰撞过程中,球体会受到诸多力的影响,如重力、浮力、空力的阻力和粘滞力等,但以上诸力在球与拍的高速碰撞瞬间对球体反弹的影响可以忽略不计[16],此处不将上述诸力带入分析。
对于上升期和下降期搓球时碰撞点的受力及球的反弹特征,可结合不同时期搓球时球的初速度和拍面角度(下降期搓球拍面角度稍后仰)来进行分析。如下图7,设上升期和下降期球分别以初速度V0和u0与拍面碰撞(N和N’为正碰力),在不计摩擦力F和F’的情况下,球的反弹则分别为V1和u1;加入摩擦力后,若要使球在上升期和下降期搓球的旋转相近,那么使球产生旋转的F和F’的大小则也需相近,而F和F’相近时,它们使球产生旋转的同时给予球心的法向平动速度值也会相近(即V法和u法的速度值相近),那么依速度的合成定律作图后,上升期与下降期搓球时球与拍碰撞后的反弹速度则分别为图7中的V合和u合(V合由V1和V法合成,u合由u1和u法合成)。很明显,在F和F’相近(即让球产生旋转的力相近)的情况下,上升期搓球球的反弹速度V合水平向前的分量值明显会小于下降期搓球的反弹速度u合。即下降期要搓出与上升期旋转相近的球时,球向前的飞行距离会相对偏长。

图7 上升期和下降期搓球碰撞点的受力及球的反弹特征示意图
当然,实际当中F和F’的大小会受到诸多因素的影响(如球面的光滑度、拍面的粘度和侧向弹性系数等),但在这些因素相对固定的情况下(或者说是使用同一个球拍时),其主要影响因素在于碰撞瞬间球的旋转速度和球心相对拍面方向的平动速度(包括球的平动和拍面的挥动)。前期有研究指出,球体在飞行过程中旋转速度的衰减非常小[6],在上升期和下降期击球时间差非常小的情况下,球体旋转速度的衰减几乎可以忽略不计。由此,实际上影响F和F’大小的主要因素就是挥拍速度。
综合以上分析可得出:相对于上升期搓球而言,下降期搓球时球拍的后仰幅度需更大,否则容易搓球下网,而当球拍后仰幅度加大后(挥拍速度不变),拍面给予球面碰撞点的摩擦力向前的成分就会随之增加(如图7中的F’相对于F),且拍面给予球面碰撞点的正碰力向上的成分也会随之增加(如图7中的N’ 相对于N),其最终也会导致下降期搓球球体向前反弹的合速度会大于上降期搓球(如图7中的u合相对于V合)。此时若想要搓出短球,则相对需要降低球拍的挥动速度,而挥拍速度降低后,拍面给予球面的摩擦力也会随之下降,这相对也会降低搓球的旋转。即,相对于上升期搓球而言,下降期搓球相对较难同时兼顾“搓短”和“搓转”两个方面,而上升期搓球则在不降低搓球旋转的同时可将球搓得更短。由此,搓摆加转短球时应尽量在上升期进行击球。
2.2 反拉弧圈球
弧圈球是当前乒乓球比赛中最重要的得分手段之一,而反拉弧圈球(简称“反拉”)又是对付弧圈来球的重要手段之一。反拉弧圈球可分为反拉前冲弧圈球和反拉高吊弧圈球等。本文先主要讨论反拉高吊弧圈球。
2.2.1 不同时期反拉高吊弧圈球的拍面角度对比 相当于前冲弧圈球而言,高吊弧圈球的弧线曲度较大,球体前冲速度较慢,其更强调球体的旋转。通常我们所谈的高吊弧圈球,其球面旋转的线速度要明显大于球心的平动速度,即“球面线速度/球心平动速度”值较大,弧线曲度也相对较大。[17]结合高吊弧圈球的特征,可对不同时期反拉高吊弧圈球的拍面角度作以下对比分析。
高吊弧圈球在飞行过程中的大体运行轨迹及球心在不同时期的瞬时运动方向如下图8,在上升期①附近,球心的运动方向为V①;在高点期②附近,球心的运动方向为V②;在下降期③附近,球心的运动方向为V③。

图8 高吊弧圈球飞行轨迹及不同时期球心瞬时运动方向示意图
结合高吊弧圈球的特征可对其反拉时的拍面角度、挥拍方向作下图9进行分析。图9中V①、V②、V③分别为上升期、高点期、下降期球心的瞬时运动方向;V1、V2、V3分别为拍形1、拍形2、拍形3的挥拍方向。因为是反拉(以摩擦球为主),由此球拍的挥动方向与拍面角度的方向相近,否则就不能称之为“反拉”。

图9 不同时期反拉高吊弧圈球的球心运动方向与拍面角度示意图
由图9可以看出,上升期反拉高吊弧圈球时,拍面可以充分前倾(如图9拍形1)而不用担心拉漏,因为上升期球心的运动方向是迎向拍面(如图9中V①);在高点期反拉高吊弧圈球时可较大程度前倾拍面(如图9拍形2),若过度前倾拍面则容易拉漏;而在下降期(尤其是下降后期)反拉高吊弧圈球时,因球心的运动方向向下(如图9中V③),此时反拉只能稍前倾拍面(如图9拍形3),否则极易拉漏。
2.2.2 不同时期反拉高吊弧圈球碰撞点的受力及球的反弹特征
(1)上升期和下降期反拉高吊弧圈球碰撞点的受力及球的反弹特征。
由前文分析可知,反拉弧圈球时,球与拍在碰撞过程中会受到拍面的正碰力和摩擦力(此时不考虑重力、空气阻力等因素的影响),正碰力会使球体产生垂直拍面方向的平动速度,而摩擦力则使球体产生旋转的同时还使球体产生沿拍面方向的法向平动速度。
结合高吊弧圈球在上升期时球体的运动特征来看,球心向前向上的速度分量明显小于球体表面的线速度,即反拉时拍面通过碰撞点给予球体沿拍面方向的摩擦力要远远大于垂直拍面方向的正碰力。[18]若用拍形1结合V1的挥拍方向在上升期进行反拉,可对球与拍面碰撞过程中的受力及其运动状态变化作如图10分析。

图10 上升期大幅前倾拍面反拉高吊弧圈球时球体反弹特征示意图
图10①中,V’①为球体以平动速度V①与光滑静止的拍面碰撞后的反弹速度(即,先排除球与拍面碰撞过程中的摩擦力和球拍的挥动对球产生的正压力),VN为球拍挥动时对静止的球产生的正压力使球心获得的垂直拍面的速度(相对较小);V法为碰撞过程中摩擦力F法使球心获得的沿拍面方向的法向速度。由速度合成法则可得,V①与VN的合速度为V反,如图10②;而V反与V法的最终合成速度V合则为球体碰撞后最终的反弹速度。
随着挥拍速度的增大(拍面角度和挥拍方向不变),球与拍的正碰速度VN和沿拍面方向的法向速度V法必然随之增大(方向不变),而V’①则不变。因击球方式是以摩擦为主,由此VN的增幅要明显小于V法。随着VN略有增大,由VN和V’①产生的合速度V反大体上会有如下图11所示的细微变化,而V法的增幅则较大。又因球体反弹后的最终速度V合是由V反与V法合成,那么球体与不同速度的球拍摩擦碰撞后的最终反弹速度必然有如下图11中V合1、V合2、V合3所示的变化特征。

图11 上升期大幅前倾拍面以不同挥拍速度反拉高吊弧圈球时球体反弹速度变化示意图
同理,在下降期以拍形3和的挥拍方向V3进行反拉时,球与拍面碰撞受力后的反弹速度V合则有如图12①、图12②所示的特征。而球体与不同速度的球拍碰撞后的最终反弹速度则大体上有如图12(3)中V合1、V合2、V合3所示的变化特征。

图12 下降期稍前倾拍面反拉高吊弧圈球时球体反弹特征示意图
显然,无论是在上升期以大幅度前倾拍面(拍形1)的形式进行反拉,还是在下降期以稍前倾拍面(拍形3)的形式进行反拉,在挥拍速度不是过小的前提下,球拍的挥动速度对球体脱板瞬间的反弹方向影响相对较小。不同的是,以拍形1在上升期进行反拉,球体的反弹方向皆是以向前为主,而下降期以拍形3进行反拉,球体的反弹方向则是以向上为主,如上图11和图12③所示。图11中,随着挥拍速度加大,球体向前的反弹速度(V合)越大,旋转越强,同时球体飞行过程中气流给予球体向下的压力(Mugnus力f)越大[6];图12③中,随着挥拍速度加大,球体向上的反弹速度(V合)越大,旋转越强,球体飞行过程中气流给予球体向前下方的压力(Mugnus力f)越大。结合高速挥拍击球后球体的反弹方向来看,在下降期以拍形3反拉时的挥拍速度稍大(球脱拍后向上的速度分量也会较大),反拉时容易出界,如下图13所示。而以拍形1在上升期反拉高吊弧圈球,则相对能更好地兼顾击球的质量和命中率,其发力击球时的“容错率”要明显高于下降期反拉。

图13 上升期和下降期以不同挥拍速度反拉高吊弧圈球时球体反弹运行轨迹变化示意图
(2)高点期反拉高吊弧圈球碰撞点的受力及球的反弹特征。
结合前文对反拉高吊弧圈球时球与拍碰撞过程中的受力和反弹特征的分析来看,在高点期采用较前倾拍面的形式(拍形2)进行反拉,发力稍大时同样容易出界(因球与拍碰撞后的初速度向上的成分同样较大),但其相对要好于下降期以拍形3进行发力反拉。若是错过了上升期,在高点期如何回击相对能较好地兼顾击球“质量”和“命中率”呢?
结合反拉高吊弧圈球(摩擦为主)球体最终反弹方向的变化趋势可发现,反拉时拍面越前倾,球体的反弹方向越趋于向前。若想在高点期发力反拉而球不易出界,则需使球体最终的反弹合速度趋向于前下方,那么单从球体碰撞后的反弹特征来看,采用下图14①所示的拍形0结合向前下方(V0)的挥拍方式进行反拉同样也可以较好保证击球的命中率。但在实际当中,该击球方式相对于上升期反拉会有以下劣势:①这种由上向下以摩擦为主的挥拍方式相对较难充分发挥蹬腿的力量;②在挥拍速度相近时,球体最终的反弹合速度值V合明显小于V法,即球体最终的反弹合速度与挥拍速度的差值略大(球体前冲的合速度值相对稍小),如图14②所示;③当挥拍方向V0与拍面前倾方向相接近,反拉时相对容易漏球,而当挥拍方向与拍面前倾角度相差较大时,球体最终的反弹方向会随着挥拍速度的不同产生较大偏差(容错率会相对降低)。当然,高点期反拉相对于上升期反拉也有其自身的优势,那就是有更充分的引拍时间(可更好发力)和判断来球旋转的时间。
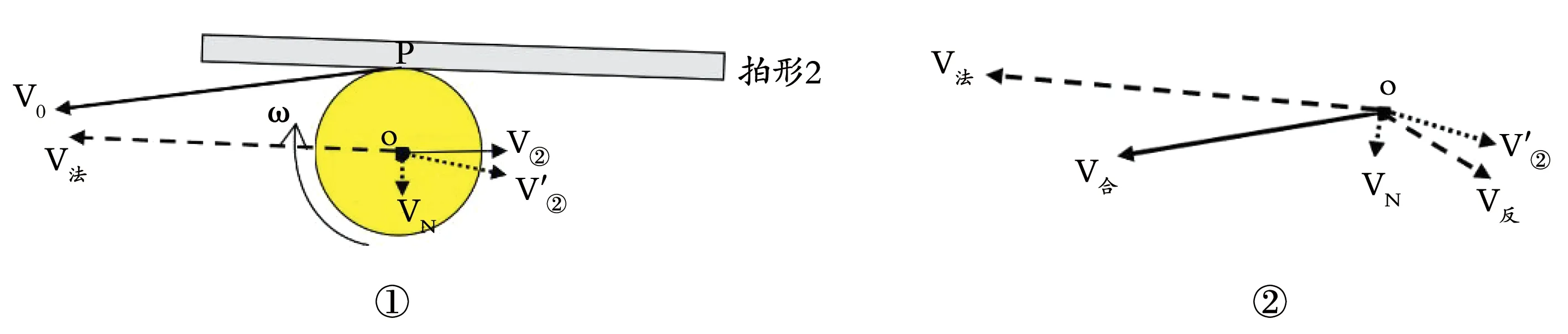
图14 高点期大幅前倾拍面反拉高吊弧圈球时球体反弹特征示意图
由此,错过上升期后,在高点期附近采用图14①所示的方式进行反拉也是一个较好的选择,其在不“拉漏”的前提下同样也可较好地保证击球的命中率。
除了以上方式外,在高点期也可采用较大前倾拍面(类似拍形2)结合高速撞击的形式来进行回击,具体如下图15所示(虽该击球方式不在反拉讨论范围,但对其进行补充分析有助于更好理解球体运动状态变化的动力学特征,在此对该方式作一个附加分析)。
结合高吊弧圈球的球体运动特征来看,在高点期采用图15①中的拍形2结合V2的挥拍方向进行击打回球时,对球与拍面碰撞过程中的受力及其运动状态变化可作如下分析。图15①中,V’②为球以平动速度V②与光滑静止的拍面碰撞后的反弹速度(即不考虑球与拍面碰撞过程中的摩擦力和球拍的挥动对球产生的正压力),VN为球拍挥动时对静止的球产生的正压力使球心获得的垂直拍面的速度;V法为碰撞过程中摩擦力F法使球心获得的沿拍面方向的法向速度。由速度的合成法则可得,V’②与VN的合速度为V反,而V反与V法的最终合成速度V合则为球体碰撞后的最终速度,如下图15②。
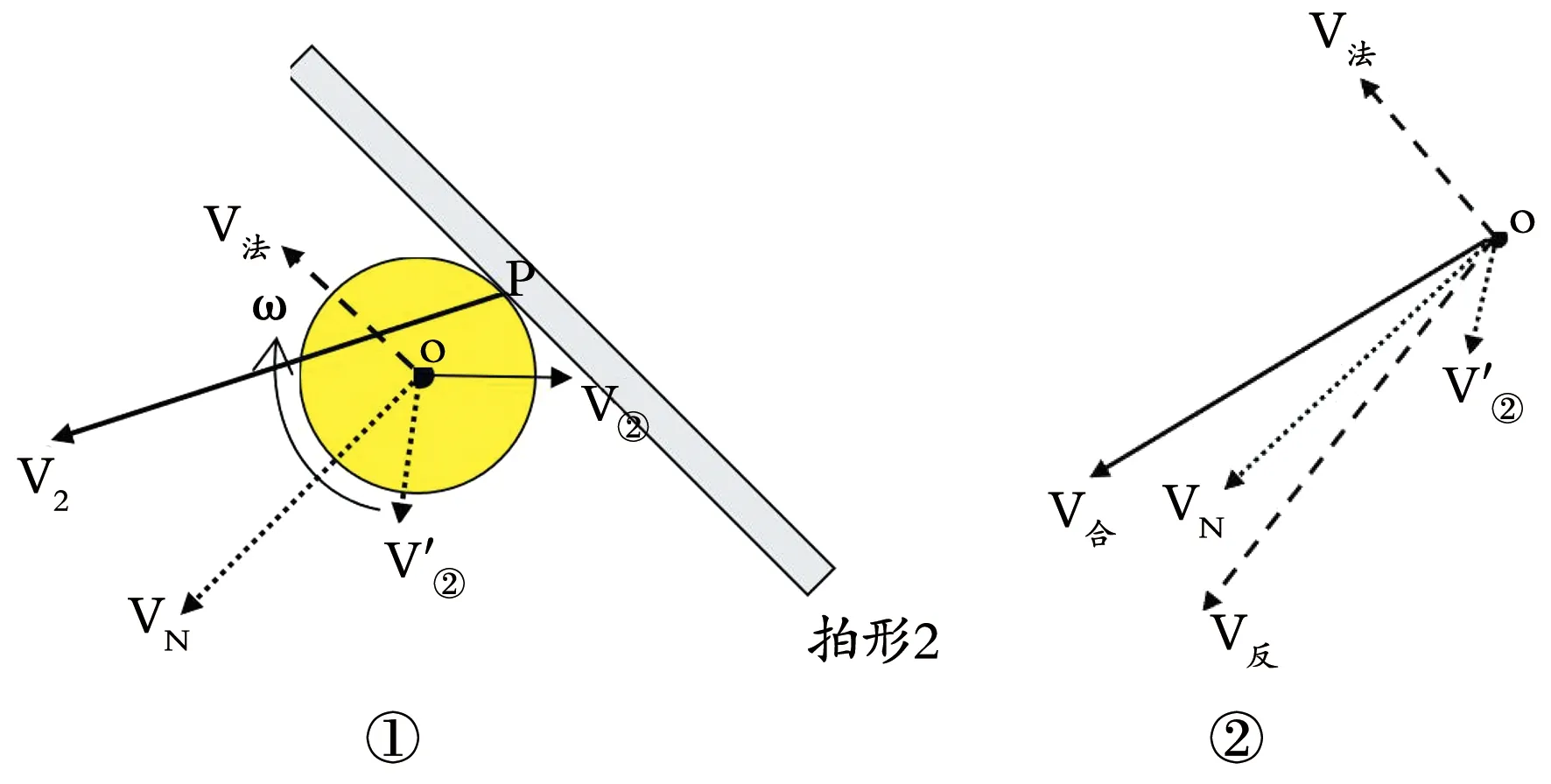
图15 较大前倾拍面在高点期击打高吊弧圈球时球体反弹特征示意图
结合撞击击球方式的各项速度特征来看,随着挥拍速度V2增大,上图15①中的VN和V法必然随之增大,又因是以撞击为主(挥拍方向较接近垂直拍面方向),由此VN的增大幅度会明显大于V法(V法的变化与摩擦力直接相关,此时的V法主要由球体自身的旋转而产生);再结合VN和V’②合成速度V反来看,随着挥拍速度值的增大,V反的增大幅度同样会明显大于V法,如下图16所示。
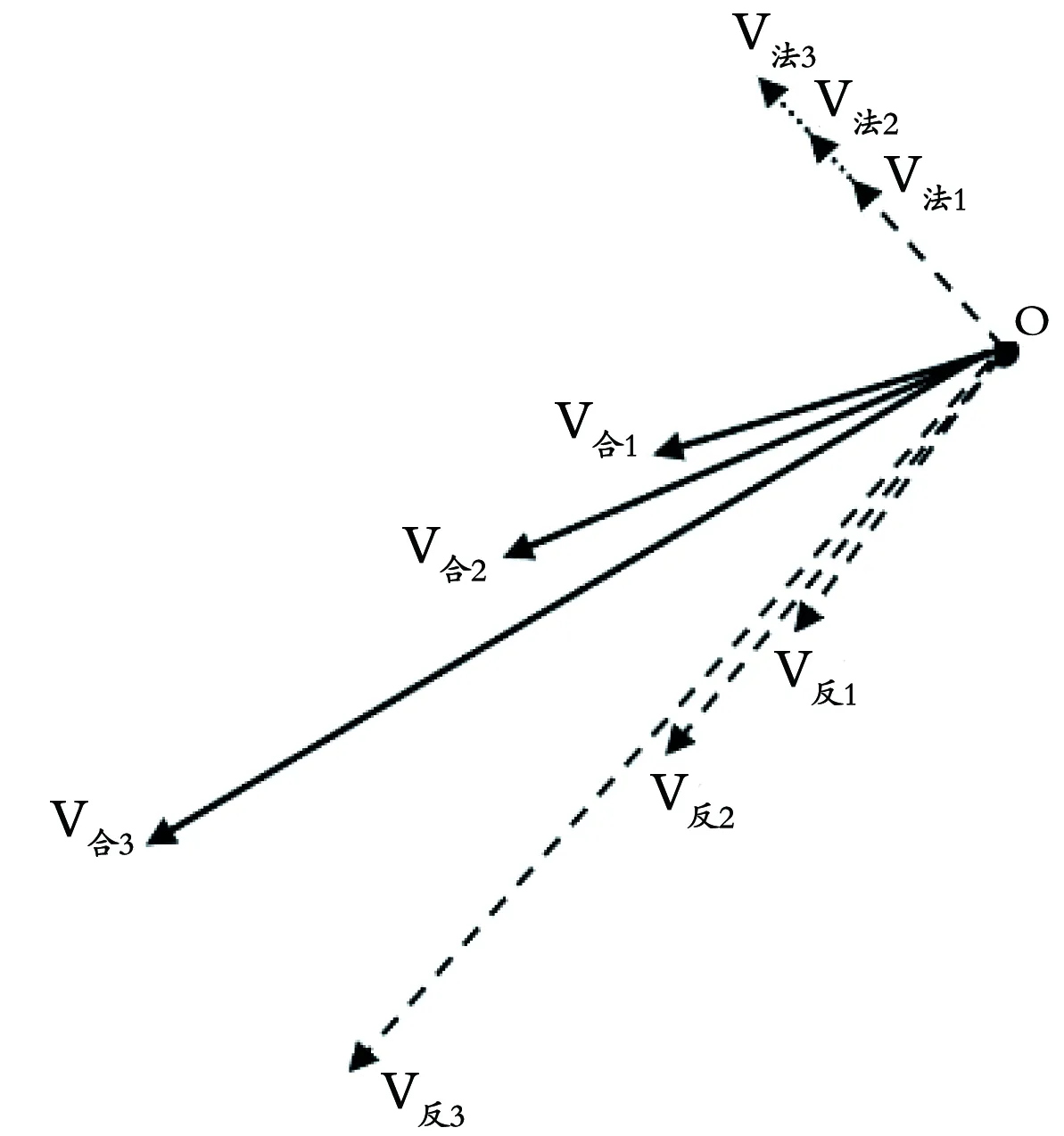
图16 较大前倾拍面以不同挥拍速度在高点期击打高吊弧圈球时球体反弹速度变化示意图
结合上述分析来看,随着挥拍速度的增大,V法只可能是稍有增大(如图16中V法1、V法2、V法3所示),而V反的增大幅度则明显较大(如图16中V反1、V反2、V反3所示)。由此,随着挥拍速度的增大,球体最终的反弹速度V合(由V反和V法合成)必然会有如上图16中V合1、V合2、V合3所示的变化趋势。显然,随着挥拍速度的增大,球体与拍面碰撞后的反弹速度不仅会随之增大,其反弹方向也会越趋近于垂直拍面方向(越能“抵消”来球的上旋),这也是我们常常提到的以高速撞击来克服旋转的击球方式。由此来看,在高点期以较大前倾拍面结合高速撞击的形式来回击高吊弧圈球同样是一个较好的选择。当然,此种击球方式更适合于“弧线较高的来球”(因其在高点期击球时,击球点的高度会明显高于球网),而对于弧线较低的“小高吊”球,此种击球方式的“容错率”同样会有所降低。
3 结论与建议
3.1 结 论
(1)球体在空中飞行过程中,其自身的旋转速度持续衰减;因球面相对较为光滑,球体在飞行过程中的旋转速度衰减相对较慢。
(2)球体与台面或拍面碰撞时,存在不同程度的平动量与转动量的转化;碰撞过程给予球面的摩擦力不仅使球体产生转动,也使球体产生沿摩擦力方向的平动,即,借助球体自身的旋转来增大击球时球与拍面的摩擦力,可使回球的旋转速度和平动速度同时增大。
(3)相对于上升期搓球而言,下降期搓球相对较难同时兼顾“搓短”和“搓转”两个方面,而上升期搓球则在不降低搓球旋转的同时可将球搓得更短。
(4)在上升期以大幅前倾拍面的形式反拉高吊弧圈球,相对能更好地兼顾击球的“质量”和“命中率”;高点期反拉次之,而在下降期反拉高吊弧圈球则相对较难兼顾击球的“质量”和“命中率”。
(5)球与拍碰撞过程中的正碰力越大,球体脱拍后的运动方向越趋近于垂直拍面方向,以高速撞击的方式击球能一定程度上“克服”来球的旋转。
3.2 建 议
(1)单单通过延缓击球时间来降低接球的“吃转”程度并不会取得较好效果,想要降低接球的“吃转”程度需综合考虑不同时期球体的平动方向和旋转方向、击球瞬间的拍面角度以及挥拍的速度和方向等各方面的因素来进行调整。
(2)回击旋转较强的来球时,可借助球自身的旋转来增大球与拍面碰撞时的摩擦力(例如反拉高吊弧圈球),其不仅可有效将球体的转动量转化为平动量(提高回球的飞行速度),同时还能有效增强回球的旋转。
(3)“回搓摆短”台内下旋来球时,尽量在来球的上升期进行搓摆;反拉高吊弧圈球时宜在来球反弹的上升期进行反拉;若是错过反拉高吊弧圈球的最佳时期(上升期)或是有意改变一下击球节奏,对于弧线较高的来球也可在高点期采用大幅前倾拍面结合向前下方挥拍的形式进行反拉或以较大前倾拍面结合撞击为主的方式进行回击;而在下降期(尤其是下降后期),回击高吊弧圈球时不宜发力过大,用中小力量将球“护”过去相对更为合理。
(4)正确认识乒乓球球体运动状态变化的动力学特征是有效把握合理击球方式基础。若乒乓球技战术的训练只靠“经验”而缺乏科学的理论依据作支撑,其不仅不利于技术创新,还可能对后续技术的正确运用产生“误导”作用。由此,我们需要进一步加强乒乓球运动的力学特征研究并进行有效普及。
