时间尺度上Whittaker 方程的Noether 对称性与守恒量

舒莲莲，朱建青

(苏州科技大学 数学科学学院，江苏 苏州 215009)

1918年，Noether 建立了Noether 理论[1].1988年，Hilger 对时间尺度理论有了初步研究，Agarwal 和Bohner[2]研究了时间尺度上的基本运算法则，并推导了部分定理.之后对于时间尺度的研究快速发展，并广泛应用在量子力学、自然科学、经济学等领域[3-5].Bartosiewicz 和Torres[6]首次研究时间尺度上的Noether 定理.Cai等[7]将时间尺度理论和Noether 对称性理论结合，得到了Lagrange 系统中计算第一积分的方法.Peng等[8]将Noether 和Lie 对称性方法运用到时间尺度上的Hamilton 系统，导出Noether 守恒量.近年来，众多学者为将不同力学系统的对称性与守恒量推广到时间尺度理论，做出很多科研成果[9-12].

在物理、工程、生物等领域的数学建模中，大多需要通过微分方程来表述.因此对于微分方程的构造约化、求解等很有必要，而利用对称性获取守恒量求解微分方程是一个灵活有效的方法.Bhutani 和Mital[13]利用Noether 对称性，讨论了Shallow-membrane 方程的第一积分.梅凤翔[14]研究了Emden 方程的不同表达形式，有不同的对称性.张毅[15]用著名的van der Pol、Duffing 等弱非线性方程作为实例，分析了它们的Noether 准对称性与近似Noether 守恒量.1904年，Whittaker[16]利用能量积分把完整保守力学系统降阶为基于更少的自由度系统，得到Whittaker 方程.Whittaker 方程不仅可以处理Lagrange 力学逆问题，还可以为工程实际应用中的构造模型提供数学工具等[17-18].梅凤翔、丁光涛等[19-20]对构造Whittaker 方程的Lagrange 函数、Hamilton 和Birkhoff 函数做了进一步研究.本文利用Noether 对称性研究时间尺度上Whittaker 方程的守恒量，首先考虑力学化后的Whittaker 方程可取得力学函数，再根据力学系统的Noether理论，讨论时间尺度上Whittaker 方程在Lagrange、Hamilton 及Birkhoff 三大力学体系下的关系，最后灵活得到方程守恒量.

1 Whittaker 方程在Lagrange 系统下的Noether 定理

时间尺度上Whittaker 方程为

Whittaker 方程可部分Lagrange化，得到Lagrange 函数和广义力分别为[20]

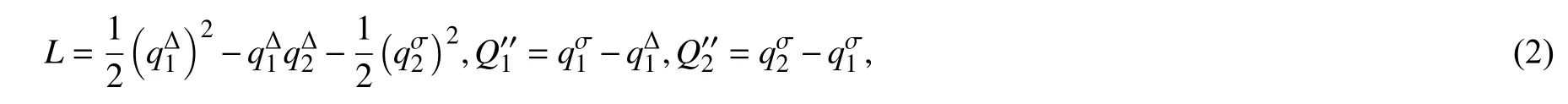
则Whittaker 方程的Hamilton 作用量为

再利用时间尺度理论的计算法则，类似于文献[7]，则Whittaker 方程可化为时间尺度上一般完整系统的Lagrange 方程，即

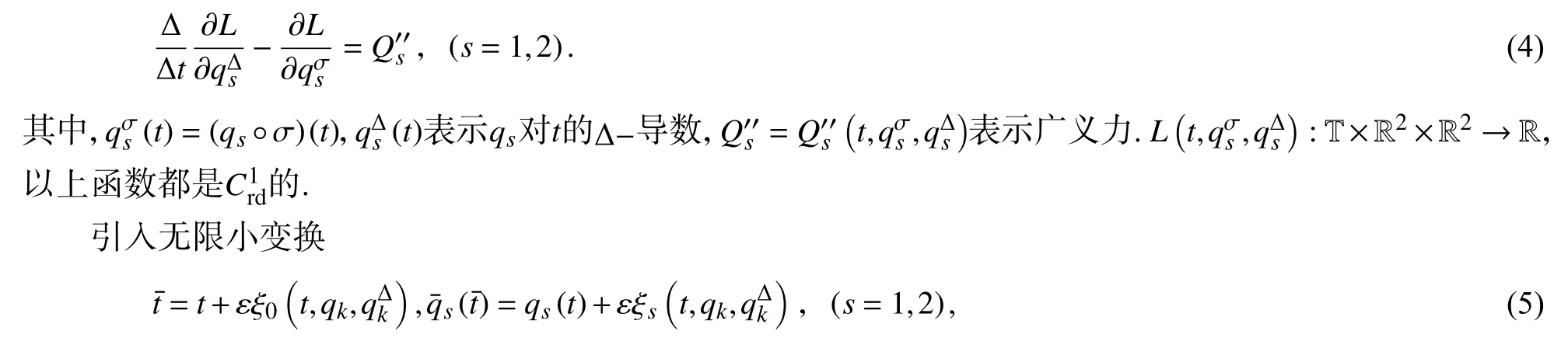
其中，ε是无限小参数，ξ0，ξs是生成元.

定义1Hamilton 作用量(3)在变换(5)下的不变性是时间尺度上Whittaker 方程相应于Lagrange 系统下的Noether 对称性.

则此不变性是时间尺度上Whittaker 方程相应于Lagrange 系统下的Noether 对称性.

定理1对于Whittaker 方程在Lagrange 系统下，若变换(5)的生成元 ξ0,ξs使广义Noether 等式(6)成立，则此系统有Noether 守恒量

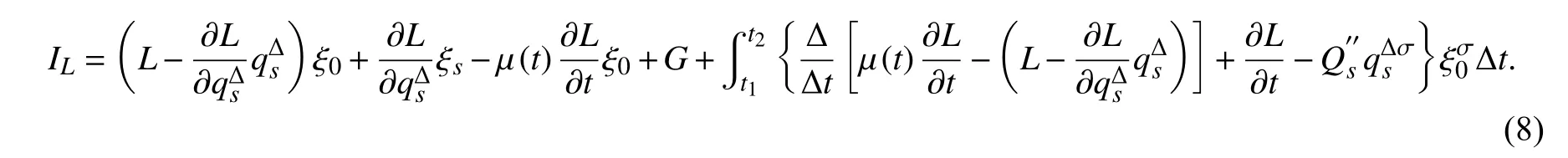
证明将式(8)两边对t求Δ-导数，并利用方程(4)和式(6)，可得

因此(8)式是该系统的守恒量.证毕.

2 Whittaker 方程在Hamilton 系统下的Noether 定理

将时间尺度上Whittaker 方程力学化在力学体系中，则可利用其分析力学体系的性质，方程在Lagrange 体系下可进行转化为等价于Hamilton 体系下的形式，结合(1)和(2)式，令

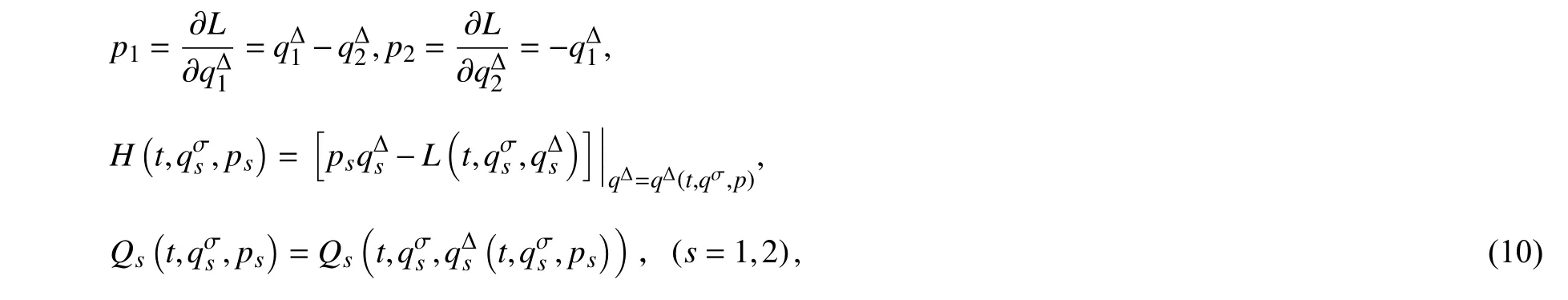
则Whittaker 方程的Lagrange 函数和广义力(2)式对应等价的Hamilton 函数和广义力为

即Whittaker 方程在相空间中Hamilton 作用量为

Whittaker 方程可以正则化为时间尺度上相空间一般完整系统的Hamilton 方程，即

则此不变性是时间尺度上Whittaker 方程相应于Hamilton 系统下的Noether 对称性.

定理2对于Whittaker 方程在Hamilton 系统下，若变换(14)的生成元 ξ0,ξs使广义Noether 等式(15)成立，则此系统有Noether 守恒量

证明将式(17)两边对t求Δ-导数，并利用方程(13)和式(15)，可得

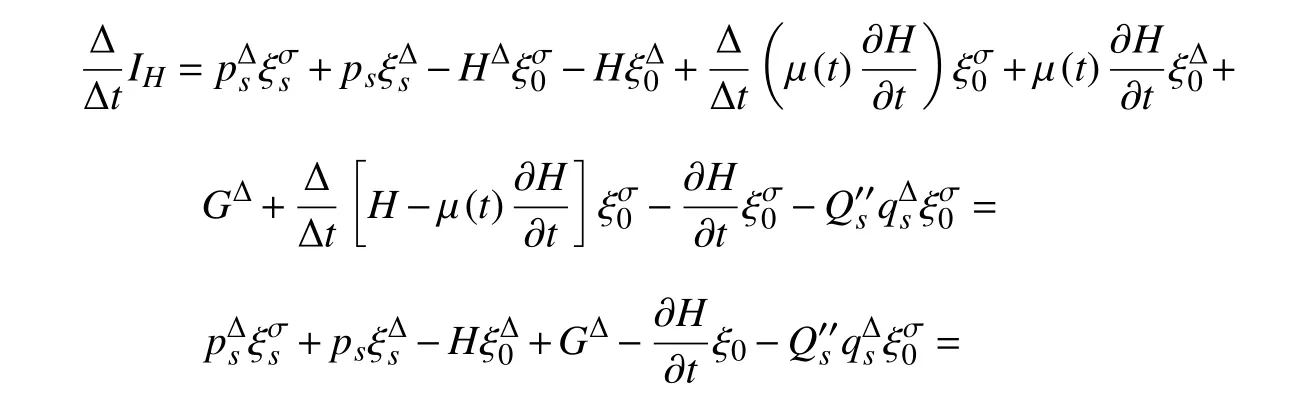
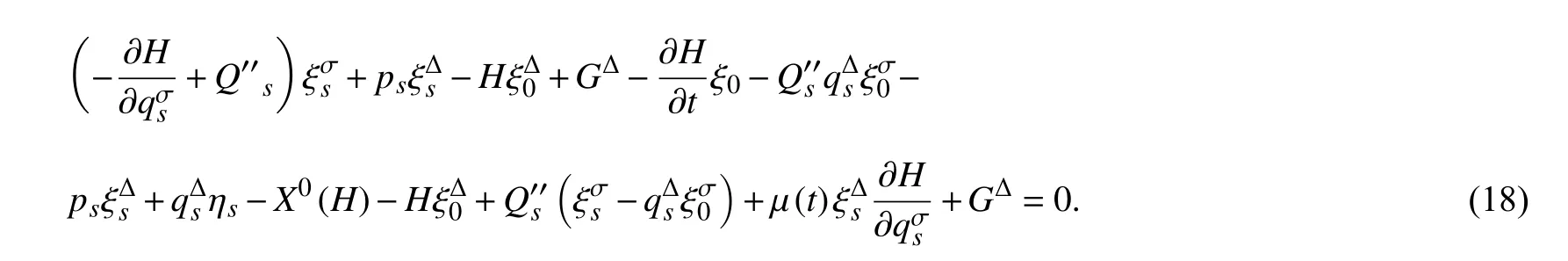
因此(17)式是该系统的守恒量.证毕.

3 Whittaker 方程在Birkhoff 系统下的Noether 定理

Hamilton 体系是Birkhoff 体系的一种特殊形式，若将时间尺度上Whittaker 方程力学化在Birkhoff 系统，相较于Hamilton 系统更具有普遍性，令

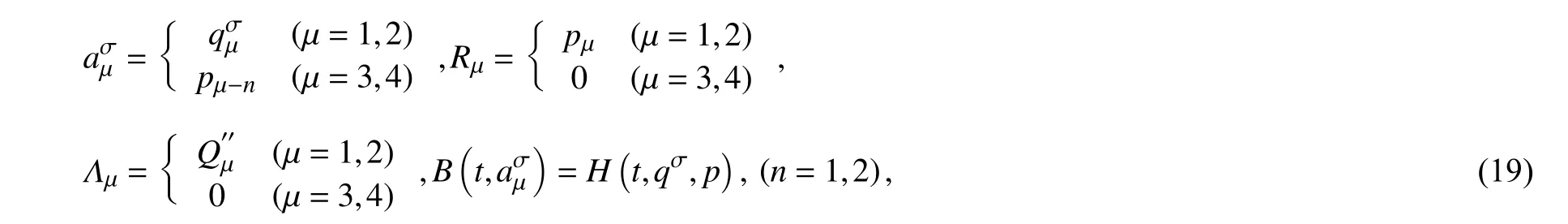
Whittaker 方程Hamilton 函数和广义力(11)式对应取得Birkhoff 函数和函数组、附加函数为

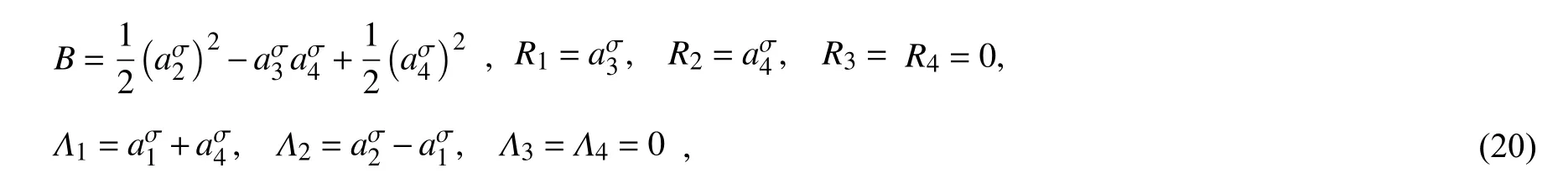
即Whittaker 方程在时间尺度上的Pfaff 作用量为

Whittaker 方程可以化为时间尺度上广义Birkhoff 方程，即

其中，ξ0,ξs是无限小变换的生成元.

定义3Pfaff 作用量在变换(23)下的不变性是时间尺度上Whittaker 方程相应于Birkhoff 系统下的Noether对称性.

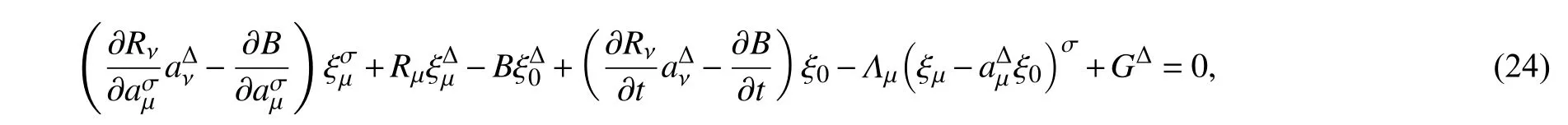
则此不变性是时间尺度上Whittaker 方程在Birkhoff 系统下的Noether 对称性.

定理3对于Whittaker 方程在Birkhoff 系统下，若变换(23)的生成元 ξ0,ξs使广义Noether 等式(24)成立，则此系统有Noether 守恒量

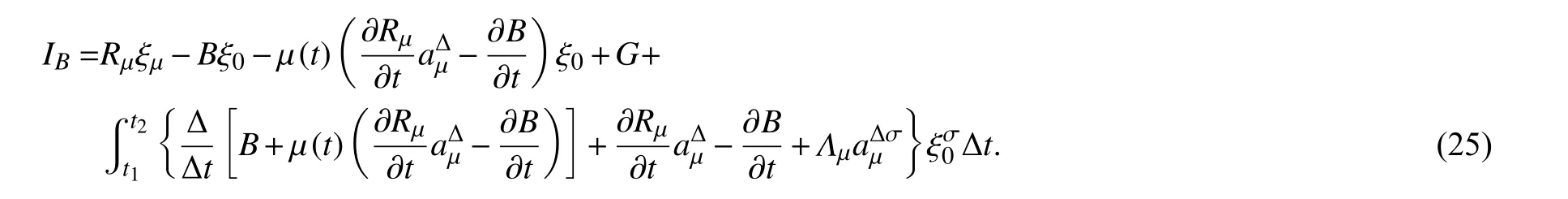
证明将式(25)两边对t求Δ-导数，并利用方程(22)和式(24)，可得

因此(26)式是该系统的守恒量.证毕.

若T=R，得σ(t)=t,μ(t)=0，则式(8)、(17)、(25)得到经典的Whittaker 方程在Lagrange、Hamilton、Birkhoff 系统下的Noether 守恒量依次为[19]

4 算例

例1时间尺度 T上Whittaker 方程可取Lagrange 函数和广义力为(2)式.

(2)式代入广义Noether 等式(6)，得到

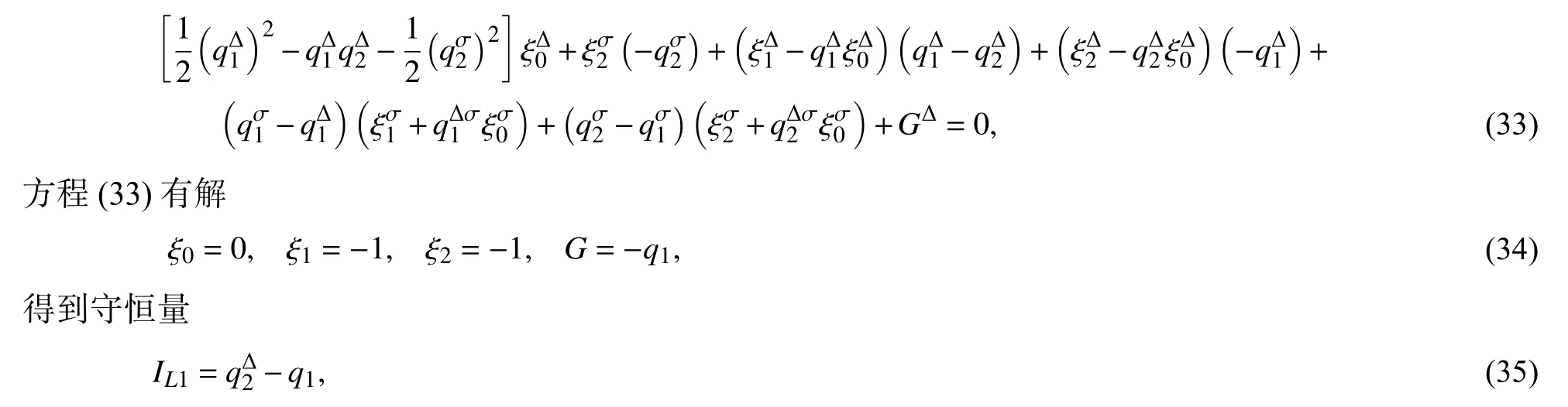
是生成元(34)运算出的Noether 守恒量.

时间尺度 T上 Whittaker 方程还可以取其他形式的Lagrange 函数为[19]

代入广义Noether 等式(6)，得到

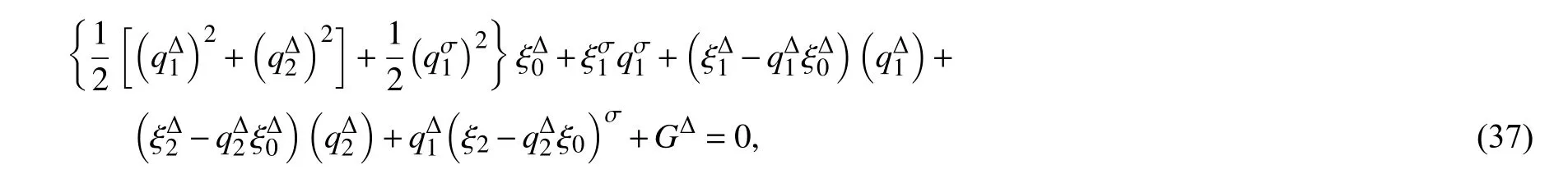
方程(37)有解

得到守恒量

是生成元(38)运算出的Noether 守恒量.

例2时间尺度 T上 Whittaker 方程的Lagrange 函数和广义力(2)式对应等价的Hamilton 函数和广义力为(11)式.

(11)式代入广义Noether 等式(15)得到

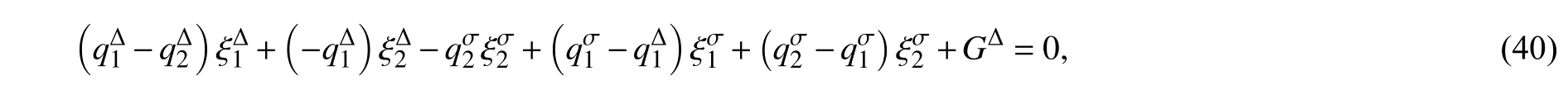
方程(40)有解

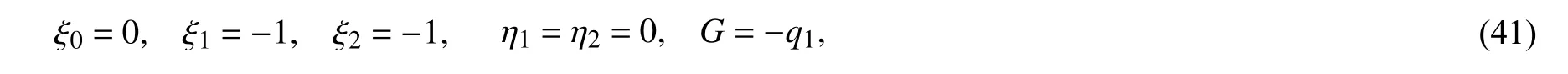
得到守恒量

是生成元(41)运算出的Noether 守恒量.

例3时间尺度 T上 Whittaker 方程Hamilton 函数和广义力(11)式对应取得Birkhoff 函数和函数组、附加函数为(20)式.

(20)式代入广义Noether 等式(24)得到

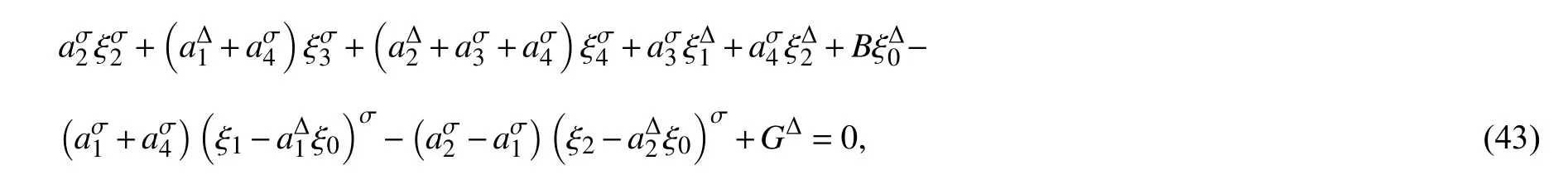
方程(43)有解

得到守恒量

是生成元(44)运算出的Noether 守恒量.

5 结论

本文研究了时间尺度上Whittaker 方程的Noether 守恒量，首先Whittaker 方程可力学化在一般完整的三大力学体系，由Noether 理论，得出Whittaker 方程的守恒量.其次由研究得出Whittaker 方程力学化时，其动力学函数在每个力学框架下选取可以有多个，结果可以找到相同的守恒量.Whittaker 方程在Lagrange 系统下得出的Noether 守恒量等价于Hamilton 系统下的，方程在Hamilton 系统下得出的Noether守恒量是Birkhoff 系统下的特殊形式，方程在Birkhoff 系统下更具有普适性.因此利用Noether 对称性求解时间尺度上Whittaker 方程的守恒量是一个变通性较强的方法.其思想方法可应用于研究微扰动力学方程等.