双变量不等式证明的多角度思考

钟国城

(广东省梅县东山中学，514017)

双变量不等式证明是高考数学的难点内容,往往以解答题中压轴题的形式出现.这类问题全面考查学生探究与解决问题的能力,重点考查学生的逻辑推理、数学运算等数学核心素养,以及化归与转化、分类讨论等重要数学思想.这类问题难度较大,求解方法多样,但解决问题的关键就是消元(换元),转化为单变量不等式进行求解.本文通过分析相关高考试题,总结此类问题的求解策略,以期对大家有所帮助.

角度1利用双变量之间的关系消元

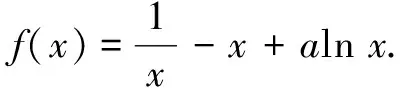
(1)讨论f(x)的单调性;

(2)若f(x)存在两个极值点x1,x2,证明:

解(1)略.

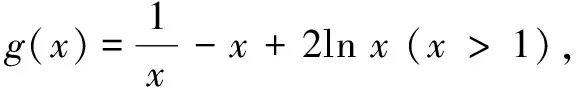
评注第(2)问由x1,x2是f′(x)的两个零点,得x1,x2为一元二次方程的根,故利用根与系数的关系得x1x2=1,为消元转化为单变量不等式的证明提供了便利,使问题顺利获解.

角度2利用双变量函数值之间的关系消元

例2(2016年全国高考题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围;

(2)设x1,x2是f(x)的两个零点,证明:x1+x2<2.

解(1)f′(x)=(x-1)(ex+2a).

当a=0时,f(x)=(x-2)ex只有一个零点,不合题意.

当a<0时,令f′(x)=0,得x1=1,x2=ln(-2a).

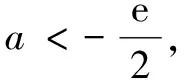
当a>0时,易见f(x)在(-∞,1)单调减,在(1,+∞)单调增.又f(1)=-e<0,f(2)=a>0,故f(x)在(1,+∞)有一个零点.

综上,a的取值范围是(0,+∞).

(2)不妨设x1f(2-x2).

又f(x1)=f(x2),所以f(x1)>f(2-x2)等价于f(x2)>f(2-x2),即f(x2)-f(2-x2)>0.

令g(x)=f(x)-f(2-x),x>1,则g′(x)=f′(x)+f′(2-x)=(x-1)(ex-e2-x)>0,g(x)在(1,+∞)单调增.又因为g(1)=0,故g(x)>0,可得f(x2)-f(2-x2)>0,从而x1+x2<2.

评注第(2)问是双变量不等式证明问题,首先将要证的式子转化为f(x1)>f(2-x2),再利用f(x1)=f(x2)转化为证明f(x2)>f(2-x2),即可达到消元转化为单变量不等式的证明,由此构造相应函数,降低问题的求解难度.

角度3对双变量整体换元

例3同例1.

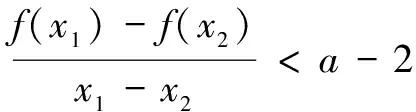
综上,得证.

角度4利用同构消元

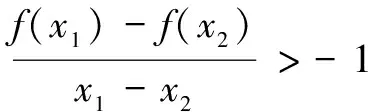
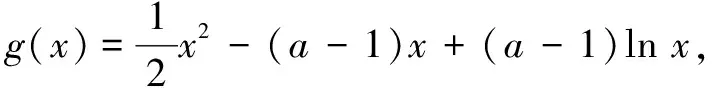
评注本题涉及双变量的同时,还带有另外的参数,看似求解困难,但将要证式子转化为f(x1)+x1

角度5利用主元法消元

例5(2020年天津高考题)已知函数f(x)=x3+klnx,f′(x)为f(x)的导函数.当k≥-3时,求证:对任意的x1,x2∈[1,+∞),且x1>x2,有

评注本解答视x1为自变量x,构造以x为主元的函数g(x),且注意到g(x2)=0,因此只需证明g(x)>g(x2).由此将双变量不等式转化为单变量不等式,问题的难点得以突破.