一道解析几何压轴题的分析与思考*

毛志伟 王 耀

(江苏省扬州大学数学科学学院,225002) (江苏省苏州市第一中学,215000)

一、试题呈现

(1)求椭圆C的标准方程;

(2)若直线MN的斜率k=1,求定点A的坐标.

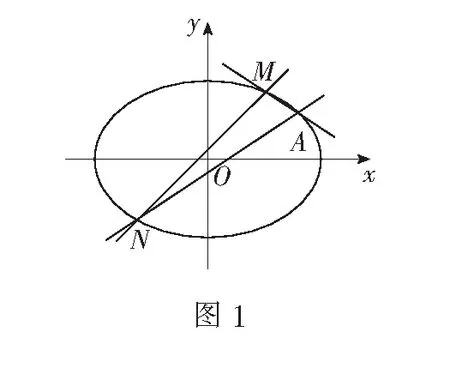
本题是2022年苏锡常镇四市高三一模解析几何压轴题.问题以斜率关系为背景,探究定点、定值问题,考查学生数学综合运用能力和数学运算素养.纵观近几年高考、模考试题,笔者认为此类问题具有一定的代表性,且解法灵活,具有一定的研究价值.因此笔者通过解法思考与优化、一般性结论探究及应用,多维度揭示问题本质,帮助学生积累经验,提升数学解题能力.

二、解法探究

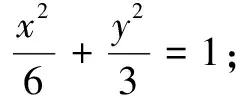
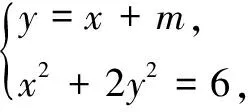
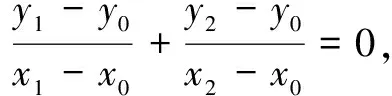
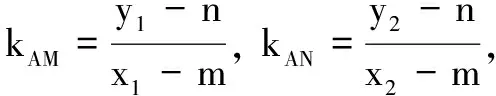
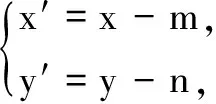
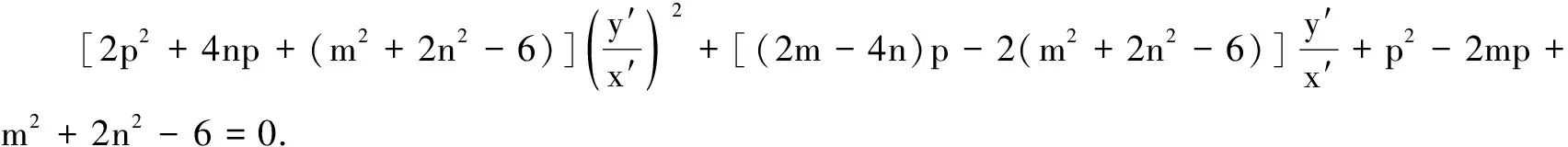
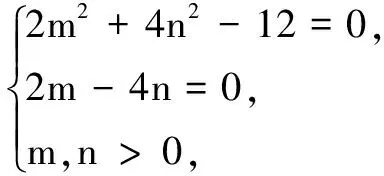
故点A的坐标为(2,1).

三、错解及反思

笔者发现部分同学审题不仔细,想当然地认为点A在椭圆上,利用直线AM,AN的斜率分别为k和-k,计算出点M,N的坐标,最终也能得到正确的结果.具体过程如下.

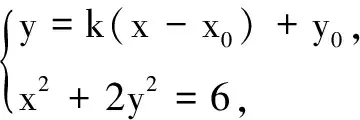
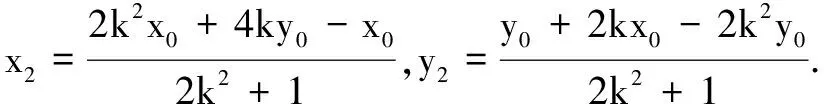
评注命题者在设计这道题时,也是精心构思的.从逻辑上看,该解法是不完整的,点A可以在椭圆上(如上述方法),也可能在椭圆外(利用上述解法是难以排除的).但祸兮福之所倚,通过该解法可发现如下一般的结论(证明见后面结论3).

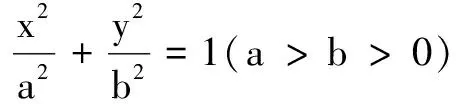
错解2设直线MN:y=x+m,点M(x1,y1),N(x2,y2).由kAM=-kAN,设直线AM:y=k(x-x1)+y1,直线AN:y=-k(x-x2)+y2.

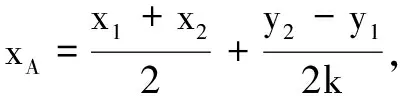
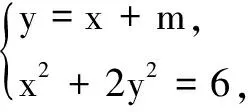
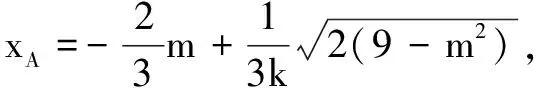
评注回看错解2,当m=-3时,判别式Δ=0,点M与N重合,即直线MN与椭圆相切,切点为(2,-1),斜率之和为0可看成正无穷与负无穷之和.该解法虽然存在问题,但此解法中也蕴含着如下结论.

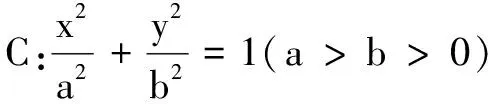
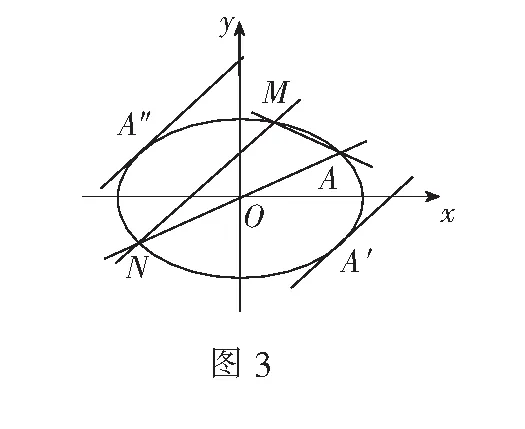
设点M(x1,y1),N(x2,y2),直线AM与AN的方程分别为y=k(x-x0)+y0,y=-k(x-x0)+y0.

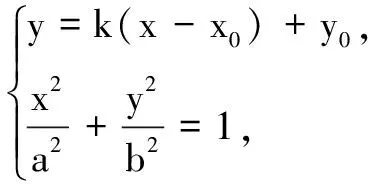
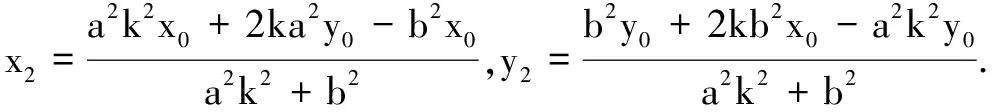
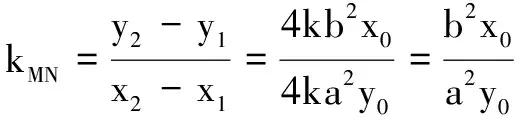
四、结论探究及应用

同前文利用齐次化方法探究点的坐标,也可以利用齐次化方法探究斜率关系,得到如下的一般化结论.

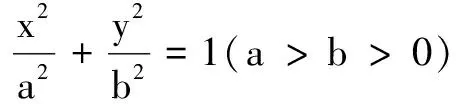
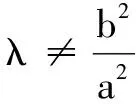
证明设点M(x1,y1),N(x2,y2).

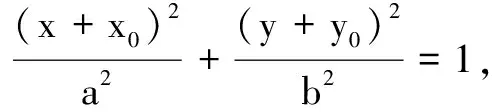
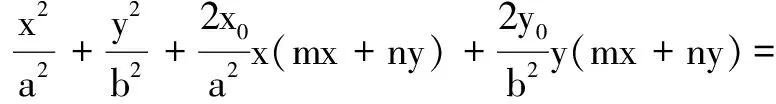
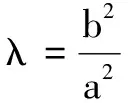
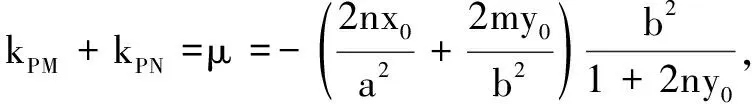
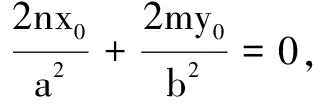
以斜率运算关系为背景的定点定值问题,在历年高考试卷和模拟测试卷中,也是屡见不鲜的经典问题,列举几道相关试题如下.

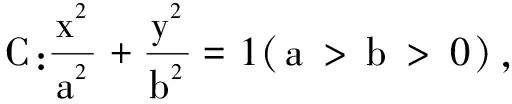
(1)求C的方程;

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与P2B的斜率和为-1,证明:l恒过定点.

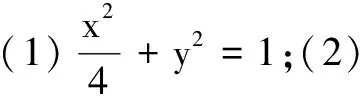
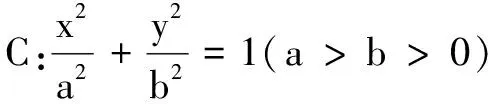
(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

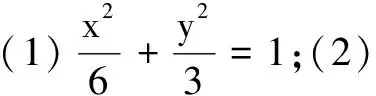
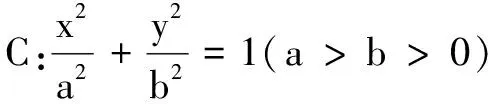
(1)求椭圆C的方程;

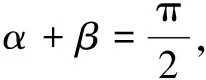
五、启示

波利亚在《怎样解题》一书中说:解题是一种实践性技能,可以通过模仿和实践来学会任何一种实践性技能.教学的重要任务之一就是帮助学生学会怎样解题.以文中研究的解析几何压轴题为例,首先要引导学生明白:已知条件是什么?求解的问题又是什么?在理解题意后,再去思考各个条件之间是如何关联的,并得到解题思路.

在问题解决的同时,本文还探究得到以斜率关系为背景的一些结论,可更好地帮助学生建立解决此类问题的知识结构,加深对问题的理解,在积累丰富的解题经验的基础上优化运算技能,以点带面,不断提升解题效率.