核心素养常培育 直观想象显魅力*——一道解析几何选择题的教学启示

陈建州 叶青柏

(福建省漳平第一中学,364400)

在解题教学中,特别是高三的复习教学中，不少师生常常一味追求解题技巧,忙于大题量的方法技巧训练,以此来提高数学解题能力,却忽视对数学本质的探讨与教学,忽视对数学核心素养的渗透、认知、感受和培育．这样做的效果往往是事倍功半，达不到预期的效果,也偏离对高考评价体系的认识与方向的把握．本文结合一道解析几何选择题的教学,探索核心素养之一直观想象核心素养在课堂教学中的渗透、培育,感受直观想象核心素养带来的数学教学魅力,提高学生对数学的学习热情与兴趣,落实新课程标准的要求．

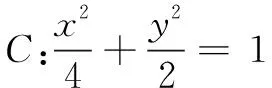
分析本题是一道圆锥曲线综合问题,考查直线与椭圆的位置关系、直线的斜率等．题目中涉及到的点和直线较多,解题时应根据题意准确画出椭圆的草图，找到相应的点和直线,从几何图形中直观捕捉到有用的信息，建立恰当的数学关系式求解．

一、基于直译已知与问题的求解

设P,Q两点坐标和直线PQ的方程,直接将几何元素转化成代数元素,用代数方法求解解析几何问题是常见思维和方法,逻辑思维严密,往往可形成严谨的推证求解过程，可作为解答题的通解通法．

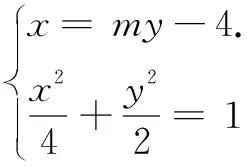
反思设点、设线、联立方程组是解析几何常见的解题套路,入手容易计算较难.在本题中，联立方程求两直线交点N的坐标就是一个难点,有较高的运算求解技巧要求,耗时较多,作为小题如此“大作”不划算!

二、基于取特殊点的求解

作为小题更多的应想到小题的做法,如取特殊点法等就是常用的方法．如在本题中让动直线经过特殊点即可在一定程度上实现问题的直观和具体化,让问题以图形的形式呈现出来,从而有助于思路的形成和计算量的减少．

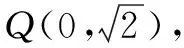
反思采用取特殊点、特殊值的方式，让复杂的解析几何问题直观化、具体化,让“动点”、“动直线”具体化、直观化为“定点”、“定直线”,便于作图和理解题意，便于利用具体的数值计算解决问题．实现“动”向“静”的转化,突破小题大做的大量字母参数的运算推理计算，大大简化计算．在一定程度上体现直观想象核心素养在解决相关问题上的价值与魅力．

三、基于数值、几何直观的求解

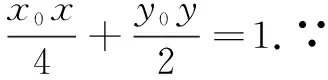
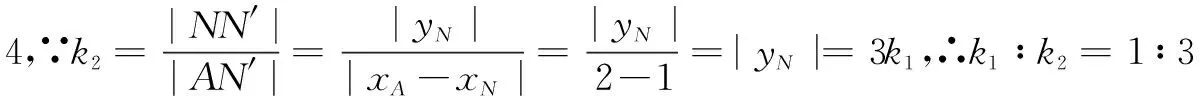
反思从几何图形中的点的运动变化过程直观想象到运动变化的极限情况,有效破解问题中运动变化的难点,实现“运动”向“静止”、“变”向“不变”的转化,达到多一点思考少一点计算的目标,节约答题的时间和精力，进一步体现直观想象核心素养在解题中的魅力．

四、基于直观想象核心素养下的探索与求解

利用直观认识几何图形信息或者利用直观想象让动直线运动起来,捕捉运动变化的极限位置,可以大大简化计算,实现“多思少算”的目标．如图5，重新读题、画图,不难发现符合题意的直线AP与BQ的交点N始终在Y轴的左侧,则可得到关键信息xN<0.

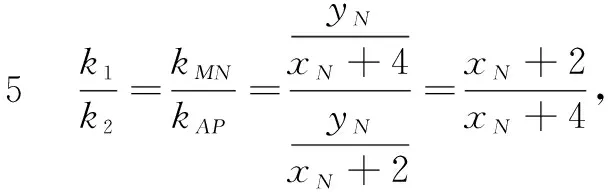
反思如此直观想象和感知题意、认识问题,彰显直观想象核心素养的魅力,在解题中实现“多思”几乎“不算”的小题解题方法．

数学核心素养的认知、渗透、培育并非一朝一夕之功,它的落地实施要求在课堂教学前充分挖掘教材、试题等素材，做好相关预设,在课堂教学中根据学生的具体课堂表现引导学生认知核心素养,感受核心素养带来的数学魅力．