HPM视角下数学学科核心素养的生成与教学实践研究*
——以人教A版“数学归纳法”教学为例
2022-11-28蒋松言沈中宇
蒋松言 高 翔 沈中宇
(1.南京信息工程大学教师教育学院,210044;2.苏州大学数学科学学院,215006)
数学史与数学教育(HPM)是一个重要的学术领域,数学学科核心素养是新一轮课改中的重点概念,也是学者们研究的热点问题.本文探讨HPM视角下数学学科核心素养的生成,并以“数学归纳法”的教学为例,将生成机制运用到教学实践中.
一、HPM视角下数学学科核心素养的生成机制
《普通高中数学课程标准(2017年版)》[1](以下简称《课标》)颁布后,许多学者研究了数学学科核心素养的生成问题.王尚志从教师、学生、课程、评价四个角度进行分析,给出了数学学科核心素养的生成方法[2];吕世虎将数学学科核心素养的体系划分为数学双基层、问题解决层、数学思维层、数学精神层[3];朱立明则将数学学科核心素养的结构分为数学知识、问题解决、数学思维三个层次,并阐述了不同教学内容有效组织协同、各层次教学活动共同作用、核心素养各成分相互凝聚而带来的数学学科核心素养整体提升的过程[4].
本文基于朱立明的数学学科核心素养基本结构三层次:数学知识、问题解决、数学思维,结合汪晓勤提出的数学史融入数学教学的运用方式:附加式、复制式、顺应式、重构式,尝试构建HPM视角下数学学科核心素养的生成机制(如图1所示)[5].其中数学史素材的运用方式与数学学科核心素养的基本结构关系如表1所示.
综上,数学史是沟通数学教学与数学学科核心素养的桥梁,通过数学史素材的合理运用,可以为教学实践中数学知识、问题解决的教学,乃至数学思维的培养提供丰富的素材,进而达成培养数学学科核心素养的目的.
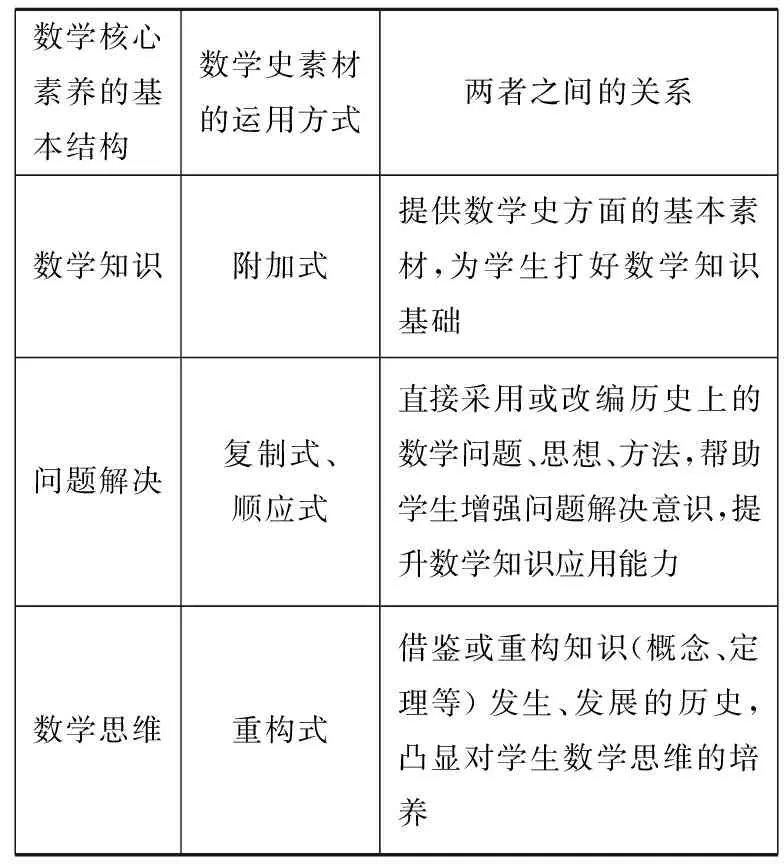
表1数学史素材运用方式与核心素养结构的关系
二、HPM视角下数学学科核心素养的教学实践示例
本文以“数学归纳法”的教学为例,对比传统教学和融入HPM的教学设计,尝试将HPM视角下数学学科核心素养的生成机制运用于教学实践.
1.教材分析
和以往教材不同,人教A版(2019年版)将“数学归纳法”调整到选择性必修二“数列”部分的最后一节进行教学,更加强调“数列”与“数学归纳法”之间的联系.实际上,数学归纳法是用于与正整数相关命题的证明,和数列关系密切;同时,递推是数列的本质属性,亦是数学归纳法的核心思想[6],故在实际教学中需要对数列的递推公式进行适当回顾后再展开数学归纳法的教学.人教A版教材从一道证明题入手,引导学生思考在已知递推公式的情况下猜想通项公式并证明,在学生认识到逐项证明极其繁琐后引出数学归纳法.通过类比多米诺骨牌倒塌的特点,向学生传递数学归纳法的基本思想,并基于此思想解决本节课开始的证明题.最后正式给出形式化的数学归纳法,并引导学生应用其证明简单命题.
2.通常的教学过程
本文根据文章[7]与[8]归纳总结出常见的数学归纳法教学设计,内容如下:

情境2观看多米诺骨牌倒塌的视频,观察总结其倒塌的两个特点.
活动1根据情境2的特点,类比多米诺骨牌和数列通项,完成下列表2.

表2
活动2思考如何证明情境1中所给出的问题.
活动3阅读教材内容,请同学回答问题:什么是数学归纳法?教师讲授数学归纳法的概念及基本原理.
活动4请同学练习使用数学归纳法证明:2+4+6…+2n=n2+n.
教学设计分析这样的教学设计较好地覆盖数学归纳法的几个基本要素,但仍有两方面的问题值得深入探讨:一是直接举出多米诺骨牌倒塌的例子并让学生总结特点,初学者往往不能抓住多米诺骨牌倒塌和数学归纳法的相似特点,容易导致实际教学效果偏于设计;二是缺少对于“P(k)到P(k+1)”中k值的任意性的解释,可能误导学生认为数学归纳法只能使用在解决有限项的命题上[9].从HPM视角下数学学科核心素养生成机制的角度看,此设计中数学史素材的运用往往停留在以附加式、复制式为主的方式上,数学学科核心素养的结构层次也往往停留在数学知识和问题解决层面上,难以上升到数学思维层面,仍有进一步提升的空间.
3.基于HPM的教学过程
教学过程融合“数学知识——问题解决——数学思维”的数学学科核心素养生成机制,设计了三个情境用于传授数学知识,解决示例问题,并在帮助学生深入理解数学归纳法思想的同时,培养学生观察发现、演绎证明等数学思维,逐步培养学生数学抽象、逻辑推理等数学学科核心素养.
具体教学设计如下:
情境1毕达哥拉斯学派用小石子排列成不同形状来研究数,例如三角形数和正方形数(如图2所示).其中正方形数每一层石子的个数依次排列可以得出奇数数列:1,3,5….
(1)求正方形数前n层石子总数Sn,即求数列前n项和.
(2)写出Sn和Sn-1的关系式,即写出数列{Sn}的递推公式.
设计意图情境1利用复制式引导学生了解三角形数和正方形数的背景,同时复习数列递推的相关数学知识,为情境2,3利用这一数学史素材开展教学奠定基础.
情境2同学们用求和公式可以轻松回答情境1问题(1),可早在毕达哥拉斯时代还不存在求和公式,但发现了1=12,1+3=22…,由此猜想Sn=n2.那该如何证明呢?请依次思考下列问题:
(1)怎么利用等式S1=1=12和递推公式Sn=Sn-1+2n-1得出等式S2=1+3=22?
(2)怎么利用Sn-1=(n-1)2和递推公式证明Sn=n2?
(3)我们知道1=12是成立的,问题(2)也可以达成,能否说明Sn=n2对所有的n都成立?
最后引出数学归纳法的概念.
设计意图数学归纳法的发展经历了四个阶段:萌芽阶段利用形数、递推进行猜想;发展阶段由证明有限项命题转为证明无限项命题;成熟阶段诞生了数学归纳法现代意义上的两个核心步骤;形式化阶段则是给出数学归纳法概念的现代形式.情境2中的猜想与三个问题重构了前三个历史环节(如图3所示),进而展开数学归纳法概念的教学.
情境2运用重构式,通过正方形数得到猜想,带领学生经历数学归纳法的历史“萌芽阶段”,再引导学生从具体情况入手,问题(1)让学生认识到可以用n=1时的等式及递推公式推出n=2时的等式,感受“发展阶段”中有限项命题的证明;问题(2)引导学生观察前一步可以推出后一步的现象以及n值的任意性,体验“发展阶段”中无限项命题的证明;问题(3)则引导学生认识数学归纳法的两个核心步骤.情境2中设计的三个小问题引领学生回溯数学归纳法历史发展的各个阶段,引导学生初步认识第一数学归纳法.这样的设计既解决以往教学设计中学生无法将多米诺骨牌倒塌特点和数学归纳法之间建立联系的问题,又帮助学生深刻认识“P(k)到P(k+1)”k值任意性解释的问题.在问题解决的情境中激发学生的学习动机,促进学生对数学知识的理解,逐步培养学生观察发现、演绎证明的数学思维.
情境3讲授数学归纳法的两个基本步骤(奠基、归纳递推),引导学生观察三角形数,利用补成“四边形数”的方法(如图4所示)猜想三角形数前n层石子总数,并利用数学归纳法证明.
设计意图《课标》要求学生“了解数学归纳法的原理,能用数学归纳法证明数列问题中的一些简单命题”.情境3的设计一方面帮助学生理解数学归纳法的两个基本步骤,另一方面利用顺应式创设用数学归纳法证明数列中简单命题的问题情境,帮助学生应用新知初步解决与数学归纳法相关的问题.
从《课标》要求的角度看,三个情境完成了《课标》对于数学归纳法教学的基本要求,并引导学生思考数学归纳法的基本思想,增强学生对数学归纳法的认识;从重点、难点角度看,情境1和情境3分别完成教学重点中对数学归纳法的发现和应用,情境2则突破理解数学归纳法思想这一教学难点;从HPM视角下数学学科核心素养生成机制的角度看,此设计以数学史素材为桥梁,达成数学归纳法中数学知识和问题解决的教学,突出观察发现、演绎证明等数学思维的培育,从而逐步达成培养学生数学抽象、逻辑推理等数学学科核心素养的最终目的.
