LabVIEW一阶系统虚拟教学实验系统开发

鹿 尧

（南京理工大学机械工程学院，南京 210094）

0 引言

随着虚拟仪技术的发展，基于虚拟仪器的虚拟教学系统的开发也随之得到社会的关注。虚拟仪器是通过一些软件平台可以把电脑与一些程序模块整合，操作者可以通过这些软件平台和程序模块自主定义、设计虚拟实验[1]。虚拟仪器之所以会发展如此迅速，与传统仪器提供了强大的理论支持和操作基础密不可分。表1所示为两者之间的比较。

表1 两种仪器的对比

下面举出几个国外的虚拟仪器的例子：如美国国防部高级研究与发展计划联合开发了虚拟仿真互联网平台系统VINT[2]；由美国俄勒冈大学物理系主办的物理实验网站VLAB[3]；美国巴尔的摩一个基于Java技术的虚拟物理实验室项目[4]；德国鲁尔大学开发的VClab实验室[5]；由新加坡国立大学电子工程系开发的工程教育虚拟实验室[6]。

尽管中国对虚拟仪器的研究起步较晚，但是这些年里也是有所发展。如中国科技大学研制出了几何光学设计平台的物理虚拟实验室[7]；北京大学计算机系设计开发的流水线实验和CACHE实验两套网络虚拟实验室[8]；华中科技大学开发了液压回路性能和液压元件装拆虚拟实验[9]；北京师范大学现代教育技术研究研制了一个基于虚拟空间的三维电子线路实验环境的Evlab系统[10]。此外，虚拟仪器如口腔实验教学[11]、细胞遗传学实验[12]等医学应用方面也有很大的进步；并且在管理学方面也有所发展，如区块链+电子商务虚拟实验[13]等方面的研究。

本文基于虚拟仪器软件——LabVIEW对一阶惯性系统进行网上虚拟实验的搭建。一方面完成了一套一阶惯性系统的仿真和PID控制实验，有助于缓解现实中的实验教学资源分布不均衡，可以降低实验室所属的相关单位的财务开销，使得使用者对一阶惯性系统和PID控制了解更加简单，方便和易懂；另一方面针对一阶惯性系统的PID控制，利用本次搭建的实验系统中经过PID控制后得到的系统时域响应图，通过更改PID控制中的变量参数，对比不同变量产生的时域响应图最终可以得出PID控制中积分单元、微分单元和增益单元对系统的影响[14-15]。

1 一阶系统虚拟教学实验的基础理论

1.1 一阶系统概述

则可以得出其幅频特性为：

对于一阶惯性系统的波德图的计算，以式（2）为例，其对数幅频特性为，对数相频特性为φ(w)=-arctanwT。

在LabVIEW上模拟出当净增益K=1，时间常数时的结果如图1所示。

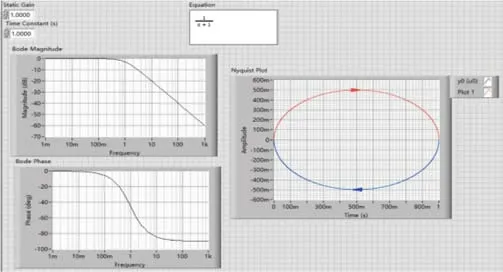
图1 典型一阶惯性系统频率特性

1.2 一阶系统的单位阶跃响应

当阶跃信号作为系统的输入信号时，首先阶跃信号其数学表达式可以表示为经过拉普拉斯变换之后的拉氏变换式为R(s)=，则上述系统的该时间响应的拉氏变换式为：

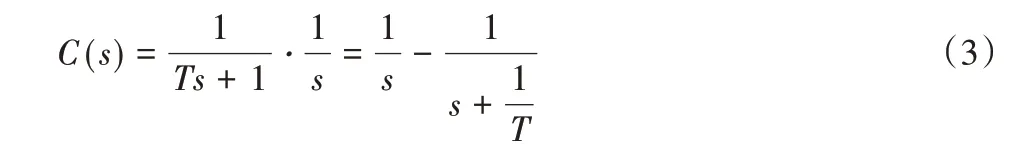
再将式（3）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW模拟出来的一阶惯性系统的单位阶跃响应前面板如图2所示。

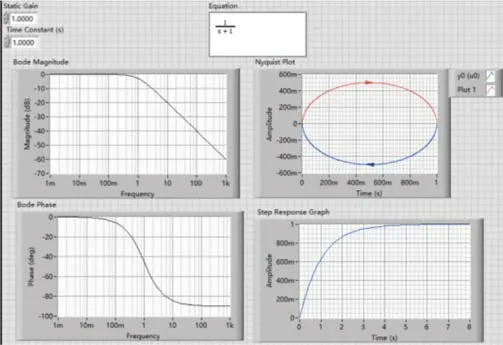
图2 一阶系统单位阶跃响应

简单介绍该曲线的相关特性。由式（3）可以计算出时间响应曲线的初始斜率：

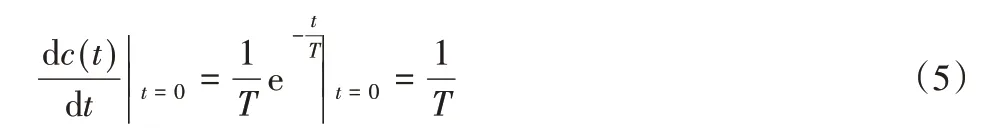
式（5）有利于计算出该一阶惯性系统的时间常数，对于图2中的一阶惯性系统的时间常数即为1。

该一阶惯性系统阶跃响应曲线最终趋于一定值的曲线，并且该系统并不具备振荡特征。因此该系统的时间响应并没有超调量。

最后，也可以直接从图2看出，当t→+∞时，系统的稳态误差

1.3 一阶系统的单位脉冲响应

当脉冲信号作为系统的输入信号时，首先脉冲信号其数学表达式可以表示为，经过拉普拉斯变换之后的拉氏变换式为R(s)=1，则上述系统的该时间响应的拉氏变换式为：

再将式（6）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW模拟出来的一阶惯性系统的单位脉冲响应前面板如图3所示。

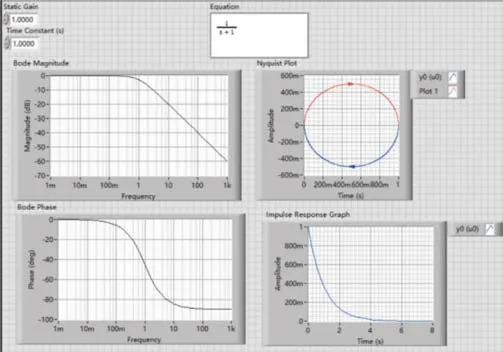
图3 一阶系统单位脉冲响应

对于一阶系统的单位脉冲响应信号曲线，当时间t逐渐增加，直至当t→+∞时，c(t)=0。因此一阶系统的单位脉冲响应无稳态分量。计算该时间响应曲线的初始斜率

2 虚拟教学实验设计

LabVIEW中有两种PID控制器的控件，一种是测量测试使用的PID控件，另一种就是此次设计所需要的控制设计与仿真模块的PID控件。

PID控制也叫比例积分微分控制，它兼具比例微分控制的改善系统动态品质和比例积分控制的：

式中：Kp为比例单元增益系数；Ti为积分单元的系数；Td为微分单元的系数。

在PID控制中各个单元的作用也有不同，具体如下。

（1）比例单元通俗地说就是一个起到放大作用的单元，比例单元的系数越大，放大的倍数也就越大，但是被控制、被调节的参数的曲线波动也越大。系统在比例单元运作时也会因为比例单元放大的时候会产生与实际被测参数产生偏差，这时候就需要引入积分单元进行工作。

（2）积分单元的作用就是当系统产生偏差时，积分单元就会随着时间进行积累，逐渐抵消这个偏差，只要偏差一直存在，积分单元将会一直运行。

（3）微分单元的作用就是解决被控对象的滞后问题。

一阶系统PID控制实验设计如下。

对一阶系统先进行PID控制再进行时间响应。前面内容已经介绍了一阶系统的传递函数而PID控制的传递函数将两个传递函数相乘得出整个系统的传递函数为：

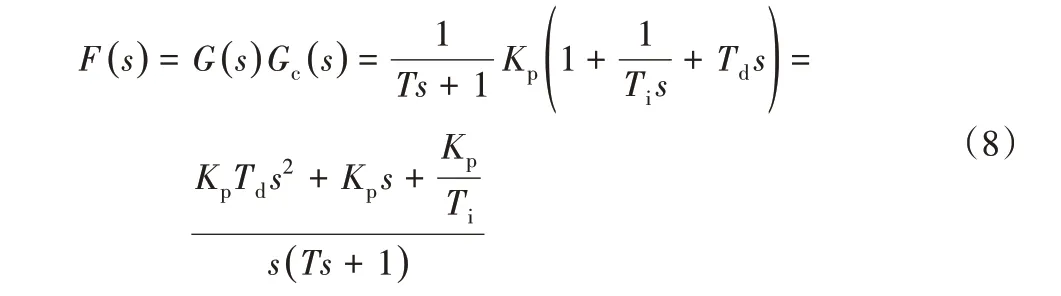
下面通过几个示例进行对比，来观察整个系统的时间响应有什么区别。

对于同一个一阶系统，假设其时间常数为1，净增益也为1，那么这个一阶系统的传递函数就为G(s)=。对于这样一个一阶系统，每次只改变PID控制中3个参数其中一个，再给予这整个系统一个相同的时间响应，观察最终的响应信号的时域图。

2.1 整个系统的单位阶跃响应

先取PID控制环节的3个参数：比例系数为20，积分系数为0，微分系数为0.01，得出PID控制环节传递函数为Gc(s)=0.2s+20，那么整个系统的传递函数即为F(s)=。当整个系统的时间响应为单位阶跃响应，其拉普拉斯变换式为R(s)=1s时，则上述系统的该时间响应的拉氏变换式为C(s)=再将C（s）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图4所示。

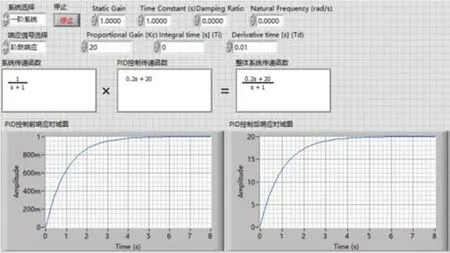
图4 整体系统的单位阶跃响应时域图

当只改变PID控制环节中的一个参数，保持另外两个参数不变再进行处理。先改变比例系数，不改变微分系数和积分系数，使比例系数由20变为40。于是PID控制环节的传递函数就变为Gc(s)=0.4s+40，整体系统的传递函数为F(s)=当相同的单位阶跃响应作用在这个系统上时可以得出输出的拉氏变换式为，再对C（s）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为

用LabVIEW对上面的计算环节进行模拟，如图5所示。

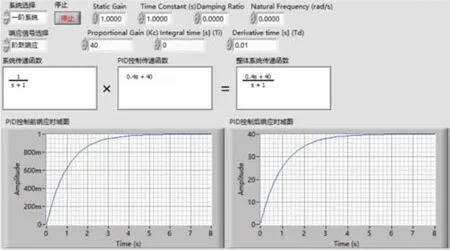
图5 Kp=40时整体系统的单位阶跃响应时域图

再保持原来的比例系数20不变，只改变积分系数，不改变微分系数，把积分系数由原来的0改为0.1。于是PID控制环节的传递函数就变为，整体系统的传递函数为，当相同的单位阶跃响应作用在这个系统上时可以得出输出的拉氏变换式为C(s)=，再对C（s）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图6所示，发现该时域图发散。

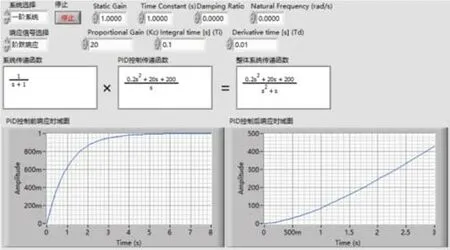
图6 Ti=0.1时整体系统的单位阶跃响应时域图

再保持原来的比例系数和积分系数不变，只改变微分系数，使微分系数由0.01变为0.2。于是PID控制环节的传递函数就变为Gc(s)=4s+20，整体系统的传递函数为F(s)=，当相同的单位阶跃响应作用在这个系统上时可以得出输出的拉氏变换式为再对C（s）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图7所示。

图7 Td=0.2时整体系统的单位阶跃响应时域图

2.2 整个系统的单位脉冲响应

对于相同的PID控制环节，其传递函数为Gc(s)=那么整个系统的传递函数即为F(s)=当整个系统的时间响应为单位脉冲响应，其拉普拉斯变换式为R()s=1时，可以得出整个系统的输出的拉氏变换式为再对C（s）经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图8所示。

图8 整体系统的单位脉冲响应时域图

当只改变PID控制环节中的一个参数，保持另外两个参数不变再进行处理。先改变比例系数，不改变微分系数和积分系数，使比例系数由20变为40。于是PID控制环节的传递函数就变为整体系统的传递函数为，当相同的单位脉冲响应作用在这个系统上时可以得出输出的拉氏变换式为C(s)=，再对C(s)经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图9所示。

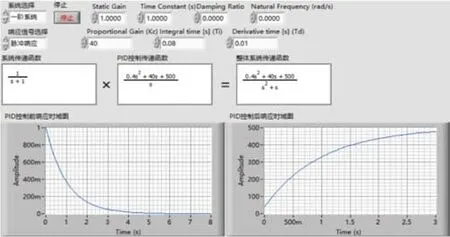
图9 Kp=40时整体系统的单位脉冲响应时域图

再保持原来的比例系数20不变，只改变积分系数，不改变微分系数，把积分系数由原来的0.08改为0.16。于是PID控制环节的传递函数就变为整体系统的传递函数为，当相同的单位脉冲响应作用在这个系统上时可以得出输出的拉氏变换式为C(s)=，再对C(s)经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图10所示。

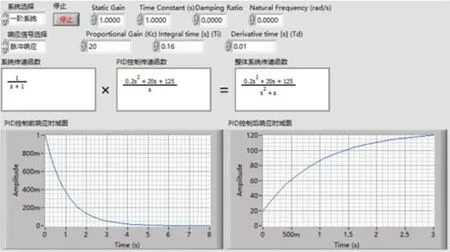
图10 Ti=0.16时整体系统的单位脉冲响应时域图

再保持原来的比例系数和积分系数不变，只改变微分系数，使微分系数由0.01变为0.2。于是PID控制环节的传递函数就变为，整体系统的传递函数为，当相同的单位脉冲响应作用在这个系统上时可以得出输出的拉氏变换式为再对C(s)经过拉普拉斯反变换转化成数学表达式。得到输出的原函数为：

用LabVIEW对上面的计算环节进行模拟，如图11所示。

图11 Td=0.2时整体系统的单位脉冲响应时域图

3 结束语

本文利用LabVIEW设计了一款一阶惯性系统的相关特性和PID控制下一阶惯性系统的时域图，可以完成对于一阶惯性系统的部分控制实验，完全开发达到使用者直接通过对实验系统前面版相关系数的更改来获得所希望的一阶惯性系统和PID控制效果的要求。

同时根据仿真数据可以直接得出对于相同的时间响应信号，PID控制环节的参数的改变对于其输出的时域图的影响可以总结得出：（1）当积分系数和微分系数相同时，比例系数越大，时间响应曲线在稳定前的增加速率越大；（2）当比例系数和微分系数相同时，积分环节系数越大，时间响应曲线在稳定前的增长速率减小；（3）当比例系数和积分系数相同时，微分系数对于整个系统的影响较小。