海上风电安装船桩腿风浪流耦合有限元对比分析研究*

林超辉，曾镜灵，赖柏豪，吴平平，梁岩峰，姜季江，张永康※

（1.广东工业大学机电工程学院，广州 510006；2.广东精铟海洋工程股份有限公司，广东佛山 528241；3.启东中远海运海洋工程有限公司，江苏启东 226251；4.中远海运重工有限公司，上海 200135）

0 引言

桩腿是自升自航式海上风电安装船的关键部件，保障了风电安装船在风大浪急的复杂海洋条件中有一个平稳的安装环境，对风电安装船的稳定性起着重要的作用[1]。海上风电安装船在作业时，桩靴插入海底泥土中，为整个船体提供承载力，此时桩靴和土层产生相互作用。因此，考虑桩土相互作用，分析风电安装船的稳定性是必要的。

国内外学者对桩腿的分析做了大量研究，Yuguang Cao等[2]基于ANSYS，建立了桁架腿顶升的三维模型，考虑到流体－结构－土壤的相互作用，对模型进行了静态分析。张永康等[3]建立了圆壳形桩腿的铰支模型和桩土相互作用模型，并对两种底部约束模型进行了静态分析，结果表明，铰支模型和桩土相互作用模型计算值有差异，铰支约束的弯矩曲线在桩端约束处出现了突变峰值，而桩土相互作用约束下的弯矩变化较为缓和。杨怡飞[4]建立自升式平台桩腿模型，分析了桩腿在不同类型土体中的受力特性，研究了桩土参数对桩腿水平承载力的影响，并与API规范p-y曲线进行了对比。结果表明：土体弹性模量的增大使桩身位移从0.45 m减小到0.34 m；粘聚力增大使桩身位移减小超过了50%。综上所述，在进行桩腿有限元分析时，考虑桩土的相互作用是必要的，但目前国内外尚未有对大规模风机安装的风电安装船桩腿结构进行数学建模、静态分析的相关文献。因此，本文以风电安装船的桩腿作为研究对象，分别建立了不同约束下的桩腿有限元模型：刚性固定模型和桩土耦合模型，从静态分析方面对桩腿进行数值模拟，并进行比较研究。

1 模型建立

整船结构主要采用SESAM软件进行建模，SESAM是一款由挪威船级社（DNV）开发，具有50多年悠久历史，船舶与海洋工程领域得到广泛认可和应用的软件工具系统。可广泛应用于海洋固定式结构的设计和分析，无论是浮式系统的上部结构、导管架平台、自升式平台还是海上风力发电机的基础结构等，SESAM在其整个结构的服役周期中都可以为关键的工程决策提供分析及数据支持。

安装船船体采用板单元建立，桩腿采用杆单元建立。在有限元模型中，杆单元通过节点与板单元相连，从而传递载荷。由于本研究的对象为桩腿，故船体内部结构忽略不计，仅考虑船体重力和船体风载对桩腿的影响。因此在有限元模型中，船体仅采用板单元建立，舱壁均匀分布在整个船体长度方向上，用修改材料密度的方法使得船体整体重量与设计值一致，船体如图1所示。由于船体相对桩腿刚度较大，暂不考虑船体刚度对桩腿的影响。在设计过程中，船体与桩腿连接处会采用加强结构，避免船体结构破坏。数值模型中，在桩腿处增加舱壁模拟加强结构。由于SESAM软件在进行桩土耦合分析中，必须考虑圆管截面进行桩基础的模拟。根据船体总布置图，桩靴宽度为11.6 m，在桩靴模型建立时设定圆管截面直径保持与桩靴宽度一致，为11.6 m。整船模型（含桩腿）如图2所示。

图1 船体模型

图2 整船等效模型

根据风电安装船在作业时桩腿底部和土层的约束条件，建立刚性固定模型和桩土耦合模型。刚性固定模型中，省略桩靴结构，桩腿结构与海底泥面直接刚性固定，该固定截面限制6个自由度，刚性固定模型效果如图3所示。

图3 刚性固定模型

桩靴在海底土层下受力有：桩侧土体法向抗力、桩侧土体轴向抗力、桩端土体轴向抗力。由于海底地质条件未知，桩土作用力采用API RP 2A-WSD[5]规范推荐的工况来计算，取硬质土厚度为5 m，软质土厚度为20 m，土质条件如表1所示[6]。

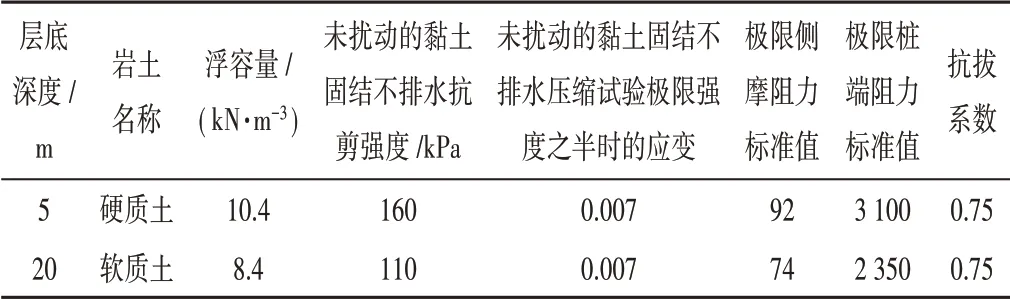
表1 桩土耦合土质条件

用P-Y曲线弹簧模拟桩侧土体法向抗力，用T-Z曲线弹簧模拟桩侧土体轴向抗力，用Q-Z曲线弹簧模拟桩端土体轴向抗力，如图4所示[6]。建立的桩土耦合有限元模型效果如图5所示。

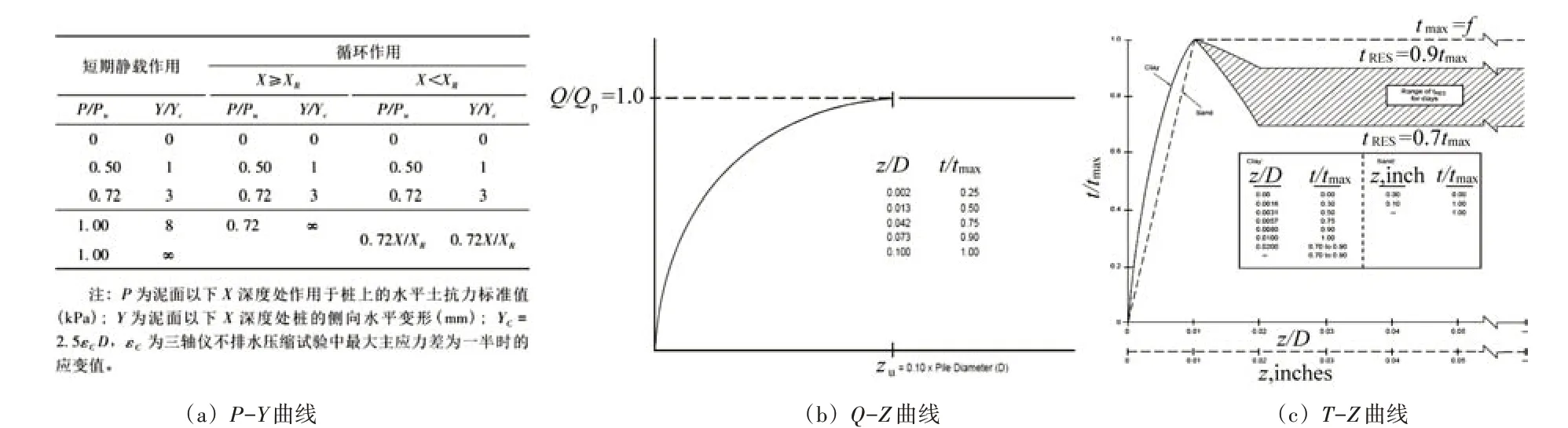
图4 桩土耦合数学模型

图5 桩土耦合有限元模型

2 载荷计算及加载

风载荷、波浪载荷和海流载荷是自升自航式风电安装船在站立状态下承受的主要载荷，根据挪威船级社（DNV）规范DNV-RP-C104中的规定进行计算。

2.1 风载荷

平均风速的大小与标准时距的取值是密切相关的，DNV规范取1 min为平均风速的标准时距。通常情况下假设风、浪、流3种载荷同向。自升式平台（船）的风速计算如式（1）所示，是一个以计算高度距离静水的距离为自变量的函数[7]。

式中：vR为参考高度为10 m、时距为1 min时的风速，m/s；z为风速计算点距离静水的高度，m；z0为参考高度，z0=10 m；n为状态系数，当平台为自升状态时，n=11，当平台为迁航状态时，n=14。

平均风时恒定风速下的海面以上结构受力，可视为静力，风速越大，对结构的压力越大，计算公式如下[8]：

式中：ρ为空气密度，kg/m3，干燥空气取ρ=1.225 kg/m3；A为受风面在垂直风向上的投影面积，m2；v为根据式（1）计算得到的设计风速，m/s；CS为形状系数，如表2所示。

表2 形状系数[8]

为保守估计，作用在船体和桩腿的形状系数都取值1.5，且暂不考虑桩腿相互之间的屏蔽效应。

风载荷以面压力加载在船体上，以线载荷加载在桩腿上。在风暴自存工况和正常工作工况下，桩腿和船体的风载荷如表3所示。

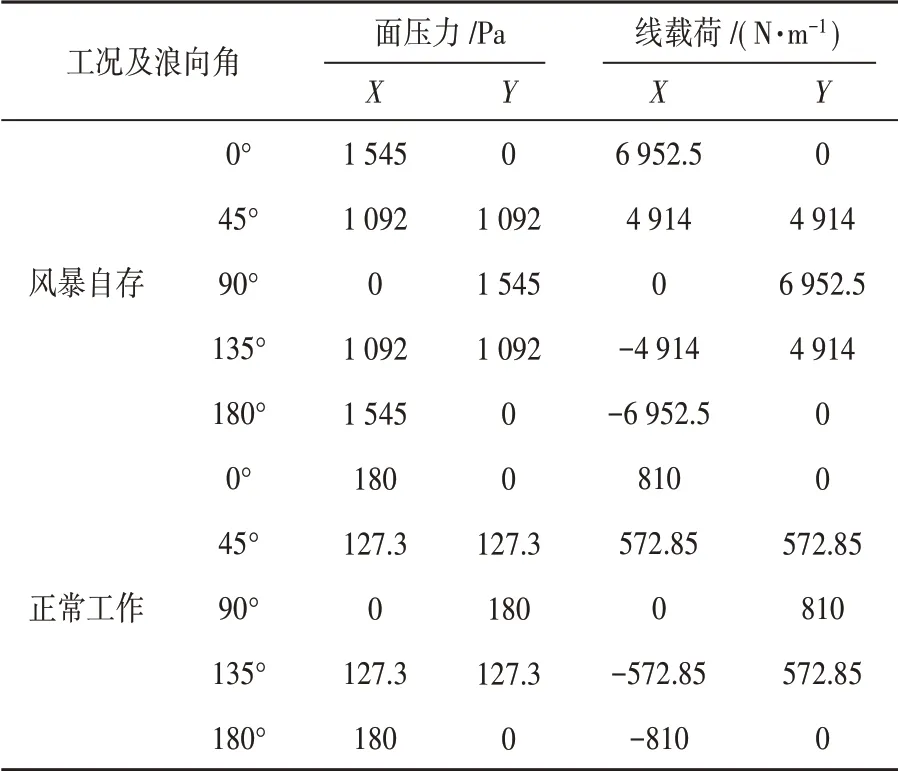
表3 不同工况下风载荷

2.2 波浪载荷

选用Stokes五阶波理论分析波浪[9-10]，如式（3）～（5）所示。

波面公式：

波长公式：

速度势：

式中：d为水深；H为波高；T为波浪周期；L0为深水波长；k为波数；θ为相位角；λ为比值系数；Bij、Ci为系数；ηi为波形系数；φi为速度势系数。

取风暴自存工况下的波高为15 m，波浪周期为14 s，正常工作工况下的波高为4.8 m，波浪周期为8 s。

桩腿的波浪载荷和流载荷采用Morison[11-12]公式进行计算，波浪载荷可分为拖曳力和惯性力两个分量，计算公式如下[13]：

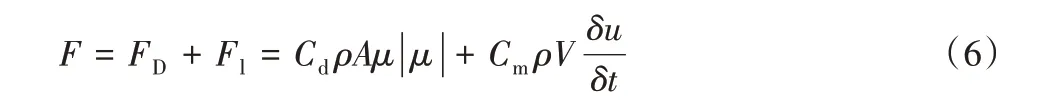
式中：F为垂直作用于构件轴线单位长度上的水动力矢量；FD为垂直作用于构件轴线并在构件轴线和速度μ平面内单位长度上的阻力矢量；Fl为垂直作用于构件轴线并在构件轴线和dμ/dt平面内的单位长度的惯性矢量；μ为垂直于杆件轴线的水粒子速度矢量分量；dμ/dt为水粒子加速度矢量与杆件轴向垂直方向上的矢量；Cd为拖曳力系数；Cm为惯性力系数；A为杆件单位长度上的投影面积；V为杆件单位长度上的体积；ρ为水的密度。

Morison公式的计算精确度很大程度上取决于桩腿惯性力系数Cm和拖曳力系数Cd。本计算根据DNV规范，采用与方柱相同的惯性力系数Cm=2.5和拖曳力系数Cd=2.4。

2.3 海流载荷

海流是大范围内海水的稳定、周期性流动，主要由海风、海水温度、盐度分布变化的因素而引起，是在设计海洋工程结构物水下部分必须考虑的载荷。海流速度可由静水海流和风海流两个分量组成，计算公式如下[8]：

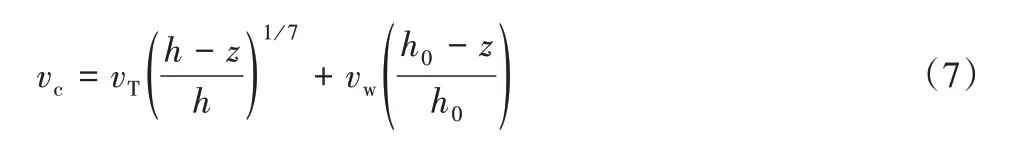
式中：vT为静水水面的海流速度，m/s；vw为风海流速度，m/s；h0为风海流的参考深度，m，一般取h0=50 m；z为距离静水水面的深度，最大取值大于h0，h为静水水面距离海底的深度，m。

在平静海况下，海流速度可直接取值为静水海流速度，但是在风暴海况下，只计算静水海流是不准确的，必须引入风海流分量。风海流的计算公式如下[8]：

式中：vR为参考高度10 m、时距为1 min时的风速，m/s。

海流载荷是以海流速度为自变量的函数，计算公式如下[14]：

式中：v为设计流速；ρ为海水密度；Cd为拖曳力系数；A为结构与流速垂直平面的投影面积。

取风暴自存工况下的海流流速为1.7 m/s，正常工作工况下的海流流速为1 m/s。

3 静态分析

3.1 原理

结构静态分析主要是求解桩腿在静载荷作用下的响应，包括线性和非线性两方面。线性静力主要用来研究桩腿的位移、变形、应力、应变甚至弯矩等等，非线性静力分析主要针对大变形、塑性、蠕变应力钢化等给出数值解析方法[2]。

静态分析的基本流程是将整体结构进行离散化处理后，分成多个单元和单元节点，并对其完成编号；接着建立各单元的刚度矩阵，组集得到整体结构的全局刚度矩阵，最后以各节点的位移为未知量，以节点之间静力平衡为条件，求解各节点的位移，最后根据求得的节点位移求出各单元的应力。

静态分析利用基于位移的节点有限元方法进行线性静态分析，得到了一个线性平衡方程组[15]，如下所示：

式中：[K]为由单元刚度矩阵求得的结构全局刚度矩阵；{u}为未知的节点位移矩阵；{F}为节点载荷和单元载荷的求和矩阵。

本节使用线性静力研究风电安装船在风暴自存和正常工作两种工况下，不同桩腿底部约束条件的变形和弯矩情况，主要考虑0°（随浪）、45°、90°、135°、180°（迎浪）5种浪向角。

3.2 风暴自存工况

刚性固定模型和桩土耦合模型在风暴自存工况下的位移云图如图6所示，位移单位为m。从图中位移对比中可知，不管是采用刚性固定模型还是桩土耦合模型，模型最大位移出现点位置基本一致，位移分布也基本一致。这是由于桩腿较长，在风载荷对船体的作用下，桩腿承受较大的弯矩而产生变形，故最大位移出现在上部船体或者桩腿上。与刚性固定模型不同的是，桩土耦合模型的桩靴部分都有较小的位移，这是由于考虑土的竖向和横向的承载力，使得安装船在受到载荷时，桩靴挤压泥层，从而产生微小位移。

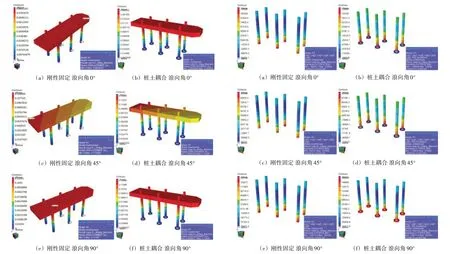
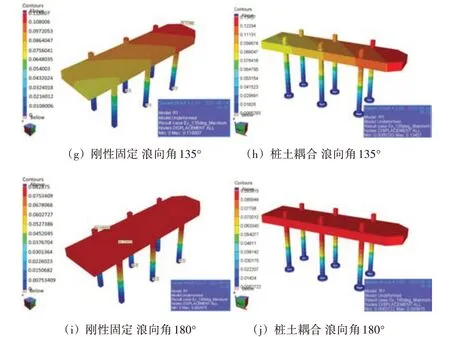
图6 风暴自存不同浪向角下的静态分析位移结果

刚性固定模型和桩土耦合模型在风暴自存工况下的弯矩云图如图7所示，弯矩单位为kN·m。从图中弯矩结果对比可知，刚性固定模型最大弯矩出现位置与桩土耦合模型最大弯矩出现位置一致，皆为桩腿底部。不同的是，刚性固定模型最大弯矩为桩腿刚性固定处，桩土耦合模型的最大弯矩出现在桩靴底部。刚性固定模型中桩腿的弯矩底部最大，随着高度逐渐变小；而对于桩土耦合模型，桩靴部分的弯矩为负值且为极小值，在桩靴与桩腿的连接处，弯矩方向突然转变，出现一个较大的正值。出现该种情况的原因可能是因为采用等效杆单元在桩腿与桩靴处突然改变截面直径和刚度，实际情况下，该处的弯矩过渡会较为平缓。

图7 风暴自存不同浪向角下静态分析弯矩结果

3.3 正常工作工况

刚性固定模型和桩土耦合模型在正常工作工况下的位移云图如图8所示，位移单位为m。

图8 正常工作不同浪向角下静态分析位移结果

刚性固定模型和桩土耦合模型在正常工作工况下的弯矩云图如图9所示，弯矩单位为kN·m。

图9 正常工作不同浪向角下静态分析弯矩结果

正常工作工况下，刚性固定模型与桩土耦合模型的计算结果与风暴自存工况类似，桩土耦合模型的计算值较大，表明土层对桩腿有一定影响，但是影响并不明显。可在采用刚性固定模型计算时适当加入一定的安全系数用于考虑桩土耦合效应。

4 分析结果

提取图7、图8中风暴自存工况下的最大位移值与最大弯矩，如表4所示；提取图9、图10中正常工作工况下的最大位移值和弯矩值，如表5所示。为方便对比分析，图中位移的单位由m转为mm。

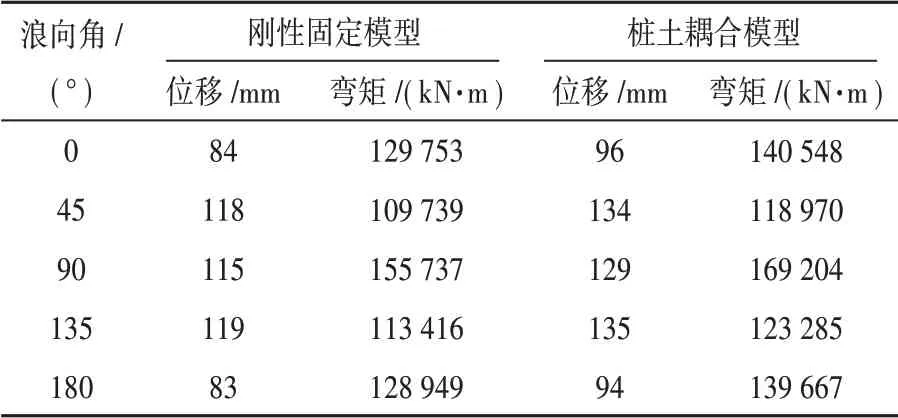
表4 风暴自存工况位移和弯矩最大值对比

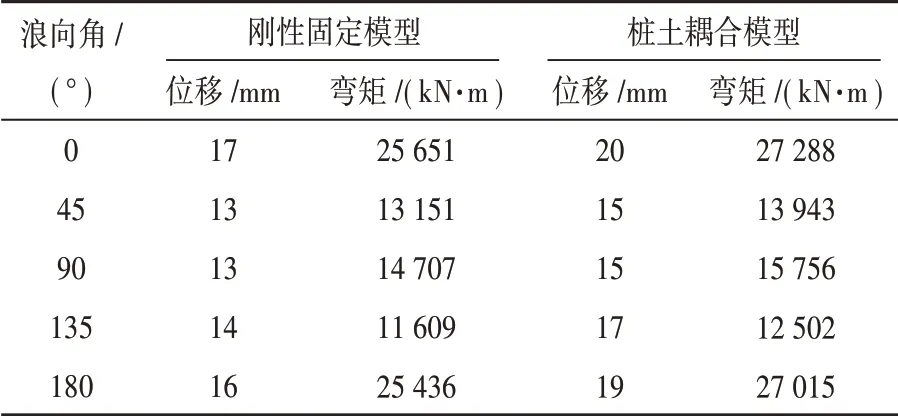
表5 正常工作工况位移和弯矩最大值对比

综合分析和比较表4、表5，可以得到以下结果。

（1）在风暴自存工况下，最大位移为115～119 mm，与整个平台主尺度相比位移响应值合理，平台整体符合刚度要求。

（2）无论是风暴自存工况和正常工作工况下，桩土耦合模型的位移和弯矩分析结果均比刚性固定模型的结果大，这是由于桩土耦合模型考虑了泥面以下位置与土层的相互作用。在工程上使用桩土耦合模型分析更加保守、安全，但计算模型更为复杂，计算耗时更多。通过对两种工况下刚性固定模型和桩土耦合模型的位移和弯矩的差异度发现，两种工况下位移差异均不超过15%，弯矩差异均不超过10%，刚性固定模型可以保障基本计算精度。

（3）在风暴自存工况下，当浪向角为45°、90°、135°时，刚性固定模型位移为115～119 mm，桩土耦合模型位移为135～139 mm，刚性固定模型和桩土耦合模型都反映出现较大的位移。而当浪向角为0°、180°时，刚性固定模型位移为83～84 mm，桩土耦合模型位移为94～96 mm，位移相对较小。这说明了在风暴自存工况下，平台整体迎浪或随浪较为安全，横浪较危险，应尽量避免船身侧面正对风浪流载荷。

（4）在正常工作工况下，刚性固定模型在5个浪向角下位移为13～17 mm，桩土耦合模型位移为15～20 mm，刚性固定模型和桩土耦合模型都反映了各个浪向角下位移范围较小，位移值较小。这说明了正常工作工况下的风浪设计值合理。在该设计范围内的工况，各个浪向角均可以保证风机安装的精度。

5 结束语

本文采用SESAM软件的GeniE模块建立了桩腿及风电安装船主船体的梁系简化有限元模型，得到了风暴自存工况和正常工作工况下在不同的浪向角、不同的底部固定条件下的位移和弯矩，从有限元分析的维度论证了使用桩土耦合分析比刚性固定分析更加精确，但使用刚性固定模型可满足基本的分析精度；从桩腿设计的维度论证了桩腿的刚度可以经受风暴自存工况和正常工作工况两个设计工况的考验，但在风暴自存工况下，应尽量保证处于迎浪或随浪的安全环境，尽量避免船身侧面正对风浪流载荷，且本文的计算仿真过程对于其他船舶的风浪流载荷分析有一定的借鉴意义。