基于双无迹变换的锂离子电池SOC估计研究

封居强，孙亮东，蔡 峰，伍 龙，卢 俊

(1.淮南师范学院机械与电气工程学院，安徽淮南 232038；2.安徽理工大学深部煤矿开采响应与灾害防控国家重点实验室，安徽淮南 232001；3.淮南市矿用电子技术研究所，安徽淮南 232002)

锂离子电池以其长寿命、高安全可靠性、高能量密度、低自放电率等优点，成为电动汽车的主要选择，其性能状态的好坏直接影响到电动汽车是否能够长期正常稳定运行。因此，需要开发行之有效的电池管理系统(battery management system，BMS)，用于实时监测及诊断锂离子电池的状态。BMS 中最主要和最核心的研究内容就是精确估计电池的荷电状态(state of charge，SOC)，SOC表示在某一温度下，存储在电池内可供设备使用的电量与满电状态下电池能够存储的总电量之间的百分比，是表征锂电池剩余可用电量的一项重要指标。研究早期，锂电池一般使用在一些较为基础的设备上，性能要求较低，所以使用的估算方法也相对简单，能大致满足估算要求即可。常用的估算方法包括安时积分法[1]、内阻分析法、开路电压法[2]、放电实验法等。这些方法都是离线估算方法，考虑因素较为简单，累积误差较大，估算精度也较低。

卡尔曼滤波算法(Kalman filter，KF)是目前使用最为广泛的一种最优的估计算法。该算法根据前一时刻的状态变量的最优值以及观测变量真实值与估计值的差来估算当前时刻状态变量的估计值。但该算法要求系统必须是线性的，而电池系统是典型的非线性系统，锂电池开路电压、内阻、端电压及荷电状态等在电池工作条件下都呈现出强烈的非线性变化。为将KF 算法应用于非线性领域，后发展出扩展卡尔曼滤波(extended Kalman filter，EKF)算法[3]，将非线性系统线性化，在测量结果和估计结果附近进行一阶泰勒展开[4]，但估计结果会引起泰勒截断误差，高阶项被忽视，有可能导致滤波发散；EKF 算法在每一次循环估算时都需要重复计算雅可比矩阵，极大增加了系统计算复杂度[5]。

为了克服EKF 算法的上述缺点所带来的一系列问题，将EKF 使用的非线性系统强制线性化的方式转换为对系统状态变量的概率密度分布的近似值，将无迹变换(unscented transform，UT)和卡尔曼滤波算法相结合，以无迹变换为基础，采用合适的采样策略来逼近状态变量分布，这种算法称为无迹卡尔曼滤波算法(unscented Kalman filter，UKF)[6]。UKF 可以有效地提高对非线性分布统计量的估算精度，但这很大程度上取决于电池模型的精度和系统噪声的预定变量，系统噪声的预定变量设置不当，会导致系统误差，甚至造成系统发散[7]。

基于以上研究，本文为更加准确地表征锂离子电池的动态特性，建立改进的PNGV 模型[8]，同时在保证系统稳定性的前提下，采用改进的UKF 算法对锂离子电池的SOC进行估计，并采用两个非线性变换来提高系统的精度[9]。改进卡尔曼增益，增加自适应动态增益调节模块[10]，解决了BMS 状态突然变化时SOC值振荡的问题。

1 等效电路模型的建立与参数辨识

1.1 电池模型的建立

锂离子电池是具有复杂性噪声特点的非线性动态系统，且其工作状态受环境和负载工况影响较大，因此建立一个能够准确可靠地反应锂离子电池工作特性的模型十分重要[11]。目前，最常用模型有三类：依据电池内部化学反应而建立的电化学模型、模拟人脑工作的神经网络模型以及使用电子元器件建立的等效电路模型[12]。电化学模型搭建相当复杂[13]，几乎没办法应用到电动汽车上；神经网络模型[14]在样本数据不够的情况下估算误差将会很大，并且算法的收敛性和稳定性暂时还得不到保证；等效电路模型由理想元器件(电阻、电容、可控电源等)构成，采用线性变参数方法模拟锂离子电池非线性工作特性，精度往往相对较低，但简单而实用的模型结构会缩短开发周期，降低开发成本。

等效电路包含很多种模型结构，常见的包括Rint 模型、RC 模型、Thevenin 模型和PNGV 模型。其中Rint 模型电路参数简单，但不能反映电池的动态特性；RC 模型弥补了Rint 模型的不足，但电路方程非常复杂，模型状态方程的建立比较困难[15]；Thevenin 模型具有Rint 模型和RC 模型的优点[16]，但该模型将电池的内阻作为一个定值，不能代表电池电压的稳态变化，也不容易估计电池的运行时间；PNGV 模型[17]弥补了Thevenin 模型相对简单、易于识别模型参数的缺点，但不能完全代表电池的松弛效应，本文对其进行了改进，通过另外一个平行RC 电路模拟了原始PNGV 模型中未表示的松弛效应，使模型更能充分地满足锂离子电池在复杂工况下参数测量的要求。改进后的PNGV 模型如图1 所示。

图1 中，E是理想电压源，R0是欧姆电阻，RS和RL为极化电阻，CS和CL为极化电容，电池充放电电流以I为参数，UL为电池端电压。其中RS和CS组成的并联电路具有较小的时间常数，用来模拟电流突变时电压快速变化的过程；用RL和CL组成的并联电路模拟电流突然变化时电压的快速变化，因此它们的时间常数比较大。

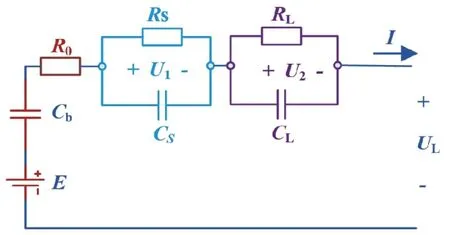
图1 改进的PNGV 模型

1.2 参数辨识

针对锂离子电池在充放电过程中的内阻差异，对选定的锂离子电池进行主要充电过程和主要放电过程的HPPC 测试[18]。主要放电过程的HPPC 测试步骤如下[19]：

步骤1：首先将锂离子在标准环境下进行放电，静置2 h后，以恒流恒压将锂离子电池充电至100%SOC。其中，充电电流设为1C(68 Ah)，充电电压设为4.2 V，截止条件设为3.4 A。

步骤2：将锂离子电池静置12 h 后激活，测量并记录电池两端电压值。

步骤3：在锂电池上进行电流脉冲测试。先以1C电流放电10 s，然后静置40 s，再1C电流充电10 s，使电池恢复放电前的SOC值，完成一组脉冲充放电测试。

步骤4：以0.5C电流开始放电，放电12 min(剩余电池SOC90%)，然后静置1 h，截止条件为3 V。

步骤5：重复步骤(3)和(4)，每次循环放电10%的容量，分别记录SOC为0.9、0.8、0.7…0.1 时的相关数据，为下一个参数识别做好准备。

同样的，改变上述步骤4，以0.5C电流开始充电，充电时间为12 min 并记录实验数据，这就是主充电过程的HPPC 测试过程。在HPPC 测试过程中，单组锂离子电池电压的变化如图2 所示。

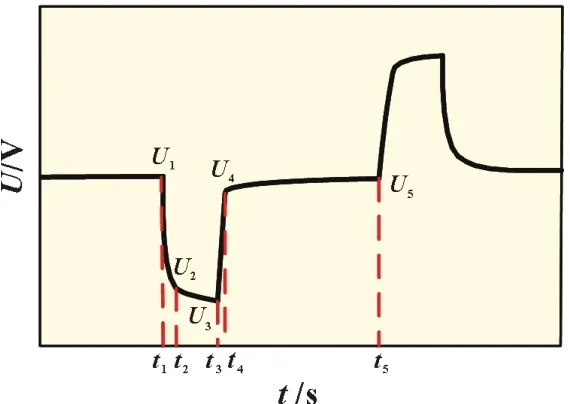
图2 HPPC 测试中电压曲线示意图

由HPPC 测试步骤可以得出，电池在开始放电(t1-t2)和停止时(t3-t4)端电压的突然变化是由欧姆内阻引起的。因此，通过欧姆定律可以计算欧姆内阻，如式(1)所示：

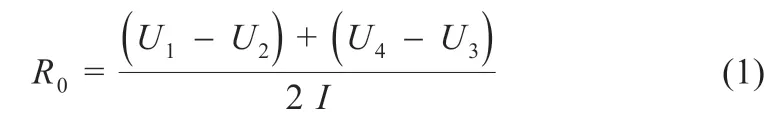
当锂离子电池处于HPPC 测试的脉冲放电阶段时，将电流流动的正方向设为Ib。根据图1 中电压和电流的参考方向，可以列出KCL 和KVL 方程，如式(2)所示：

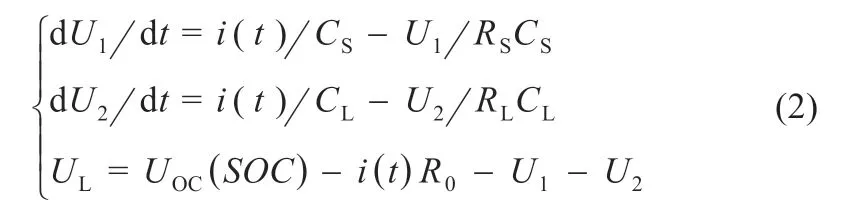
式中：U1、U2分别为RS和CS与RL和CL组成的并联电路的端电压。电池在t1-t3期间持续放电10 s，其余时间保持静置状态。通过对两个串联的RC 电路进行时域分析，得到RC 网络的电压如式(3)所示：

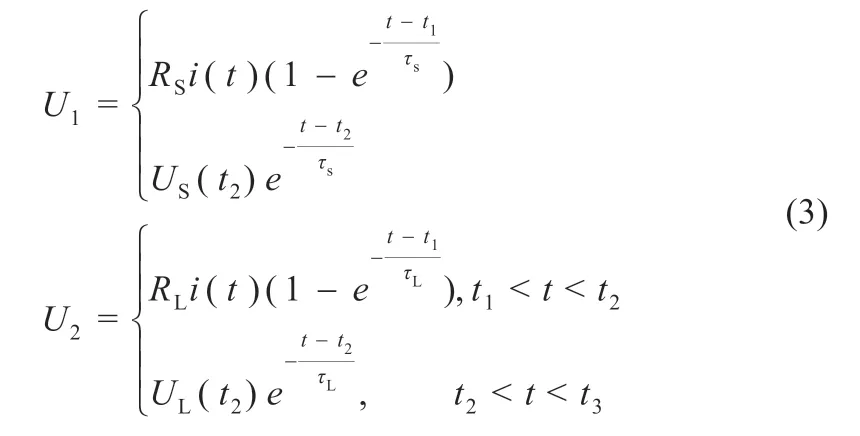
式中：t1为放电开始时间；t2为放电停止时间；t3为搁置停止时间；τS为RS和CS并联电路的时间常数；τL为RL和CL并联电路的时间常数。其中τS和τL的计算公式如式(4)所示：

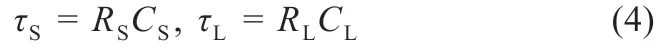
锂离子电池在放电时，极化电容CS与CL处于充电状态，并联连接的RC 电路电压呈指数上升，电池从放电到静置，电容CS和CL分别并联电阻放电，指数下降模型中R 和C 的电压值与电池的SOC有关,利用MATLAB 对HPPC 测试数据曲线进行拟合，再利用待定参数法即可计算出模型中RS、RL、CS、CL的值。取出图2 中U4到U5的实验数据，根据HPPC 测试步骤，t2-t3期间，极化电容对极化电阻放电，是两个RC 电路串联的零输入响应，电池端电压输出方程如式(5)所示：

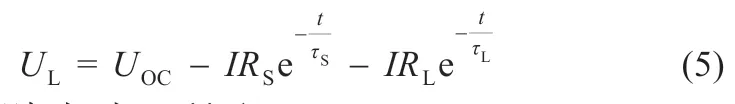
简化参数识别，如式(6)所示：

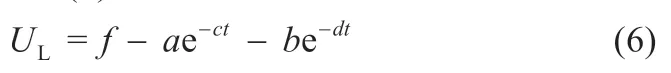
以f,a,b,c,d为待定参数，以式(6)为目标方程进行双指数曲线拟合。根据双指数曲线的拟合结果，通过比较式(5)和(6)，得到参数识别结果如式(7)所示：

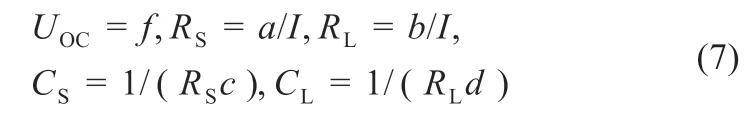
2 SOC 估计算法

2.1 无迹卡尔曼滤波算法

非线性变换是UKF 算法的核心，其基本原理是用适当的采样点分布来表征随机变量的概率密度分布。结合锂离子电池组改进的PNGV 模型，以SOC为状态方程的变量，开路电压为观测方程的变量，构造了状态方程和观测方程的表达式。经过非线性函数变换得到Sigma 数据点，然后通过加权得到变换后的均值和协方差，得到它们的加权因子。SOC估计的具体方法和步骤[20-21]如下：

(1)构造Sigma 点集

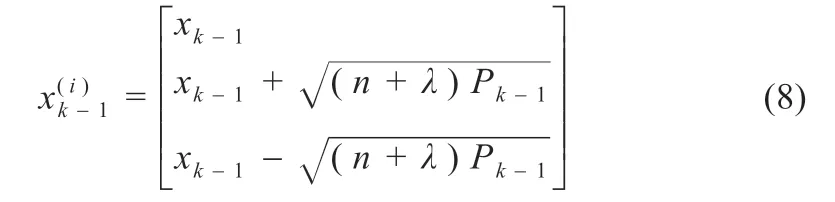
(2)计算权重

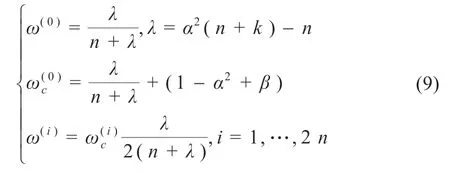
(3)更新状态变量

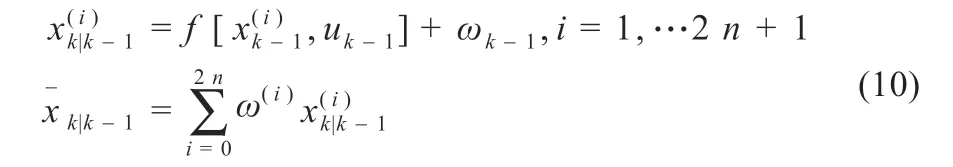
(4)更新状态方差

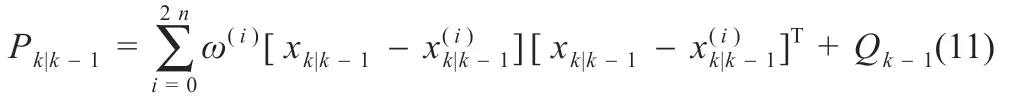
(5)再次计算Sigma 数据点序列、更新观测值

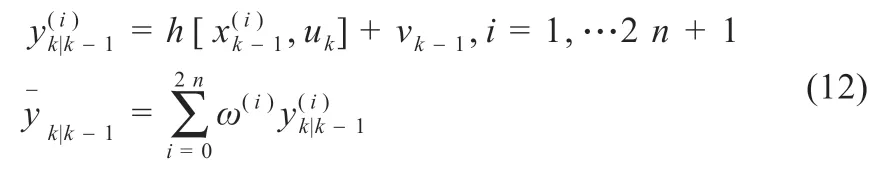
(6)计算均值和协方差

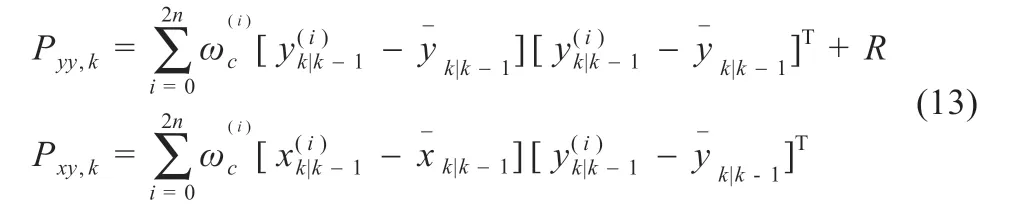
(7)计算增益矩阵

(8)状态和误差协方差更新

2.2 双无迹变换卡尔曼滤波算法

为了提高UKF 算法估计SOC的精度和速度，本文通过两个非线性变换对系统的闭环电压进行预测[22]，采用参数的动态修正提高估计值收敛速度。改进算法的计算过程示意图如图3 所示。

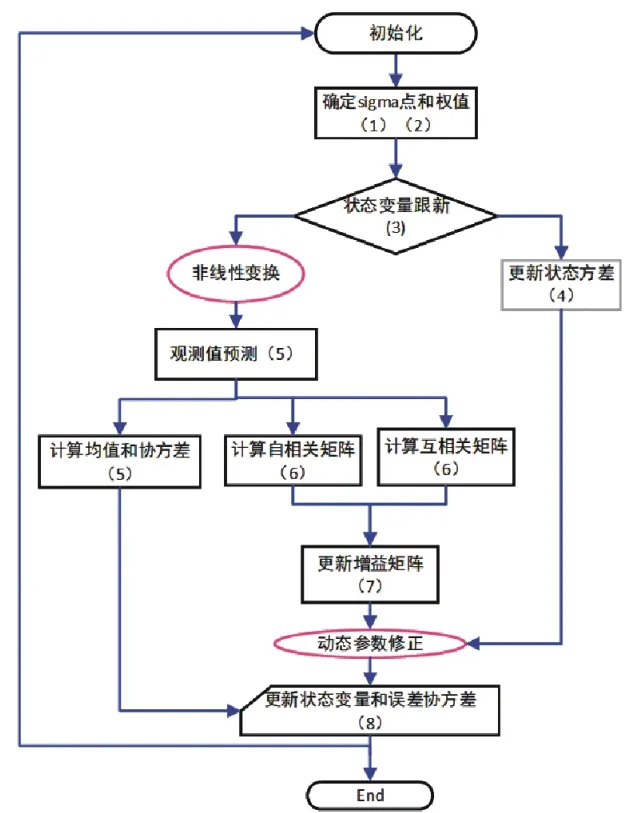
图3 改进算法的迭代流程

图3 黑色方框中的内容以及(1)、(2)…(8)为上文中UKF估计SOC的步骤；红色椭圆图中的非线性变换和动态参数修正为本文改进的部分。

通过非线性变换得到两个Sigma 数据点序列的SOC值及其对应的权值。然后通过状态方程得到两个Sigma 数据点的预测值，再加权求和处理得到单个SOC预测值。对预测结果再次进行非线性变换，并将变换结果应用到观测方程中，以提高估计精度。

2.3 动态参数修正

当卡尔曼滤波进行滤波估计时，如果系统的状态突然发生变化，往往跟踪真实状态很慢，从而降低了估计精度。本文通过增加动态参数修正模块对其进行改进，使算法在估计过程中具有更好的跟踪效果。

若工作电流变化满足式(16)所示条件：

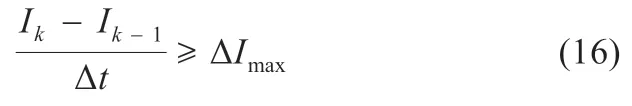
式中：ΔImax为当前最大变化设定值。即当工况电流发生跳变时，则改进的卡尔曼增益和状态估计测量值更新，如式(17)所示：

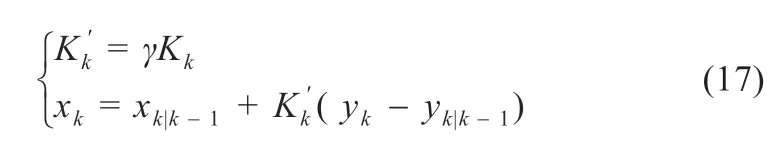
式中：γ为增益因子，其值可以大于1，从而加速算法估计过程中估计值的收敛速度。

为了增强系统的稳定性，将增益设置为动态值，并根据电流的变化自动调整。在工作条件下，当电流变化较大时，可动态调整增益为较大的值，使算法估计收敛速度增大。当电流变化稍微平缓一点时，增益值会逐渐恢复到原来的值。然后更新动态增益计算和状态估计测量，如式(18)所示：

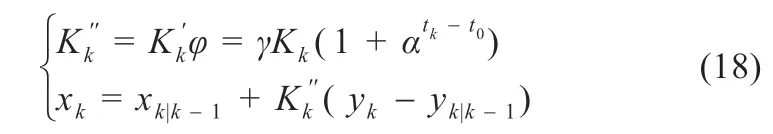
3 实验结果与分析

3.1 模型验证

本文选用容量为68 Ah 的三元聚合物锂离子电池进行测试，测试过程设置采样率为0.1 s，采样精度为±0.05%、电压分辨率为0.1 mV、电流分辨率为0.1 mA。首先将主充电HPPC实验和主放电HPPC 实验的参数引入到改进的PNGV 模型中，实验得到的终端电压对比曲线如图4～7 所示。

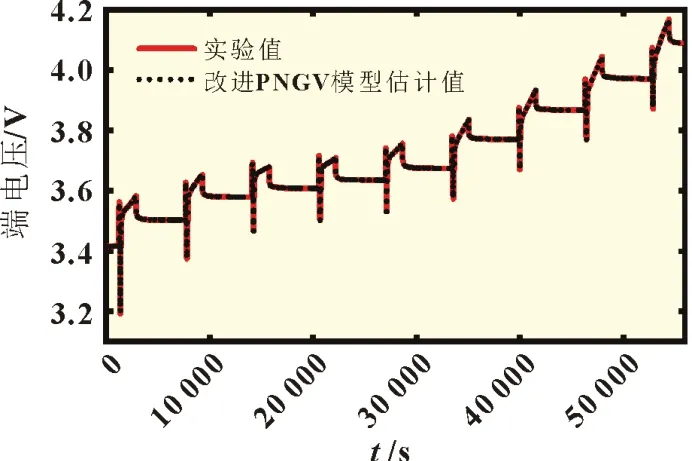
图4 充电端电压及电压估计值

图6 和图7 所示的改进PNGV 模型估计值能够较好地估计和跟踪充放电过程中的端电压。图6 和图7 所示的主充电过程HPPC 实验的最大参数识别误差小于0.015 V，主放电过程HPPC 实验的最大参数识别误差小于0.01 V。产生误差主要有三个原因：其一是采样分辨率造成的0.1 mV 误差；其二是采样间隔0.1 s 期间，默认模型的参数为不变值而造成的误差；其三是模型精确度造成的估计误差。其中前两种原因可认为量化误差，对于电流平稳时0.3 mV 的误差影响较大，侧面也反映了该模型的精确度，为SOC精准估计奠定了基础。

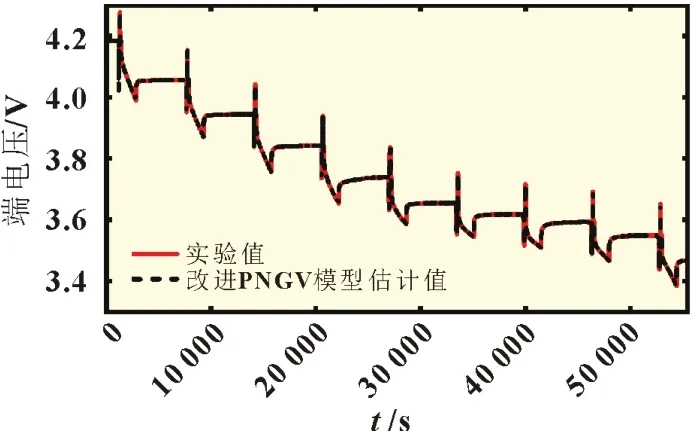
图5 放电端电压及电压估计值

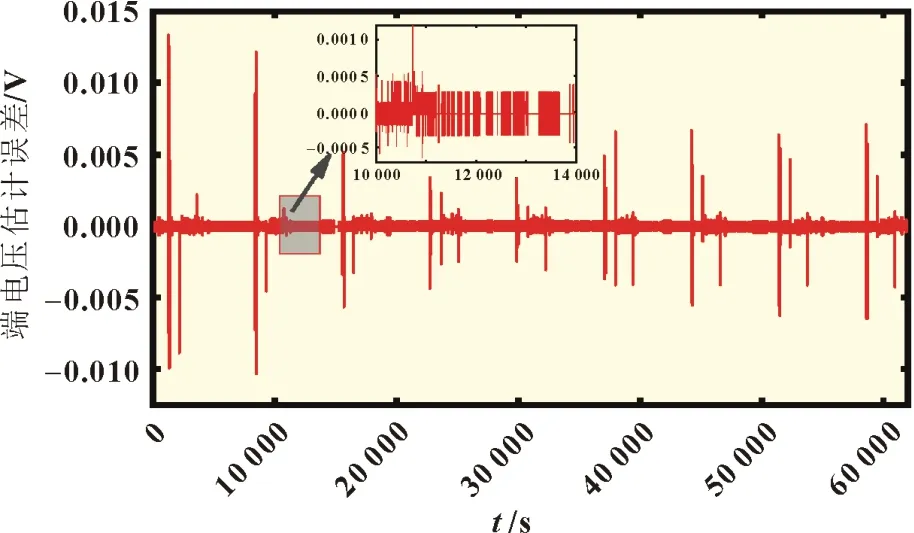
图6 充电端电压估计误差

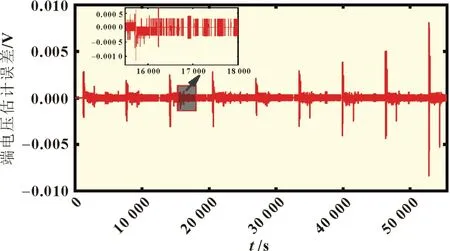
图7 放电端电压估计误差

3.2 混合放电比实验

为了验证改进算法的准确性和稳定性，设计了混合放电比实验，更准确地分析和描述锂离子电池的工作特性。在实验过程中，结合5 种不同放电电流倍数的变换器仿真实验，实现了复杂变换器条件下SOC估计性能测试。放电电流曲线如图8 所示。

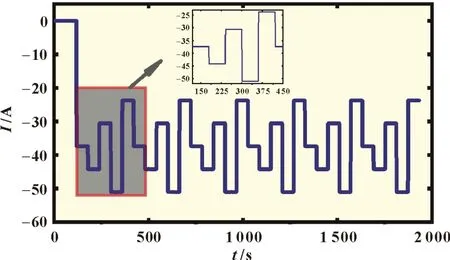
图8 混合放电比实验的电流曲线

依据混合放电比实验数据，基于改进的PNGV 模型进行了安时积分法、EKF 法、UKF 法和本文改进的UKF 法进行SOC估计，并与理论值(双指数曲线获得)进行比较，结果如图9 所示，SOC估计的误差如图10 所示。通过最大误差、平均绝对误差(MAE)和均方根误差(RMSE)对四种方法的估计误差进行分析对比，如表1 所示。

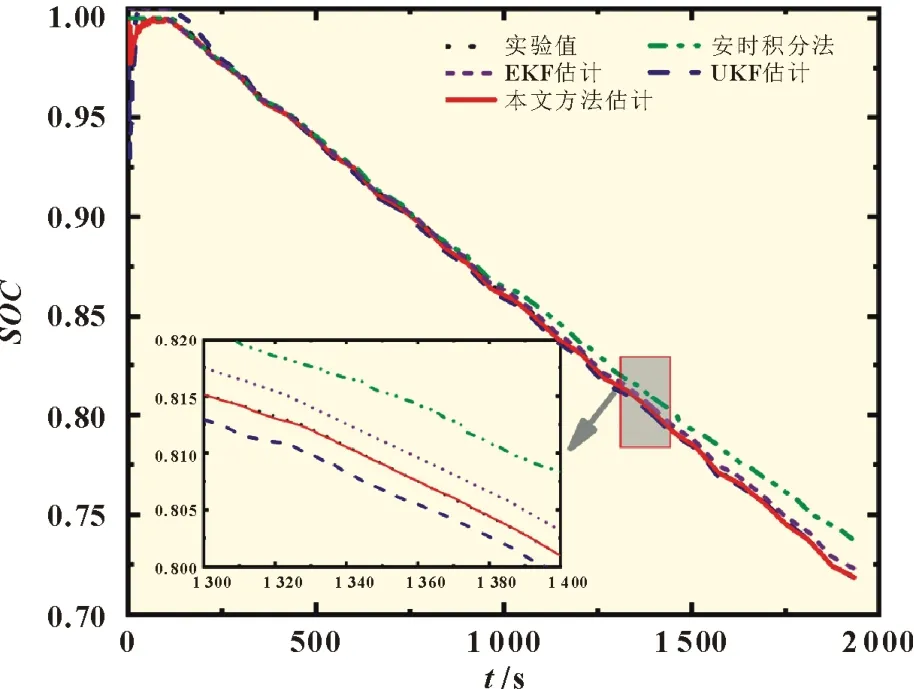
图9 不同方法的估计结果比较

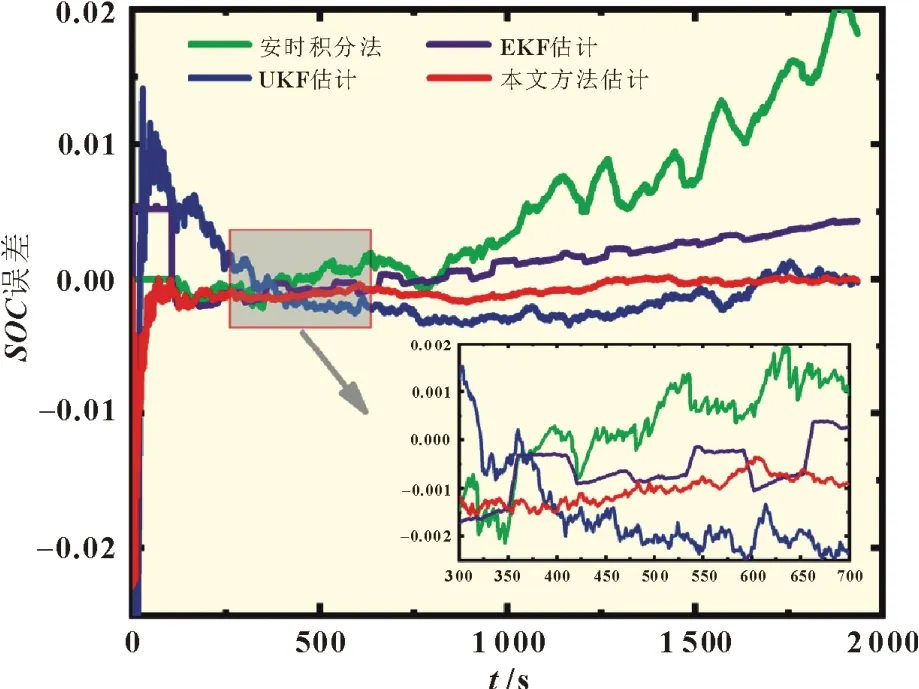
图10 不同方法估计误差比较

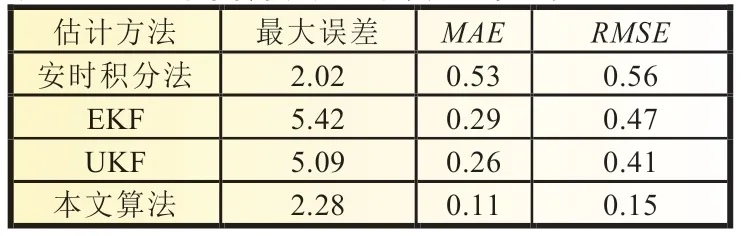
表1 不同方法估计误差对比分析 %

由图9、图10 的曲线和表1 的数据可得，EKF、UKF 和本文估计方法均在初始时产生最大误差，分别为5.42%、5.09%和2.28%，安时积分法存在累加误差，因此在接近结尾时产生了最大误差，为2.02%。

由图10 可得，由于混合放电比实验电流周期性变化，且相对剧烈，安时积分法、EKF 和UKF 估计方法产生周期性误差，本文算法受电流变化影响相对较小。表1 中，本文算法的RMSE为0.15%，表明鲁棒性较好。UKF 算法的RMSE值相对最小，但仍是本文算法的3 倍，也解释了其它方法受电流周期性变化影响。

由图10 和表1 可知，经过372 s 后，安时积分法除外的三种方法均能保持在0.3%以内的估计误差，平均绝对误差为0.29%、0.26%和0.11%，相比较，本文算法精度至少提高了58%。

4 总结

为了充分满足锂离子电池在复杂工作环境下参数测量的要求，本文建立了描述动态环境下电池状态的二阶电路模型。除此之外,为了解决当脉冲电流变化率较大时，算法不理想、估计误差较大、算法跟踪效果不理想等问题，本文采用两个非线性变换预测系统的闭环电压，采用动态功能模块提高卡尔曼增益改进UKF 算法。以68 Ah 的三元聚合物锂离子电池为对象进行了相关实验。通过HPPC 测试和混合放电比实验验证了模型和算法在不同状态下的可行性。结果表明，改进的PNGV 模型具有较高的精度，改进的算法能够精准估计SOC值，且稳定性和一致性较强。