新课标下尺规作图新路径:联想,整合,生成
2022-11-25合肥市第四十八中学丁永愿
⦿合肥市第四十八中学 何 平 丁永愿
1 问题提出
初中新课程标准增加了“过直线外一点作已知直线的平行线”的尺规作图内容.如图1,过点P作直线m的平行线n.
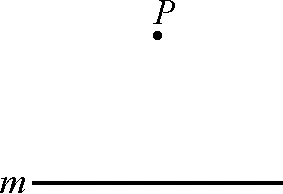
图1
2 解法赏析
2.1 联想发散
由题意发散联想出具有平行性质的图形并画出相应的草图.根据学生经验不难得到出现平行的基本图形有:三线八角图、中位线、A(X)形相似结构、平行四边形等.如图2所示.

图2
2.2分析整合
学生具备五大基本作图经验,基本作图可以实现“作等线段,作等角,作垂直,作中点,作角平分线” 等功能,其余的尺规作图是在五大基本作图的基础上整合而成的[2].在分析整合时要注重可行性、合理性,所谓可行性是图形的定义或判定中的关键词能与五大基本作图的功能对应,如平行四边形的判定“两组对边分别相等的四边形是平行四边形”,关键词是两组对边相等,与五大作图中的“作等线段”功能可以对应上,作平行四边形具有可行性;作图也要兼顾合理性,若图形的内涵太丰富,则作图要求也就越多,如正方形,虽然可作,但过于繁琐,可有选择性地放弃.
2.3 演绎生成
法1:如图3,过点P作直线l交直线m于点A,确定∠1;作∠2=∠1(或∠3=∠1),得直线n.
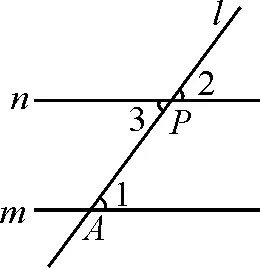
图3
法2:如图4,过点P作直线m的垂线l交直线m于点A;过点P作直线l的垂线n.

图4
法3:如图5,在直线m上确定点A,B,作射线AP,过点A作∠PAB的角平分线AC;以点P为圆心,AP为半径作弧交角平分线AC于点Q,连接PQ得到直线n.
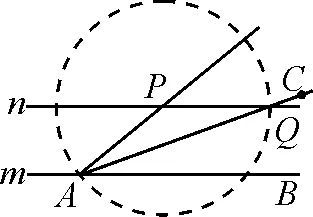
图5
法4:如图6,在直线m上确定点A,B,在线段AP的延长线上截取点O,使AP=PO;连接OB,作线段OB的中点Q,连接PQ得到直线n.
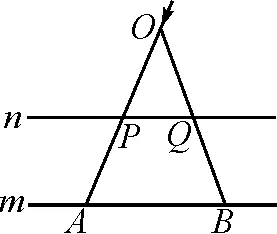
图6
法5:如图7,在直线m上任意确定点A,在线段AP的延长线上任意确定点O,以点O为圆心,OA为半径作弧交直线m于点B;连接直线OB,以点O为圆心,OP为半径作弧交直线OB于点Q, 连接PQ得到直线n.

图7
法6:如图8,在直线m上任意确定点A,B,作线段AP;以点P为圆心,AB为半径作弧与以点B为圆心,AP为半径作的弧交于点Q,连接PQ得到直线n.

图8
法7:如图9,在直线m上确定点A,B,连接BP,作线段BP的中点O;作射线AO,在射线AO上截取OQ=AO,连接PQ得到直线n.

图9
法8:如图10,在直线m上确定点A,连接AP,以点A为圆心,AP为半径作弧交直线m于点B;以点P为圆心,AP为半径作弧与以点B为圆心,AP为半径作的弧交于点Q;连接PQ得到直线n.

图10
法9:如图11,在直线m上确定点B,连接BP;作线段BP的中垂线l交直线m于点A,交线段BP于点O;在线段AO的延长线上截取OQ=AO,连接PQ得到直线n.

图11
法10:如图12,在直线m上任意确定点B,连接BP;作线段BP的中点O;以点O为圆心,OB为半径作⊙O交直线m于点A;作射线AO与⊙O交于点Q,连接PQ得到直线n.

图12
法11:如图13,在直线m上任意确定点A,B;以点A为圆心,BP为半径作弧与以点B为圆心,AP为半径作的弧交于点Q;连接PQ得到直线n.

图13
法12:如图14,取一点O,以点O为圆心,OP为半径作⊙O交直线m于点A,B;以点B为圆心,AP为半径作弧交⊙O于点Q;连接PQ得到直线n.

图14
3 结论
3.1明确尺规作图的教学意义
对于尺规作图,师生要改变认知,不能仅仅是机械模仿、简单组合,在探究该问题时几乎覆盖了初中阶段的所有图形,如三线八角、三角形、四边形、圆、相似三角形等,并在整个探究阶段对这些图形的定义、性质、判定也进行了综合系统的复习,对学生的几何直观、演绎推理、结构化思维、规范书写、语言表达、动手操作及发散思维等能力有极大的提高.同时,在教学过程中还能让学生感悟到思想方法的统一美、作图过程的理性美、作图表述的语言美、作图结果的方法美.
3.2注重基本图形的积累
联想图形是尺规作图中较难的一个环节,这是一个从无到有的生成阶段,有了联想的草图才能确定如何作下一步.而能够想到什么基本图形源于学习经验的积累以及对图形的熟悉与掌握程度.因此,学会积累常用的基本图形对解决尺规作图问题至关重要.
