依“标”靠“本”重基础 能力立意考素养
——浅析几道中考数学试题的“根”与“源”
2022-11-25泸州市教育科学研究所邹伦富
⦿泸州市教育科学研究所 邹伦富
1 引言
新的数学课程标准指出:数学素养是现代社会每一个公民应该具备的基本素养,数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能,更要发挥数学在培养人的理性思维和创新能力方面的不可替代的作用.2016年9月,教育部发布了《关于进一步推进高中阶段学校考试招生制度改革的指导意见》(以下简称《指导意见》).《指导意见》指出:要依据义务教育课程标准确定初中学业水平考试内容,提高命题质量,减少单纯记忆、机械训练性质的内容,增强与学生生活、社会实际的联系,注重考查学生综合运用所学知识分析问题和解决问题的能力.近年来,各省市初中学业水平考试和高中阶段学校招生考试试题的命制按照《指导意见》精神,积极探究,涌现了不少紧密贴合课程标准,牢牢扎根教材,体现能力立意,素养导航的试题.下面浅析近几年部分中考数学试题的“根”与“源”,供大家参考.
2 试题溯源
2.1植根教材正文


图1
评析:人教版教材八年级下册“勾股定理”一节中,介绍了运用“赵爽弦图”证明勾股定理的基本思路,即通过对图形的切割、拼接,巧妙地利用面积关系证明勾股定理.“赵爽弦图”曾被作为2002年在北京召开的国际数学家大会的会徽.一般地,涉及“赵爽弦图”的相关问题,需要弄清构成“赵爽弦图”中的两个正方形、四个直角三角形的边角以及面积间的等量关系.“赵爽弦图”沟通了代数与几何的联系,能够完美地体现数形结合思想,由“赵爽弦图”派生出的多种问题,对于考查学生的理性思维能力,提升核心素养具有较大的帮助,因此它备受各级命题者青睐.多年来,全国各省市州中考数学试题中,涉及“赵爽弦图”的试题可以说不计其数,而且常考常新,值得我们关注.

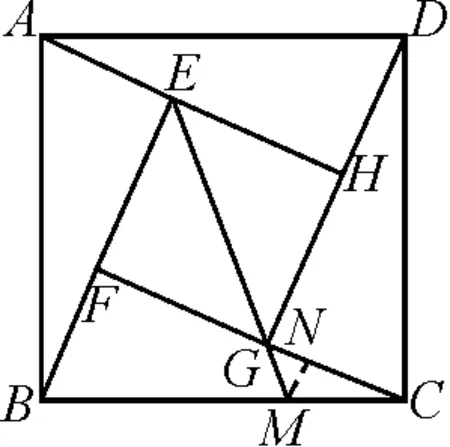
图2
2.2 源于阅读与思考
评析:人教版教材八年级下册第16页阅读与思考安排了阅读素材“海伦-秦九韶公式”,通过对这段材料的阅读,可以帮助学生了解已知三角形的三边求其面积的方法和求三角形面积的数学历史.本题将教材阅读与思考栏目提供的素材加以改编,给出三角形的半周长和c边的长,要求学生灵活使用公式,消元减参,转化为二次函数的最值问题,主要考查学生的阅读理解、数学运算能力,同时渗透了数学文化.
2.3 立足数学活动


图3
(1)求抛物线的解析式;
(2)在直线l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)已知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.
评析:本题的第(3)问实际上是已知抛物线的方程,在题设条件下求抛物线的焦点坐标,一般思路是运用勾股定理建立方程,再通过恒成立问题得出方程组,最后求出定点F的坐标.
人教版教材九年级上册第54页,在第二十二章学习结束之后安排了两个数学活动,其中活动2要求学生在平面直角坐标系中探求抛物线的解析式,渗透了抛物线的定义、焦点、准线等.本题的第(3)问可以看作是对该数学活动的延伸与拓广.
2.4 扎根实验与探究
例4(2021重庆中考第9题)如图4,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( ).
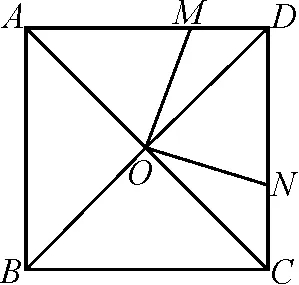
图4
评析:本题源于人教版教材八年级下册第十八章“平行四边形”中的实验与探究:

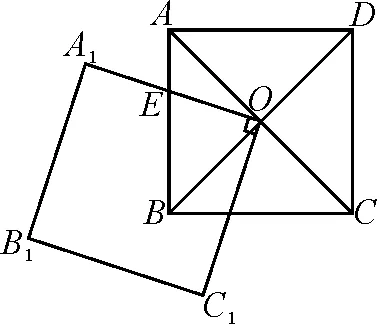
图5
本题以教材中的实验与探究为原型,适度改编和变形,给出四边形MOND的面积,逆向求正方形的边长.对于学生来讲,试题来源于教材,面目亲切,难度适中,体现了命题者考查学生数学素养,引导师生立足教材开展数学实验与探究的良苦用心.
2.5 拓展教材习题

图6
评析:本题源于人教版教材八年级下册习题的拓广探索“如图7,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2”.

图7
本题以教材习题为原型,在原题设条件下,增加线段AE,AD的长度,求出两个三角形重叠部分的面积.解决本题需要首先求出△ACB的边长,再添加辅助线,发现∠ADB=90°,且CD平分∠ADB,求出CD分线段AB之比,进而解决问题.此题与教材习题相比,问题的深度和广度都得到进一步的提升,对学生分析问题、解决问题的能力提出了较高的要求.本题源于教材,高于教材,考查学生灵活运用所学知识解决问题的能力,并且具有一定的选拨功能,是一道改编于教材的较为成功的试题.
3 启示与思考
启示一:深入学习新课程标准,研读教材,理解教材,弄清教材体系、体例和各个栏目的作用,认真体会编者的意图是开展教学工作的前提,要用教材教,而不是教教材.在平常教学中,教师要注意引导学生用好教材,结合教材安排的阅读素材、实验与探索、数学活动等,指导学生开展数学阅读、数学实验、数学活动;适时安排一些具有针对性的研究性学习课题,对拓展学生的视野,提高分析问题、解决问题的能力,进而提升数学思维能力,培养学生数学核心素养,无疑具有较大的帮助.
启示二:当前,一些学校数学教学中还存在着教学脱离课程标准和教材,盲目使用教辅资料的现象,教师忙于归纳各种题型和套路,学生忙于机械“刷题”,课堂教学容量过大,教学节奏过快;教学过程中,学生独立思考、感悟、反思的时间不多,师生交流、碰撞、合作的机会较少;所用的资料和考题绝大多数来自于现成的出版物或者网络,缺少改编、自编、原创试题,影响教学质量的进一步提升.因此,建议教师在教学中要认真揣摩课程标准,研究回归教材的具体措施,增加整合、激活、落实教材的环节,细化对教材各个栏目作用的研究;鼓励教师立足教材,积极开展改编、自编、原创试题的研究,形成具有校本特色的教材拓展资源,提升资料、试卷的针对性,切实提升学生的数学素养.
