基于PBL模式的初中数学教学思考
——“二次函数”第一课时课堂实录与思考
2022-11-25苏州高新区实验初级中学蔡春艳
⦿苏州高新区实验初级中学 蔡春艳
1 引言
PBL模式是一种以问题为导向的教学方法(problem-based learning,PBL),由美国的神经病学教授 Barrows 首创.它遵循以学生为中心,强调学生的主动学习,发挥学生的主体性,使学习者投入于问题中,通过学习者的自主探索和合作交流来解决问题,从而学习到问题中隐含的知识,并在此过程中发展解决问题的能力和自主学习的能力[1].
笔者最近参与了一节苏州市评优课“二次函数”的磨课过程.“二次函数”是初中数学的核心内容,这一章的逻辑结构与一次函数相似,是对函数知识的完善和提高.第一课时的重点为理解概念,如果按照传统模式,理解概念—应用概念,学生会缺乏学习课程的新鲜感,也无法从整体上理解二次函数.课程标准提出,“学生的学习应当是一个主动的过程.教学活动应引导学生在真实情境中发现和提出问题,分析和解决问题”[2].PBL理念与课程标准一致,因此笔者尝试采取PBL理念,即基于问题展开学生的学习,对教学过程作出梳理,供研讨.
2 课堂实录
2.1 环节(一)——创设情境,引入新课
师:同学们好,我来自苏州新区实验初中,昨天开车来到我们常熟外国语学校.
如图1,在这段运动过程中涉及哪几个量?
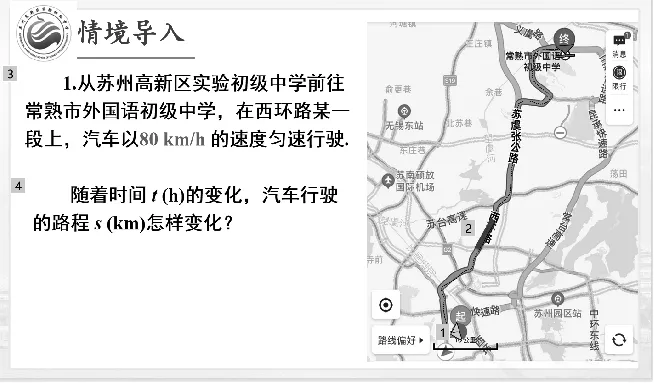
图1
生:时间、路程、速度.
师:这里的速度是常量,路程S和时间t是变量.这两个变量之间是什么关系?
生:S=80t.
师:S是t的函数吗?为什么?
生:是的.因为在这个变化过程中有两个变量S和t,对于t的每一个值,S都有唯一的值与它对应.
师:这是什么函数?
生:正比例函数.
师:正比例函数也是什么函数?
生:一次函数.
师:如图2,在这个过程中,t与v又有怎样的关系?是我们学过的函数吗?
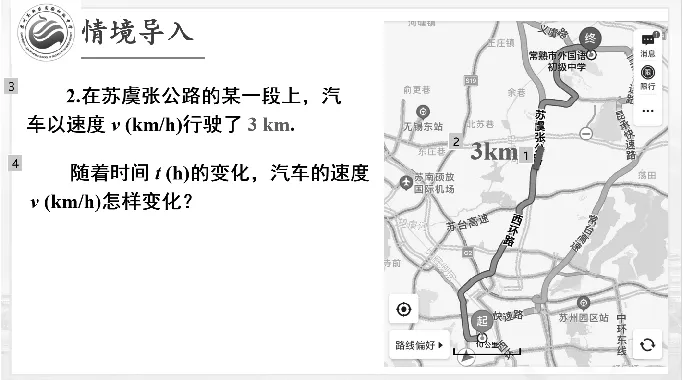
图2
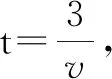
师:有一段下坡路,若不踩油门,随着时间的变化,汽车的速度会怎样变化?(学生沉默了半分钟.)
师:大家可以回想一下自己骑自行车下坡的体验,你感觉速度怎样变化?
生:速度越来越快.
师:可见,这不再是一个匀速运动.此时,路程与时间会是怎样的关系呢?为了探究这个问题,我们来做一个实验.
数学实验:播放小车沿斜面下滑的视频.
通过数学实验得到数据,如表1.

表1 实验数据
师:观察表1,你认为S是t的函数吗?是一次函数吗?是反比例函数吗?
生:S是t的函数,但既不是一次函数,也不是反比例函数.
师:请同学们画出这个函数的图象.(投影展示)
师:老师和大家一样也画出了图象,请看图3,这是我们熟悉的函数图象吗?
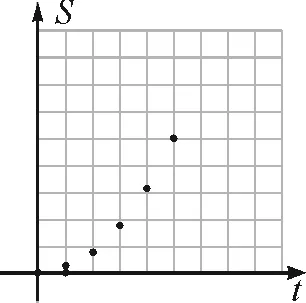
图3
生:不是.
师:这是一个新的函数.我们通常是怎样研究函数的?
生:研究函数的概念、图象、性质,运用函数知识解决实际问题……
师:概念通常又是怎么得到的?
生:从生活中实际问题抽象而来.
师:是的,生活中存在很多类似的函数关系……
设计意图:上课开始,教师就和学生分享了从自己学校到学生所在学校的路上的历程,拉近教师与学生的距离,将学生从数学课堂带入现实生活情境中,符合PBL模式中设计完整学习情境的理念.在这个情境中,学生体会到可以用数学语言来解释现实世界中的现象,发现在不同情境下,路程与时间、速度与时间的函数关系.通过已经学过的函数关系,回顾研究函数的一般思路,为本节课进一步研究新的函数奠定基础. 研究下坡路时路程与时间的函数关系,就是建模的过程,通过实验,由形入手,发现了一类新的函数.这是什么函数,它有什么特征,有什么作用?在问题的驱动下开始本章节的研究.
2.2 环节(二)——自主探究,合作交流
校园风景如画,老师带领同学们来到学校门口的水池旁,一起观察.
(1)水滴激起的波纹不断向外扩展,圆的面积 S 与半径 r 之间的函数关系为.
(2)学校在另一侧再建一个周长为20m的矩形水池,水池的面积S(单位:m2)与一边长 x(单位:m)之间的函数关系为.
(3) 如图4,外侧矩形长10m,宽3m,水池的边缘是等宽的,宽度为 xm,则中间小矩形的面积 y(单位:m2)与 x之间的函数关系为.
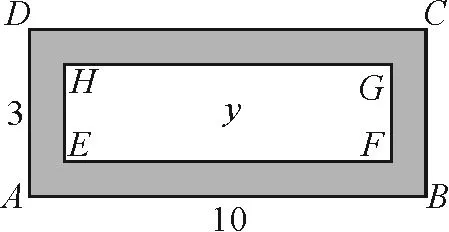
图4
问题1S=πr2,S=-x2+10x,y=4x2-26x+30三个表达式有什么共同特征?
归纳得到二次函数的概念:一般地,形如y=ax2+bx+c(a,b,c是常数,且a≠0)的函数叫做二次函数.其中x是自变量,y是x的函数.
学生讨论概括二次函数解析式的特征:(1)等号右边是关于自变量的整式;(2)最高次项的次数是2;(3)二次项系数不等于零.
问题2在以上实际问题中,自变量可以取哪些值?
归纳得到二次函数自变量的取值范围:
(1)通常二次函数y=ax2+bx+c(a≠0)的自变量x可以是任意实数.
(2)如果二次函数的自变量表示实际问题中的某个变量,那么它的取值范围受到实际意义的限制.
设计意图:在PBL模式的理念下,学生需要在一个真实的情境中对驱动问题展开探究.环节 (一)中,学生已经明确了要研究的问题,并对这个问题产生了浓厚的兴趣.环节(二)中,教师带领学生进入真实的校园场景,观察校门口的水池,探究水滴入水、水池面积等变化过程中变量之间的关系,发现这些变量之间的共同特征,从而归纳出新的函数——二次函数,并在此基础上展开研究.
2.3 环节(三)——动手操作,解决问题
小组活动:每人写一个二次函数,请同桌说出二次项系数、一次项系数和常数项.
例题如图5,学校在长300m,宽90m的矩形广场内修建等宽的十字形道路,设道路宽为 xm,绿地面积为ym2. 你能写出绿地面积与道路宽之间的函数表达式吗?道路宽的取值范围是什么?
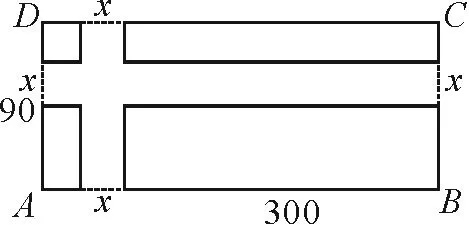
图5
探究如图6,用长50m的护栏围成一块靠墙的矩形花园,墙的长度是20m.请利用本节课所学知识,提出一个问题并解决,分小组完成.

图6
设计意图:学生通过环节(二)的探究得到一个“产品”(PBL模式的特征之一)——二次函数模型,环节(三)继续带领学生漫步校园,从教学楼前的花坛入手,学生以小组合作的形式,提出问题并解决问题,体现了PBL模式的项目式教学.在解决问题的过程中,学生可能需要用一元二次方程或二次函数的性质来解决问题,也可能需要思考方程、不等式与二次函数的关系,学生在思考、探索等过程中得到了必要的数学思维训练,体会到了数学思维的多元性,并且激发出后续研究二次函数性质的好奇心与求知欲.
3 基于PBL模式的课例赏析
3.1 基于问题情境展开学习
环节(一)为教师到学校路途中所遇之景,环节(二)为进校所见一景,环节(三)为教学楼前一角景观,整节课基于漫步校园所遇之景的变化,由学生自己提出问题,主动探索问题,围绕二次函数的概念这一主线展开学习.学生的学习体现了PBL模式的两个要点:
(1)学生是学习的主人
在PBL模式中,学生是学习的主人. 在本课的学习中,不再由教师讲授知识,而是学生自主探索.如环节(一),每个学生都可以根据自己的生活经验和学习状态多角度思考,从而得出不同程度的结论,学习积极性被调动起来了.环节(二),围绕校园里的水池,学生观察水滴入水的过程,思考扩建水池的设计,发现这些过程中变量的关系,提炼它们的共同特征,从而归纳得出一类新的函数——二次函数.
(2)在问题解决过程中获得新知识,发展新能力
环节(一),下坡路段上路程随时间变化的关系,学生由生活经验可知是函数但不是一次函数,问题有一定的难度,学生一时无法解决.通过数学实验,得出路程随时间变化的数据,再画出函数的图象,既可以让学生感受到函数的不同表现形式,感受数形结合,也充分发挥了学生的主体作用.环节(二)和环节(三),学生在探究过程中,不仅学习了二次函数这个新的知识,而且亲自参与建模过程,这些都体现了PBL模式的“在探究过程中学习及应用学科思想”.
3.2 基于问题的教学反思
教师的教学围绕PBL模式的三个要点展开:
(1)以激发求知欲和好奇心为支点
教育心理学的研究指出,好奇心是推动儿童和成人去获得新知识的主要动机.学生的求知欲和好奇心是课堂活力的源泉,是课堂教学价值的支点.如何激发学生的求知欲和好奇心呢?本课从学生熟悉的骑车上坡下坡问题入手,结合校园里的真实场景,让每个学生都有话可说,有法可想,培养了学生的发散思维.学生获得了成功的体验,学习积极性也被调动起来了.
(2)教师是辅助者和引导者
环节(三)原先的设计是由教师呈现一组题,学生练习,以题目增强二次函数的概念的巩固.但是PBL模式中,教师是指导学生认知学习技巧的教练,因此最终继续创设情境,放手让学生自主探索.再如环节(二),教师在学生归纳得出二次函数概念的基础上,结合实际问题,考虑自变量的取值范围,有利于培养学生思维的严谨性,体现了教师引导者的角色.
(3)真实的基于绩效的评价
课程标准提出,学习评价的主要目的是为了全面了解学生数学学习的过程和结果,评价要关注学生学习的结果,也要关注学习的过程.PBL模式中要求建立真实的基于绩效的评价.环节(一),遇到新函数教师没有避开不谈或者直接告知,而是通过数学实验,让学生亲自经历探索两个变量关系的过程,环节(三),互相提问,既利于调动学生学习积极性,也可以暴露学生思维的局限性,最后在教师的引导下共同归纳注意要点.
4 结论
PBL在国外已形成一套成熟的教学方法,学生通过规划和完成一系列任务,最终实现某个目标或者解决某个问题,这就是项目.学生为了成功地完成项目,必须整合自己的学科知识和生活经验,促进团队协作,最终对自己或他人的表现作出评价,这是PBL教学法的精髓[3].在国内,由于课程时间的限制,不能很好地实行项目教学,比如,本课的驱动问题还需后续研究二次函数的图象和性质才能解决,无法在一节课内完整体现.再如,数学实验部分,按照PBL理念应该让学生真正进入数学实验室,借助打点计时器,记录路程随时间变化的数据,再通过数据画出函数的图象,这样可以更真实地经历从实际问题中抽象函数模型的过程,感受研究函数的方法,但是时间所限,本节课老师采用课前做实验,录好视频在课堂上播放的方式,也是一种变通与尝试.
