单元类型及接触对贴边岔管受力特性的影响分析

伍鹤皋，李端正，石长征，黄 巍

(1. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072； 2. 中铁第四勘察设计院集团有限公司，武汉 430063)

0 前 言

钢岔管的结构型式主要有三梁岔管、内加强月牙肋岔管、贴边岔管、球形岔管和无梁岔管等。其中贴边岔管最适合于从主管中分出一条支管且呈不对称布置的情况，一般支管与主管的直径比小于0.5。贴边岔管按压力钢管开孔后孔周补强的工作原理，分别在主、支管相贯线两侧设补强板或曲梁结构，降低开孔处应力峰值[1]。这种岔管因岔管外形尺寸比较小，补强结构不干扰水流，水头损失得到改善，耗钢量比较少，制作安装比较方便，因此在中低水头引调水工程或水电站工程中比较常用[2]。

贴边岔管目前常用的计算方法主要有面积补偿法、圆环法以及有限元法。其中面积补偿法较为简略，只能估算出补强加固面积，无法得知补强加固后岔管的应力分布等情况，只能用于小型工程[3]；圆环法是一种根据美国垦务局用于曲梁式岔管的计算方法，能计算岔管上的最大应力值，但是不能了解结构整体受力状态；根据SL/T 281-2020《水利水电工程压力钢管设计规范》[4]，对于大型工程较为重要的贴边岔管，最好使用有限元法[5]进行复核计算。由于贴边岔管是组合薄壳结构，目前在贴边岔管进行有限元计算时，对于管道及主支管贴边大多直接采用板壳单元进行模拟分析，贴边部分与主支管分别采用不同的计算厚度，此方法的前提假定是贴边所有部分与主支管均焊接在一起即共节点，因此计算效果较好。但是实际中贴边岔管贴边与管壁是两层结构且只有边缘通过角焊缝焊接在一起，存在边缘焊缝破裂后贴边与主支管管壁错动的风险，因此有必要对贴边岔管加强方式、模拟方法以及受力特性进行进一步深入研究，使其更贴近实际情况。

目前有限元法已广泛应用于钢岔管研究，单元类型及网格尺寸会在一定程度上影响有限元分析结果，其中贴边岔管基本采用板壳单元进行建模，而基于实体单元贴边岔管有限元模型的研究则较少。因此，本文结合某引调水工程中的“T”型贴边岔管，基于板壳单元以及实体单元分别对贴边岔管建立模型，研究单元尺寸和类型对于贴边岔管有限元分析结果的影响，以及角焊缝高度对于贴边岔管受力特性的影响。

1 计算条件

某引调水工程主管直径6 400 mm，连通管直径3 000 mm，形成一个90°分岔角的“T”型岔管，由于支管直径与主管直径之比小于0.5，因此采用贴边岔管补强的形式。根据设计内水压力1.3 MPa，经过强度初估计算，主支管壁厚均为40 mm，均采用宽度1 000 mm、厚度22 mm的贴边补强。其布置见图1所示。

岔管拟采用Q355C钢材，弹性模量为2.06×105MPa，泊松比为0.3，重度为78.5 kN/m3，线膨胀系数为1.2×10-5/ ℃。根据SL/T 281-2020《水利水电工程压力钢管设计规范》[4]，正常运行工况下岔管钢材允许应力分别为整体膜应力164 MPa，局部应力262 MPa。

图1 “T”型贴边岔管布置 单位：mm

2 壳单元网格尺寸对贴边岔管受力特征的影响分析

网格划分是有限元分析计算重要的环节，其目的就是将整体模型离散成若干个小单元，然后通过积分的方式对模型进行求解。网格划分时网格尺寸不仅影响计算时间，同时对计算结果的可靠性也有影响。有限元计算中的网格单元划分尺寸小数量多可提高计算结果的精度，但运算时间较长;网格尺寸大数量少，虽然节约了计算时间，但结果往往达不到设计要求。贴边岔管是在主管管壁上开通一支管，并在主管及支管相贯线两侧进行贴边补强，由于其体型的复杂性，网格尺寸对整个模型的结果精度影响较大[6]。目前贴边岔管进行有限元分析时大多采用板壳单元建模，本节拟采用不同网格尺寸的壳单元进行建模，对其有限单元网格尺寸进行敏感性分析。

2.1 计算方案与模型

为研究贴边岔管壳单元在不同网格尺寸情况下，结构的受力特征变化规律，现定义网格尺度α=L/R(其中L为壳单元网格平均尺寸，R为贴边岔管主管半径即3.2 m)，网格平均尺寸分别采用0.50、0.40、0.30、0.20、0.10、0.05、0.03 m以及主支管相贯线附近最小网格尺寸0.0035 m其他部分网格平均尺寸0.20 m共8种方案，分别用A-1～A-8表示，其中A-8方案的有限元网格如图2所示，各方案网格尺度如表1所示。

表1 贴边岔管壳单元计算方案

2.2 贴边岔管应力随壳单元网格尺度的变化规律

对A-1～A-8方案有限元模型施加同样的约束与内水压力进行有限元计算之后，以如图3所示的贴边岔管主支管相贯线应力集中处A点出发，分别整理了各方案沿主、支管母线上的中面Mises应力变化曲线，如图4、5所示。

图2 A-8方案主支管及相贯线附近有限元网格

图3 A点为起点的应力路径

图4 主管母线路径应力变化曲线

图5 支管母线路径应力变化曲线

根据图4、5分析可知：当壳单元网格尺度a减小即整体网格变密时，贴边岔管相贯线处Mises应力整体呈现增大的趋势，说明基于壳单元的贴边岔管的Mises应力会随着网格尺寸的减小而增大。同时比较A-8与A-4两个方案的应力结果可以看出，A-8方案只是主支管相贯线处网格尺寸加密至0.0035 m而其他部位平均尺寸与A-8方案相同为0.2 m，但方案A-8的应力却比A-4增大了很多，说明贴边岔管的应力大小主要是相贯线附近的应力受网格尺寸影响明显，贴边岔管主支管相贯线附近的网格尺寸越小其Mises应力越大。

不同网格尺度方案以A点为起点的两条路径应力变化规律相似，A点应力值最大，随着距离相贯线越远，主支管Mises应力先迅速下降到应力最低值，之后有一段小幅增长，随后应力值基本保持稳定。说明贴边岔管补强板以外部分管壁受孔口应力集中影响较小，所以网格尺寸对主支管距离相贯线较远处的应力影响也较小。

当网格平均尺寸减小至方案A-6的0.05 m，即网格尺度减小至1.56%时，沿主支管母线的Mises应力分布曲线便基本趋于一致，应力随着网格尺度的继续降低而变化不大，但运算耗时成倍增加。这说明只要网格尺度达到约1.56%时，岔管应力即可满足设计精度要求。

2.3 贴边岔管变形特征

不同网格尺度a下各方案的岔管合位移如图6所示，最大合位移均对称出现在主管上靠近相贯线的两侧，各方案合位移分布特征基本一致，A-1、A-6方案最大合位移分别比A-8方案大1.32%和0.13%，说明贴边岔管最大位移受网格尺度影响很小。

图6 不同壳单元网格尺度方案岔管合位移 单位：m

3 基于实体单元的贴边岔管受力特性

实际工程中的贴边岔管其贴边补强板与管壁之间为接触关系，贴边补强板外缘通过一圈角焊缝与管壁焊接固定，主支管贴边连接处通过对接焊与主支管固定。本小节将从贴边岔管主支管贴边补强板外围角焊缝的高度着手，探究其对贴边岔管整体结构的影响。

3.1 计算方案与模型

钢岔管管壳、贴边以及焊缝网格全部采用ANSYS中的SOLID185八节点实体单元进行模拟。在主支管贴边补强板与主管和支管之间采用面-面接触库伦摩擦来模拟实际工程中的贴边岔管工作情况，接触采用ANSYS中的CONTA174单元进行模拟，其中摩擦系数按最不利情况考虑取0。

有限元模型建立在笛卡尔直角坐标系坐标(X，Y，Z)下，XOY面为水平面，竖直方向为Z轴，向上为正，坐标系成右手螺旋，坐标原点位于主管中心。在正常运行工况下，贴边岔管的有限元模型网格如图7所示，接触单元如图8所示。

图7 基于实体单元贴边岔管有限元模型

图8 主支管贴边接触单元

为了对贴边岔管主支管贴边补强板外围角焊缝高度进行敏感性分析，角焊缝高度分别取2/3h、1/2h、1/3h以及0h(即贴边外围与主支管管壁不焊接)4种方案(其中h为主支管贴边厚度)，焊缝截面为等腰直角三角形，分别用B-1、B-2、B-3、B-4表示，其中各方案中主管与支管贴边焊缝高度取相同值，同时假定一个全共节点方案用B-0表示。4种方案有限元模型只有主支管贴边外围角焊缝高度不同，其他部分包括接触关系均相同，其中B-1方案主支管贴边焊缝截面网格如图9所示。

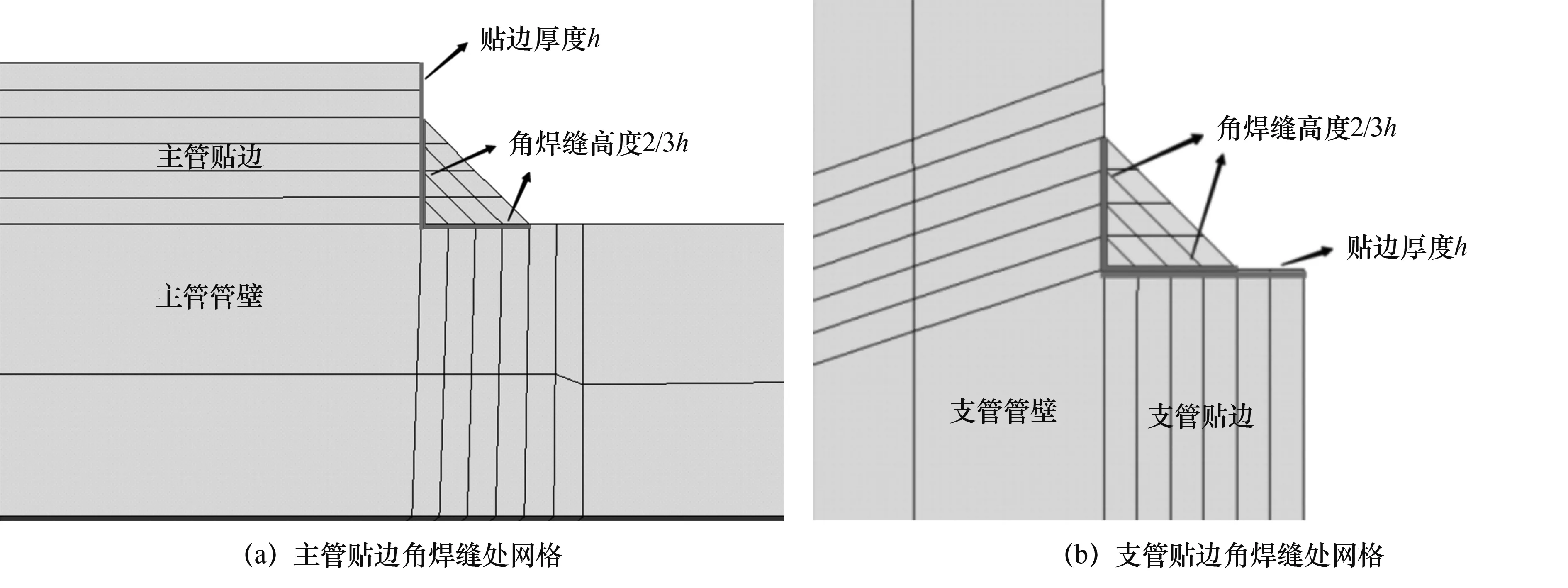
图9 B-1方案主支管贴边焊缝网格

3.2 贴边岔管应力

为便于分析，本文选定了如图10所示的两条应力分析路径。沿两条路径分别提取Mises应力、主管环向应力以及主管轴向应力，绘制应力变化曲线如图11、12所示，应力以拉为正，压为负，单位为MPa。

图10 应力分析路径

图11 S方向应力变化曲线

根据图11分析可知，各方案沿S路径应力变化曲线整体趋势基本一致，且B-1、B-2以及B-3方案沿S路径上的应力变化曲线基本重合，这说明角焊缝高度在减小到0之前的变化基本不会影响贴边岔管的受力情况；B-0方案中沿S路径方向的各应力变化曲线基本均处于最低位置，比4种建立接触的不同焊缝高度的实体单元贴边岔管方案小，这是由于B-0方案假定主支管贴边补强板与管壁全部共节点，不存在接触关系，导致其Mises应力均比建立接触的B-1至B-4方案更小。因此在同为实体单元模拟条件下，贴边与管壁设置接触的贴边岔管应力更大、更符合实际，应该考虑其接触条件。

B-4方案沿S路径的Mises应力在200 mm后均高于B-1～B-4方案，并且其沿S路径的环向应力与轴向应力也都最大，说明贴边外缘如果不与主管管壁焊接在一起或者说角焊缝破坏的情况下，会导致管壁整体的应力增大和受力不利。因此，在实际工程中保证贴边岔管贴边外缘角焊缝质量是非常必要的。

从图12可看出，无贴边外缘角焊缝的B-4方案沿θ路径的应力变化曲线与B-1、B-2、B-3三种有焊缝方案的变化曲线基本重合，说明贴边外缘的角焊缝高度对相贯线处的应力影响较小；Mises应力和环向应力均在0°与180°处最大，而在90°与270°处最小；轴向应力在45°、135°、225°以及315°处每隔90°呈周期性出现最大极值，但绝对值数值不大，不是贴边岔管的主要应力分量。

图12 θ方向应力线变化曲线

3.3 贴边角焊缝应力

有限元计算结果表明，角焊缝应力峰值位于图13(a)所示主管贴边角焊缝上B点。为研究贴边角焊缝应力随焊缝高度的变化规律，如图13(b)所示，以B点角焊缝截面O点为原点，沿管轴水平向为X轴，沿厚度竖直向为Y轴，整理B-1、B-2、B-3方案B点角焊缝截面Mises应力云图以及在X、Y方向上节点应力变化曲线如图14～17所示。

图13 贴边外缘角焊缝

由图14～17分析可知，B点角焊缝Mises应力在水平X方向逐渐增大而在竖直Y方向逐渐减小，最大Mises应力位于X方向最远点角焊缝外缘与管壁焊接处。在X与Y方向相同距离处，角焊缝高度越小时其Mises应力越大，主要是因为角焊缝高度较小时，角焊缝与管壁焊接的面积也较小，角焊缝同一位置处所受压强更大，使得角焊缝截面平均Mises应力水平相对更大，其与贴边及管壁脱离的可能性增大，因此实际工程中贴边岔管角焊缝高度不能过低；角焊缝高度越大时其体积也越大，稳固性更好，所承担的最大应力也更大，同时焊缝截面平均应力更小，因此角焊缝高度越大时相对更加安全。

图14 焊缝沿管壁节点Mises应力变化曲线 图15 焊缝沿管壁节点正应力变化曲线

图16 焊缝沿管壁节点X方向剪应力变化曲线 图17 焊缝沿管壁节点Y方向剪应力变化曲线

3种方案B点角焊缝X轴与Y轴上节点正应力均为正值，均受到拉应力，这是因为岔管受内水压时贴边与管壁会膨胀变形引起贴边角焊缝张拉，因此角焊缝截面法向应力主要为拉应力。角焊缝高度越小时，截面面积越小，因此最大正应力以及平均正应力越大，截面所受拉应力越大，角焊缝受力越危险。

3种方案B点角焊缝X轴与Y轴上节点X方向剪应力较大，且均为正值，均受到X轴正向较大的剪应力，分析是因为岔管受内水压膨胀变形时，主管贴边与管壁之间主要为沿接触面滑移的趋势，而竖向脱离的趋势较弱，因此角焊缝X方向剪应力较大，而Y方向剪应力较小；同时角焊缝高度越小，X方向剪应力越大，角焊缝所受剪应力越大，贴边与管壁脱离的可能性越大，角焊缝越容易与管壁脱离。

上述研究结果表明，贴边角焊缝高度越低时，其受力状态越不利，焊缝脱离的可能性也越大，因此实际工程中贴边岔管的贴边角焊缝高度不能过低，应保证贴边与管壁之间的焊接牢固性。

3.4 贴边岔管变形

图18、19为不同焊缝高度下贴边岔管位移云图及贴边截面变形情况。由图18、19可以看出，方案B-1、B-2以及B-3虽然贴边角焊缝焊缝高度不同但只要贴边与主支管管壁焊接，各方案位移分布规律就基本一致，受力变形也基本相同，而B-4方案由于贴边外缘未与主支管管壁焊接在一起或角焊缝破裂，将导致岔管变形时贴边外缘翘起而与主支管管壁面脱离，见图18(d)、19(d)，这种情况在实际工程中是绝对不能出现的，因此贴边岔管贴边外缘一定要与主支管管壁有良好的连接。

图18 贴边不同焊缝高度岔管合位移 单位： m

图19 不同焊缝高度贴边变形情况

4 结 论

本文从岔管受力与变形特征两个角度对壳单元网格尺寸进行敏感性分析，然后基于实体单元建立贴边岔管模型，研究贴边与管壁全共节点以及考虑接触的贴边岔管受力的差别，同时对贴边角焊缝高度进行敏感性分析，得出结论如下：

(1) 壳单元网格尺寸对贴边岔管主支管相贯线附近的应力大小有较大影响，当网格尺度减小至1.56%时，随网格尺度继续减小岔管应力趋于稳定，但贴边岔管位移分布规律及大小基本不受壳单元网格尺度的影响。

(2) 在模型尺寸、约束及荷载相同的情况下，采用壳单元与实体单元对贴边岔管的有限元计算结果会产生一定影响，基于实体单元且考虑管壁与贴边之间接触后，其计算精度较管壁与贴边采用全共节点实体单元有所提高，但基于壳单元的贴边岔管在网格划分达到一定网格尺度时，基本能满足设计精度要求，且效率更高，因此选择壳单元对贴边岔管进行有限元建模计算也是可行的。

(3) 贴边岔管采用实体单元建模且建立接触时，在贴边外缘有角焊缝的前提下，焊脚高度的改变基本不影响岔管整体应力及变形特征，但贴边角焊缝高度越低时，焊脚受力状态越不利，若贴边外缘与管壁不设置角焊缝或焊脚过低而开裂时会导致岔管受力时贴边与管壁部分脱离，变形增大。因此，选择贴边厚度的2/3作为贴边角焊缝的高度是基本合理的。