综合运用集中度与圆形分布法分析124例肾综合征出血热季节性分布特征

余晚凤，陶际春，范冬青，卜祥祥，孙恩涛，杨进孙，王文节

1.皖南医学院检验学院卫生检验与检疫学教研室，安徽 芜湖 241002 2.皖南医学院第一附属医院感染性疾病科

肾综合征出血热（hemorrhagic fever of renal syndrome,HFRS）又名流行性出血热，是由汉坦病毒引起的一种自然疫源性急性病毒性乙类传染病。我国是全球HFRS疫区分布最广、发病最多、危害最重的国家，累计报告病例数占全球病例总数的90%以上[1]。该病具有传播速度快、流行范围广、危害性大和突发性强等特点。近年来集中度和圆形分布法广泛用于媒介生物性传染病的季节性特征分析[2-4]。皖南地区是HFRS 流行地区，为了解当地HFRS 病患发病时间的季节性分布特征，同时验证上述两种方法在分析HFRS 流行特征中的应用价值，本研究对皖南医学院第一附属医院收治的

HFRS患者进行分析，现将结果报告如下。

1 材料与方法

1.1 一般资料 收集2010 年7 月—2020 年9 月期间在皖南医学院第一附属医院实验室诊断为HFRS的病例。纳入标准：①符合HFRS 诊断标准[5]；②患者基本信息保存完整、真实可靠。

1.2 研究方法

1.2.1 集中度 HFRS发病时间季节性的强弱可通过集中度的大小表示，具体计算公式如下[6]：

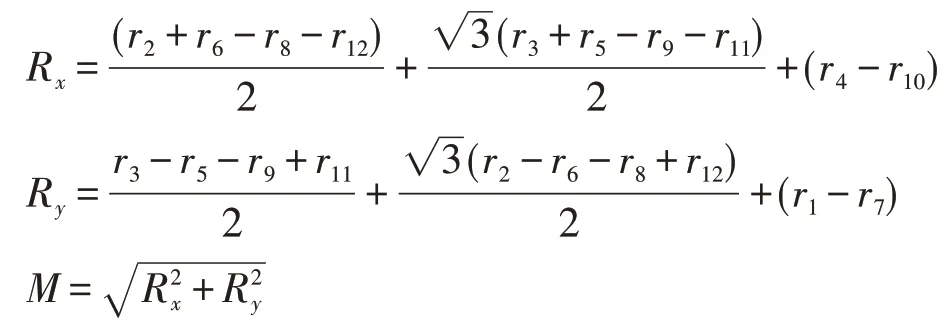
其中M为集中度，R为离散度，r为各月份HFRS发病数与全年总发病数之比。

当集中度M的取值范围为0～0.3、＞0.3～0.5、＞0.5～0.7、＞0.7～0.9、＞0.9～1 时，表示发病时间季节性强弱分别为季节性不明显或季节性较弱、有一定的季节性、有明显的季节性、有很强的季节性、有严格的季节性[6]。

1.2.2 圆形分布法 圆形分布相当于线性资料的正态分布，适用于单峰分布资料，其角度表示法与三角学上不同，是一组以查三角函数值为准，且具有周期性变化的数据转化为线性资料的统计方法[2]。通过观察 2010 年 7 月—2020 年 9 月 HFRS 患者入院接受诊疗的资料数据，流行呈非单峰型，参照有关文献[2]，根据患者发病时间趋势，将数据拆分为春夏季（3—8 月）和秋冬季（9 月—次年2 月）两部分进行季节性分析，具体分析步骤如下：

（1）春夏季（3—8 月）：以春夏季为一周期，一个周期为 360°，3—8 月共 184 天，故 1 天转化角度为1.957°（360°/184）。以 3 月 1 日 0 时为起点，以每月月中为组中值，故组中值折算为角度后，3 月对应30.334°（15.5×1.957°），4 月 对 应 90.022°（46×1.957°），以此类推。按照下列公式，计算出集中趋势值、平均角以及平均角标准差。

（2）秋冬季（9 月—次年2 月）：以秋冬季为一周期，9月1日0时为起点，9月—次年2月共181天，故1天对应角度为1.989°，计算方法如春夏季。

相关计算公式为：

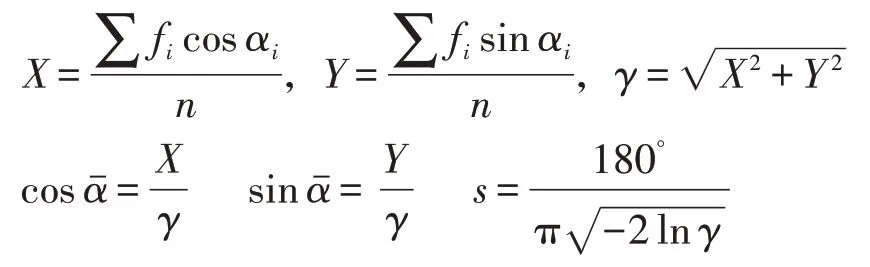
其中fi为月发病人数，α为组中值转换的角度，i为月份，γ为圆形分布的集中趋势，通常γ的值在0与1之间，为平均角，s为平均角的标准差，可通过（±s）推算发病高峰期。

（3）不同性别HFRS 病例组角均数比较：采用Watson-Williams检验。

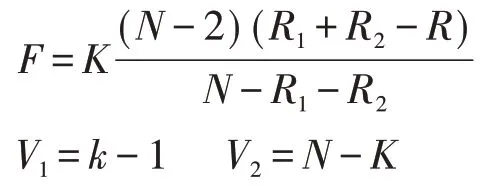
其中R1=n1γ1，R2=n2γ2，R=Nγ，K为校正因子，N为各样本例数之和，V1、V2为自由度。

1.3 统计学方法 应用SPSS 25.0 统计学软件进行数据分析，进行Watson-Williams检验，检验水准α=0.05；采用Excel 2016进行图表制作。

2 结 果

2.1 病例基本情况 共搜集病例149 例，排除资料不完整病例和输入性病例，符合纳入标准的病例共124 例，占总病例数的83.22%。124 名患者中，男女比例为4.64∶1，年龄中位数为49（40，60）岁。年龄最小者15岁，最大84岁。以15岁为一个年龄组，将调查对象分为 15～29 岁、30～44 岁、45～59 岁、60～74 岁和75 岁以上共5 个年龄组，各年龄组病例的构成比分别为 12.90%、24.19%、37.10%、23.39%、2.42%，其中30～59岁年龄段的病例数最多，占总病例数的61.29%。不同职业中，农民69 例，占55.65%；工人20 例，占 16.13%；无业人员 16 例，占12.90%；其他劳动者14 例，占11.29%；学生、干部等其他发病者占比最少，仅4.03%。

2.2 发病的季节趋势 根据2010—2020 年各月发病病例季节趋势图，发病高峰主要集中在4—7 月，其次是12月—次年1月。见图1。

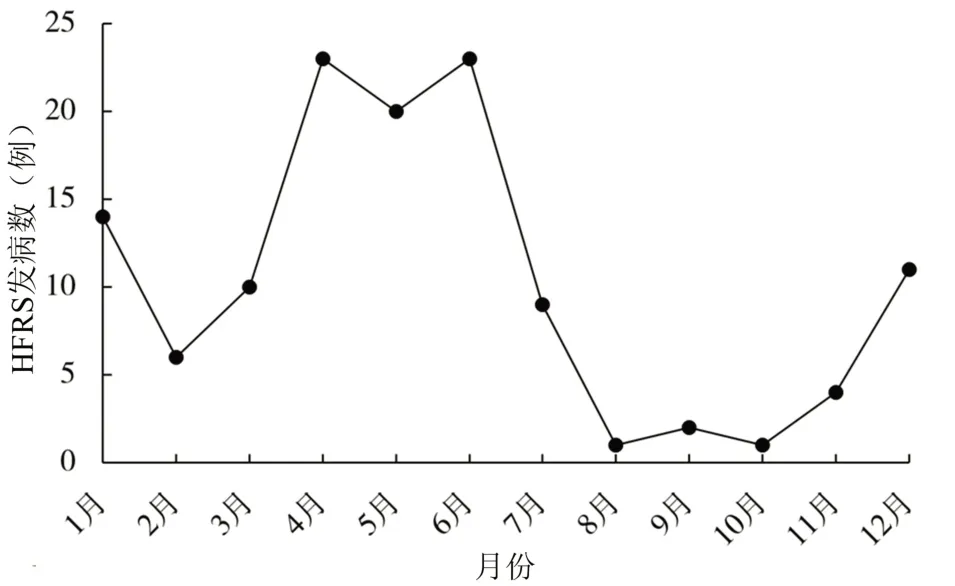
图1 2010—2020年HFRS各月份发病病例季节趋势图

2.3 集中度法 根据各月的HFRS 发病患者数和集中度计算公式，计算得到Rx=0.41，Ry=-0.04，M=0.42，M在 0.30～0.50 之间，表明 HFRS 患者发病时间具有一定的季节性。

2.4 圆形分布法 根据圆形分布法拆分分析结果，HFRS总病例春夏季（3—8月）集中趋势值γ为0.38，结合各组病例患者数，查圆形分布γ界值表得P＜0.001，说明存在，即HFRS患者发病时间具有集中趋势，对应发病高峰期为4月4日—6月25日。秋冬季（9 月—次年2 月）集中趋势γ为0.51，同理可得其发病高峰期为12 月3 日—次年2 月12 日。该法表明HFRS 患者发病时间分布呈双峰型，其中春夏季（3—8 月）高峰期为主高峰，秋冬季（9 月—次年2月）高峰期为次高峰。见表1。

表1 124例HFRS患者圆形分布法拆分分析结果

将两周期总病例拆分为男女两组，对比两组高峰日及高峰期结果差异。Watson-Williams 检验结果显示，两周期不同性别的季节高峰差异均无统计学意义。见表2。

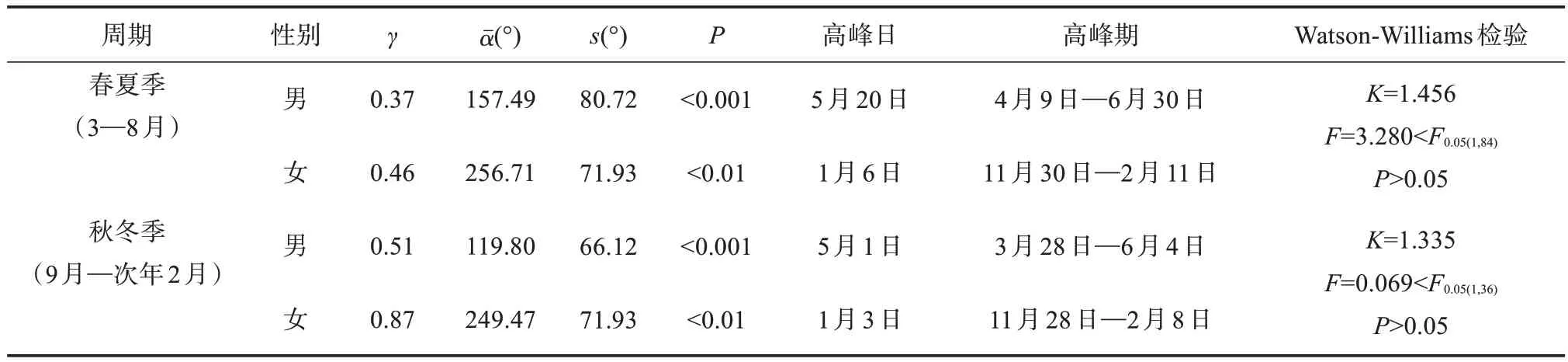
表2 124例HFRS不同性别患者圆形分布法拆分分析结果

3 讨 论

传统三间分布在进行疾病的季节性流行消长趋势分析时，常采用人群发病频数或发病率进行疾病流行曲线的绘制。该方法虽能直观显示疾病的季节分布特征，但仅能粗略地定性描述，不能进行假设检验。这使得疾病的季节性流行消长趋势曲线的高峰鉴定可能受到随机误差的影响[2,7-8]。而将集中度和圆形分布法同季节性流行趋势图联合使用时，可在判定季节性强弱的同时，定量且精确地计算其实际发病的高峰日及高峰区间，从而全面掌握疾病的季节性流行趋势特征[9]。其中集中度适用于定性判断疾病季节性强弱，简单易操作；圆形分布法适用于推算疾病发病高峰日及发病高峰区间，可在精确定量计算的同时得到具有统计学意义的高峰日及高峰期结果，与集中度相互补充，两种方法均不易受采集时间的影响[6,10-13]。目前集中度和圆形分布法的综合分析，常用于传染病季节分布特征分析和急性事件暴发规律分析[14]。

集中度法和圆形分布法综合分析结果显示，该院 2010—2020 年 HFRS 发病的集中度M=0.42，提示HFRS 患者发病时间具有一定的季节性；HFRS 病例发病的实际季节分布特征为主-次高峰型的双峰分布，主高峰期为4 月4 日—6 月25 日，次高峰期为12月3 日—次年2 月12 日，发病季节主要集中于5 月和1 月，符合姬鼠型疫区发病特点[15-16]，与孙燕群[17]等研究的HFRS 疫情分布特征接近，但与宇应涛[10]等关于次高峰处的特征有所不同，造成这种情况的原因可能是在使用圆形分布法描述疾病流行特征时未对原始数据进行非季节因素分解。

通过观察两周期HFRS 不同性别高峰期分布情况可知，女性较男性病例的发病高峰期更集中，可能与女性较男性暴露途径少有关，尤其是30～59岁男性农民，作为家庭主要劳动力，从事水稻、茶叶等不同农作物的种植，接触鼠类及其排泄物的机会增加[18]。同时，HFRS 疫情分布除受接触途径及人群易感性影响外，还受温度、湿度、降雨量等气候条件影响[18]，Watson-Williams 检验分析 HFRS 不同性别两周期的季节高峰差异均无统计学意义，提示不同性别的季节高峰期分布可能受气象及植被覆盖率等因素影响较大。

值得注意的是，圆形分布法仅适用单峰分布资料，若用于未进行周期分解的多峰分布资料，则可能会掩盖或低估计算所得的发病高峰日及其区间结果的统计学意义[13]；同时在选取时间单位时，跨度不宜过大，否则会低估集中程度分析结果的精度，降低其流行病学意义。因此，为准确掌握HFRS 季节性消长趋势特征，建议联合运用集中度和圆形分布法，定量计算出HFRS 患者发病高峰日及高峰区间，与HFRS 潜伏期综合分析，推断出HFRS 的感染高峰期，从而为该地区的疾病预警和控制提供有力的依据。