改进哈里斯鹰优化算法求解作业车间调度问题*
2022-11-25李云秋熊瑞平温记明
李云秋,熊瑞平,温记明,苏 俊,谭 平
(四川大学机械工程学院,成都 610065)
0 引言
在智能制造的发展背景下,结合数字化、网络化、智能化制造技术和装备的柔性数字化生产线、数字制造车间、智能工厂等逐渐成为制造业的焦点话题。其中作业车间调度问题(Job-Shop scheduling problem,JSP)作为加快智能生产车间产品加工的核心问题得到广泛的研究。作为智能优化算法应用领域之一的JSP是著名的NP-hard问题,在智能算法的优化计算下产生了多种调度方法,优化了多品种批量化作业车间的生产结构或资源配置。柳青红等[1]在遗传算法的交叉过程中引入禁忌搜索算法对JSP进行求解,提高算法全局寻优能力;闫旭等[2]将鲸鱼优化算法与量子计算结合以求解JSP,提高算法全局搜索能力和收敛精度,有效地改善了求解JSP的结果。姚远远等[3]通过对灰狼优化算法进行了进化种群动态、反向学习初始化种群以及最优个体变异的改进操作,求解JSP获得了比较好的调度方案。虽然上述算法获得了相对较优的方案,但是在寻优效率和求解能力上仍有一定的不足,寻找更好的算法用于求解JSP问题提高调度的效率获得更优的调度方案,依然是值得关注的问题。
哈里斯鹰优化算法是由AAHA等[4]提出的一种新型群智能算法。目前哈里斯鹰算法被广泛应用到TDOA定位[5]、医学图像分割[6]、钢筋混凝土剪力墙的抗剪强度[7]、低维和高维的特征选择[8]等领域。哈里斯鹰优化算法具有调节参数少、较强全局搜索能力的优点,但在算法勘探和开发过程中,易陷入局部最优且寻优精度低。
针对上述哈里斯鹰算法存在的问题,提出了一种改进哈里斯鹰优化算法(improved harris hawks optimization,IHHO),并将其应用到求解作业车间调度问题上。引入了一种变邻域搜索算法,针对JSP的特点设计了两种邻域结构,用于寻找最优个体的邻域更优解;对算法的更新策略作出了改进,在种群个体中引入了一种自适应逐维柯西高斯变异策略,平衡了全局搜索和局部开发的能力;对最优个体采用了逐维均匀高斯策略进行扰动,并使用了贪婪算法获取最优解,引导种群个体向最优方向移动。最后,将改进后的算法对11个作业车间调度领域的标准算例进行了实验,验证了算法的有效性。
1 问题描述及模型
作业车间调度问题可以描述为:同一个工件的加工顺序以及相应加工机器和加工时间都是确定的,不同工件的同一道工序使用的机器可能是不同的,调度的目的就是安排各个工件的各个工序在机器上的加工顺序,使得所有工件加工完成的最大完成时间最小。在加工过程中,JSP需要满足的需要条件有:
(1)同一个机器在一个时间段里只能加工一个工件的工序;
(2)同一个工件在同一时间段里只能在一个机器上加工,同一个工件按照工序顺序进行加工;
(3)一个工件的工序开始加工后,不能停止;
(4)机器均从零时刻开始工作;
(5)机器运行处于正常状态,过程中无故障。
以最小化最大完成时间为目标函数,n个工件,m台机器的作业车间,sik和cik表示工件i在机器k上的加工时间和完工时间,其中i,j=1,2,…,n;h,k=1,2,…,m,M表示一个足够大的正数。aihk=0,1;aihk=0表示工件i先在机器k上加工再在机器h上加工,aihk=1表示机器h先于机器k加工工件i。xijk=0,1;xijk=0表示工件i先于工件j在机器k上加工,xijk=1则表示工件j先于工件i在机器k上加工。利用整数规划模型进行表示,其表现形式为:
(1)
其约束条件:
cik-sik+M(1-aihk)≥cih
(2)
cjk-cik+M(1-xijk)≥sjk
(3)
cik≥0
(4)
2 改进哈里斯鹰优化算法
2.1 哈里斯鹰算法
哈里斯鹰算法[4]的主要思想是来自哈里斯鹰协同合作捕捉逃跑猎物的过程,该过程分为全局勘探和局部开发两个阶段。在哈里斯鹰追捕猎物过程中,随着迭代次数的增加,猎物的逃逸能量E逐渐降低,猎物的逃逸能量|E|≥1处于全局探索阶段,|E|<1进入局部开发阶段。
全局勘探阶段:哈里斯鹰随机分布在搜索空间[lb,ub]内,观察周围的环境,凭借其优越的视力采用两种搜索策略尽可能地探索空间中的区域寻找猎物,根据概率q来选择鹰的位置更新策略。局部开发阶段:哈里斯鹰开始逐渐地在猎物周围活动,形成包围趋势,根据|E|和随机变量r以及哈里斯鹰的追逐策略,对猎物采取四种围攻策略。
2.2 编码方式
本文采用基于工序的编码方式,利用ROV(ranked order value)规则,合理有效的编码会将哈里斯鹰算法中个体位置与车间工序编码相对应。工序编码的长度由每个工件的工序数之和决定,编码内容由工件号组成,首先制定工序编码规则,假设有3个工件,每个工件有3道工序,3个机器,则工序编码设定为[1,1,1,2,2,2,3,3,3]。工序编码含义为:第一个1表示第一工件的第一道工序,第二个1表示第一个工件的第二道工序,第一个2表示第二个工件的第一道工序。种群中哈里斯鹰个体的位置表示为x=[x1,x2,…,xd],d等于每个工件的工序数之和。假设有个体位置x=[0.2,0.5,0.9,0.1,0.6,0.3,0.8,0.4,0.7],将0.2,0.5,0.9,0.1,0.6,0.3,0.8,0.4,0.7按照从左到右的顺序编号,然后将x升序排列,再将升序后的位置x1一对应工序编码[1,1,1,2,2,2,3,3,3],最后再将x1转换回x,最后得到基于位置的工序编码。则编码转换方案如图1所示。

图1 编码转换方案示例图
图中,[0.2,0.5,0.9,0.1,0.6,0.3,0.8,0.4,0.7]是哈里斯鹰候选解,[1,2,3,4,5,6,7,8,9]是哈里斯鹰候选解的排序编号,[1,2,3,1,2,1,3,2,3]是哈里斯鹰候选解转换为调度方案的工序编码。
2.3 变邻域搜索
为提高哈里斯鹰算法的局部搜索能力,引入变邻域搜索算法[9],更细致深入地搜索最优个体的周围空间。根据设计的两个邻域结构,在算法进行全局或局部搜索之后,对最优个体依次执行插入和两次交换操作,直到达到设定的迭代次数或者获得符合邻域结构要求且优于当前解的邻域解,本文的设计两种邻域结构为:
邻域结构1:最优个体的位置由d个维度构成,首先随机选取最优个体中的一个维度,再判断这个维度的位置是处于个体位置编码的前半部分或是后半部分,如果是前半部分,则将抽取出的维度值移到个体位置编码的最末尾,如果是后半部分,则将抽取出的维度值移到个体位置编码的最前端。如图2所示,个体维度值0.9在前半部分,所以将其移到编码最末尾。

图2 邻域结构1示例图
邻域结构2:首先先将哈里斯鹰位置编码转换为工件工序的编码。然后随机选取一个位置1,再随机选择一个位置2,如果位置1和位置2对应的维度的工件号相同,则重新选取位置2,最后交换位置1与位置2上的维度值。通过设置位置1与位置2交换的工件号不同,可以减少算法做无用的邻域交换操作,从而增加得到更优解的几率。如图3所示,位置1选中一个维度上的工件2之后,位置2只能选择其他维度的工件1和3,然后再执行交换操作。

图3 邻域结构2示例图
2.4 逐维柯西高斯变异策略
在算法运行过程中,当前种群中的最优个体产生停滞更新现象,即猎物位置多次(设置为4次)没有改进时,采用逐维柯西高斯变异策略[10]和自适应权重系数随机扰动种群中至多一半的哈里斯鹰个体,使部分种群个体以远离最优解的方式更新位置,在设置的空间内扩大了搜索范围,产生了新解的可能性,增加了探索全局空间的多样性。利用式子j=randi([1,N])在种群X中随机选取出个体X(j),一共进行N/2次选择,N=种群规模。将选出的个体位置的每一个维度都按照式(5)执行变异操作。
设搜索空间有d维,将选取出的当前解X(j)=(X(j)1,X(j)2,…,X(j)d)经过逐维变异之后得到新的解Xnew(j)=(Xnew(j)1,Xnew(j)2,…,Xnew(j)d),逐维变异公式为:
Xnew(j)d=X(j)d×(1+ρ1×Cauchy(0,1)+ρ2×Gauss(0,1))
(5)
(6)
(7)
式中,Xnew(j)为个体变异后的位置;Xnew(j)d为个体位置的每一个维度值,随着迭代次数的增加;ρ1逐渐减小,柯西变异扰动的影响减小;ρ2逐渐增加,高斯变异对公式的影响增大,自适应参数的应用分别展现了柯西分布和高斯分布的优点,平衡了算法全局勘探和局部搜索的能力。
2.5 逐维自适应变异策略
算法产生最优解时,对当前全局最优个体进行逐维扰动,即扰动个体的每一个维度,提高获取到更优解的可能性和几率,通过使用式(8)的均匀高斯变异式以改变猎物(最优解)的位置:
Xrabbit_new(i)=Xrabbit(i)×(φ1×rand(1)+φ2×randn(1))
(8)
(9)
(10)
式中,Xrabbit为最优个体位置;Xrabbit_new为最优个体变异后的位置;Xrabbit_new(i)为最优个体的每一个维度值;φ1、φ2为随t变化的自适应动态调整参数。迭代前期,均匀分布的随机数处于主导地位,算法更多地搜索空间,后期高斯分布随机数的系数φ2逐渐增大,则更有利于提高收敛精度和局部寻优能力。为了更好地引导哈里斯鹰向猎物位置方向更新位置,使用贪婪算法选择最优个体是添加变异扰动后的新解或原解。
(11)
2.6 改进哈里斯鹰优化算法流程图
改进哈里斯鹰优化算法的流程图如图4所示,其具体步骤为:

图4 改进哈里斯鹰优化算法流程
步骤1:设置搜索空间范围,随机初始化种群个体;
步骤2:计算种群中哈里斯鹰个体的适应度,将适应度最优的哈里斯鹰位置作为猎物的位置;
步骤3:根据猎物逃逸能量E和随机变量r的大小采用对应的更新策略对每个哈里斯鹰个体进行位置更新;
步骤4:对种群中的最优个体执行变邻域搜索操作;
步骤5:对比4次迭代最优个体的适应度值,如果最优解未改变,则利用逐维柯西高斯变异策略随机扰动种群中至多一半的个体,引入新解,如果最优解改变,则直接执行步骤6;
步骤6:利用逐维自适应变异策略扰动最优个体的位置,对比扰动前后的适应度值,通过贪婪算法选择最优解,更新最优解和种群个体;
步骤7:在最大迭代次数内,重复步骤2~步骤6。
步骤8:输出最优解。
3 仿真实验
3.1 仿真条件
为验证IHHO算法的全局寻优性能并保证实验的可比性与公平性,所有算法均设置为种群规模N=30,迭代次数T=500,每个标准算例运行次数为30次。
3.2 IHHO与其他算法在基准测试函数上的对比
实验选取了哈里斯鹰算法[4]、灰狼优化算法[11]、鲸鱼优化算法[12]与改进哈里斯鹰算法在8个基准测试函数的平均值和标准差两方面进行对比,其中F1~F4为单峰基准测试函数,F5~F8为多峰基准测试函数,基准测试函数的具体函数信息如表1所示,实验结果如表2所示。

表1 IHHO在测试函数上关于平均值和标准差的实验结果

表2 测试函数具体信息
通过表2数据可以看出,IHHO在F1、F6和F8测试函数上取得了最优解,平均值和寻优标准差均为0,寻优成功率达到了100%,结果稳定。对于单峰函数,IHHO在F1~F4函数的寻优精度比HHO算法高上百个数量级,改进后的算法的收敛精度有大幅度地提高。对于多峰函数,在F5测试函数上的IHHO的寻优精度略高于另外三种算法;IHHO和HHO在F6和F8函数上的寻优结果优于其他对比算法,均取得了最优解;IHHO和HHO在F7测试函数上平均值相同,但IHHO的寻优稳定性比HHO强。综合来看,针对这8个算法测试函数的平均值和标准差而言,IHHO的寻优性能是最好的。
3.3 求解作业车间调度问题
针对作业车间调度问题,实验选取了HHO、GWO[3]、WOA[2]和IHHO算法在最小值、平均值和寻优成功率3个方面对比,FT类中3个标准算例和LA类中8个标准算例被用于这次求解JSP算法的性能测试和比较实验,得到了表3和表4的实验结果。同时分析表3和表4的每个算例数据得出,改进后的IHHO算法的最小值、平均值和寻优成功率的实验结果都是优于HHO、WOA和GWO的。

表3 改进哈里斯鹰算法与鲸鱼优化算法与灰狼优化算法的对比
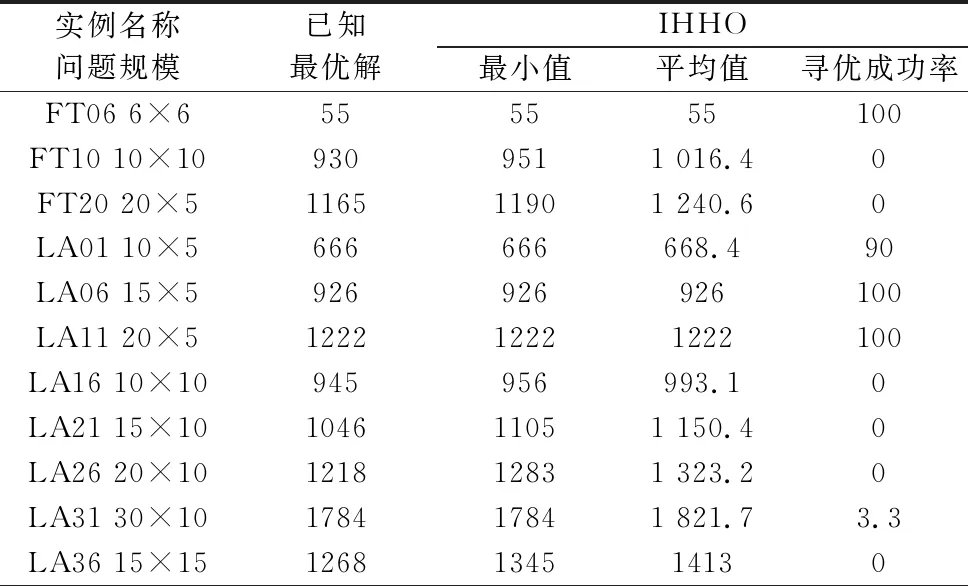
表4 改进哈里斯鹰算法与基本哈里斯鹰算法的对比
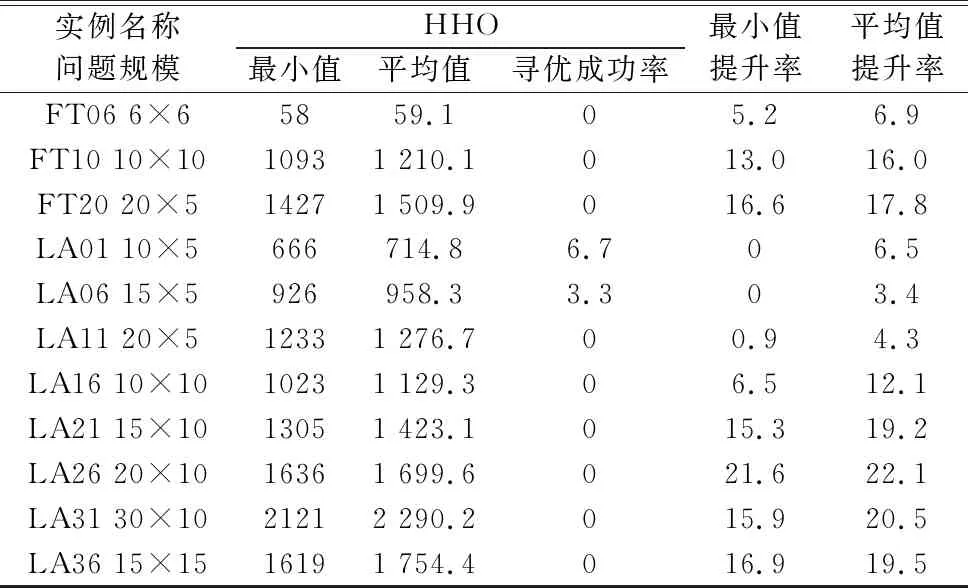
续表
由表4的数据可看出,IHHO在FT06、LA06、LA11算例上都达到了100%的寻优成功率;在LA01和LA31算例上也收敛到了目前已知的最优解,寻优成功率分别为90%和3.3%,其中,IHHO在LA31算例上的寻优最小值和平均值提升率分别为15.9%和20.5%。相对于HHO,IHHO在FT10问题上最小值和平均值分别提高了13.0%和16.0%;对于FT20实例最小值和平均值提升效果分别为16.6%和17.8%;在LA21实例上最小值和平均值提升率分别为15.3%和19.2%;在LA26实例上最小值和平均值提升率分别为21.6%和22.1%;对于LA36问题最小值和平均值的提升效果分别为16.9%和19.5%。综上所述,表明对哈里斯鹰算法的改进是有效的。
为了更直观地看出算法的收敛效果和寻优有效性,图5给出了部分实例的收敛曲线,分别是IHHO、HHO、GWO和WOA关于实例FT10、FT20、LA16、LA26、LA31和LA36的对比寻优曲线图。

(a) FT10 (b) FT20
可以看出,IHHO相对于其他算法在标准算例中的最大完工时间是最少的,在LA31实例的示例图中最大完工时间收敛到了最优解,IHHO收敛结果更好且收敛能力也比较强。改进之后的IHHO跳出局部最优和全局寻优能力都有了很大幅度的提升。
4 结束语
在求解作业车间调度问题过程中发现HHO算法具有收敛精度差,易陷入局部最优的缺点,因此提出了一种改进哈里斯鹰算法,引入基于变邻域搜索算法、对种群改进的自适应柯西高斯变异策略以及均匀高斯扰动策略的途径对算法进行改进与优化,并通过8个基准测试函数和11个JSP领域的标准实例进行实验,与其他元启发式算法GWO、WOA与基本的HHO算法进行对比,作业车间调度问题的仿真结果和收敛曲线表明,IHHO算法的有效性和相对的全局寻优能力,缩短了最大完工时间,得到了比较好的车间调度方案。在接下来的研究工作中,会对哈里斯鹰算法在多目标柔性作业车间调度领域的最优解进行针对性分析研究。
