基于贪心算法的双盘异步磨床砂轮动平衡策略

孙荣坤，胡王平，周裕康，张志新

(浙江大学能源工程学院，杭州 310000)

0 引言

磨床是一种重要的精加工设备，砂轮不平衡引起的振动会严重影响磨床的磨削质量，引起砂轮不平衡的主要因素有：砂轮颗粒系分布不均、安装砂轮的主轴存在剩余不平衡、砂轮安装误差导致的偏心、附着在砂轮上的冷却液不均匀。上述不平衡因素伴随着整个磨削过程，砂轮的不平衡状态不断在发生变化，因此通过常规离线式动平衡仪实现“一次平衡，长期使用”的方法对高精度磨床显然是不行的。

对于高速旋转系统，可通过球式、摆锤式、环装液体式被动自动平衡系统[1-2]实现无额外能量输入的自动平衡，但其结构复杂，在低于临界转速时会加剧不平衡，影响磨床磨削精度，因此不适用于磨床系统。随着磨削精度地不断提高，砂轮在线自动平衡系统应运而生，该系统可实现磨床运行全程监测，并根据一定的自动控制策略自动补偿不平衡量。磨床砂轮自动平衡系统的两个核心为动平衡执行结构以及自动平衡算法，磨床用动平衡头主要有机械式、喷液式、电磁式等[3-4]；其中机械式、喷液式动平衡头由于结构可靠、控制简单在精密磨床上得到了广泛应用；而动平衡算法经过多年的发展，出现了不少可用的动平衡算法。

经典的自动平衡策略有影响系数法自动平衡法[5]及其改进策略，如极小化最大残余振动的MINMAX影响系数法[6]、摄动影响系数法[7]、基于岭估计的影响系数法[8]、基于遗传算法优化的影响系数法[9]等，影响系数法具有平衡速度快，精度高的优点；但该方法需要采集振动相位，对于出厂前未预埋霍尔元件的磨床，只能贴反光纸通过光电器件获取键相信号，进而测得相位，而反光纸易被冷却液腐蚀，导致该方法难以长周期运行；该方法还需对平衡盘转动角度精确控制，需采用步进或伺服电机，这样会大大增加动平衡头的轴向尺寸，甚至改变磨床的振动特性。坐标轮换法[10-11]则仅需要测定轴承处的振动大小，具有信号采集容易、无需精确控制平衡盘相位，更适应简单紧凑结构的特点；但坐标轮换法在有高精度需求时，须保证两平衡质量严格同步旋转，这在结构简单紧凑的磨床砂轮平衡头上很难实现，且坐标轮换寻优分为相位寻优和幅值寻优两步，两步寻优的误差互相叠加更进一步影响了平衡的最终精度。滑膜变结构平衡算法[12]属非线性控制，具有平衡精度高，鲁棒性好的特点，但在滑膜面附近存在“抖振”现象，易引起执行器不必要的磨损以及发热。粒子群算法[13]以及遗传算法[14-15]等属智能控制算法，具有鲁棒性好，不易陷入局部最优的特点，但存在计算量大，实时性稍差的问题，不适用于磨床砂轮动平衡。

针对上述不足，提出一种硬件要求低、平衡精度高、平衡速度快的基于贪心算法的双盘异步动平衡策略，以满足开发低成本高精度的磨床砂轮在线动平衡系统的需要。

1 自动平衡原理

动平衡头是磨床在线自动平衡系统的执行机构，国内外多个研究机构[16-20]对此进行了研究，目前主要有机械式、喷液式、电磁式等多种平衡头，如图1所示。但其本质上还是利用两个或两个以上的等效偏心质量相等的旋转来校正磨床的不平衡量，动平衡过程原理如图2所示，其中m为系统等效偏心质量，ma、mb为两平衡盘的等效偏心质量，设ma=mb=M，三者的相位分别为φa、φb、φ。

(a) 机械式外部平衡头 (b) 机械式内部平衡头

图2 动平衡原理图

则总体不平衡量mt为：

mt=M·eiφa+M·eiφb+m·eiφ

(1)

令系统原有不平衡量的相位固定于直角坐标系的y轴负半轴，两平衡盘的相对位置任意转动，则总体不平衡量幅值|mt|满足以下关系式：

(2)

2 基于贪心算法的双盘异步动平衡策略

2.1 贪心算法简介

贪心算法[21]是求解最优化问题的重要方法之一，该算法将复杂最优化问题分解成规模较小的子问题，并求解子问题的局部最优解，最后组合全部的局部最优解得出全局最优解。贪心算法的基本过程为：①建立数学模型来描述问题；②把求解的问题分成若干个子问题；③对每个子问题求解，得到子问题的局部最优解；④把子问题的解局部最优解合成原来问题的全局最优解。

2.2 基于贪心算法的双盘异步寻优策略设计

2.2.1 双盘异步动平衡贪心算法数学模型

自动平衡寻优过程本质上是在一定的约束条件下，以总体不平衡量最小为目标的最优化问题，该过程的可以用数学模型描述为：

(3)

式中，φi为第i个独立的等效平衡质量块的相位列向量；φij为第i个独立的等效平衡质量块在j时刻所处的相位；gm(x)、hn(x)为平衡过程的约束函数；f(φ1,φ2,…,φi)为在约束条件下的最优化目标函数。

而贪心算法是求解该类问题的有效方法之一，在满足无“后效性”条件下，或在通过正确性证明的前提下，具备找到全局最优解的条件，可有效避免陷入局部最优解，最终实现完全平衡。

2.2.2 贪心算法子问题分解

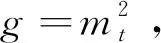
(4)

M[1-sin(α-β)]=m·sinα

(5)

从上式可以得出，第一次单盘异步寻优的局部最优解是以固定盘相位为边界条件的局部最优解，可以显式的表示为：

(6)

第一次寻优的停止位置实际上是在固定B盘所处的相位下的以总不平衡量最小为目标的局部最优解，接下来应固定A盘，寻找下一个新的局部最优解，该过程的数学描述为：

(7)

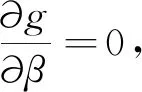
M[1+sin(α-β)]=m·cosβ

(8)

该解实际上是在上一次寻优结束的基础上，以不平衡量最小为目标的局部最优解，根据贪心算法思想，需要多次交替异步迭代，根据式(5)和式(8)可得基于贪心算法的双盘异步寻优过程的最优解递推方程组：

(9)

2.2.3 贪心算法正确性证明

贪心算法不是对所有问题都能得到整体最优解，首先选择的贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。其次，贪心算法最终能否找到全局最优解的关键就是能否通过正确性的证明，常用的方法有归纳法和交换论证法，这里用数学归纳法进行证明：

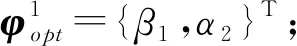
假设第k步时，贪心算法全局最优解存在，则根据式(9)可知，第k步的全局最优列向量为：

(10)

那么在第(k+1)步时，根据式(9)可得：

(11)

从中可解出βk+1、αk+2，两者组成第k+1步的全局最优解向量为：

(12)

根据式(10)和式(12)可知，在k+1步，贪心算法依然能够找到全局最优解，因此，在k∈N*时，贪心算法均能找到全局最优解。综上所述，基于贪心算法的双盘异步寻优算法能够通过正确性证明。根据贪心算法的性质可知，在通过正确性证明前提下，全局最优解αopt、βopt必存在于A、B盘异步迭代局部最优解的全集Φ*中，即：

(13)

式中，αopt、βopt是以{mt|minmt=M·eiφa+M·eiφb+m·eiφ}为目标的全局最优解，即两平衡盘合成不平衡量与被平衡对象的原有不平衡量等大反相，此时被平衡对象达到完全平衡状态。

2.2.4 双盘异步寻优策略程序框图

根据以上分析，可以归纳出基于贪心算法的双盘异步动平衡策略，式(4)和式(9)多次反复迭代的过程实际上是两偏心质量多粗异步转动寻优的过程。依据贪心思想，单次异步寻优，偏心盘相位转动至振动局部最优相位即可，在满足无后效性前提下，所有局部最优的组合即为全局最优，则整个寻优策略的程序框图如图3所示。

图3 双盘异步动平衡策略程序框图

3 基于贪心算法的双盘异步寻优策略的数值模拟

动平衡头的平衡能力与平衡精度，跟平衡盘质量与砂轮实际平衡量之比密切相关，存在一个最佳的匹配比，根据Schmmit公司SBS系列动平衡头产品手册给出的选型建议，平衡盘质量与被平衡砂轮的适宜质量比一般控制在1～3.3之间。以此为依据，利用MATLAB对基于贪心算法的双盘异步寻优策略进行数值模拟分析，令A、B平衡盘的质量为被平衡对象偏心质量的2倍，具体模拟实验参数如表1所示。

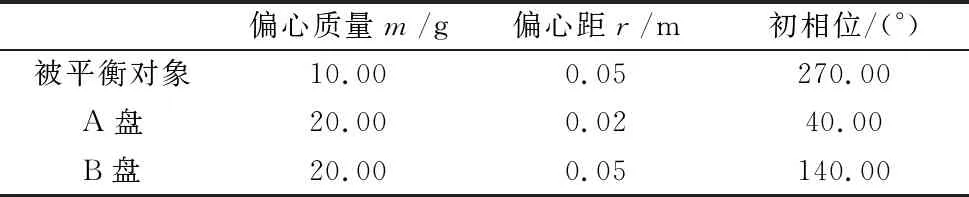
表1 数值模拟实验参数表

基于以上实验参数，用MATLAB仿真基于贪心算法的双盘异步寻优全过程，其结果如图4所示。

从图4中可以得出，自动平衡开始后，两平衡盘与被平衡对象的总不平衡量快速下降，表明本策略具有对恶劣工况快速调节的特点；在步进次数为23步左右时，总体不平衡量开始出现震荡，总体趋势为震荡下降，最终在47步进次数处实现了几乎完全平衡。

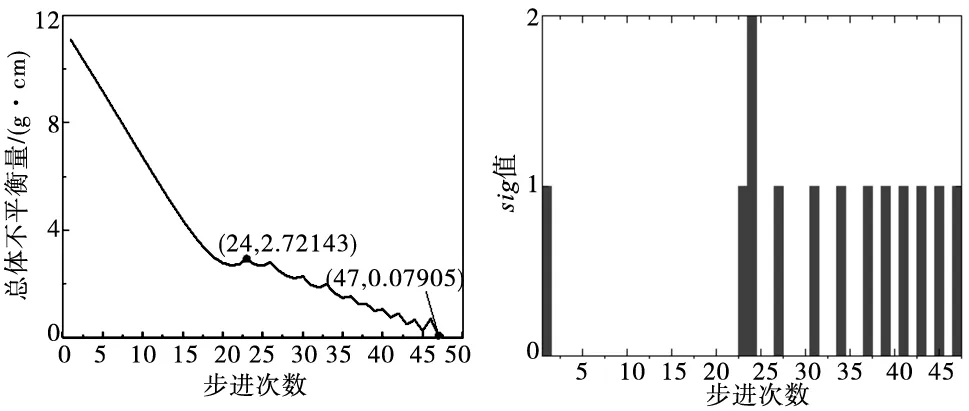
图4 基于贪心算法的双盘异步寻优仿真 图5 寻优过程中状态信号切换

为了更直观的了解双盘异步寻优过程中，两盘异步转动方向以及两盘转动状态切换时间节点，绘制寻优切换信号图，如图5所示，切换信号用sig表示，sig=0表示当前时刻未进行A/B盘切换或转动方向切换；sig=1表示当前时刻进行了A/B盘切换；sig=2表示当前时刻进行了转动方向切换。

从图5中可以得出，在动平衡前期，切换信号sig出现频次很低，说明在该自动平衡阶段前期，对转动盘切换以及转动方向的切换需求很小，节省了切换信号时间以及动平衡系统响应时间，最终表现出对大振动具有快速下降能力。在动平衡中后期，动平衡过程中对A/B盘切换的需求较大，引起了图5中的震荡现象，且越接近完全平衡点，A/B盘切换越频繁。从一定程度上讲，A/B盘频繁切换保证了最终平衡精度，但对平衡速度会有一定的影响。

4 实验验证

为验证基于贪心算法的双盘异步动平衡策略的实际性能，在实验室的转子振动试验台进行了实验，试验台由额定转速1500 r/min的三相异步电动机、BE-1400A型动平衡头以及相应信号采集、处理、控制系统组成，试验台及测控系统如图6和图7所示。

图6 动平衡试验台图7 动平衡测控系统

利用上述的实验装置，对双盘异步寻优策略进行多次实验验证，实验结果汇总如表2所示。

表2 实验结果数据汇总表

振动时域图如图8所示。

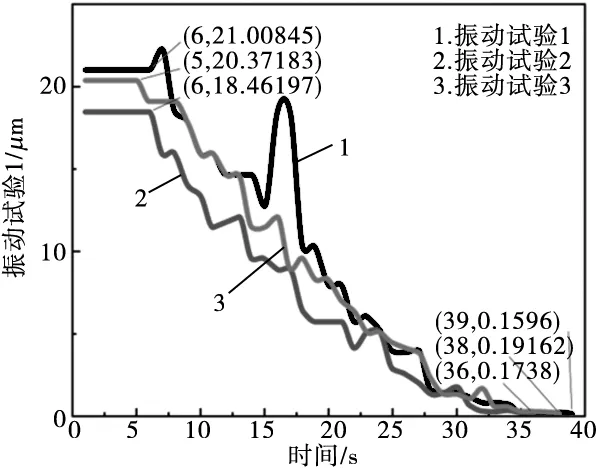
图8 动平衡实验时域图

从表2中可以得出，基于贪心算法的双盘异步动平衡策略，在较恶劣的工况下，可在半分钟左右，将工频振幅从20.37 μm降至0.192 μm，与Schmitt公司的SBS系列动平衡头性能参数对比可以发现，在本自动平衡策略下的动平衡头在平衡时间、平衡精度方面达到了同类前列水平，实现了对转子不平衡故障的快速、高精度自动平衡。

从图8中可以得出，基于贪心算法的双盘异步动平衡策略在平衡过程中，被平衡对象的振幅呈现“振荡下降”的特征，同时在第一次振动实验时域曲线中发现本策略在振动初期概率出现小幅超调现象，振动幅值最终在半分钟左右平均从19.45 μm收敛于0.1～0.2 μm之间，满足精密磨床的精度需要。

5 结论

(1)本文提出的基于贪心算法的双盘异步寻优策略，仅需测定振幅，简化了信号采集装置；算法复杂度小，实时性好；无需动平衡头精确闭环控制相位，也不需要平衡质量的严格同步转动，使得电机驱动式动平衡头可用小型直流电机代替伺服或步进电机，使得该策略适用于结构简单、紧凑的小型直流电机驱动的机械式动平衡头。

(2)实验结果表明，基于贪心算法的双盘异步动平衡策略，在较恶劣的工况下，可在半分钟左右，将工频振幅从20.37 μm降至0.192 μm，并与Schmitt公司的SBS系列动平衡头性能参数对比后，在本自动平衡策略控制下的动平衡头在平衡时间、平衡精度方面均达到了同类前列水平。

综上所述，基于贪心算法的双盘异步寻优策略具有时间复杂度低、平衡时间短、平衡精度高，对动平衡头以及振动采集系统要求低的特点，因此本次策略为研制低成本高精度的砂轮在线自动平衡系统提供了一种实用控制方案。