高频信号注入的永磁同步电机无传感器MTPA控制*

李佩霜，曾成碧，苗 虹

(四川大学电气工程学院，成都 610065)

0 引言

内置式永磁同步电机具有高功率密度、高效率、宽调速范围等优势[1-2]。转子的位置信息的准确获取对于电机的精确控制十分重要，传统的位置传感器增加了系统成本、硬件复杂度和电机尺寸，使系统鲁棒性和可靠性降低。因此，近十年无位置传感器控制技术成为电机控制领域的研究热点[3-4]。

无位置传感器控制可分为两类：适用于中高速的基于模型的无位置传感器控制[5]和适用于零低速的基于高频信号注入的无位置传感器控制[6]。基于模型的方法本质上是基于电机的反电动势，当电机处于零低速状态时，反电动势很小，无法准确检测转子位置信息，只适用于中高速运行。高频信号注入法是实现零低速无位置传感器控制的有效途径，通过向定子电压端注入高频激励，利用电机的凸极性，从电流响应中提取包含位置信息的特定频率分量获取转子位置和转速。李浩源、杜平等[7-9]研究了脉振高频信号注入法和旋转高频信号注入法的无位置传感器控制，二者均不依赖于电机参数，但是信号处理过程复杂，需要大量使用滤波器，系统带宽降低，且注入信号为正弦信号，注入频率低，系统的动态性能受到制约；王莉娜、张国强等[4,10]将高频方波信号注入，提升了注入信号频率，进而提升系统动态性能，但是并没有考虑交叉饱和效应对电机参数的影响所导致的位置估计偏差[11-12]。

通常将id=0控制用于无位置传感器控制技术。然而，为了充分利用IPMSM的磁阻转矩，提升系统效率，有学者致力于将无位置传感器控制和MTPA控制相结合[13-15]。赵文祥等[13]在d轴注入高频脉振电压信号获取转子位置信息，向估计d-q轴电流注入直流信号追踪MTPA工作点，该方法需要注入两种不同的信号，过程较为复杂；ZHANG等[14]基于五相IPMSM的双空间数学模型在三次谐波空间注入实际信号和在基波空间注入虚拟信号，分别实现无位置传感器控制和MTPA控制，但该方法针对多相电机；TANG等[15]用高频虚拟信号注入的方式追踪虚拟q轴电感，同时实现追踪 MTPA轨迹和无位置传感器控制，但是该方法通过反电动势估计转子位置，更适用于中高速范围。

因此，为了实现IPMSM无位置传感器控制下的MTPA控制，本文提出一种零低速范围的高频交替方波信号注入的方法，考虑了IPMSM的交叉饱和效应，建立了高频信号注入下的IPMSM数学模型，在估计坐标系交替注入幅值成一定比例的高频方波信号，通过对高频电流响应提取和处理，获取准确的转子位置信息并实现MTPA控制，并对转子位置估计误差进行补偿，来提升位置估计精度。

1 基于高频方波信号注入的位置估计方法

考虑永磁同步电机的交叉饱和效应，在同步旋转坐标系下的瞬态电压方程表示为：

(1)

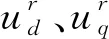
当IPMSM在零低速运行时，可以忽略反电动势和定子电阻电压降，由式(1)知，注入高频信号后的电压方程表示为：

(2)

式中，下标h表示相应的高频信号。为简化分析，认为Ldqh=Lqdh。对于传统的基于高频方波注入的IPMSM无位置传感器控制，将式(3)中高频方波信号注入估计坐标系的de轴。

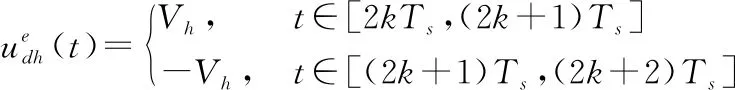
(3)

式中，Ts为正负电压持续时间；Vh为注入电压幅值；k为序列数。由式(2)知，当高频方波信号注入后，得到静止坐标系下高频电流响应为：

(4)

式中，坐标变换矩阵R(x)表示为：

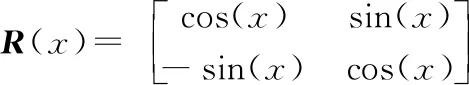
(5)

求解式(4)可得高频电流响应，表示为式(6)：

(6)

式中，θerr为转子位置估计误差，定义为θerr=θr-θe；θr和θe分别为实际的转子位置和估计的转子位置，它们之间的关系如图1所示。

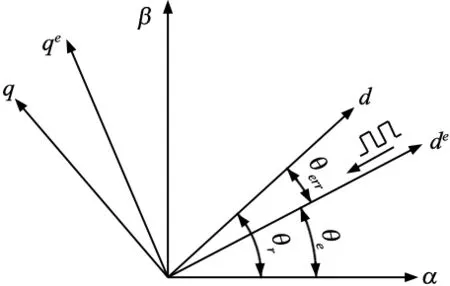
图1 不同参考坐标系之间的关系

静止坐标系中的高频电流响应可通过时间延时器获取，当估计误差θerr趋于0时，具有转子位置信息的高频电流响应的包络可以由式(6)化简为式(7)。

(7)

式中，交叉饱和角θm是由IPMSM的交叉饱和效应产生的相移，与q轴电感和交叉耦合电感有关；Lsh为等效电感。θm和Lsh表示为：

θm=arctan(Lqh/Ldqh)

(8)

(9)

由式(7)可知，其包含转子位置信息和交叉饱和角，如果预先对交叉饱和角进行检测和补偿，通过信号解调并设计合适的位置观测器很容易的得到转子位置信息，这就是考虑交叉饱和效应时，基于估计坐标系直轴注入高频方波信号的IPMSM转子位置估计方法。

2 基于交替高频方波信号注入的无位置传感

器MTPA控制方法

本文采用一种新的高频方波信号注入方法，能同时实现转子位置的准确在线估计和MTPA控制,避免大量的滤波环节，易于实现。首先，提出了所采用的交替高频方波注入序列；然后，解耦位置误差信息并设计转子位置观测器以实现无位置传感器转子位置估计；通过无功功率计算在线调整MTPA工作点；最后，采用查表法[16]对交叉饱和效应引起的位置误差进行补偿。

2.1 交替高频方波注入序列

与传统高频方波注入法仅向估计坐标系de轴注入高频电压信号不同的是，本方法在估计参考坐标系的de、qe轴交替注入幅值成一定比例的高频方波电压信号如式(10)所示，其波形图如图2所示。

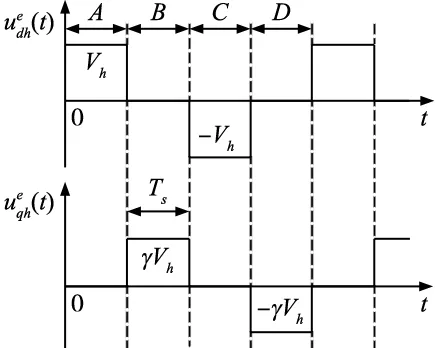
图2 注入序列波形图

(10)

式中，γ为交、直轴注入高频方波电压信号幅值的比值；A、B、C和D为信号注入周期的4个阶段，用区间表示为：

(11)

2.2 位置误差解调及位置观测器设计

由式(7)得到的高频电流响应受到转子位置θr和交叉饱和角θm调制，如果预先检测和补偿交叉饱和角θm，那么采用交替方波注入的静止坐标系下的电流响应推导为式(12)和式(13)，其中，电流纹波中的第二个下标de、qe表示注入高频信号的轴。

(12)

(13)

由于静止参考坐标系的高频电流响应包络中含有位置信息，为避免由反正切函数直接计算转子位置造成的噪音，构造了一个滤波器来平滑位置信号并获取相应的转速。如图3所示，在进行转子位置误差信息解调时采用标幺化处理以消除电感参数影响。在信号注入周期的A、C阶段(即d轴注入)和B、D阶段(即q轴注入)分别连接图3中的实线①和虚线②，进行位置误差解调模式的选择。

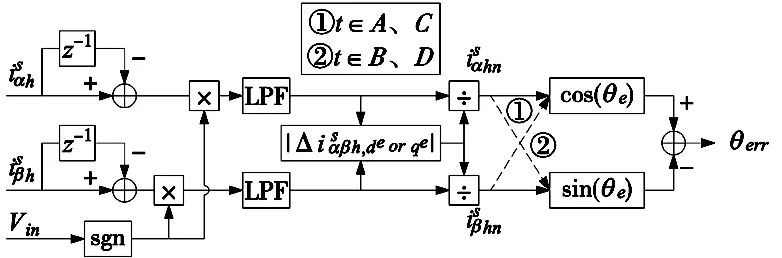
图3 转子位置误差信息解调方法

图4 转子位置跟踪观测器

(14)

式中，f(θerr)为任意正比于θerr的信号，通过合适的调节Ki、Kp和Kd的值，可最终获得转子位置和转速，用于坐标变换和转速控制。

电机运行在零低速时，由于注入时间短，转子位置运动相对较小。位置估计误差选择阶段作为一个离散的采样块，可以由一个零阶保持器建模为：

(15)

2.3 MTPA在线跟踪方法

基于IPMSM的数学模型，通过拉格朗日法可推导出最优电流参考，但需要获取电感和磁通等参数来实现MTPA运行。本文在估计d、q坐标系中利用无功功率的计算将MTPA判别式改写以相应电流纹波的形式表示来消除原有的电机参数影响。在静止坐标系中，可以得到基于式(16)的MTPA决策方法[17]。

(16)

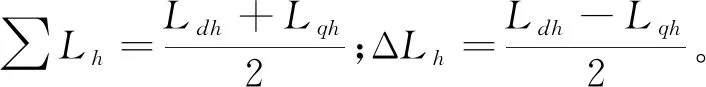
将式(16)的左边通过电流波纹来重新表示为式(17)，而不是通过估计动态电感及磁通来计算，不依赖于任何电机参数。

(17)

对于式(19)的右边，由瞬时功率理论可知，永磁同步电动机瞬时无功功率为：

(18)

将式(17)的右边乘上3/2ωe与式(18)的右边作差，记为ΔQ。如图5所示，通过调整θcomp对转子位置进行MTPA跟踪补偿，控制ΔQ为0，其中，Kc为调节增益。该方法不依赖电机参数，通过在线检测电压电流响应自动调整运行点以追踪MTPA工作点。

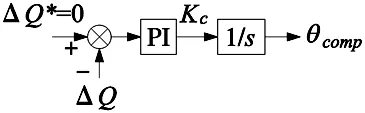
图5 MTPA跟踪补偿

2.4 位置误差补偿

由式(8)，在信号注入周期的A、C阶段和B、D阶段交叉饱和角θm1和θm2可表示为：

(19)

转子位置的相移θm可近似为q轴电流的线性函数[16]。本文通过测量不同负载条件下的θm，进行曲线拟合，可然后利用查表法对交叉饱和引起的位置估计误差进行补偿。图6为稳定运行时，对θm进行补偿前后的转子位置估计结果。可以看出，在没有对进行交叉饱和补偿时，转子估计位置与实际位置误差大约为0.06 rad，而采用补偿方法后的转子位置估计误差约为0 rad，有效提高了位置估计的精度。

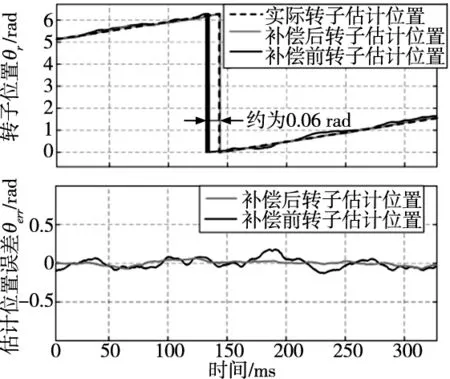
图6 补偿前后的转子位置

3 仿真验证

为验证该控制策略的有效性，在MATLAB/simulink平台上搭建IPMSM的仿真模型，控制结构如图7所示，仿真参数如表1所示。仿真主要验证该控制策略的MTPA工作点跟踪效果、转子位置估计精度。

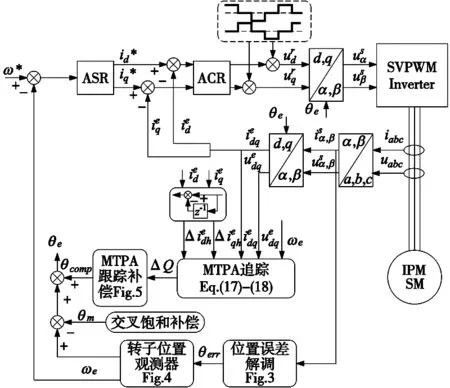
图7 无位置传感器MTPA控制总框图

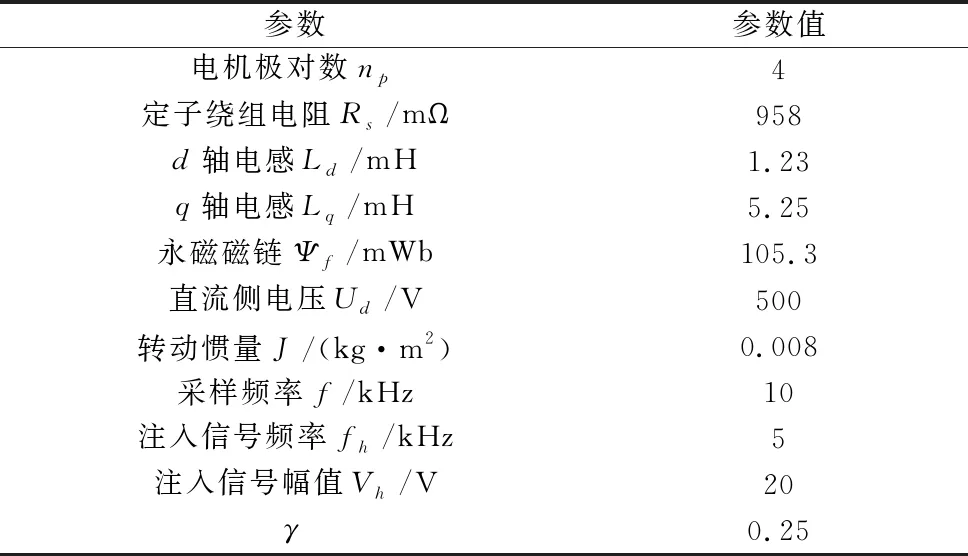
表1 仿真参数

(a) 高频电流响应分量 (b) 高频电流响应分量包络

为验证MTPA算法的有效性，在t=3 s时，将控制算法从id=0控制切换为MTPA控制。其结果如图9a～图9c所示。可以看出从id=0控制切换为MTPA控制后d、q轴电流减小，电流角从1.57 rad增加至1.94 rad，矢量电流幅值从23.41 A减小至21.89 A，在相同转矩下，MTPA控制的矢量电流减小，使得系统损耗降低。

(a) dq轴电流 (b) 电流矢量角

如图10a～图10e所示，当电机在40 r/min的转速下运行时，负载转矩在2 s时从10 N·m增加至20 N·m，再在4 s时降至15 N·m时的A相电流、电机转速和速度误差、交直轴电流和矢量电流幅值、转子位置角和位置估计误差。当给定的负载转矩从10 N·m增至到20 N·m时，d轴电流从-2.1 A降低-5.4 A，q轴电流从9.3 A增加至16.9 A，矢量电流幅值从9.5 A增加至17.8 A；当负载转矩减小至15 N·m时，d轴电流增加至-3.4 A，q轴电流降低至13.4 A，矢量电流幅值减小至13.8 A；稳态时，位置角最大估计误差约为0.04 rad；转矩波动小于4%。因此，当电机的负载给定转矩发生突变时，d、q轴定子电流能快速响应以跟踪MTPA点，使得给定转矩下的定子电流矢量最小，从而提升电机的效率。同时，速度和转子位置跟踪精度不受影响。

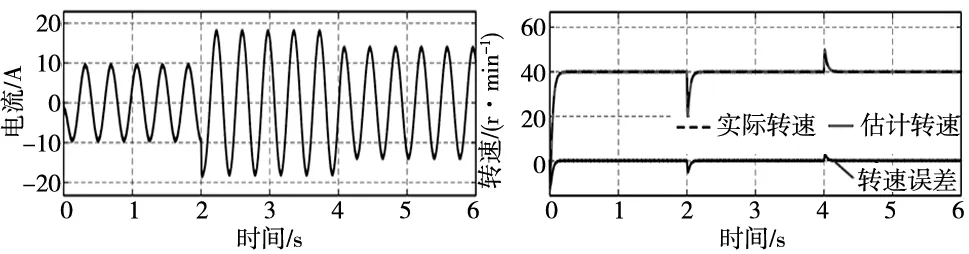
(a) A相电流 (b) 转速估计与误差

如图11a～图11e所示，当转矩指令为12 N·m，速度在2 s时从20 r/min增加至60 r/min，再在4 s时降至40 r/min的仿真结果。可以看出，电机的定子电流在速度突变时经过较小的波动后能快速恢复稳定值。d、q轴定子电流分别稳定在-3.0 A和10.64 A，矢量电流幅值为11.1 A；稳态时，转子位置角最大估计误差约为0.06 rad。因此，当电机的速度发生突变时，表明该系统依然具有较好的动态性能和稳定性。

4 结论

针对内置式永磁同步电机控制系统，提出了一种交替高频方波信号注入的永磁同步电机无位置传感器MTPA控制策略。该方法向估计坐标系的de、qe轴分别注入幅值成一定比例的高频交替方波信号获取准确的转子位置信息，并在线追踪MTPA工作点，此外，还对交叉饱和角引起的位置误差进行了补偿，进一步提升位置估计精度。最后通过仿真验证了该方法具有良好的位置估计效果，动态跟踪性能良好，达到了预期的效果。