基于刚柔耦合动力学的齿轮动态传动误差研究*

2022-11-25王朝兵周神赐邢莹莹

组合机床与自动化加工技术 2022年11期

王朝兵，周神赐，邢莹莹，张龙，洪闯

(1.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室，南昌 330013；2.中车戚墅堰机车有限公司，常州 213011)

0 引言

齿轮传动因其承载能力强、传动平稳、传动效率高等优点，被广泛应用于机械动力传递装置，其力学性能以及动力学特性对装置的传动精度具有重要的影响。石照耀等[1]基于齿轮副整体误差，综合考虑齿轮啮合过程的时变啮合刚度、误差激励等因素，精确地描述了齿轮系统的动力学行为。PALERMO等[2]基于多体齿轮三维模型，探讨了传动误差对齿轮系统振动及噪声的影响。KUBUR等[3]建立多轴齿轮动力学模型，结合试验探讨了传动误差对齿轮系统的激励模态和强迫响应。邓效忠等[4]研究了齿轮在啮合过程中的传动误差，并提出了分析传动误差曲线的时标域方法。洪清泉等[5]基于ADAMS仿真方法并综合考虑齿对啮合相位以及传动轴扭转柔性对多级齿轮传动系统的动态特性进行了研究。卢琦等[6]建立RV减速器刚柔耦合虚拟样机模型，得到制造误差因素对RV减速器传动误差曲线的影响规律。

在齿轮动力学研究中，主要以齿轮传动误差与动态特性之间的关系为研究对象，而对由齿轮系统传动轴的弹性变形引起的齿轮系统动力学特性变化及传动误差方面的研究相对较少，传动轴的弹性变形对齿轮系统传动误差有一定的关系。郑光泽等[7]对变速器传动轴变形对齿轮传递误差的影响分析的研究，分析了传动轴刚度以及齿轮安装位置对齿轮传递误差的影响。本文以直齿圆柱齿轮为研究对象，采用刚柔耦合动力学方法对齿轮传动过程碰撞接触特性进行分析，研究传动轴扭转变形和弯曲变形对齿轮动态传动误差的影响及齿轮轴应力变化规律。

1 直齿圆柱齿轮动力学模型

考虑直齿圆柱齿轮传动轴、支撑轴承的弹性变形及啮合齿面间的摩擦，建立平移-扭转耦合模型[7]。该齿轮传动系统为6自由度的二维平面振动系统，其中4个平面移动自由度，2个转动自由度，如图1所示。

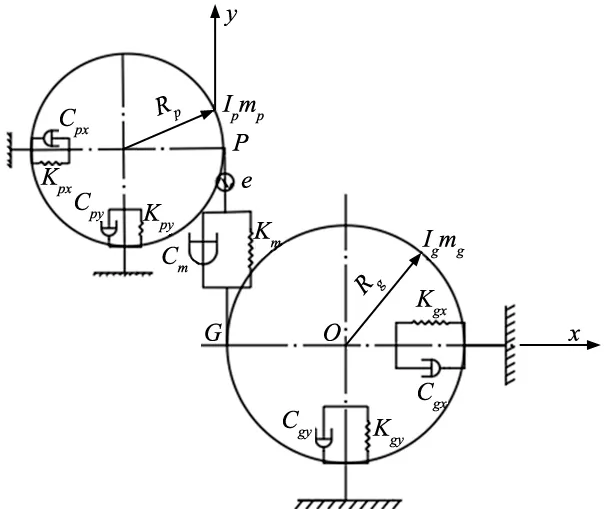
图1 齿轮六自由度模型

其动力学分析模型可表示为：

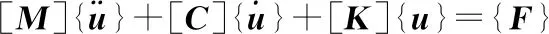
(1)

式中，[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{F}为荷载矩阵；{u}为位移矩阵。

2 齿轮动态传动误差

传动误差是指传动轴单向回转时，传动轴的实际角位移与理论角位移的差值[9]。其表达式为：

(2)

齿轮的传动误差包括因齿轮制造误差、装配误差引起的静态传动误差以及因齿轮和传动轴负载产生扭转变形、弯曲变形导致的动态传动误差。

2.1 传动轴的扭转变形

齿轮啮合传动过程中，传动轴受到转矩T时，会产生扭转弹性变形[10]，其大小为：

(3)

式中，T为轴承转矩；l为轴长；G为材料的剪切模量；Ip为轴的极惯性矩。

Ip可由公式计算得到：

(4)

故齿轮传动系统因传动轴扭转变形产生的动态传动误差为：

(5)

式中，γn为第n对齿轮副的扭转弹性变形；ik为第k-1根轴到第k根轴的传动比。

2.2 传动轴的弯曲变形

在齿轮啮合传动过程中，传动轴在法向力Fn作用下，沿啮合线方向发生弯曲弹性变形，如图2所示。

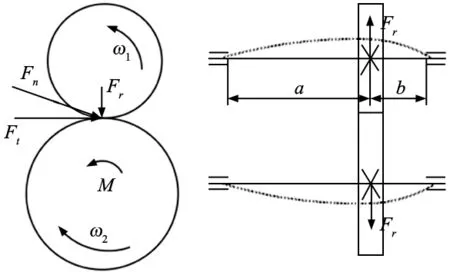
图2 传动轴弯曲变形示意图

传动轴在齿轮位置沿啮合线方向的弹性变形量[11-12]为：

(6)

式中，Fn为法向啮合力；a、b为齿轮到两轴承端的距离；E为弹性模量；dz为轴直径。

传动轴由弯曲变形导致齿轮传动副的动态传动误差为：

(7)

式中，f为传动轴沿着齿轮传动的啮合线方向发生弯曲变形量；a为压力角。

齿轮传动系统因传动轴弯曲变形产生的动态传动误差为：

(8)

传动轴由于弹性变形引起系统的动态传动误差ζ为：

ζ=∑γ+∑χ

(9)

2.3 齿轮传动计算实例

实例直齿圆柱齿轮参数如表1所示。

表1 齿轮参数

直齿轮圆柱齿轮材料模型参数如表2所示。

表2 材料参数

结合从动轮的传动轴模型参数如图3所示，由式(3)～式(5)计算得传动轴传动误差为：γ=1.79′。

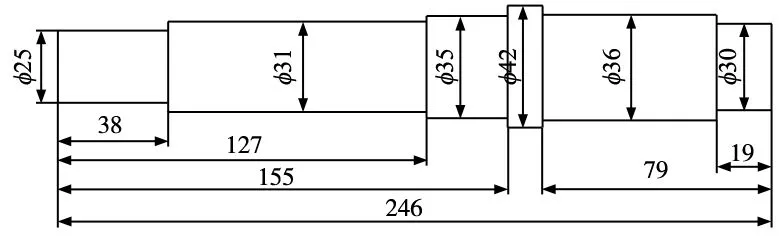
图3 传动轴模型参数

对传动轴进行受力分析如图4所示。

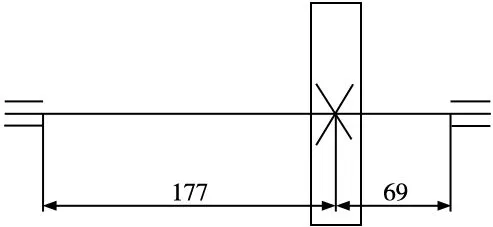
图4 传动轴受力分析

结合图4传动轴受力分析，由式(6)～式(8)计算得到由啮合力导致传动轴弯曲变形引起的传动误差为：χ=0.555′。由式(9)计算可知传动轴由扭转变形和弯曲弹性变形引起的理论计算传动误差值为2.345′。

3 齿轮系统动力学仿真分析

3.1 基于Adams的接触碰撞算法

应用Impact函数计算两齿轮间的接触力，该接触力由两构件相互切入产生的弹性力和相对速度产生的阻尼力两部分组成。其函数表达式为[13]：

(10)

式中，K为接触刚度系数；e为接触指数；q为接触距离；q0为接触函数的距离变量；C为最大接触阻尼；d为达到最大阻力时两物体的穿透深度。

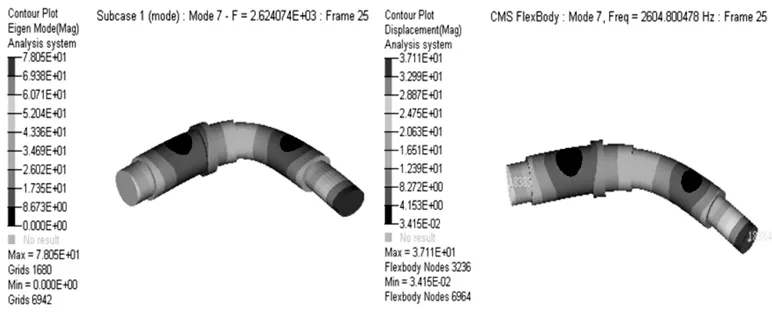
当q≥q0时，不发生接触，接触力为0；当q

刚度系数K取决于接触物体的材料和结构形状，其表达式为：

(11)

对于啮合直齿轮，接触点处的当量半径分别为：

(12)

式中，d′为节圆直径；α′为节圆压力角。

结合齿轮模型参数表1，由式(11)、式(12)计算齿轮刚度系数K=8.61×105N/mm3/2，接触指数取值1.5；阻尼系数取值30 N·s/mm；最大击穿深度取值0.1 mm；接触体之间的摩擦力采用库仑摩擦，动摩擦系数取值0.05；静摩擦系数取值0.08。

将实例传动轴导入到HYPERMESH中进行离散化处理，生成实例传动轴的模态中性MNF文件。并对实例传动轴进行自由模态仿真，通过对比柔性体模态与实例传动轴的自由模态的频率值与变形趋势对生成的MNF文件进行验证。以第7阶模态频率与模态振型为例，结果如图5所示。

(a) 模态振型 (b) 模态频率

由图可知，传动轴的第7阶自由模态频率为2 624.074 Hz，柔性体模态结果文件第7阶模态频率为2 604.80 Hz，其频率误差为0.73%，且模态振型一致，说明利用HYPERMESH生成的模态中性文件是正确的。

3.2 刚柔耦合动力学仿真及分析

将齿轮系统三维模型导入多刚体动力学软件ADAMS中，并将柔性化的传动轴代替刚性传动轴。在输入端应用阶跃函数STEP，使输入轴转速在0.1 s内由0增加到4800 °/s，输出端施加16 500 N·mm的负载。仿真时间设置为1 s，进行仿真，截取0.1 s～0.4 s的仿真结果进行统计分析，结果如图6所示。