曲线梁桥减震榫结构设计及减震性能分析*

李 迪，朱伟庆

(1.上海海事大学 海洋科学与工程学院，上海 201306；2.长安大学 公路学院，陕西 西安 710064)

0 引言

随着我国交通建设领域的快速发展，桥梁作为重要的交通基础，其运输量的增加对桥梁提出了更高要求.建设施工中，必须保证桥梁结构有优越的抗震性能，才能保障交通运输的安全运行.科学分析桥梁结构的极限承载力和抗震性能，对于保证桥梁的使用能力显得十分重要.要通过不断的研究，对桥梁的极限承载力和减震抗震性能建立起更加科学更加全面的评估方式[1-3].桥梁的极限承载力是指桥梁完全崩溃前所能承受外荷载的最大能力，其大小与以下因素有关：材料特性，如极限强度、应力应变关系等；结构和构件的刚度及几何尺寸，如面积、惯矩等；结构所处的状态，如施工阶段、运营阶段等；结构承受的荷载形式，如恒载、组合荷载等；荷载的加载路径.不同施工方法、不同荷载形式和加载路径，桥梁结构极限承载力不同，即极限承载力不是一个定值[4].为了提高曲线梁桥的抗震能力，近年来开发了一个新型的减隔震装置，即减震榫.减震榫的工作状态为塑性耗能状态，在地震作用下往复运动直至发生低周疲劳破坏，低周疲劳寿命是减震榫非常重要的工作性能参数.减震榫设置在主梁与桥墩连接处，因其具有较大的延性耗能能力，能够耗散大部分地震能量，可以从根本上减少桥身自身振动、增加抗震强度及增加桥梁平面的阻尼作用等等，在一定程度上可以减少地震带来的后续反应，可以有效地保护桥墩和上部梁体结构的安全[5-7].该减震系统已成功应用于多条高铁线路的建设工程当中，实践证明其具有良好的应用价值.

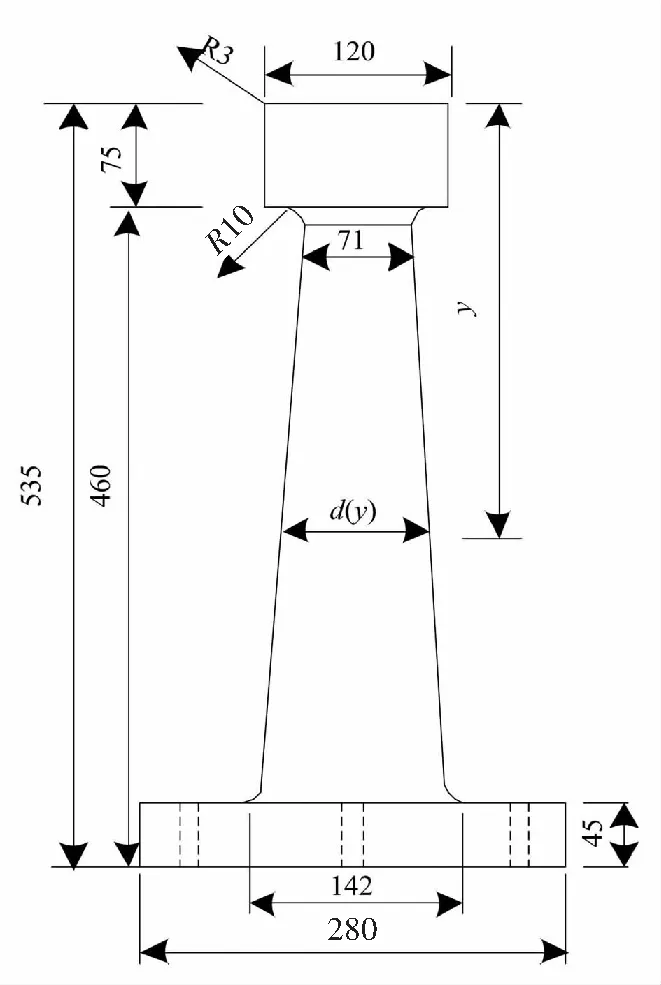
图1 减震榫结构Fig.1 Damping tenon structure

1 曲线梁桥减震榫结构设计

1.1 减震榫设计原理

减震榫结构设计是以曲线桥梁减震力学理论为基础的，利用双曲面设计原理来减少桥身晃动.本文提出了将曲面支座系统与减震设计相结合，提高了桥身的隔震能力，使桥梁能够支持高速列车的持续快速通过.减震榫结构如图1所示.

减震榫杆是一个规则的圆柱，为了减小减震榫杆的摩擦力，要求圆柱表面必须是光滑的.为了促使桥墩底部与桥墩之间更加牢固结实，固设计成方形形状，且用螺栓衔接[8-10].

桥梁减隔震技术的主要实现方式是在梁体和墩台的连接处安装可以减隔震的支座.支座有很多种，比如盆式的橡胶支座、铅芯橡胶支座、板式橡胶支座.这些橡胶支座通过阻断连接的方式层层阻击，将地震能量尽可能减到最小.有证据表明，铅芯橡胶支座在降低桥梁振动上有非常显著的效果.但是受到橡胶质地的限制，橡胶支座往往比较脆弱，无法适应铁路行驶带来的振动.并且在地震发生后，余震的压力最后才会到达桥墩，减少了对支座系统的伤害，虽然阻尼榫头会变形，但仍旧会起到一定的减震作用[11].

为了更好地实现减震榫的塑性分担作用，控制减震榫变化的合理范围，对其干扰参数进行取值计算，在计算过程中，忽略榫头的影响，横截面直径变化可以表示为：

d(y)=ay1/3，

(1)

式中：y代表传力段顶端至横截面的距离；a代表截面常数值[12].

基于平衡力学理论[13]，可以将减震榫的弹性范围表示为：

(2)

式中：fy代表钢材的屈服强度[14]；L1表示截面的整体高度.

公式(2)除了可以利用参数来改变其基础性能不受任何因素影响，因此要调整其结构就要将参数控制在一定的范围.

1.2 减震榫刚度计算

减震榫对刚度有一定要求.梁体与桥墩通过减震榫相连，在强烈震动时桥墩的刚度会发生变化，所以减震榫同时要面临两方面要求，一是要具备足够的刚度以应对平常使用，二是要有较好的延伸性，以便在地震发生时能够大幅吸收能量.选取三条天然地震波对隔震桥梁进行非线性时程分析.地震波沿桥梁纵向输入，采用 IDA 的计算方法，加速度峰值在 0.2 g～0.6 g 中变化，增幅为 0.1 g，统计时程分析结果并分析[15].桥梁的减震结构与桥墩的高度有关，桥墩的重力与减震榫同时工作就会发生对抗，大大减小减震榫的稳定性，为此对其刚度进行计算，两个作用力同时运行时的组合刚度为：

K=KdKs/(Kd+Ks)，

(3)

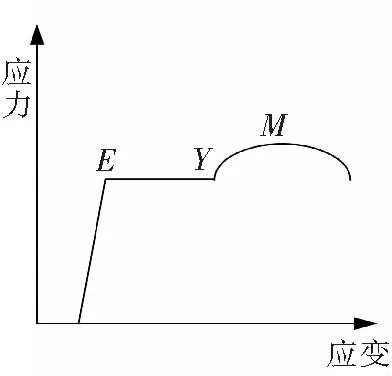
图2 单轴拉伸应力应变曲线Fig.2 Uniaxial tensile stress-strain curve

式中：K代表组合后的桥墩线刚度；Kd代表原桥墩线刚度；Ks代表减震榫线刚度[16].

表1 减震榫的力学参数

在此基础上，将拉伸应力应变曲线表示如图2.

1.3 减震榫结构设计

按照工程的要求模拟减震榫的工作原理，以地震区的桥梁为研究对象，依据地区特点与周围环境设计地震减震榫，其内部结构为减震杆、底座受力装置以及墩台锚固定装置构成[17-20].

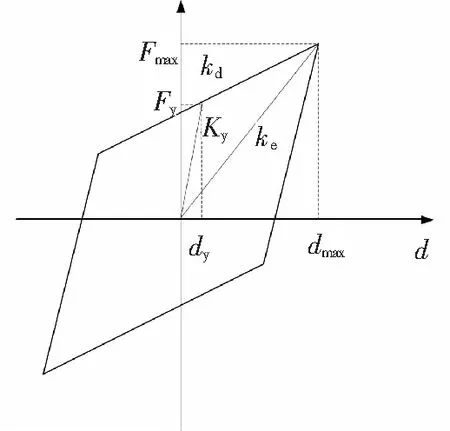
图3 减震榫力学模型Fig.3 Mechanical model of shock-absorbing tenon

传力套筒是一个组合结构，它包括上下两个分支结构，上部结构中心内部是以球形腔体为核心工作原理，其整个结构内部没有阻隔，减震块一般存在于套筒下部，与外部仪器连接时把减震榫固定在套筒上部，与球形腔体相连成为一个整体，按照曲面桥梁的结构设计要求，将套筒内的腔体与减震榫之间的距离设置为20 mm。单个减震榫的力学参数设置如表1.

同时，在经过20 mm的无效位移后，直接连接减震榫的顶部，促使减震榫只能进行水平方向的移动，以减少能量损耗.

2 减震榫力学模型构建

减震榫力学模型如图3所示.

图3中，Fy代表材料屈服力，Ky代表初始刚度，dy代表屈服位移，Fmax代表最大承载力，dmax代表最大位移参数，kd代表屈服后刚度参数，ke代表等效刚度.

等效刚度直接决定最大刚度与桥身曲线的斜率，将其表示为：

(4)

在此基础上对减震榫的等效阻尼比进行计算，假设减震榫和黏性阻尼器在一个周期内消耗能量相同，那么对黏性阻尼器中滑块的往复运动产生的正弦函数计算为：

x(t)=Asinωt，

(5)

式中：A代表滑块的位移参数；ω代表滑块振动频率，进一步将力学模型表示为：

(6)

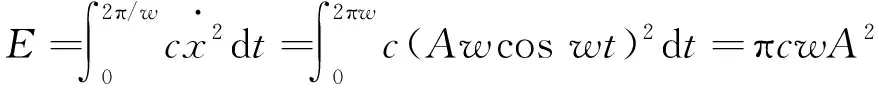
式中：c代表阻尼器的阻尼系数；k代表阻尼器刚度值；m代表质量参数；E代表阻尼器在一个周期内消耗的能量值.

基于上述过程建立起减震榫力学模型，为结构设计提供参考.

3 地震力简化计算方法

在对减震榫地震水平简化分析时，采用基于单墩力学模型反应谱方法计算，计算步骤如下所示：

第一，假定减震榫的位移值为Δ(mm)；

第二，对墩顶位移对应的水平合力计算：

P0=m·Fj+μ·M，

(7)

式中：M代表阻尼比；μ代表梁部重力；Fj代表支座摩擦系数.

第三，计算等效刚度和桥墩的合成刚度，将计算公式表示为：

(8)

式中，P0代表桥墩水平线刚度.

第四，计算减震榫装置与桥墩合成阻尼，将计算公式表示为：

(9)

式中，ξp代表桥墩的阻尼系数.

第五，计算墩顶地震水平力与假定位移对应的水平合力，如果墩顶地震水平力与水平合力之间相对误差小于1.0 %，则所得到的结果为结构在地震作用下的响应值，并重复上述步骤直到获得符合要求的结果为止，将计算公式表示为：

F=α·β·η·M，

(10)

式中，α代表地震峰值加速度参数.

通过上述计算对地震力简化计算，为实际计算提供基础.

4 减震性能分析

4.1 分析模型

由于实际工程中的减震榫结构较大，为此在减震性能分析上采用ANSYS有限元程序建立全桥空间分析模型.全桥空间分析模型如图4所示.

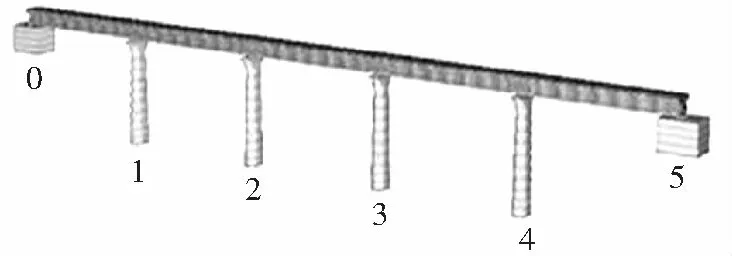
图4 全桥空间分析模型Fig.4 Spatial analysis model of the whole bridge

在分析时主要考虑两种情况：

工况1，桥身、桥墩与底座之间要满足混合式支座连接；

工况2，桥梁、桥墩与底座三者之间要固定成一个整体，并且依靠减震榫与底部系统相互作用.

基于桥梁的自身结构，最佳单元格格式为Beam188单元，利用其稳定与弹性性能来模拟梁体和桥墩，按照曲面支座的适用原则，建立弹簧单元模拟制作，而减震榫的相似结构就用Combin40非弹性单元来代替，明确减震榫结构的位移方向为加速度方向，使桥梁与桥体之间只存在较小振动，不影响实验进行.当桥墩处于塑性状态时会存在最大弹性压力，产生的能量达到峰值，地震会对桥身产生伤害，而更大的压力通常在桥体震动的返回阶段，因此上述两种工况可以满足桥墩受力分析的要求.

4.2 减震性能分析

为了增加桥梁的稳定性，使用滑动支座系统代替桥梁底座结构以稳定桥梁自身结构，有利于高速列车的安全行驶.经过多次实践检验证明，只有在满足桥身自身运转周期为0.222 s和0.400 s的时候，才能尽可能地接近理想状态.同时，为了检验减震榫的性能，分别设定三个不同的周围环境来进行对比分析，得到其地震波参数如表2所示：

表2 输入地震波列表

表2中，可以得出地震波最大时，其加速度也会随之上升，将严重影响减震榫的抗震性能，为了减小或者忽略减震榫的干扰因素，着重表现地震时桥梁的抗震能力，应该将每个波的峰值全部设置成400 cm/s2.

表3为两种工况的地震响应峰值：

表3 Taft地震波作用下地震响应峰值

基于上表可知，将工况2与工况1对比可知，工况2下的两个桥墩底部的重力、桥墩外形的弧度以及墩顶的位移峰值均在同时变小，表明其减震效果超出预计，较工况1应用效果好.

4.3 减震榫三级性能指标

分析提出的减震榫-滑动支座系统在3级地震水平下的反应，将地震波的大设置成3个不同的值分别模拟支座系统的位移值，分析其减震性能，这三个值分别为0.1 g、0.3 g、以及0.6 g模拟小震、中震和大震，结果如表4所示：

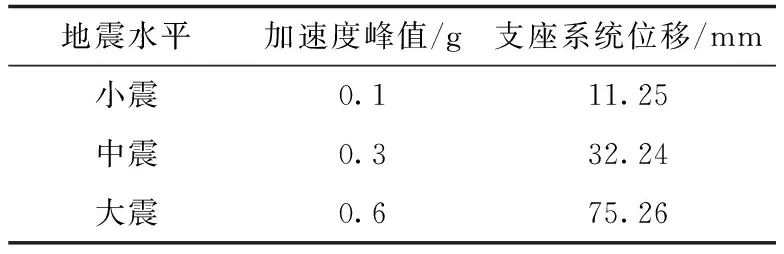
表4 减震榫三级性能分析

基于上表可知，在处于小震状态时减震榫出现屈服现象，但是变形较小，位移也较小，因此直接使用即可；在处于中震状态时，减震榫发生的变形较大，达到地震峰值时，减震榫位移最大，但是仍小于表1中的极限位移，说明所设计的减震榫结构性能较强.

4.4 不同墩高对桥梁减震效果的影响

依据实际工程情况，选取5种墩体，墩高分别为4 m、8 m、12 m、16 m、18 m，在分析过程中，保证其他参数不变，各个桥墩参数如表5所示.

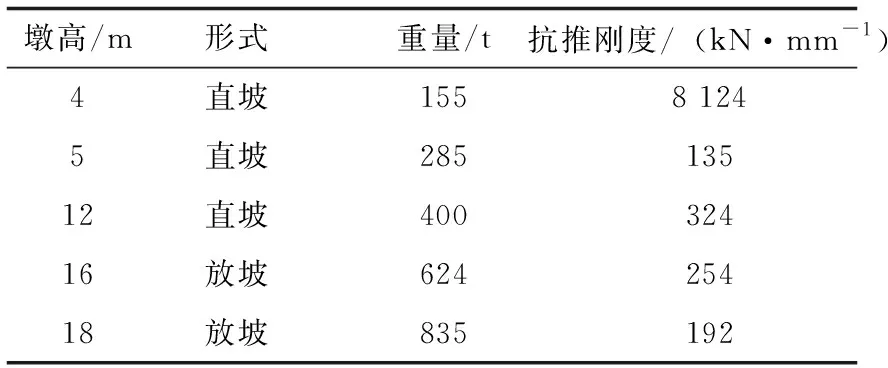
表5 桥墩参数

图5为各个桥墩的减震率变化曲线.

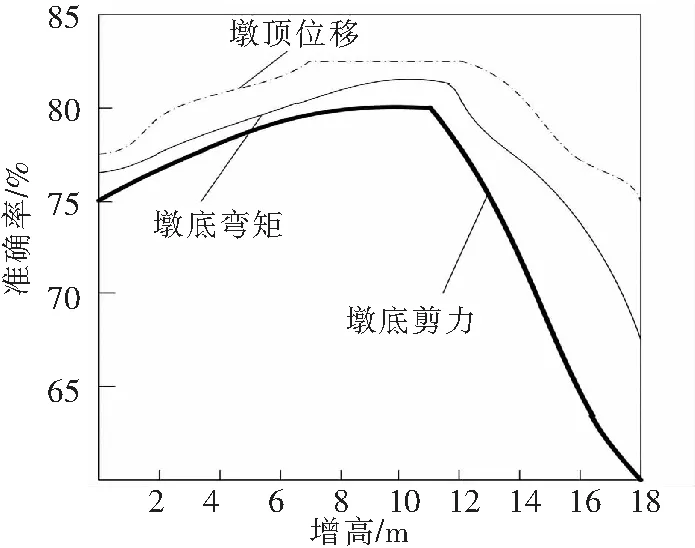
图5 不同墩高的减震率变化曲线Fig.5 Variation curve of shock absorption rate of different pier heights

基于图5可知，墩高与减震效果密切相关，在墩高小于12 m时，减震率随着墩高的增加呈上升趋势，在墩高达到最高时，其减震率能够达到85 %以上，但是随着墩高继续增加后，其减震效果则出现迅速减弱的情况.发生这种情况的原因是墩高自振周期较短，梁体位移量较小，减震榫不能进入塑性阶段，而当墩高继续增加后，减震榫对其动力特性影响变小，因为桥梁本身自振周期较长，从而导致减震效果降低.

5 结束语

基于上述过程完成曲线梁桥减震榫结构设计，并对减震性能进行了分析，得到以下结论：

(1)研究的减震榫基于底座的稳定性与桥墩的底座相互依靠，形成一个循环的支座系统，其承担的压力主要作用在减震榫上，竖直方向的压力主要由桥墩底座来承担，使两个压力具有不同方向，既减少了桥体损伤，还能够大大延长桥梁的自振周期，提高了减震效果；

(2)通过试验分析发现，增高对减震榫结构的减震效果有较大的影响，在实际工程中需要在保证其使用功能的前提下，对不同桥梁结构的减震榫参数进行设置.

此次研究虽然获得了较好的应用效果，但是在不同的工程设计中还是需要结合实际情况做具体设计，进一步提高曲线梁桥的减震效果.