双弧形桥塔斜拉桥静力与稳定性分析

张成毅，何茂维

（1.成都市简州新城投资集团有限公司，四川 成都 641400；2.中国市政工程西南设计研究总院有限公司，四川 成都 610081）

0 引 言

随着我国桥梁建设事业的大力推进，跨海大桥的设计[1]也得到迅猛发展。跨海大桥由于使用环境恶劣，常常需要选定特殊的桥型，并对桥梁进行多种荷载工况下的受力计算，以此确保跨海桥梁的安全性。斜拉桥拉索[2-3]对主梁提供了竖向弹性支撑和轴向压力，使得其在跨海大桥中应用较多。但斜拉索的垂度效应常常使得斜拉桥几何非线性[4]较为明显，而跨海大桥风环境复杂，会加剧结构非线性受力情况，因此对斜拉桥的抗风稳定性[5-7]、静力稳定性[8-9]研究较多，但对异性双弧形桥塔的跨海斜拉桥抗风稳定性研究相对较少。

基于上述研究，以某双弧形桥塔的跨海斜拉桥为研究对象，探究在成桥状态下可能出现的各种荷载作用对静力稳定性的影响问题。

1 工程概况

1.1 桥梁概况

以某跨海大桥为研究背景，该桥型为双塔双索面预应力混凝土梁斜拉桥，跨径布置为（150+328+150）m。为减塔身弯矩，尤其是塔梁连接处和塔脚处的弯矩，以及减小温度对结构内力的影响，主桥采用三跨连续塔梁固结体系，塔高125 m。全桥共288根斜拉索，共11 种拉索规格。主梁采用PK 断面预应力混凝土主梁，梁高3.2 m。索塔处梁段水平底板板厚90 cm，斜底板厚为38 cm，中腹板厚50 cm。边跨现浇段顶板厚40 cm，底板加厚至100 cm，斜腹板厚100 cm，中腹板厚100 cm。两者均由标准断面线性过渡。

桥塔采用C50 混凝土，主梁采用C55 混凝土，桥墩、承台等采用C40 混凝土，拉索采用抗拉强度为1 770 MPa 的平行钢丝。

1.2 风参数

营运阶段：重现期100 a，基本风速为36.2 m/s，设计基准风速为42.4 m/s。

风速随高度变化模式（Ud=U10（Z/Z10）α）中的桥位场地幂指数α=0.12。

2 模型及自振特性

2.1 有限元模型

根据该跨海大桥的实际情况，基于Midas/Civil 2019 建立其有限元模型。由于结构跨度大、拉索结构多，且桥塔结构形状较为特殊，导致其结构非线性较为明显，故对拉索的垂度效应用Ernst 弹模修正公式进行考虑，用仅受拉的桁架单元模拟斜拉索，其余结构如主梁、桥塔、桥墩等均采用梁单元模拟。主梁在桥墩处向上放开，塔梁采用弹性连接进行约束，塔底、墩底均固结，其有限元模型如图1 所示。

图1 有限元模型

2.2 自振特性

根据前述分析可知，该桥几何非线性较为明显，为便于后续静力与稳定性的计算，有必要对结构自振特性进行分析。结构自振特性分析方法主要有子空间迭代法、多重Ritz 向量法、分块兰索法等，对于几何非线性问题，采用子空间迭代法较为良好。基于子空间迭代法求得的前5 阶结构自振频率及振型描述见表1，前2 阶自振振型如图2 所示。

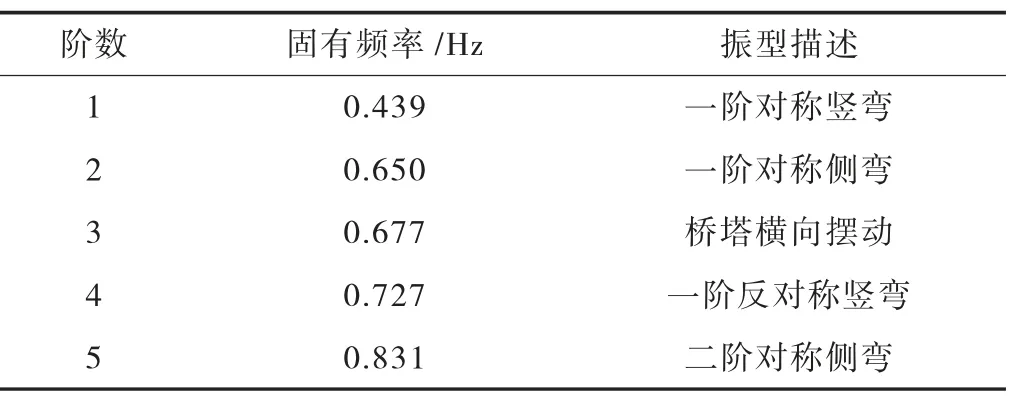
表1 结构自振特性

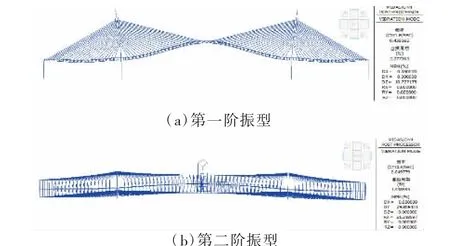
图2 前2 阶自振振型

分析表1 可知，该桥前5 阶主要振型为竖弯和侧弯，说明在横风以及竖向地震运动下可能会产生较大的位移，影响行车舒适度和结构安全。

3 荷载工况

该桥营运阶段主要的荷载包括结构自重、二期长期效应组合、拉索张拉力、主梁结构预应力、结构配重以及横向风荷载。除横向风荷载外，其余荷载在施工完成成桥阶段均已产生，二期长期效应组合根据桥面铺装、护栏等附属设施重量计算，其值为15.76 kN/m，而拉索及预应力根据实际情况设置，混凝土结构容重取26 kN/m3。

为了更为详细地给出各种荷载值，有必要按照规范计算出作用在桥塔和主梁上的风荷载值，便于加载至模型中。

结构静力风荷载按《公路桥梁抗风规范》（JTG/T 3360-01—2018）取值，限于篇幅，此处仅给出主梁高度处的静风荷载计算。

该桥营运阶段基本设计风速为36.2 m/s，设计基准风速为42.4 m/s，风速随高度变化模式见式（1）。

式中：α 为桥位处的场地幂指数，α = 0.12。

该桥水平加载长度为628 m，等效静阵风系数根据抗风规范，依据水平加载长度进行查表取值，其值为1.2015，故等效静阵风风速为50.94 m/s。

横风作用下主梁单位长度上的等效静阵风荷载按式（2）计算。

式中：ρ 为空气密度，取1.25 kg/m3；Ug为等效静阵风风速；CH为主梁横向力系数，根据主梁的高度和宽度进行计算，其值为1.3；D 为主梁投影高度，取3.2 m。

根据式（2）可计算得到主梁单位长度上的等效静阵风荷载为6.75 kN/m，而根据抗风规范可计算得到桥塔单位长度上的等效静阵风荷载为3.15 kN/m。

4 静力与稳定性

4.1 静力计算

（1）主梁内力

在长期效应组合作用下主梁弯矩和剪力分别如图3 和图4 所示。

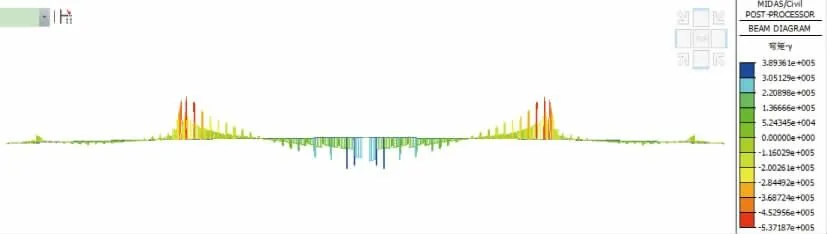
图3 主梁弯矩（单位：kN·m）

图4 主梁剪力（单位：kN）

分析图3 和图4 可知，在长期效应组合作用下塔梁结合处的弯矩和剪力最大。这是因为该桥为塔梁固结体系，整个主梁相当于一个三跨悬臂梁，在塔梁连接处负弯矩较大，在跨中处正弯矩较大，故在塔梁结合处主梁上翼缘应布设一定数量的预应力钢筋。此外，由于塔梁结合处的剪力较大，也应在塔梁结合处设置一定数量的弯起钢筋，以减小主梁斜截面开裂。

（2）桥塔内力

桥塔弯矩和剪力分布如图5 和图6 所示，便于论述，桥塔各截面如图7 所示。

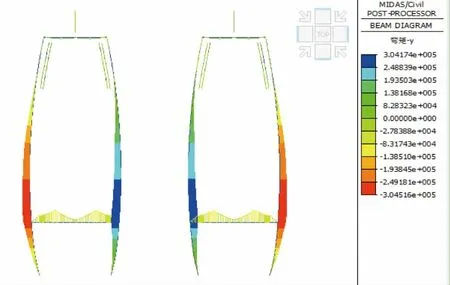
图5 桥塔弯矩（单位：kN·m）

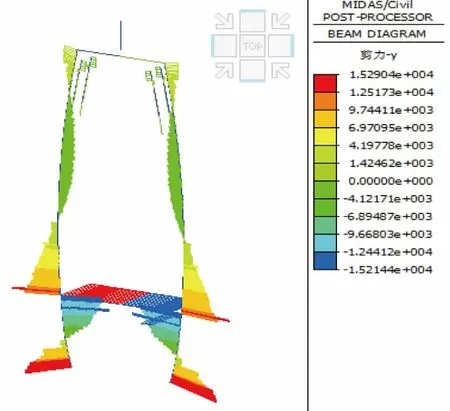
图6 桥塔剪力（单位：kN）

图7 桥塔各截面示意图

分析图5 和图6 可知：

a. 长期效应组合作用下桥塔弯矩并不是发生在塔底，而是发生在下横梁交接处，最大值为3.05E+05 kN·m，这是因为该桥塔为弧形异形桥塔，受力较为异常；

b. 长期效应组合作用下桥塔多个截面剪力较大，主要发生在塔底、下横梁以及下横梁交接处，最大值为1.53E+04 kN。

（3）拉索内力

长期效应组合作用下各拉索轴力等值线如图8所示。分析图8 可知，拉索最大轴力也并非发生在跨中最长拉索处，而是发生在跨中倒数第七长拉索处，这与常规斜拉索受力略有异同。

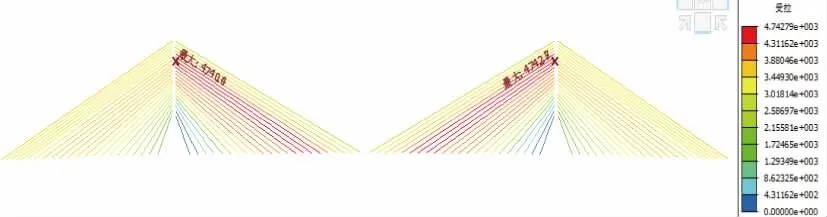
图8 长期效应组合作用下拉索轴力（单位：kN）

（4）位移

在准永久组合和频遇组合下各关键控制点位移见表2。

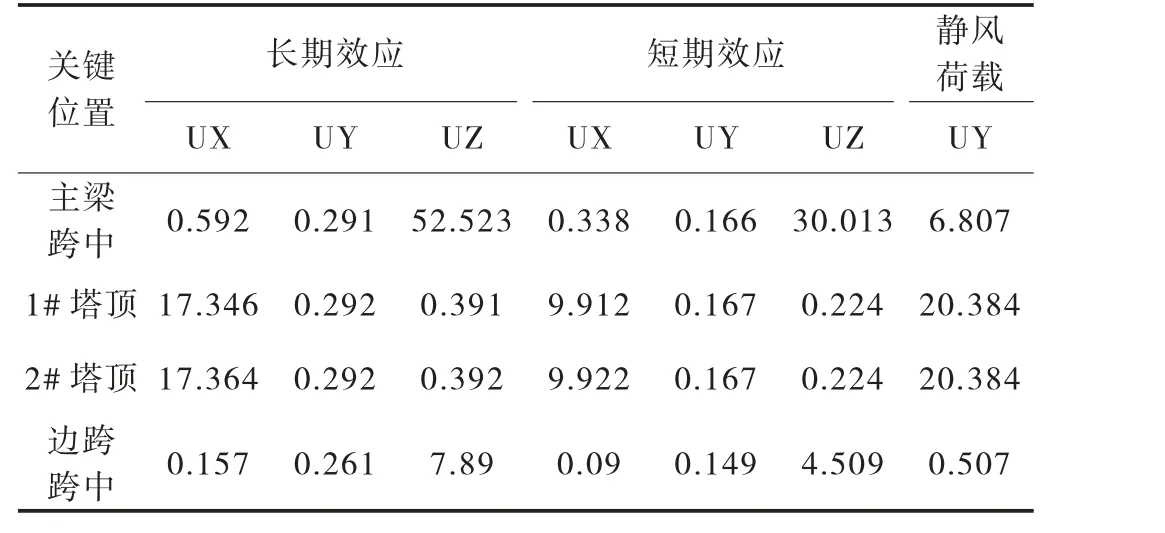
表2 关键控制点位移 单位：mm

分析表2 可知：

a. 长期效应下各关键控制点位移略大于短期效应下各位移值；

b. 长期效应下主梁跨中竖向位移和塔顶纵向位移最大值分别为52.523 mm 和17.364 mm，而桥塔纵横向位移不到1 mm，说明长期效应作用下主梁跨中竖向位移更值得关注；

c. 横向静风荷载下主梁跨中横向位移约为6.807 mm，而塔顶横向位移约为20.384 mm，与整个塔高相比也较小，基本上无明显影响。

4.2 稳定性

在营运阶段6 种荷载共同作用下的前2 阶稳定屈曲模态分别如图9 和图10 所示。

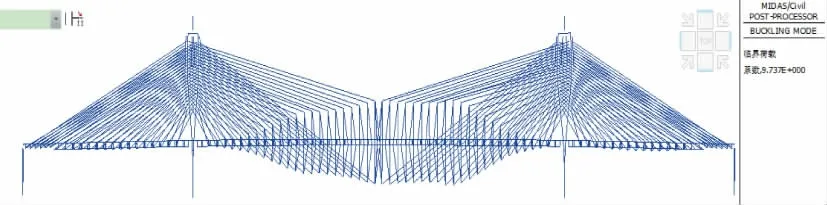
图9 一阶屈曲模态（稳定系数：9.74）

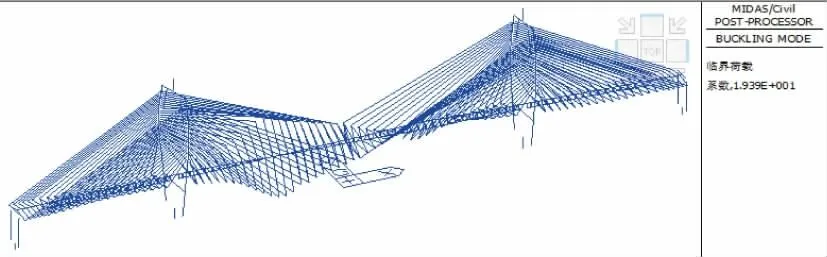
图10 二阶屈曲模态（稳定系数：19.39）

分析图9 和图10 可知，前2 阶稳定屈曲模态系数均大于4，也即在营运阶段不会发生整体失稳。

由于斜拉索为受拉结构，而主梁为受压结构，因此结构的几何非线性，比如斜拉索垂度效应、制造缺陷、施工与设计偏差等，使得斜拉桥为偏心拉压结构；也即由于几何非线性的影响，存在初始弯矩的作用，进而降低了斜拉桥线弹性范围，增加了弹塑性的范围，使得斜拉桥也更容易发生结构失稳。因此，在设计和受力分析时，要考虑结构几何非线性的影响。

5 结 语

（1）在长期效应组合作用下塔梁连接处负弯矩较大，在跨中处正弯矩较大，故在塔梁结合处主梁上翼缘应布设一定数量的预应力钢筋。此外，由于塔梁结合处的剪力较大，也应在塔梁结合处设置一定数量的弯起钢筋，以减小主梁斜截面开裂。

（2）长期效应组合作用下桥塔弯矩并不是发生在塔底，而是发生在下横梁交接处，最大值为3.05E+05 kN·m，且桥塔多个截面剪力较大，最大值为1.53E+04 kN。

（3）长期效应下主梁跨中竖向位移最大约为52.523 mm，而塔顶纵向位移为17.364 mm；横向静风荷载下主梁跨中横向位移和塔顶横向位移分别为6.807 mm 和20.384 mm。

（4）在营运阶段6 种荷载共同作用下前两阶稳定屈曲模态系数均大于4，即在营运阶段不会发生整体失稳。