基于动网格的涡轮流场仿真方法及特性分析
2022-11-23徐学文
徐学文,曲 凯,白 玉,2
(1.海军航空大学,山东烟台 264001;2. 61035部队,北京 102205)
涡轮是直接带动涡轮喷气发动机压气机旋转对空气做功的重要部件。近年来,随着无人机、导弹等装备快速发展,涡轮喷气发动机的应用越来越广泛,因此,对涡轮特性的研究也越来越多[1]。当前,对涡轮流场特性分析主要基于实验的方法和气体动力学分析[2-4],但是,实验成本高昂,相似条件较难满足,实验结果可参考性不大[5-6],而气体动力学分析也只能做简单的量化计算和定性分析[7-10]。随着计算机仿真技术发展,通过流场仿真计算来研究涡轮流场特性的越来越多,由于建模和计算的复杂性,以及三维仿真成本高昂[11-12],故大多采用一维、二维流场稳态仿真计算[1,13-14],从而提高涡轮流场特性分析效率。本文基于动网格的二维流场仿真技术,探讨涡轮旋转条件下的流场仿真方法,计算涡轮流场参数变化,开展涡轮流场特性分析。
1 仿真计算模型
1.1 流场模型
本文选择单级轴向涡轮作为研究对象,它由一级导向器(静子)和一级涡轮(转子)组成,从外界进来的高压气体首先经过导向器高速膨胀,在出口处获得足够速度后,直接冲击在涡轮叶片上,推动涡轮旋转做功,最后从涡轮出口高速喷出。
气体在导向器和涡轮叶栅通道流动过程中,速度、压力与温度沿轴向不断发生变化,而沿径向受力变化较小[15],因此,为简化计算,建立二维流场仿真模型,假设流场参数沿叶片径向均匀分布,选取导向器、涡轮各个叶片周边气体作为研究对象,并按照叶片型线分割流体,作为流场周期边界,并适当延长气体进口/出口边界长度,如图1所示。

图1 涡轮二维流场仿真模型Fig.1 Two-dimensional flow field simulation model of turbine
1.2 流场计算方程
由于涡轮叶片是运动的,因此,这里选用守恒型动网格流场计算方程[16],对于边界移动的任意控制体积V上的标量φ(质量ρ、速度u、能量E)的守恒型方程为:
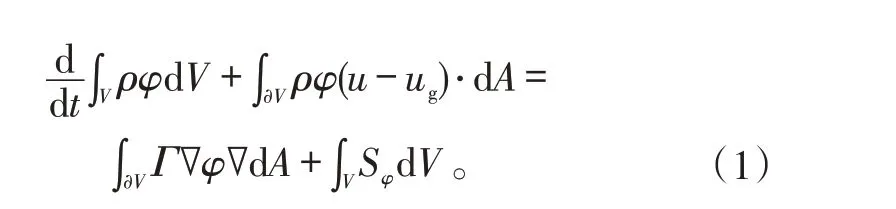
式(1)中:V(t)为空间中大小和形状都随时间变化的控制体积;ρ为流体密度;∂V(t)为控制体积的运动边界;ug为运动网格的运动速度;u为流体速度矢量;Γ为耗散系数;Sφ是标量φ的源项。
湍流模型采用计算精度比较高的且应用比较广泛的k-ε二方程模型:
k控制方程:


1.3 边界条件
本文选取涡轮在ω=1 500 r/min 转速下的仿真计算,仿真模型边界条件,如图2所示。

图2 涡轮二维流场计算网格及边界条件Fig.2 Calculation grid and boundary conditions of two-dimensional flow field of turbine
3)叶片壁面条件
假设气体与涡轮叶栅通道壁面之间均为“无滑移”条件,壁面粗糙度为常数0.5。
4)涡轮—导向器界面条件
由于涡轮在发动机工作过程中以ω速度运转,对应的流场仿真区域——涡轮叶片及其流场区域以圆周切向速度Vt上下做周期运动,由此在导向器出口与涡轮进口之间的燃气流通通道横截面时刻发生变化。为保证流场仿真过程中燃气质量守恒,在导向器出口与涡轮进口之间采用涡轮—导向器间滑动边界条件[16],即在涡轮流场区域与导向器流场区域的边界重合区域定义为内部区域,边界上其他区域(非重合区域)为周期区域,如图2所示。涡轮与导向器间滑动

涡轮中气体流动守恒就是从涡轮与导向器间重叠区域界面计算得到的。
5)周期边界条件
不管是导向器还是涡轮,其上叶片均为均匀分布,因此,这里选取各1个叶片及其周边流场区域作为仿真模型,叶片周边流场两侧边界设定为周期边界。
2 动网格流场仿真方法
本文采用有限体积法[17]的无结构化网格离散导向器—涡轮叶片周边流场区域,由于本文涡轮与导向器间滑动速度与气体进口速度均比较低,为提高计算精度,仅在流场壁面、周期边界、滑动界面采用加密网格,最终划得网格单元数为7 917,最小单元面积为6.554×10-4m2,最大单元面积为2.709×10-2m2,如图2所示。
在瞬态仿真计算中,流场控制方程的时间导数项用一阶向后差分公式得到:

式(11)中,δVj是控制体上面j在时间步Δt内扫出的体积。
3 仿真结果分析
本文仿真过程分2步:第1步,设定滑动边界条件的滑动速度为0,应用二阶迎风格式耦合算法求解流场控制方程,得到流场稳态仿真结果,作为第2步瞬态流场仿真的初始化值;第2步,启动导向器—涡轮间滑动边界条件,采用二阶隐式耦合算法计算瞬态流场控制方程。涡轮转速不同,时间步长也不一样,这里根据涡轮叶片通过1 个导向器叶栅通道跨距Δy的时间T来确定时间步长:

因此,涡轮叶片需要用18个时间步通过一个导向器叶栅通道跨距,这里选取流场仿真时间步长Δt为0.000 1 s,仿真时间为0.008 s,80 个时间步长,选取0.002 5~0.006 1 s 间计算结果进行分析,研究流场变量沿轴向位置变化趋势,每个流场变量在横截面上取平均值。
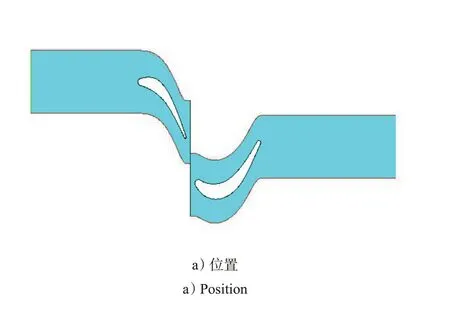
0.002 5 s 时,导向器流场区域与涡轮流场区域在滑动界面处重合,如图3 a)所示。
沿着流场周期边界线(导向器叶片和涡轮叶片轴向长度段)叶栅流场通道横截面逐渐减小,压力变化呈现先降低后升高,在导向器流场出口处达到最大值;在涡轮叶栅通道流动中,压力持续降低,低过出口气体压力P2,然后受P2的影响,增大到与外界压力平衡,如图3 b)所示。
气体在导向器叶栅通道流动过程中,速度马赫数持续增大,在滑动界面处,导向器流场出口速度等于涡轮流场进口速度,如图3 c)所示,在涡轮叶栅通道流动过程中,先呈现继续升高,而后由于受出口气体压力P2(背压)影响,气体速度呈现降低的变化趋势。

图3 0.002 5 s时涡轮流场位置及参数变化曲线Fig.3 Turbine flow field position and parameter variation curve at 0.002 5 s
0.004 0 s时,涡轮向下移动了0.161 6 m,如图4 a)所示。
气体在导向器叶栅通道流动过程中压力持续下降,在滑动界面处,达到最低值,由于受涡轮叶片阻力影响(导向器与涡轮流场出现非重合区域),气体压力在涡轮进口处出现跃升,如图4 b)所示,这是由于计算过程中保持气体参量守恒[18]引起的,而不是由于激波引起的。
气体压力在涡轮叶栅通道中持续降低,受P2的影响出现压力波峰振荡,并且导向器与涡轮流场出现非重合区域越大,振荡波峰越向上游扩展。气体速度在滑动界面处也出现不连续现象,并且在涡轮叶栅通道中也出现速度振荡,如图4 c)所示。这些流场参数在叶栅通道的变化趋势与一维等熵流动理论分析结果[19]是一致的。

图4 0.004 s时转子流场位置及参数变化曲线Fig.4 Turbine flow field position and parameter variation curve at 0.004 s
0.004 2 s 时,涡轮叶片到达最下端,0.004 3 s 时,涡轮叶片离开导向器叶片流场区域,下一个涡轮叶片进入导向器叶片流场区域。
4 结论
本文基于动网格二维流场仿真技术,采用流体动力学流场控制方程,应用有限元体积法仿真计算了航空发动机单级涡轮某一转速下气体流场分布,并对涡轮流场特性进行了分析,仿真过程及结果表明:
1)为提高流场仿真计算的收敛性和结果的精度,基于动网格的涡轮流场仿真分2步进行:首先,计算稳态条件下的流场仿真结果,将其作为下一步的初始化值;第2步,启动某一转速下涡轮转动引起的瞬态流场仿真。
2)在涡轮转动过程中,转子—静子间滑动界面时刻发生变化,引起界面处流场仿真参数发生阶跃,这是由仿真计算而非激波引起的。
3)气体在转子—静子叶栅通道流动过程中,流场参数变化主要受叶栅通道横截面积和进/出边界条件影响,仿真结果与一维等熵流动理论分析结果一致。
