弹性模型结合改进滑模控制器的无人机协同控制

2022-11-22范庆东

电光与控制 2022年11期

王琪，范庆东

(北京化工大学，北京 100000)

0 引言

过去的数年中，多智能体系统的编队控制技术已经得到广泛的研究和应用。无人机作为智能体的典型，能够实现的功能也愈发全面，然而，随着任务和环境要求的逐渐严苛，单无人机在执行任务时暴露出来的局限性越来越严重，而多无人机编队协同执行任务则能有效地避免此局限性。为了能够显著地提高执行任务的效率，增加系统的容错率以及执行任务的多样性，对于多无人机编队的研究逐渐成为研究的热点[1-3]。

目前,无人机编队的研究热点主要都集中在分布式控制方法上，其中,基于一致性理论的编队控制算法是一种典型的分布式控制方法，例如,文献 [4]提出了著名的Boid模型，但是该模型要求每个节点都需要满足分离、聚合和速度一致的要求，以保持编队的一致性。为了解决这些问题而提出的领航跟随法[5]是通过指定领航者的轨迹,并保持与跟随者之间的几何位置关系来保持编队的轨迹，但是领航跟随法因过度依赖显式领导者的存在而缺乏鲁棒性，一旦领航者出现问题就会造成群体失控。基于此，文献 [6]将领航者隐藏到无人机集群中，即不存在显性领导者，以便在必要时动态地指定领航者，从而提高编队控制的鲁棒性。研究者们同时还提出虚拟结构法[7]，在无人机编队的坐标系中指定一个虚拟点作为无人机编队轨迹的参考点，但是此方法需要大量的通信和计算而不适合分布式实现。为了结合不同控制策略的优点，有研究者提出了基于虚拟领航者[8]的编队保持方法，将领航跟随法与虚拟结构法相结合，用虚拟领航者代替实体领航者，提高编队抗风险能力，降低了由于领航者故障造成系统故障的风险。在实际的应用中，为了满足多无人机系统能够跟踪领航者或者已知的参考轨迹，针对系统的跟踪控制问题引起了学者们的广泛研究，并提出了滑模控制、自适应控制[9-10]和模糊预测控制[11-12]等算法。

滑模控制算法本质上是一类特殊的非线性控制，可以动态地根据系统当前的状态有目的地不断调整，而且对扰动具有优秀的适应能力，同时具有稳定性好及响应速度快等优点，广泛地应用于姿态控制[13]、编队控制[14]及轨迹控制[15]等不同方面。由于状态轨迹到达滑模面后，难以严格地沿着滑模面滑动，会产生严重的抖振现象，针对这一问题，以往的趋近律设计大多数都以不同的传统趋近律的有机结合来削弱抖振并加快收敛速度，但由于符号函数的存在，抖振现象很难消除[16-17]。所以各种自适应趋近律的设计也获得广泛关注，文献[18]在滑模面的设计中引入了模糊控制，可有效地抑制系统的抖振现象。而在文献[19]中提出一种遵循阻尼正弦特性的自适应趋近律，能使初始状态在极短的时间内到达期望的滑模面，同时忽略抖振对系统的影响。

受上述问题研究的启发，本文研究了多旋翼无人机编队的协同控制问题。本文所设计的方法主要有以下的贡献：首先，与文献[20]相比在弹性系统的基础上，引入编队相对误差，将无人机编队与传统弹性系统相结合，建立了多旋翼无人机的弹性系统模型；然后，设计了基于改进的指数趋近律的无人机编队滑模控制器，与传统趋近律的滑模控制器相比，加快了系统的收敛速度，有效地抑制系统的抖振现象；同时，该模型采用虚拟领航者对编队进行控制，降低了对领航者的依赖，有效地提高了编队的抗风险能力。最后，通过实际飞机的飞行试验验证了该编队控制器的有效性。

1 无人机编队协同控制系统设计

1.1 图论

本文分析的多无人机编队系统的通信拓扑结构采用有向图来表示。假设在由n架无人机构成的无人机编队系统中，通信网络为有向图G={Mi,W,A}构成，其中，点集Mi(i=1,2,…,n)表示无人机节点，W⊆{(i,j)∶i,j∈M,j≠i}，为边集。若Mi能获得Mj的信息，则wi j=1，否则wi j=0,wi j表示无人机节点之间的连接权重。由上可得系统的连接矩阵A=(wi j)∈Rn×n。此外，Ni为Mi的邻居集合，且Ni={j∈M∶wi j=1}。若Mi能获得Mj的信息，则Mj是Mi的邻居节点。

1.2 基于弹性约束的编队动力学模型

在一个弹性系统模型的基础上，考虑一个无人机编队，两个节点之间的相对位置约束称为编队弹性约束，编队的每一个节点都会有至少一个约束存在，以此保证编队信息流通，编队弹性约束强度用Kf表示。

同时定义由编队弹性约束引起的矢量力为编队约束力。对弹性系统模型分析后可知，通过调整合适的Kf值，不仅可以实现单无人机在编队中期望位置控制，还可以实现相邻两机之间的防碰撞功能。

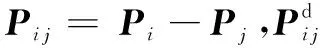
依据弹性系统建模，所有的无人机节点都取质量为m，无人机节点Mi受到的编队作用力只与无人机Mi本身和邻居无人机节点有关系，Ni为无人机Mi的邻居无人机集合，INi是Mi的邻居数为参数的对角矩阵，建立无人机编队系统模型为

(1)

整理式(1)可得

(2)

根据式(2)得

(3)

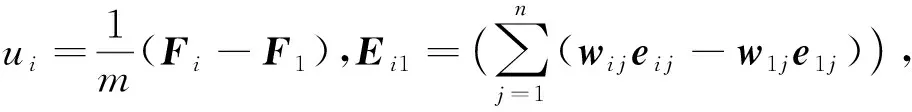
(4)

1.3 无人机编队协同控制器整体设计

依据所设计的弹性系统模型，为实现无人机编队的协同控制，设计了一个如图1所示的具有多级控制器的无人机编队协同控制系统，在该系统中，通过多个反馈控制实现无人机编队的协同控制。

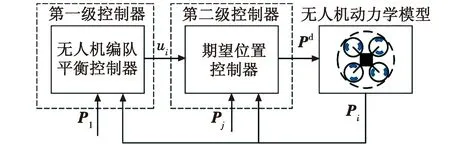
图1 无人机编队协同控制系统Fig.1 Cooperative control system of UAV formation

首先在第一级控制器中，依据设计的弹性系统模型实现无人机编队的平衡状态控制，基于弹性系统模型对编队进行受力分析，计算出为达到编队平衡，每个无人机的编队控制器的控制量；之后因无人机动力学模型通过接收位置信息对单机进行控制，故通过第二级的期望位置控制器通过控制量对单机进行受力分析，实现将无人机的控制量输出为期望的位置信息；最后将所设计的协同控制器接入现有的四旋翼无人机动力学模型中，实现对无人机编队的协同控制。

1.4 编队控制器设计

依据所设计的无人机编队系统模型，设计无人机编队控制器，采用一种改进指数趋近律的方式进行无人机的编队协同控制，首先针对系统的跟踪问题，设计滑模面为

(5)

式中，参数λ>0。

在对传统的滑模控制器的趋近律进行分析后，设计了一种利用改进指数趋近率的滑模控制器来实现无人机编队的协同控制，即

(6)

式中：D(s)=χ+(1-χ)e-β|s|;k，ε，α，β，χ为控制参数，且k>0，ε>0，0<α<1，β>0，0<χ<1 。

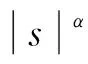
对式(4)～(6)进行整理计算后得无人机编队协同控制系统的滑模控制律为

(7)

以下通过Lyapunov函数对该滑模控制器进行稳定性分析，通过式(4)及式(5)可得

(8)

首先定义Lyapunov函数为

(9)

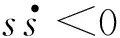
对式(9)求导后，将式(7)、式(8)代入计算后可得

(10)

1.5 期望位置控制器

通过编队控制器的计算后，作用在每架无人机上的控制量会驱动无人机在相应的方向上进行运动，完成无人机编队的平衡控制。为实现将控制量转换为位置信息并输出给无人机动力学模型，设计了如下的无人机期望位置控制器，已知控制器产生的控制量作用在第i架无人机上的合力为

Fi=mui+F1

。

(11)

假设作用在节点Mi上的编队约束力，其值与其邻居节点之间的距离误差成比例，表示为Fi j或者Fji，即

(12)

已知作用在Mi上的编队约束力为

(13)

在飞行过程中，为实现编队的稳定，作用在其上的合力应为零，即

(14)

将式(11)和式(14)代入式(13)得

(15)

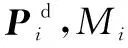
(16)

将式(15)代入式(16)可得

(17)

经过计算后得无人机期望位置控制器表达式为

(18)

式中，n为Mi的邻居无人机节点数。

由上节可知，每个无人机的编队控制方案通过编队控制器及期望位置控制器协同完成。通过改进滑模控制器，以及控制器输出量实现无人机编队的平衡状态控制，之后通过期望位置控制器实现将期望位置输出给无人机动力学模型，完成单机位置控制。

2 结果分析

2.1 数值仿真分析

首先采用数值仿真来验证所设计的改进指数趋近律控制器的有效性。考虑一个单输入单输出的系统，分别采用设计的改进指数趋近律及传统的指数趋近律、幂次趋近律来对比该控制器不同方面的性能，对比结果如图2所示。

图2 不同趋近律的阶跃响应Fig.2 Step response of different reaching laws

图2中，设计的控制器与传统控制器相比拥有更快的收敛速度，比指数及幂次趋近律快5 s左右到达期望位置；同时在接近期望位置时有效地降低收敛速度，从而有效地减少了超调的现象;与传统的指数趋近律相比还有效地避免了抖振现象。该控制器能够充分实现无人机集群的协同控制。

2.2 试验分析

在2.1节基础上，采用实机飞行的方式对所设计的基于弹性系统模型的无人机编队动力学模型进行试验分析。本文试验所采用的平台是基于光学定位系统和ROS机器人控制系统开发的无人机集群试验平台。通过Matlab/Simulink实现控制器的设计及无人机集群的协同控制；同时采用3架轴距均为150 mm的四旋翼无人机作为试验对象。试验中，通过亚毫米级的光学定位系统实时解算无人机刚体位置与姿态信息，通过ROS系统对无人机数据进行实时通信，以保证控制的实时有效。试验中所采用的通信拓扑如图3所示。

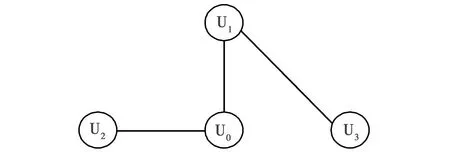
图3 通信拓扑Fig.3 Communication topology

试验采用虚拟领航者的实时轨迹对无人机编队进行控制，U1，U2为虚拟领航者U0的直接跟随者，U3为U1的直接跟随者，试验中所涉及的参数如表1所示。

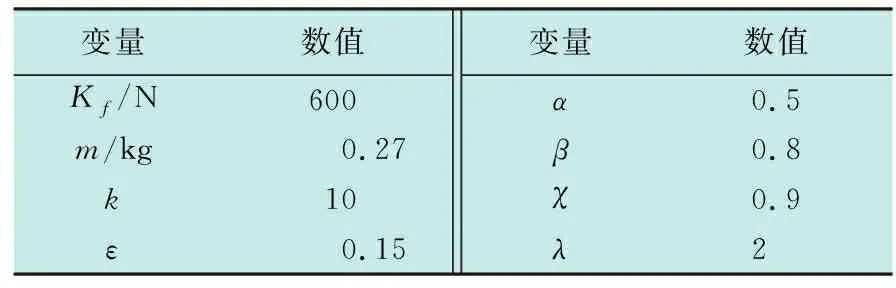
表1 参数表

首先，对于无人机编队的虚拟领航者设定期望的参考轨迹为

(19)

3架无人机之间保持固定的队形，跟随虚拟领航者的参考轨迹进行轨迹跟踪。如图4(a)及图4(b)所示，当无人机编队跟随轨迹控制时，有较快的收敛速度，控制延迟保持在0.5 s内，有着较好的实时性；同时，无人机在X轴及Y轴方向出现了不足0.2 m的跟随误差，同时在Z轴方向，实现了10 s内跟随到期望高度，而误差也保证稳定在了0.05 m之内。图4(c)则显示了滑模控制器的输出量u，表示了该无人机在该方向上的加速度变化值，在限制了无人机最大速度的情况下，该输出量也保证了无人机稳定地实现了向期望位置的运动。

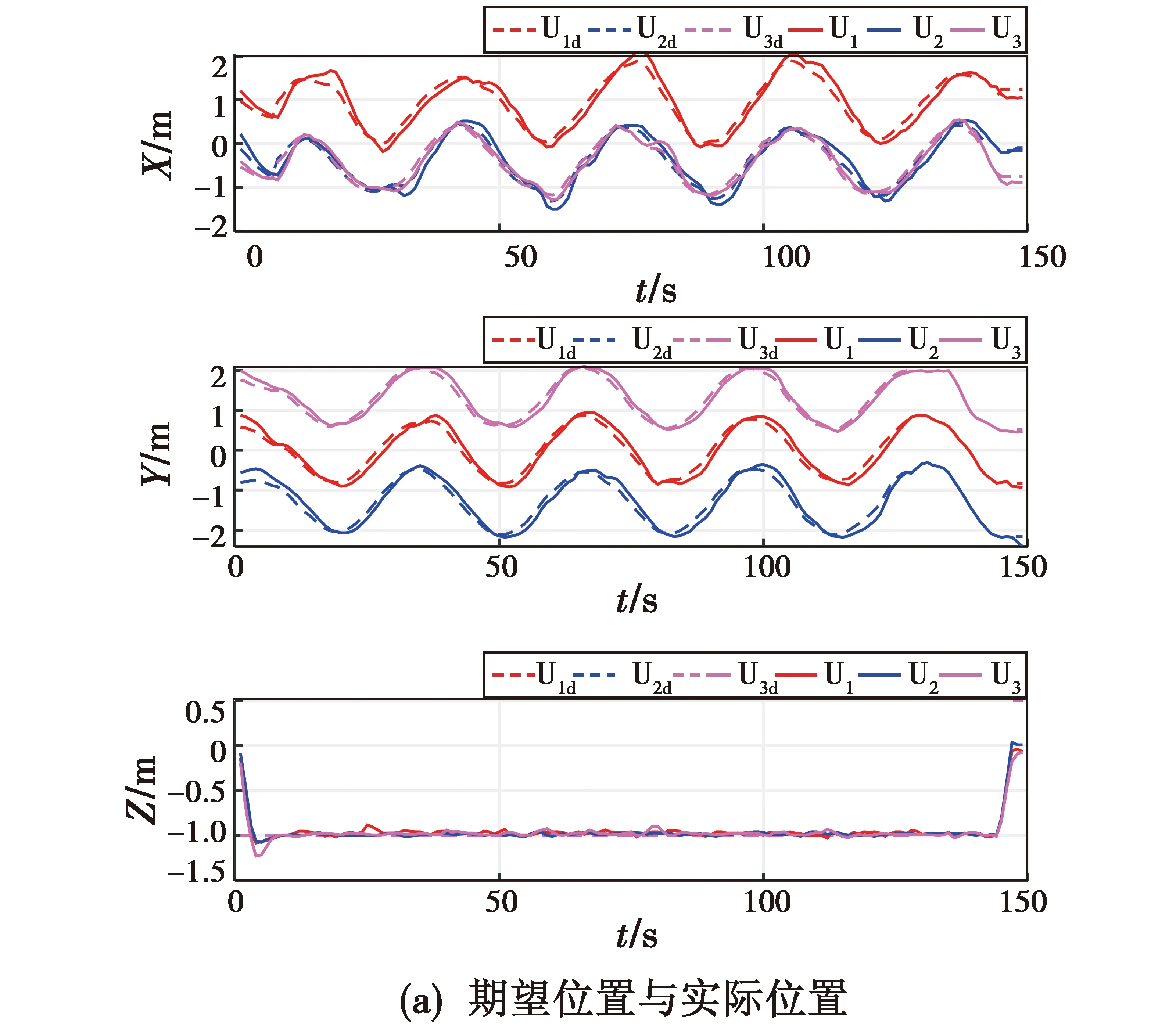
图4 轨迹跟随控制状态Fig.4 Control status of trajectory following

接着,为验证该控制还能够实现无人机编队的队形变换功能，让无人机编队实现如表2所示的队形1(三角形编队)到队形2(水平“一”字)之间的队形变换。

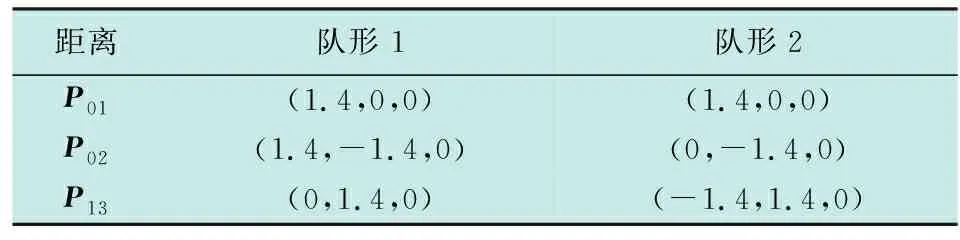
表2 无人机之间的期望距离

由于场地等原因的限制，仅实现无人机编队的单个方向的队形变换来验证该功能的有效性。图5所示为队形变换时，无人机在X轴方向上的控制量u的变化，当切换队形后，U2及U3在X轴方向上会以0.4 m/s2的加速度逐步降低速度向着期望位置进行运动，在9 s内到达期望位置。到达期望位置后，由于飞机本身的定位精度等干扰影响，控制器会输出一个0.05 m/s2的加速度来实现无人机的位置控制。在切换队形时，由于控制器的影响，在Y轴的控制输出量上会有一个不影响系统稳定性的单位阶跃。

图5 队形变换时的控制器输出量Fig.5 Controller output during formation change

图6为无人机的飞行轨迹。

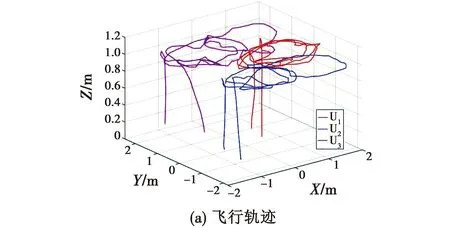
图6 飞行轨迹变换队形的状态Fig.6 Trajectory and the state of the formation

图6(a)所示为实现了无人机编队在切换队形的同时实现保持队形的目标，当无人机编队按照期望的轨迹运行时，给一个编队变换的指令，无人机能够向着期望的编队位置运动，同时不影响整个编队的轨迹运行。图6(b)所示为队形切换后，X轴方向的U2及U3期望位置有较大的变换，而无人机能够实时地跟随期望位置实现无人机编队的协同控制。