内导体偏心的准同轴线分布参数计算方法及应用
2022-11-22刘涛
刘 涛
(中国石油大学(北京) 信息科学与工程学院,北京 102249)
0 引言
均匀传输线的常见类型主要有平行双线、平行双板、同轴线以及微带线等,它是一种输送能量和传递信号的装置,由于其应用领域十分广泛而成为经久不衰的研究对象。因为只有确定传输线分布参数之后,才能建立传输线等效电路模型,进而才能研究线路参数分布性质和具体应用,所以在长线条件下不同类型传输线分布参数分析和计算方法始终是重要的研究内容之一。
一般情况下,均匀传输线单位长度上有4个分布参数,即分布电阻、分布电感、分布电导以及分布电容。它们的计算方法和数值大小与传输线的种类、形状、尺寸、导体材料性质以及周围媒质特性有关,正是因为这些复杂影响因素,致使精准地建立特定类型传输线的分布参数理论模型存在数学分析困难,因此时至今日仍然只有结构简单的理想同轴线、平行双线、平行双板类传输线建立了分布参数理论公式,有些类型的传输线(例如微带线)只是针对特定工况建立了经验公式,这种理论现状在某种程度上制约了新型传输线的研发和应用。(1)参见Pozar,D.M., Microwave Engineering,Third Edittion, John Wiley&Sons Inc, 2005.
近些年来,在石油开发领域,人们发明了利用井中套管(外导体)/油管或钻杆(内导体)构建长距离传输微波能的同轴线传输技术,依此传递井底信息或加热油层采油。在重力作用下,近千米长的内导体(即油管或钻杆)的轴线很难与外导体的轴线重合,这种油井同轴线在使用中出现内导体轴线偏心在所难免,这个生产实际使得内导体轴线存在偏心的复杂几何结构的准同轴线分布参数计算问题摆在了人们面前,并且亟待解决,因此本文建立内导体偏心的准同轴线分布参数数学模型,提出新的分布参数计算方法,不仅对丰富电磁波传输理论有益,而且对拓展传输线在地下石油开采工程中的有效应用具有实用价值。(2)参见王正旭:《井下射频加热技术基础研究》,硕士学位论文,中国石油大学(北京),2020年,第5页。
1 准同轴线截面几何关系及其场方程
本文在研究内导体轴线偏心的准同轴线分布参数计算方法时,没有采用人们常用的保角变换分析方法,而是基于珀扎尔(D.M.Pozar)提出的“场路结合”理论,在圆柱坐标系下分析问题。选取圆柱坐标系的轴与内导体轴线重合且其正方向与电磁波传输方向一致;用表示外导体轴线相对于内导体轴线的平移距离,称之为偏心距;假设偏心距不大,即有e 图1中r0是内导体中心到外导体内壁面的距离。根据斜三角形余弦定理,可得如下几何关系式, (1) (2) 图1 准同轴线任一截面示意图 当偏心距e不太大时,在圆柱坐标系下有 (3) (4) (5) 现取一段1m长的准同轴线,用S表示同轴线的横截面积,设同轴线两导体间电压为Uae±jβz、电流为Iae±jβz,则可知在1m长同轴线上的时间平均磁储能为: (6) 根据电路理论可得: (7) 因此,可得单位长度电感L(单位为亨/m)为: (8) 进而可得本文研究的准同轴线单位长度电感为: 因为, 所以,可得 (9) 根据经典理论知道,在1m长同轴线上的时间平均电储能为: (10) 根据电路理论可得: (11) 因此,可得单位长度电容C(单位为法/m)为: (12) 进而可得本文研究的准同轴线单位长度电容为: 因为, (13) 根据传输线电感、电容的几何因子之间互为倒数的关系,式(13)也可以用下式表达: (14) 根据电磁场理论,金属导体的电导率为有限值时产生的单位长度功率耗散为: (15) 在式(15)中,假设H是内导体围线c1、外导体围线c2的切线分量,c1+c2表示在导体边界上的积分路径;RS表示导体的表面电阻,即有 (16) 式中的σ是导体的电导率,δ表示趋肤深度。 根据电路理论又可得: (17) 因此,可得单位长度串联电阻(单位为欧/m)为: (18) 进而可得本文研究的准同轴线单位长度串联电阻为: 因为, 所以,可得 (19) 根据电磁场理论知道,在有耗介质中,单位长度同轴线中的时间平均功率损耗为: (20) 在式(20)中,ω表示角频率;ε″表示填充介质的复介电常数的虚部,即有 ε=ε′-jε″=ε′(1-jtanδeff) (21) 式中的tanδeff=ε′/ε″是损耗角正切。 根据电路理论可得: (22) 因此,可得同轴线单位长度的并联电导(单位为西门子/m)为: (23) 进而可得本文研究的准同轴线单位长度并联电导为: 即有, (24) 根据特性阻抗Z0的定义式: (25) 再应用本文建立的分布参数R、L、C、G公式计算,便可求得内导体存在偏心距的准同轴线特性阻抗Z0。 现在假设准同轴线的损耗很小,即满足R≪ωL、G≪ωC时,可得 (26) 将前面的式(9)、式(13)或式(14)联立,可容易地得到本文研究的内导体存在偏心距的准同轴线特性阻抗Z0为: (27) 式(27)中,εr表示同轴线导体间填充介质的相对介电常数,其它符号意义同前。 表1列出了同轴线经典解析公式与本文建立的存在小偏心距的准同轴线解析解对比,从表中结果可见,当同轴线的偏心距e=0时,本文诸式都能够恢复到同轴线的经典公式,这证明本文解析解在理想条件下是正确的。(5)参见Pozar,D.M., Microwave Engineering,Third Edittion, John Wiley&Sons Inc, 2005. 表1 本文的准同轴线解析解与经典公式(1)的对比 中国学者甘本袚、陈梅泉基于保角变换和系列简化方法曾经建立了内导体偏心的同轴线特性阻抗计算公式,并且陈梅泉在其文章中还给出了验证算例。(6)参见甘本袚:《微波传输线设计手册》,北京:人民邮电出版社,1981年,第334—347页。现在,应用陈梅泉等人的资料验证根据本文分布参数建立的特性阻抗理论公式。 陈梅泉给出的特性阻抗公式: (28) 甘本袚给出的特性阻抗公式: (29) 应用本文分布参数建立的特性阻抗公式,即式(27): 现将陈梅泉等人的验证算例数据代入上述三个公式中,可得计算结果如表2所示: 表2 应用前人资料对本文理论的验证结果 从表2所示验证结果可以看出,应用本文分布参数公式建立的特性阻抗解析解与前人给出的理论公式结果吻合良好,结果证明本文建立的分布参数公式是正确的,本文的分布参数解析解物理概念清晰、表达式简洁,计算结果的精确性与前人公式基本相同。 应用“场路结合”方法,研究了内导体存在偏心的准同轴线中电磁波传输问题,建立了内导体存在偏心的准同轴线分布电感、分布电容、分布电阻、分布电导计算公式,弥补了这方面的理论不足。本文通过两种方式验证了本文理论的正确性和较好的精确性。①当同轴线内导体的偏心距时,本文诸式都能够回复到理想同轴线的经典公式,证明本文理论在理想条件下是正确的。②应用前人公开发表的文献资料,对应用本文分布参数建立的准同轴线特性阻抗解析解与前人提出的两个特性阻抗公式进行了计算对比验证,得到了本文解析解与前人公式结果非常吻合的结论。 本文提出的分布参数计算方法物理概念清晰、表达式简洁,计算结果的精确性较高。研究结果不仅进一步丰富了传输线分布参数理论,而且为微波加热开采石油工程优化设计、合理构建地下井筒同轴线提供了理论分析和计算方法。
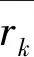

2 准同轴线分布参数计算方法
2.1 准同轴线单位长度电感的计算
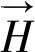

2.2 准同轴线单位长度电容计算

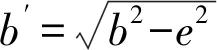
2.3 准同轴线单位长度串联电阻计算
2.4 准同轴线单位长度并联电导计算

3 应用分布参数计算准同轴线特性阻抗
4 理论公式的验证与分析
4.1 本文解析解与理想同轴线公式的对比验证
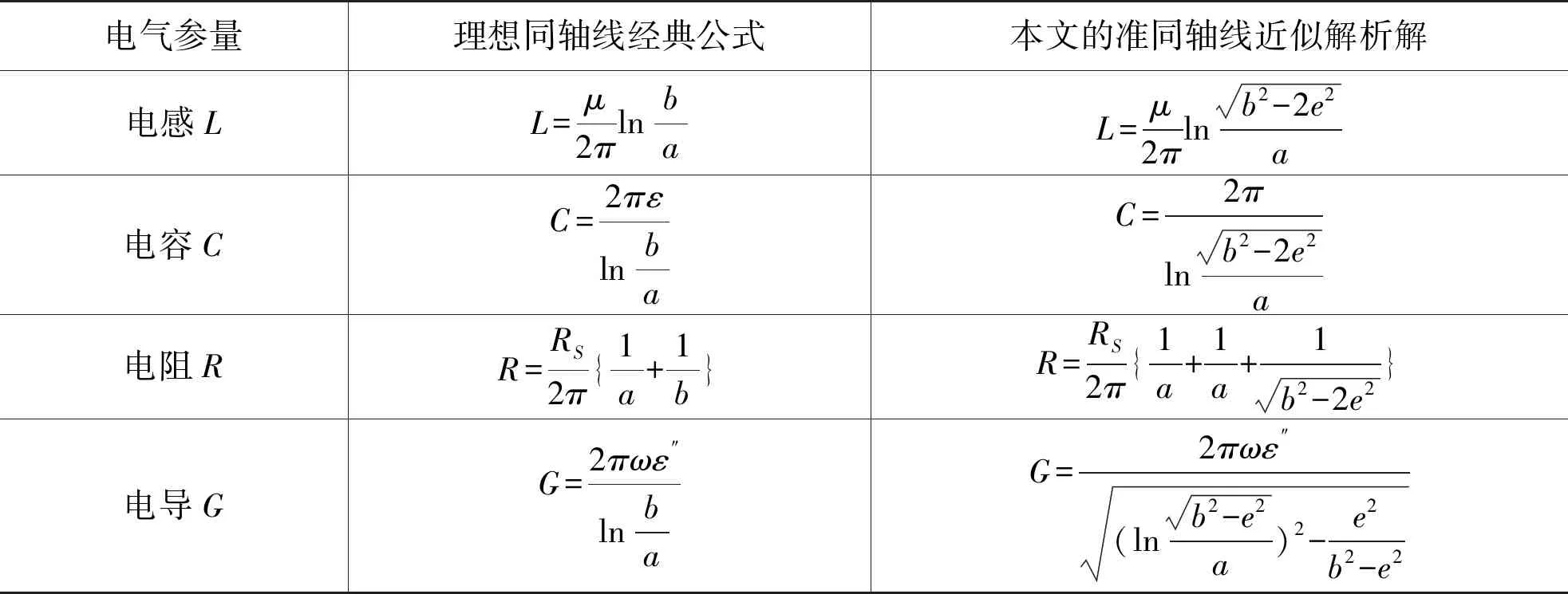
4.2 本文解析解与前人理论的对比验证
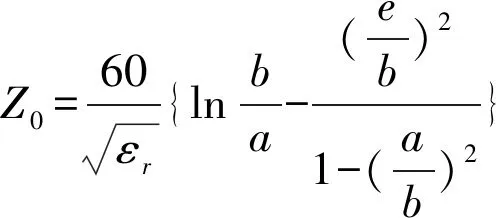

5 结论
