基于卷积神经网络的管道缺陷量化识别方法

崔国宁，杨理践，耿 浩，刘屹然

(1.沈阳工业大学信息科学与工程学院，辽宁沈阳 110870；2.国家管网集团油气调控中心，北京 100013)

0 引言

长输油气管道主要采用管道漏磁检测技术检测管道缺陷位置及大小。由于管线较长，检测的数据量较大，且缺陷的识别主要采用人工判读的方式，耗时耗力且容易造成误检、漏检，因此亟需开展智能化缺陷识别方法，提高缺陷的识别效率。

针对管道缺陷的智能化识别方法，各位学者已经开展了大量研究。姜慧明等[1]利用梯度融合方法将梯度图融合到U-Net编码器，增加了特征的复用性。文献[2]提出了一种利用数据样本之间的相似度获得拉普拉斯矩阵特征信息，清洗错误标记的数据点的方法，获得了更精确的结果。文献[3]提出了一种基于多特征视图的浅层卷积神经网络，实现了自动驾驶汽车的道路区域精确分割。徐富勇等[4]、李旺枝等[5]直接将图像输入到CNN中，其算法能够自动学习图像特征，减少人工特征提取过程。曹辉等[6]为了提高管道焊缝法兰组件的识别精度，采用深度学习网络的识别方法，对漏磁检测的图像进行识别。王竹筠等[7]通过改进SSD网络模型的图像识别算法，对管道漏磁图像数据实现了自动识别各种焊缝及缺陷定位。文献[8]提出了一种基于patch-wise M-net结构的图像自动分割网络，实现了更大的细节保留。邓志鹏等[9]、高鑫等[10]通过变形卷积网络结构，实现提取密集区域中的目标特征，有效提高了识别精度。

本文CNN包含4个卷积层、4个池化层、3个全连接层和1个输出层，采用Adam优化器和MAE损失函数，线性输出训练结果，可实现批量识别管道缺陷，输出缺陷尺寸参数。

1 管道漏磁内检测原理

管道漏磁内检测是利用永磁铁通过钢刷将管道磁化，达到饱和状态或接近饱和状态。若管壁内部及表面完好无损伤，则磁感线会在管壁中平行穿过，管壁表面几乎无磁场的突变；若管壁表面或内部有缺陷，缺陷边界处磁导率发生变化，磁感线流向发生变化，部分磁感线会溢出管壁，在空气中绕过缺陷进入管壁，在缺陷处的管壁表面形成漏磁场。检测原理如图1所示。

利用磁敏传感器获取管壁表面漏磁场的磁通量，计算机对采集的信号分析处理，计算出缺陷的形状与尺寸，评估缺陷的危害程度。

1.1 漏磁信号数据特点

目前，为了全面获取完整的缺陷信息，主要采用三轴传感器检测磁场信息；缺陷处漏磁场信号包含径向、轴向、周向3个分量，如图2所示。

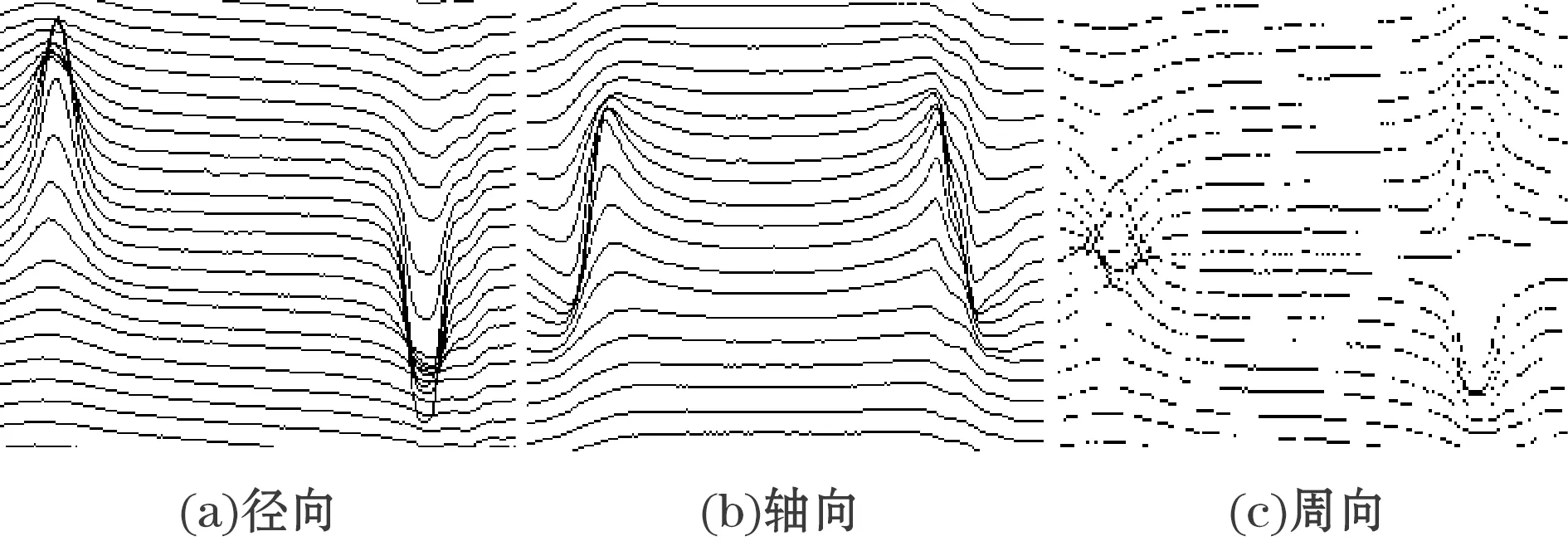
图2 管道缺陷漏磁信号

对于相同宽度和深度的缺陷，随着长度的增加，径向分量的峰峰值间距增大，幅值减小，信号曲线变化趋于平稳；轴向分量的峰谷值间距增大，幅值减小。因此可通过径向分量峰峰值间距和轴向分量峰谷值间距及幅值计算出缺陷长度。

对于相同长度、宽度，不同深度的缺陷，随着深度的增加，径向分量峰峰值和轴向分量峰谷值均增加，具有较好的线性关系。缺陷漏磁场信号的三轴分量共同决定了缺陷量化结果。

1.2 漏磁信号数据集建立

为了提高缺陷的识别精度，首先建立准确且适用于识别的数据集。采用管道漏磁内检测器采集的实际管道的缺陷处漏磁场三轴信号分量，进行数据集的建立。

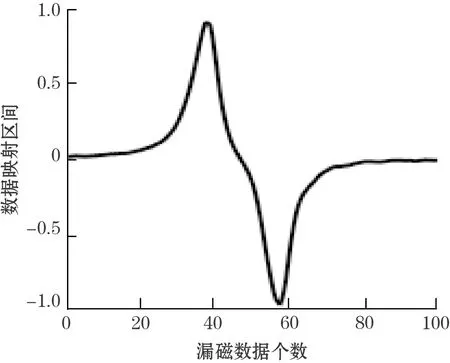
本文采用Φ1 016拖拉实验数据，检测探头环向排列，选取覆盖缺陷检测范围的20个探头的检测数据作为数据源，每个探头选取100个数据的检测长度，包含3个分量的检测数据，每个缺陷数据为60×100的二维矩阵。3个分量的检测数据的量级差异较大，对数据进行归一化处理，将所有数据同比例映射到区间[-1,1]，如图3所示。

(a)径向

2 基于卷积神经网络缺陷识别算法

2.1 卷积神经网络

卷积神经网络(convolutional neural networks，CNN)是一类包含卷积计算且具有深度结构的前馈神经网络，可根据误差自动优化提取数据特征，易于实现对数据的智能识别。

卷积神经网络对于任意输入的数据，经过卷积层中的卷积核提取特征的操作，输出多个特征图。特征图是由像素值构成的二维矩阵。卷积操作后输出的大量二维特征矩阵，引入池化层的池化操作减小产生的特征数据量，再通过若干全连接层计算出目标结果。

2.2 神经网络模型建立

为了实现管道缺陷尺寸的识别，提出了一种改进的卷积神经网络模型，如图4所示，其中主要包含4个卷积层、4个池化层、3个全连接层和1个输出层。

图4 卷积神经网络结构

2.2.1 卷积层

卷积层的作用是通过卷积操作提取输入数据的特征，其中包含3部分：卷积、加偏置和非线性激活。卷积神经网络中第一个卷积层通常提取的特征比较明显，后一个卷积层可进一步提取较为复杂的特征，用于识别的数据或图像通常较复杂，因此需要多个卷积层提取数据特征，实现更高精度的识别结果。

卷积操作的表达式为

(1)

式中：m与n为卷积核行列的大小；y为输出的特征数据；wij为用于训练的卷积核参数；xij为卷积核参数对应的输入数据。

非线性激活是将卷积操作后输出的特征数据输入到非线性激活函数中，实现非线性化。文中采用ReLU激活函数，有效改善神经网络训练中梯度消失的问题。表达式为

f(x)=max(0,x)

(2)

2.2.2 池化层

池化层又称为非线性降采样层。经过卷积层输出的特征数据量很大，对网络的训练效果影响较大，需要对卷积操作后的数据进行降维处理。

通过池化后，会有少部分信息丢失，但能根据池化类型保留主要的特征数据。同时池化操作能有效提高神经网络对输入畸变的鲁棒性。

2.2.3 全连接层

输入数据经过多个卷积操作与池化操作后，数据量较少且均为保留的更高层次的特征数据，根据非线性回归的原理计算得到管道缺陷尺寸。

2.2.4 输出层

输出层采用线性方式输出训练结果，训练结果与样本标签对比，根据误差大小反馈结果，重新优化模型中的权重值，使误差达到最小。

2.3 模型训练方法

网络模型采用全局监督训练的方式进行训练。优化器采用Adam算法，即自适应时刻估计方法，能计算每个参数的自适应学习率。损失函数采用MAE即平均绝对误差损失函数，表达式为

(3)

式中：MAE为模型预测值f(xi)与样本真实值yi之间差距的平均值。

模型训练过程中的各参数根据梯度下降优化算法和损失函数实现更新优化。

3 实验与结果分析

模型训练的数据为管道漏磁内检测器若干缺陷的油气管道的检测数据，各类内外伤共180个，120个缺陷数据用于模型训练，45个缺陷数据作为模型的验证集，剩余15个缺陷数据用于测试模型训练结果，检验模型的识别精度。

3.1 不同算法对比分析

模型训练过程中采用不同的优化器和不同的学习率，对比模型训练结果，观察模型的收敛速度以及模型能达到的最小损失值。优化器采用常见的随机梯度下降法SGD和自适应梯度下降法Adam，学习率分别取0.02、0.01、0.005和0.001，训练损失值的收敛情况如图5所示。

(a)SGD_0.02

从图5可知，模型训练过程中根据不同的迭代函数与学习率，损失值的收敛情况不同。在相同学习率下，自适应梯度下降算法(Adam)对模型的收敛效果明显优于随机梯度下降算法(SGD)。对于相同的迭代函数，学习率的大小对模型的收敛效果影响大，图中模型整体上处于收敛状态，学习率较大时，模型的稳定性较差，振荡较明显，导致模型的收敛速度较慢。随着学习率的减小，模型收敛趋于稳定，振荡减弱，模型整体收敛速度加快；学习率过小时，模型的收敛更加稳定，模型始终处于收敛状态，无振荡情况，但模型的收敛速度随着学习率的减小而减慢。选取合适的学习率至关重要。对比训练结果，当采用自适应梯度下降法，学习率取0.005时，训练效果最佳。

3.2 实验误差分析

实验采用15个缺陷数据测试模型训练结果，每个缺陷数据均包含径向、轴向、周向3个分量，分别对长宽深进行识别，每个缺陷的长宽深均不完全相同。表1为缺陷实际长度、模型识别长度与误差的数据表。

表1 模型测试缺陷长度与误差 mm

从表1可知，不同缺陷的长度相同，但缺陷的宽度与深度不同时，对缺陷长度的识别结果也不同。模型总体的识别误差较小，误差范围为0～7 mm，识别精度满足工程应用需求。

模型对缺陷的识别中，对同一缺陷采用的训练数据完全相同，保证缺陷长宽高所受的影响一致，但对于网络输出的识别结果(长宽高)各不相同，因此无法通过一个模型同时实现对管道缺陷的长宽高的识别。采用3个结构相同的网络模型，分别对缺陷的各分量进行识别，模型测试缺陷宽度与误差如表2所示。

从表2可知，对于缺陷的宽度识别，相同宽度的缺陷，由于缺陷的长度与深度各不相同，对相同宽度缺陷的识别结果不同。总体来说，模型识别结果与缺陷真实尺寸误差较小，误差范围在0～19 mm，满足工程应用需求。

表2 模型测试缺陷宽度与误差 mm

对于缺陷深度的识别结果如表3所示。

表3 模型测试缺陷深度与误差 mm

从表3可知，针对缺陷的深度，模型识别结果与真实值误差较小，误差主要在0～5 mm范围。该识别精度基本满足工程应用需求，但由于管壁壁厚相对较小，对于提升缺陷深度的识别精度依然存在较大需求。

4 结论

建立CNN模型和管道缺陷处漏磁信号数据库，训练及验证模型对管道缺陷尺寸的识别能力，得出结论：本文提出的CNN模型采用的Adam优化器相比于SGD优化器，缺陷识别误差下降迅速，模型识别精度高，效率更高；学习率为0.005时，模型训练误差更小，精度更高，收敛速度更快；CNN对漏磁信号数据的识别精度较好，对于不同缺陷的识别精度相似，满足工程应用需求。