考虑最大线应变理论的多重破坏机制PMC强度模型

李晓光，周春雷，范栋珏,3，张力天，郑益武

(1.北京科技大学，北京 100083；2.军委机关事务管理总局工程代建管理办公室，北京 100082；3.北京科技大学顺德创新学院，广东 佛山 528399)

深部开采条件下，高应力、强扰动诱发的岩石破坏过程表现出明显非线性行为和破坏机制的转化特征，在此过程中岩石伸长、剪切及压密屈服等多种破坏机制共生。不同围岩下岩石表现出不同的破坏模式，岩石在拉力状态或者较低压力水平下表现为拉破坏，随着压力逐渐上升，岩石破坏模式从拉破坏向剪切破坏过渡，深部较高应力水平下岩石破坏模式从常规剪切破坏向孔隙坍塌型破坏转化。因此，岩石表现出拉破坏、剪切破坏和压剪屈服等多种破坏模式过渡的现象。

PAUL[1-2]在Mohr Coulomb模型基础上考虑中间主应力的影响，提出了包含三个主应力的表达式，并从单轴压缩、统一三轴(各向同性)伸长和单轴伸长的应力状态确定了三个参数常量。MEYER等[3]将其发展为PMC强度准则，针对岩石材料的破坏机理转化特征，以PMC模型为基础，讨论了十二边形PMC破坏面的形状，通过拟合两个破坏平面来描述非线性破坏面，发展出十二面椎体PMC模型，其模型能够观察到随着平均应力的增加破坏面的形状变化，可以表征岩石材料随应力条件上升由拉断破坏向剪切破坏转变的特征。在材料参数方面，MAKHNENKO等[4]提出了一个平面拟合方法，依据数据点和破坏面的正交距离平方和最小值进行求解；ZENG等[5]提出了采用最小二乘法拟合参数；DEHLER等[6]提出了简化的PMC模型，假设拉伸和压缩条件下摩擦角相同，使十二边形PMC减少了两个参数，仅包含四个参数。

本文研究以最大线应变理论、PMC过渡型准则为理论基础，拟合现场、室内试验数据，提出适合深部岩体破坏模式过渡特征的强度理论，并能够揭示岩体低强度破坏内在机理。

1 PMC理论

PAUL[1-2]在1968年考虑中间主应力的影响，提出了PMC模型；MEYER等[3]在2013年将其发展为PMC强度准则，其主应力的表达式见式(1)。

Aσ1+Bσ2+Cσ3=1

(1)

式中：A、B、C为材料常数，表达式见式(2)～式(4)。当B=0时，式(1)变为MC强度准则。

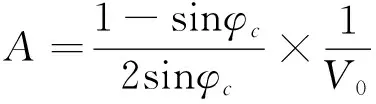
(2)

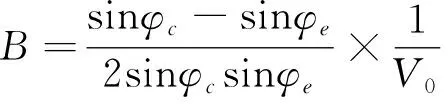
(3)

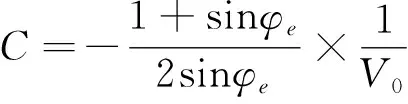
(4)

式中：φc、φe分别为压缩时内摩擦角和伸长时内摩擦角；V0为理论三轴抗拉强度。

将三个参数代入式(1)，用两个内摩擦角和顶点表示见式(5)。

(5)

PMC破坏准则在主应力空间构建了一个有共同顶点V0的破坏面，PMC准则利用岩石材料在压缩和拉伸时摩擦角的不同来考虑中间主应力的影响，是一个包含三个主应力的多轴线性破坏准则，包含的三个材料参数可通过岩石常规三轴实验得到，PMC模型破坏包络线如图1所示。

图1 PMC模型破坏包络线Fig.1 PMC model failure envelope

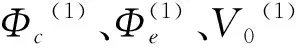
图2 十二边形PMC模型Fig.2 Dodecagonal PMC model

2 考虑最大线应变强度的三段线强度准则

2.1 最大线应变理论在岩石破坏模式分析中的应用

岩石在不同围压作用下表现出不同的破坏模式，在拉力作用状态或者较低压力水平下岩石主要以拉破坏为主，而不是以剪破坏为主。然而，无论是使用MC模型还是PMC模型，都只包含压缩剪切和纯剪切应力条件下的破裂准则，而对岩石拉伸剪切条件下的破裂准则没有表述[7]。因此，采用MC准则对拉应力或低应力水平下岩石破坏进行计算往往会带来较大的误差。针对这一现象，PAUL[8]将MC准则的单斜直线改为一条斜直线和一条与单轴拉伸应力圆相切的垂直线，形成双段线性强度曲线，即拉伸截断准则，截断后破坏准则如图3所示。其中，σt为实测抗拉强度，σt0为莫尔强度包络线计算所得的抗拉强度。由图3可以看出，AB段岩石同时受到拉应力和剪应力的作用，此时其破坏仍以拉破坏为主。然而，十二边形PMC模型能够表征岩石材料随应力条件上升由拉断破坏向剪切破坏转变的机制，但无法对拉伸剪切作用下岩石的破坏机制进行表征。因此，需要对岩石的拉剪破坏准则进行研究，并获得其与PMC强度理论的衔接关系。

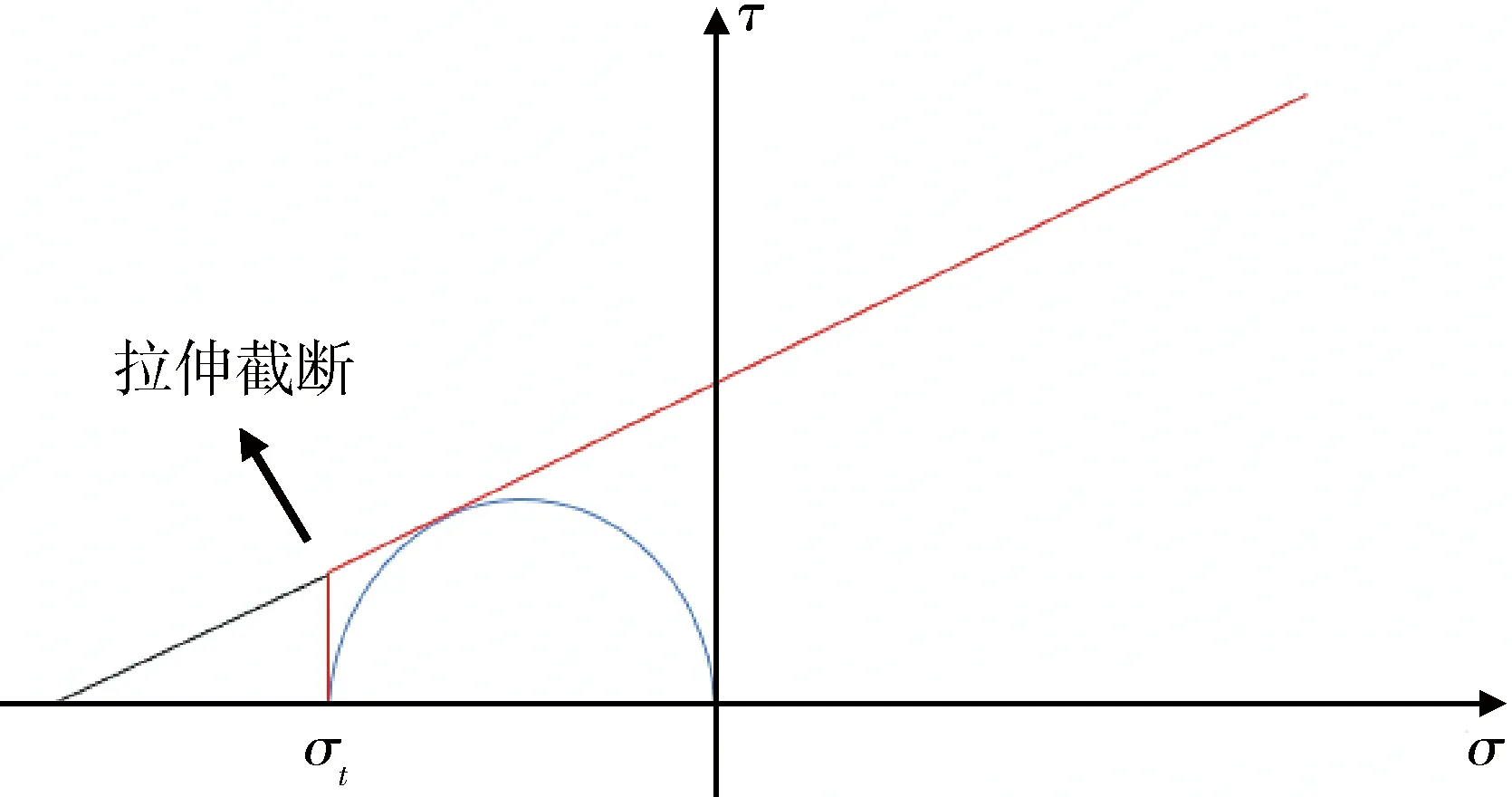
图3 拉伸截断示意图Fig.3 Schematic diagram of stretch truncation

许多学者对拉伸剪切条件下岩石的强度准则进行了研究，获得的模型大致可以分为双曲线模型[9-12]、抛物线模型[9,11,13]以及基于Hoek-Brown准则的模型[14-15]。但相对来说这方面的研究仍然较少，试验数据不足，导致目前得出的拉剪本构模型与破坏准则缺乏充分的依据。STACEY[16]利用最大线应变理论试图预测南非深层块状石英岩的脆性破坏机制，研究表明，对于显示线性变形行为的材料，破坏发生可能考虑与拉伸应变有关，岩石的拉伸应变可由广义胡克定律进行计算，见式(6)

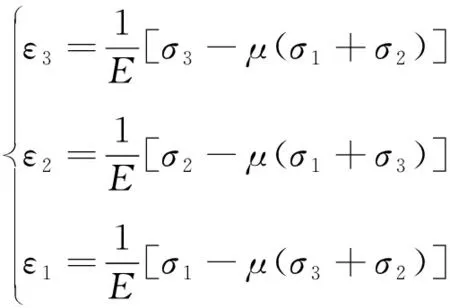
(6)

式中：μ为泊松比；E为弹性模量。根据最大线应变理论，当最小主应力处的应变大于临界应变时，岩石就会发生拉伸破坏。当ε3<0时，试样发生拉伸应变；当ε3>0时，试样发生压缩应变。

2.2 考虑最大线应变的三段线性PMC模型的提出

在十二边形PMC模型的基础上，添加考虑最大线应变理论的破坏面P3，提出同时考虑拉剪破坏和压剪破坏的三段强度公式，该模型用三个主应力可以表示为式(7)。

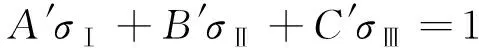
(7)

式中，A′、B′、C′为材料常数。

对于破坏面P3(最大线应变理论)，根据广义胡克定律，可以得到破坏条件见式(8)。

ε1orε2orε3=εc

(8)

式中，εc为临界应变，表达式见式(9)。

εc=-σt/t

(9)

式中：σt为抗拉强度；μ为泊松比；E为弹性模量。

当σⅢ-μ(σⅠ+σⅡ)<0时，岩石处在拉伸破坏及拉伸破坏至剪切破坏过渡段。根据最大线应变理论，当εⅢ=εc时，岩石发生拉伸破坏，符合式(10)。

-σt=σⅢ-μ(σⅠ+σⅡ)

(10)

由式(9)和式(10)可得式(11)。

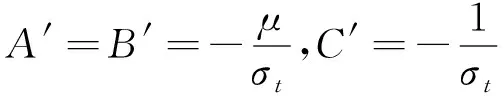
(11)

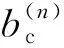
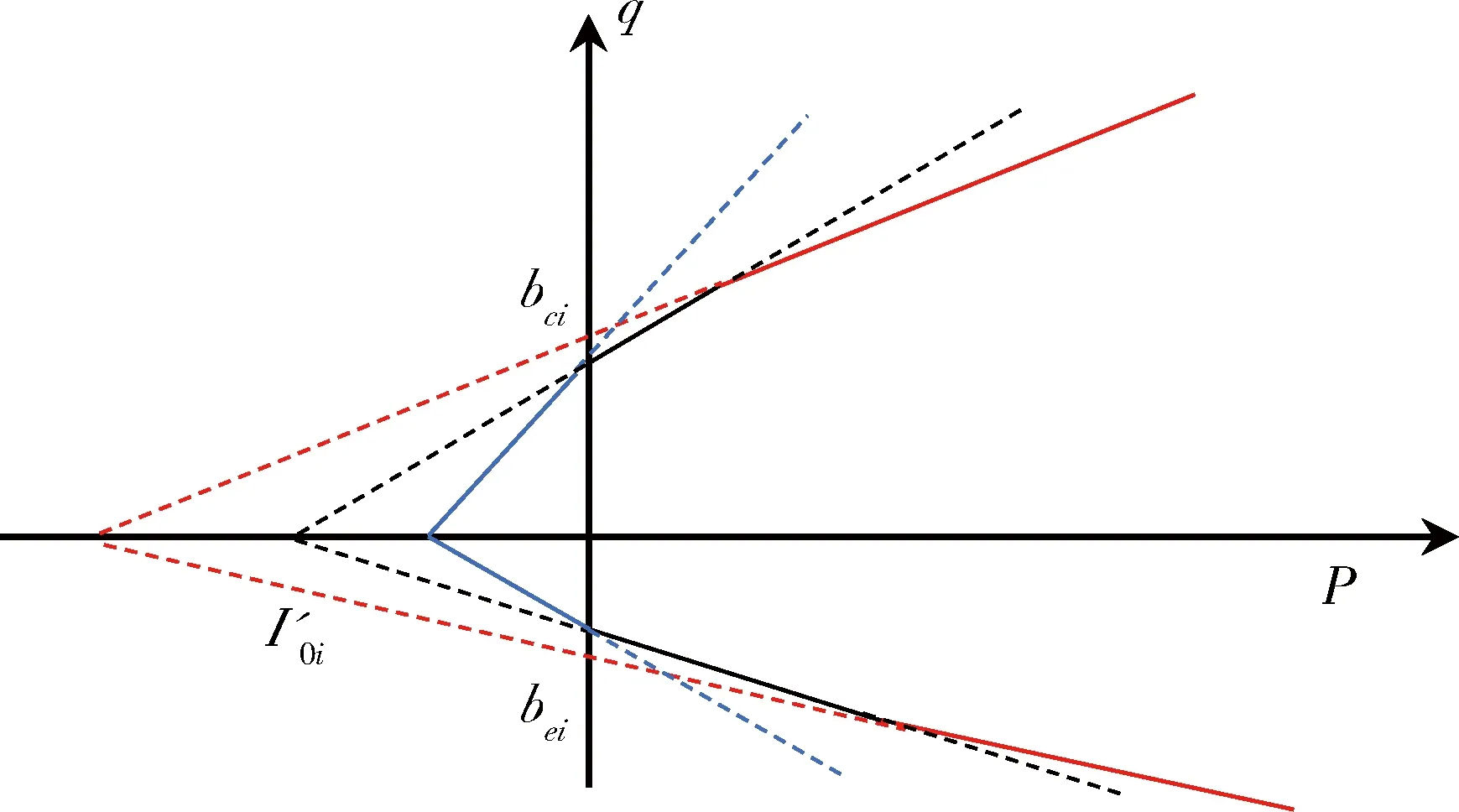
图4 最大线应变理论p-q平面示意图Fig.4 p-q plane diagram of maximum linear strain theory

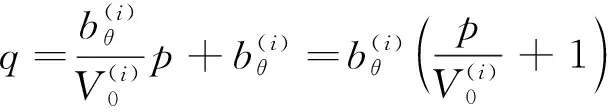
(12)

采用分段线性方式拟合破坏曲线，获得考虑最大线应变的PMC强度公式，在p-q平面内，其公式可以表示为式(13)。

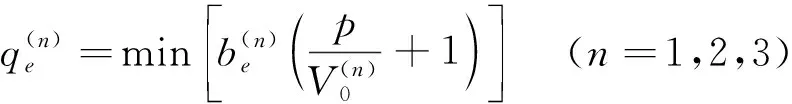
(13)

式中，n为破坏机制序号。

当n=1时回归为常规PMC模型，n=2时为十二边形PMC模型，n=3时为通用多机制破坏模式下强度模型。若n=1，且bc=be时，回归为常规Mohr-Coulomb强度公式。

2.3 三段线性PMC模型参数获取

ZENG等[5]基于在p-q平面的应力不变量关系的转换提出了一种新的拟合方法。本文基于该方法进行三段线性PMC模型参数获取方式的推导。在一个π平面中任何给定的应力状态都可以在柱坐标中(rθ，θ，ρ)表示。图5为当p=0时，PMC破坏面在π平面中的示意图。

图5 当p=0时，PMC破坏表面在π平面示意图Fig.5 Schematic diagram of PMC failure surface inπ plane in polar coordinate and orthogonal coordinate system when p=0

截距bθ需要进行定义，bθ和rθ之间建立一种联系。破坏包络线y=kx+rc在直角坐标系中用rθ和θ表达式见式(14)。

rθcosθ=k×rθsinθ+rc

(14)

在π平面中k是直线的斜率，则rθ见式(15)。

(15)

在任何π平面中，rθ与qθ的关系可以通过第二应力不变量J2得到式(16)。

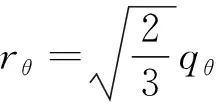
(16)

多轴线中qθ=bθ，轴对称压缩线中qθ=bc，轴对称伸长线中qθ=be。因此rθ可以表示为式(17)

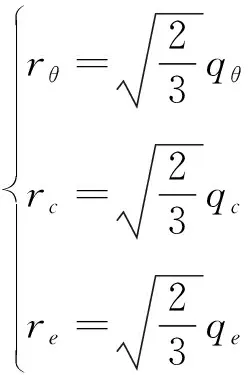
(17)

将式(17)代入式(15)中，可以得到bθ，见式(18)。

(18)

在p-q平面中，式(18)代表截距bθ的一种函数关系，未知变量k需要确定。在π平面中，破坏线经过轴对称伸长点(rθ=re,θ=60°)，式(15)可以表达为式(19)。

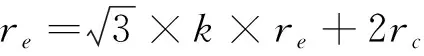
(19)

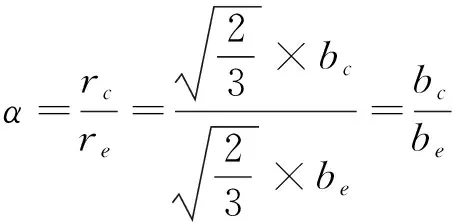
(20)

将式(20)代入式(19)，可得式(21)。

(21)

得知bθ和k的表达式，p-q平面中PMC准则的一般方程式(21)可以表达为式(22)。

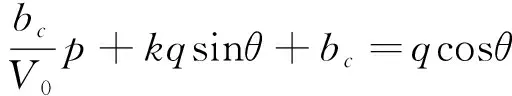
(22)

根据式(22)，可以使用轴对称压缩、伸长和多轴测试数据，通过每种条件下的θ和来构建一个线性方程组，θ在几何学上等于洛德角，但也会有差异。最初洛德角的定义是从-30°到30°，但是坐标系统中是从0°到360°，但是0°到60°已经足够用于各向同性的表达。θ=0°是轴对称压缩，θ=60°是轴对称伸长，多轴应力状态的θ值可以通过主应力计算得到式(23)。

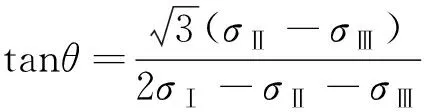
(23)

轴对称和多轴条件下强度数据表示为(σⅠ,σⅡ,σⅢ)， 带入式(22)可计算出每个应力状态的p、q、θ，利用这三个参数，生成线性方程组A×x=B见式(24)。

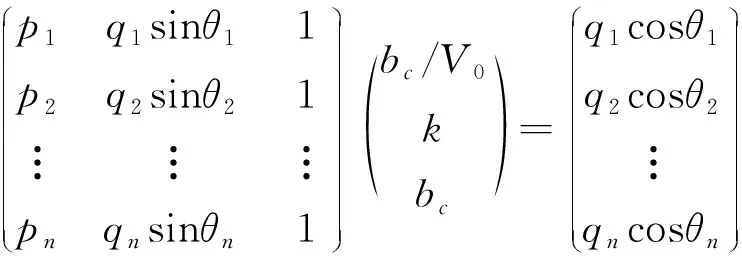
(24)

式中：A为矩形数据矩阵；x为参数向量；B为数据向量。

采用最小二乘法求解方程式(24)，获得bc/V0、k和bc。根据p-q平面中的轴对称压缩和延长线的表达式，求得φc和φe见式(25)。

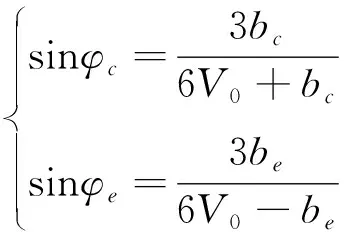
(25)

在p-q平面中，PMC准则用两个内摩擦角和顶点V0表示，可以写为式(26)。

(26)

式中：q为广义剪应力；p为平均应力；θ为应力洛德角(以最大主应力所在轴为0°)；φc为三轴压缩状态下的内摩擦角；φe为三轴伸长状态下的内摩擦角；V0为三向等拉状态下的假设强度；n为破坏机制组别(只有剪切破坏时n=1，考虑拉伸-剪切过渡段时n=2，同时考虑低压条件下最大线应变-过渡段-剪切应变时n=3)。

3 多重破坏机制强度的PMC模型试验研究

3.1 试验条件

以四川黄砂岩和金川二矿区深部花岗岩为试验对象，采用朝阳TAW-2000微机控制电液伺服岩石三轴试验机(图6)和北京科技大学地应力测量实验室自主研发的便携式自密封岩石三轴试验高压舱加压系统(图6)进行高压三轴压缩试验。

图6 试验加载设备Fig.6 Test loading equipment

花岗岩与砂岩试样制备参考《水利水电工程岩石试验规程》(SL 264—2020)中的相关规定，制备获得Φ30 mm×60 mm的标准岩石力学试件(图7)。

图7 制备的岩样Fig.7 Prepared rock sample

本文中常规三轴试验依赖两个独立的加载系统，因此不能利用系统设置来进行轴压与围压的同时同速率加载。为保证准静态条件，减小试验误差，采用轴压、围压分别独立的阶梯加载方式，阶梯加载见表1。试验过程中轴向加载过程中先采用应力控制，加载速率为100 N/s，当加载到静水压力状态后保持径向压力在试验过程中不变，然后以相同加载速率轴向加载至峰值强度的50%左右切换为变形控制，加载速率为0.03 mm/min。试验中围压加载过程中先采用粗控制，加载速率为1 MPa/s，当加载到静水压力状态前5 MPa后，采用微调控制手轮进行精控制，加载速率为0.2 MPa/s。

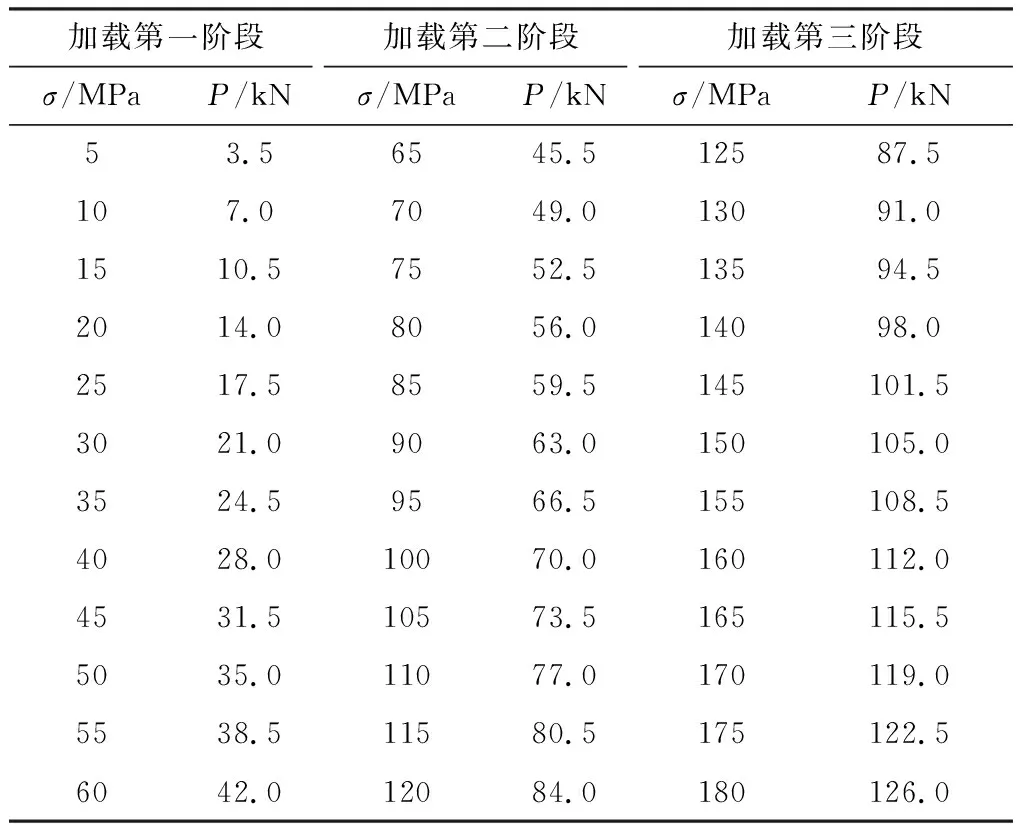
表1 阶梯加载轴向荷载与轴向应力对照Table 1 Comparison of axial load and axial stress under step loading

3.2 试验结果

通过上述阶梯式加载的试验方案对四川黄砂岩和金川花岗岩进行高围压常规三轴试验，其中，四川砂岩三轴压缩试验在0～170 MPa之间设置了16组不同的围压，金川花岗岩三轴压缩试验在0～160 MPa设置了13组不同围压。试验过程中典型的应力-应变曲线如图8所示(以部分花岗岩数据为例)，试验获得砂岩和花岗岩峰值强度随围压的变化曲线如图9所示，试样破坏形态如图10和图11所示。 由图8～图11可以看出，四川黄砂岩与金川花岗岩随着围压增加，其破坏模式表现出相似的规律：在低围压状态下破坏时，以剪切破坏为主，破坏面角度随着围压的增大而呈现减小的趋势；在较高围压时，角度依然在变小，慢慢呈现压剪破坏的趋势。

图8 常规三轴压缩试验曲线Fig.8 Conventional triaxial compression test curve

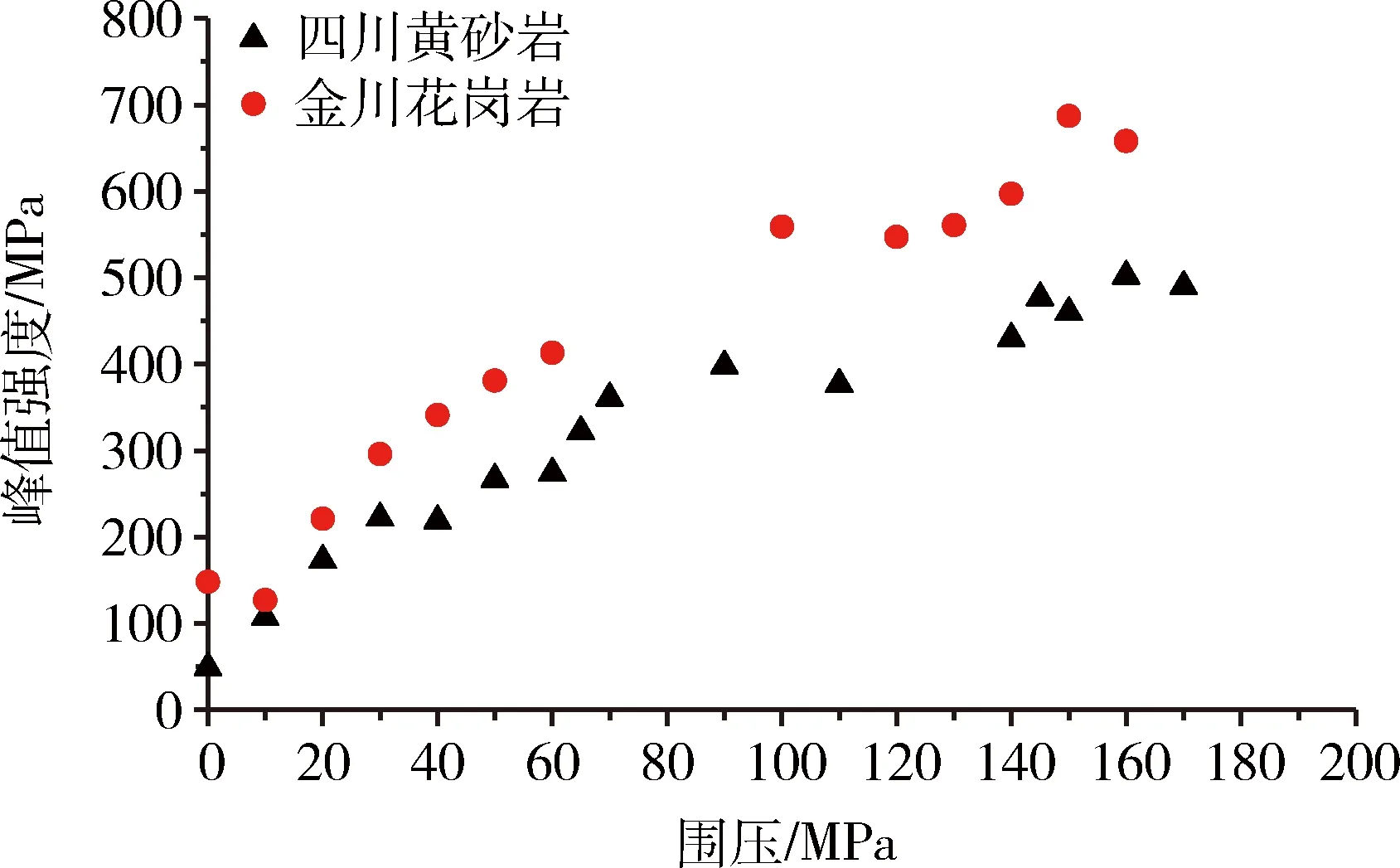
图9 常规三轴压缩试验结果Fig.9 Results of conventional triaxial compression test

图10 四川黄砂岩破坏形态Fig.10 Failure modes of Sichuan yellow sandstone

图11 金川花岗岩破坏形态Fig.11 Failure modes of Jinchuan granite

3.3 多重破坏机制强度的PMC模型适用性验证

1)n=1时(仅考虑剪应力控制段)。以Berea砂岩实验数据进行分析，实验数据见表2。图12为p-q平面中拟合破坏面和实验数据(常规三轴压缩实验和常规三轴伸长实验)的对比图。q的负轴表示三轴伸长实验，q的正轴表示三轴压缩实验，PMC准则拟合结果与实验结果吻合度较高，且常规三轴压缩实验的摩擦角小于常规三轴伸长实验的摩擦角。φc和φe的差异可说明中间主应力的影响。

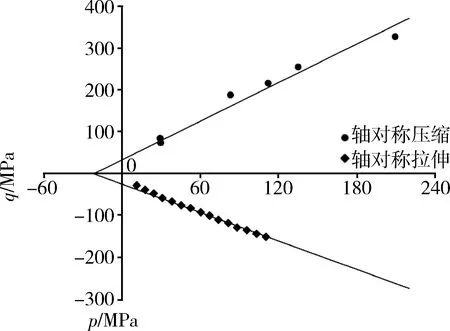
图12 Berea砂岩实验数据对比Fig.12 Comparison of experimental data of Berea sandstone

表2 PMC模型拟合结果数据Table 2 PMC model fitting result data

2)n=2时(考虑拉伸-剪切过渡段和剪应力控制段)。对金川花岗岩试样实验数据进行分析，为了保证V0(1)≥V0(2)，选择p≥200 MPa为第一段区域，p≤200 MPa为第二段区域进行六参数的PMC模型拟合，拟合结果见表3。图13为p-q平面中花岗岩六参数PMC模型，由图13可以看出， 花岗岩强度表现出了明显的分段线性特征，该特征可通过六参数PMC模型进行拟合。然而，由于缺少三轴拉伸试验数据，该模型仅适用于岩石拉伸剪切的过渡阶段，无法对花岗岩拉伸破坏模式进行表征。

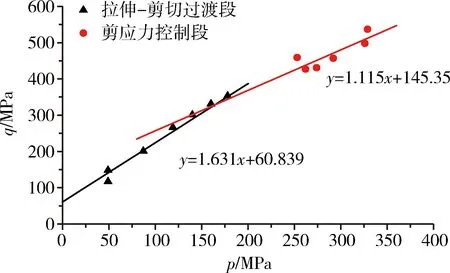
图13 花岗岩在p-q平面上的六参数PMC模型Fig.13 Six parameters PMC model of granite on p-q plane

表3 金川花岗岩PMC模型的六个参数Table 3 Six parameters of Jinchuan granite PMC model

3)n=3时(考虑线应变控制段-过渡段-剪应力控制段)。对四川黄砂岩试样实验数据进行分析，拟合结果见表4。图14为p-q平面中PMC拟合破坏面和实验数据对比图。由图14可以看出，黄砂岩强度表现出了较为明显的分段强度特征，此特征符合多重破坏机制影响下强度规律。

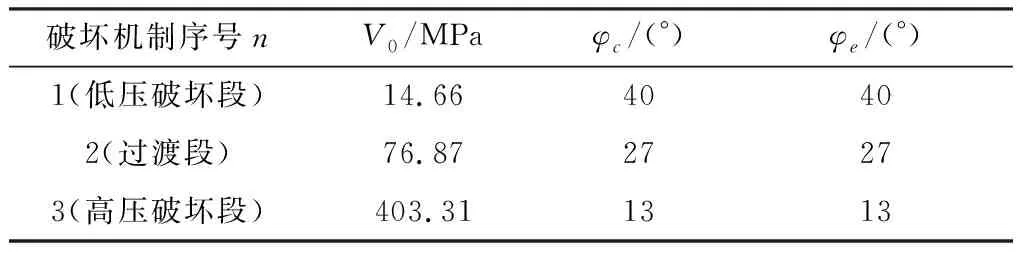
表4 砂岩多破坏机制影响下强度参数Table 4 Strength parameters of sandstone under the influence of multiple failure mechanisms

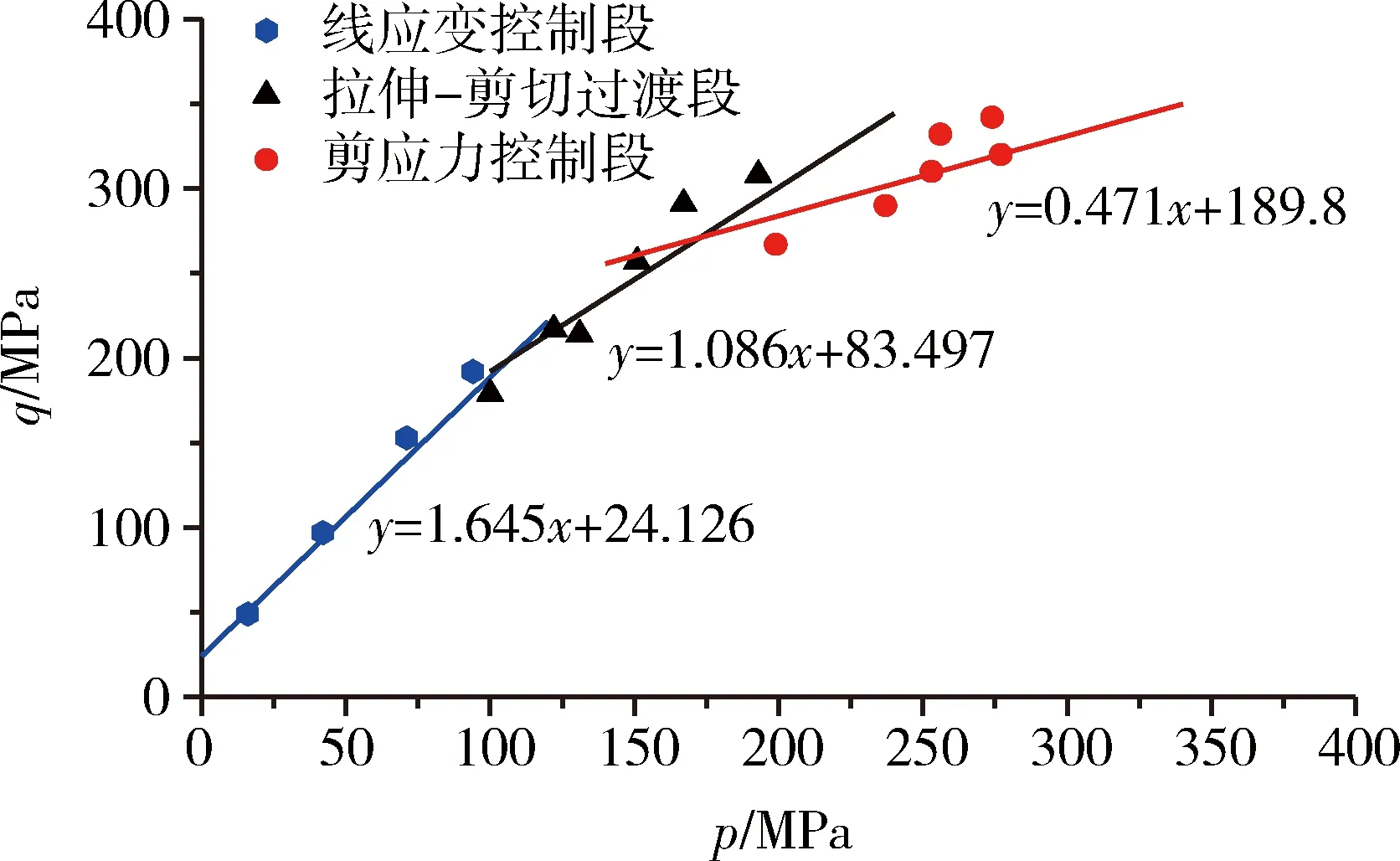
图14 黄砂岩强度多重机制破坏强度拟合Fig.14 Fitting of failure strength of yellow sandstone with multiple mechanisms

4 结 论

1) 基于PMC模型基本原则和最大线应变理论，提出了考虑包含最大线应变、最大剪应力破坏机制的分段线性强度准则。该强度准则考虑线应变控制段-过渡段-剪应力控制段三阶段强度，每阶段由控制性强度线决定强度大小。

2) 为统一表征单独破坏机制、双重破坏机制、多重破坏机制影响下强度过渡特征和数学表达方式，基于PMC基本强度参数与π平面应力关系，考虑强度准则在应力空间适用性要求，提出了广义剪应力、平均应力及应力洛德角为参量的的多破坏机制影响下强度准则的不等式统一形式。Mohr-Coulomb准则、PMC准则、十二边形PMC准则均为其特例。

3) 通过Berea砂岩、金川花岗岩和四川黄砂岩试验数据，分别对多重破坏机制PMC强度模型n=1(仅考虑剪应力控制段)，n=2(考虑拉伸-剪切过渡段和剪应力控制段)和n=3(考虑线应变控制段-过渡段-剪应力控制段)的情况进行拟合。 结果表明，岩石强度表现出了较为明显的分段强度特征，符合多重破坏机制影响下强度规律，从而验证了多重破坏机制PMC强度模型对于岩石材料的适用性。