雪雕模型的离散处理及基本单元位置优化
2022-11-21李建永董绪斌李来春王立才王开宝徐威震王昊天郭庆东
李建永,董绪斌,李来春,王立才,王开宝,徐威震,王昊天,郭庆东
(1.北华大学机械工程学院,吉林 吉林 132021;2.北华大学计算机科学技术学院,吉林 吉林 132021)
当前,雪雕产业快速发展,雪雕的需求量与日俱增,传统的制作方法已不能满足冰雪旅游产业的需求,雪雕制作的机械化和智能化成为主要的发展趋势,而利用操作难度低、效率高的智能化3D雪雕打印设备制作雪雕[1]取代传统的制作工艺,可以提高制作效率,能够适应雪雕行业快速发展的需要.由于加工的高效性和灵活性,3D打印越来越多地被应用到不同领域[2-7].智能化3D雪雕打印设备基于增材制造技术理念,以雪砖为基本单元,以传统工程车辆为载体,在其上安装一个关节机器人作为执行单元.施工时,将提前预制好的雪砖依照雪雕的三维模型,通过执行单元逐一摆放至指定坐标位置,逐层叠放,实现大型雪雕的快速制作.雪砖逐层叠放形成雪雕是一个填充问题[8],属于在规定约束下的空间填充,可分为规则填充和不规则填充两类.对于前者,HALES[9]在1998年完成了Kepler猜想的证明;对于不规则填充,由于随机填充与物质结构关系密切而被广泛研究,并取得了很多成果[10].近年来,关于填充问题的研究形成了3个主要方向,分别是自由装填、覆盖填充和填充,它们之间既有区别又有联系,但追求的目标一致,即研究获得最大填充率的填充方法[11].显而易见,对颗粒堆积填充问题的研究具有理论意义和应用价值[12].
在智能化3D雪雕打印设备逐层构建雪雕时,打印系统的操作单元依据该层所在高度雪雕模型截面的二维轮廓摆放雪砖,因此,确定轮廓边缘雪砖的坐标信息尤为重要,这些坐标信息通过对雪雕模型进行数字化处理获得;同时,雪砖摆放的具体位置决定雪雕与原模型的近似程度.本文探讨雪雕三维模型的等高分层处理方法,将雪雕的三维模型转化为二维轮廓,为雪雕3D打印的实施提供理论依据;讨论雪砖在某一切面的位置优化策略,以达到最大填充率,进而获得最优复现雪雕三维模型;通过模拟试验,验证雪砖摆放策略的可行性及有效性.
1 雪雕模型的离散处理
通过MATLAB实现对STL格式雪雕模型文件的数字化离散处理,主要包括模型切分和坐标点提取.等高分层算法实现对模型的切分,获取二维轮廓信息;获得轮廓内雪砖中心点的坐标信息,雪砖按此坐标摆放,完成对二维轮廓的填充.
1.1 等高分层原理
由于实体雪雕是通过逐层累积完成的,因此,求出雪雕模型在每一层的边界轮廓曲线至关重要.
模型的分层处理是指通过一系列相互平行的水平面(即切分平面)与模型相交,求得相交后的轮廓曲线.雪雕STL模型通过三角面片形式组成物体的三维形状,对模型进行切分就是求出切分平面和与其相交的三角面片的交线,交线相互连接即得到一定高度下模型的轮廓线.
智能化3D雪雕打印是以一定尺寸的雪砖为基本单元来填充轮廓,因此,其切分平面间距为等距,属于等高分层[13-15].等高分层的算法思想是在固定的距离进行一次模型切片处理[16],通过求解其交线获得模型的轮廓线.模型切分流程见图1.
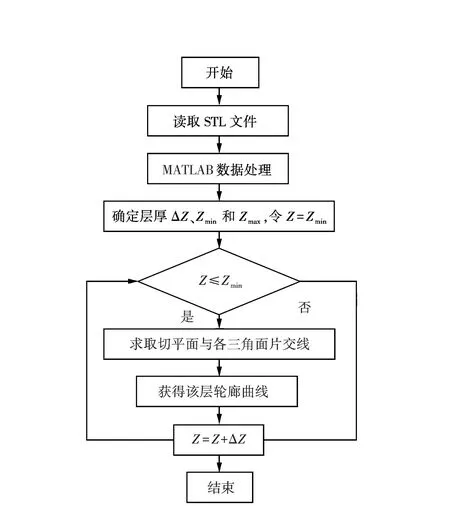
图1模型切分流程Fig.1Model cutting process
1.2 雪雕模型截面轮廓获取
通过计算某一分层高度下切平面和与其相交的三角形面片的交线获得该分层高度下模型的轮廓线.图2为切平面与某三角面片交线的示意图.
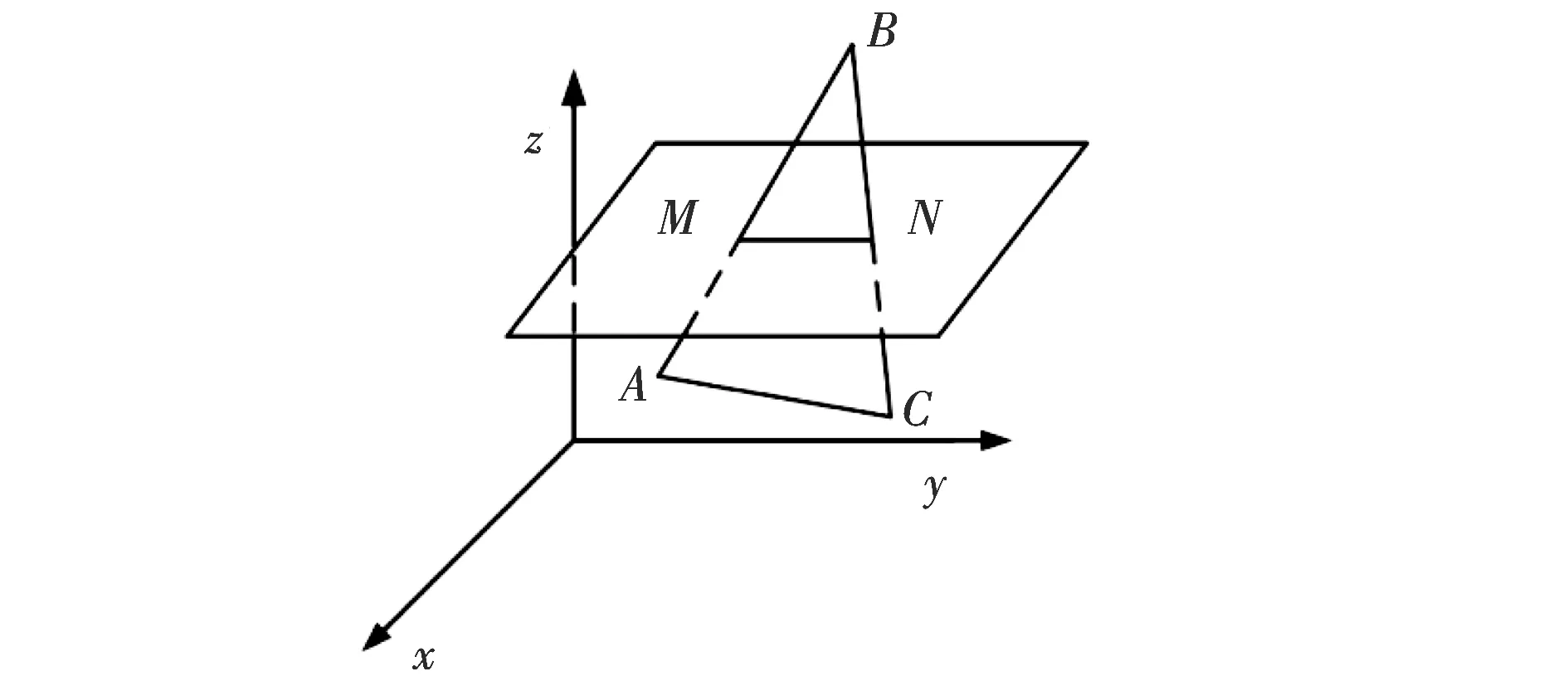
图2三角形面片与切平面相交Fig.2The triangular face piece intersects with the cutting plane
已知点A、B、C的空间坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),设M点坐标为(xm,ym,z0),N点坐标为(xn,yn,z0).通过空间直线参数方程可得M点坐标为
(1)
N点坐标为
(2)
通过式(1)、(2)可得到特定高度下切平面和所有与其相交三角面片的交线,即可获得该切分高度下模型的轮廓曲线.
1.3 等高分层切片试验
根据等高分层算法,使用MATLAB平台编程求解,对三维模型进行切片试验.将模型导入MATLAB并读取数据信息,显示所获取的三角面片.将STL模型文件按照z轴方向进行切分,切分高度可以设置为模型高度范围内的任意值.轮廓化算法实现:
第1步,读取每个STL文件的三角面片信息,从而得到每个三角形面片的顶点坐标与法向量,以及模型所含的三角形数量N,其中,n是N个三角形中的第n个.
第2步,通过读取模型STL文件得到的每个三角形面片顶点坐标,求出模型z方向的最小值Zmin与最大值Zmax.
第3步,由人为给定的切片分层高度ΔZ和Zmin、Zmax得到切片高度向量Z=[Zmin+ΔZ,…,Zmin+kΔZ,…,Zmax-ΔZ]T.其中,Zmax-ΔZ=Zmin+KΔZ,K为该模型切片层数,k为K层切片中的第k个.
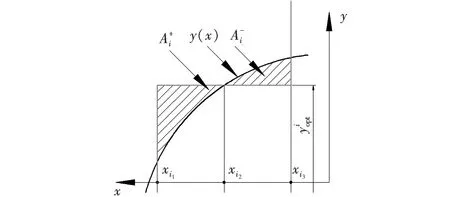
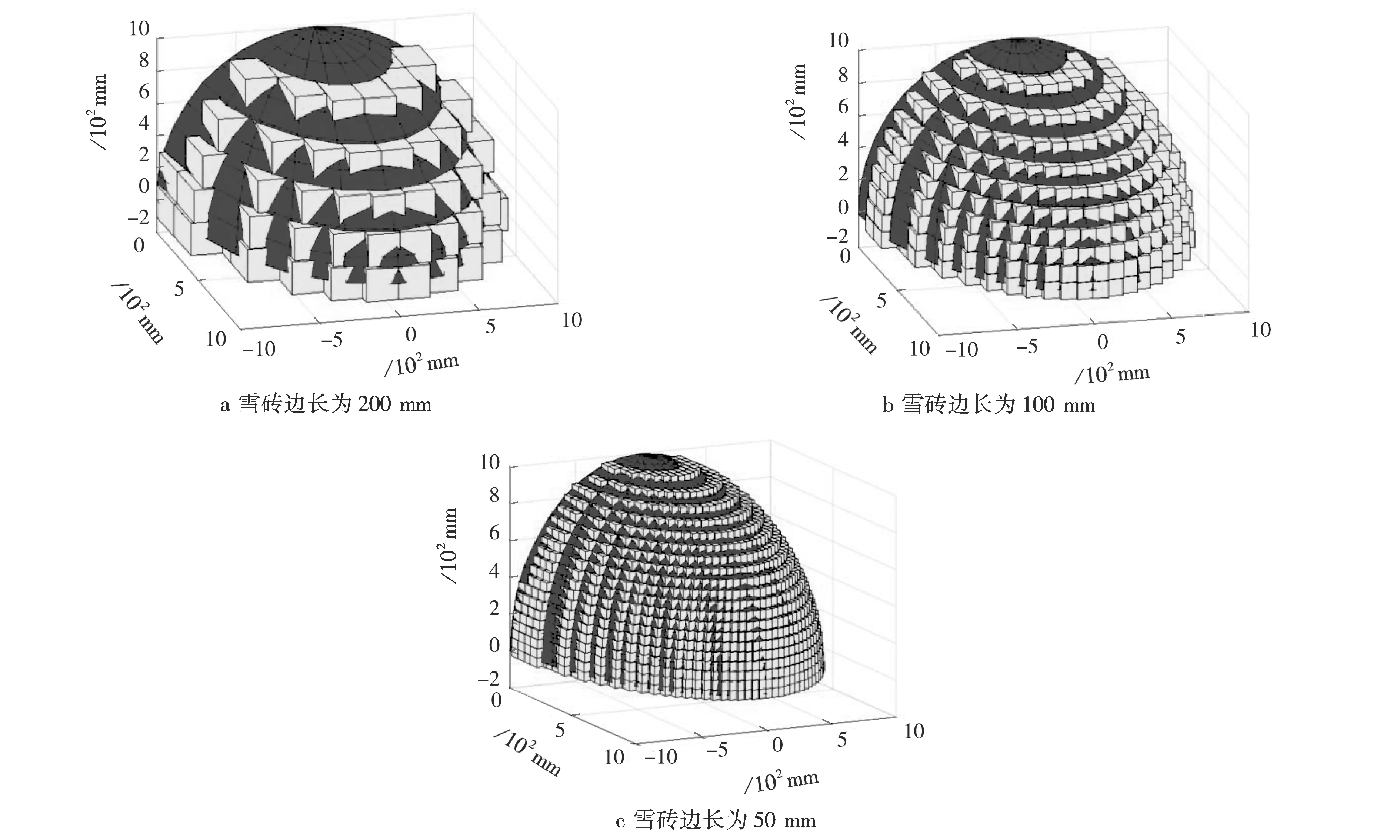
第4步,逐层求得切平面与各三角形面片的交点,计算到第k层时Z0=Z(k),遍历每一个三角面片,如果该三角形z方向的最小值Zmin与最大值Zmax满足Zmin 图3球体模型切分结果Fig.3The results of the cut of sphere model 图4小黄鸭模型切分结果Fig.4The result of the cut of little yellow duck model 通过球体和小鸭子的三维模型切分试验分析可知,该算法实现了对模型的切分,且可以根据需要设定分层高度,获得雪雕模型各个高度切面所需的二维轮廓. 3D雪雕打印系统将雪砖逐层叠放制成雪雕,雪砖堆积后形成的整体轮廓即为雪雕外形,其过程借鉴了有限元思想,将模型离散后再装配成整体.雪雕的外形与模型相似度越高,雪雕就越逼真.显然,相似度与雪砖的尺寸有关,尺寸越小,相似度越高;圆柱体的雪砖要比立方体的雪砖能更好地逼近复杂轮廓,但考虑到工程实际,立方体雪砖是最好的选择,容易制备也易摆放,且稳定性好.本节主要探讨立方体雪砖的摆放策略,以使雪雕与模型的相似程度更高,获得最优摆放策略. 每一层雪砖摆放依据的是雪雕模型在该高度下的二维轮廓,并用雪砖填充该区域.前文提及的覆盖方法是一种可覆盖边界的填充,填充对象之间可以相互重叠且与区域界也可以重叠,最后将目标区域全部覆盖,见图5 a;用立方体雪砖填充雪雕二维轮廓所围成的区域,其所形成的边界就构成雪雕轮廓,由图5 b覆盖后的轮廓可以看出,填充效果与雪雕原轮廓相比并不理想,原因是该覆盖法需完全覆盖二维轮廓,导致覆盖后的轮廓与雪雕原轮廓误差较大.为了提高雪雕与模型的相似度,应减少误差,使二者轮廓尽可能接近. 图5覆盖填充Fig.5Covering fill图6改进覆盖Fig.6Improved covering fill 图6为另外一种雪砖填充策略,与覆盖法相比,最大区别是它不追求覆盖边界,而是使在轮廓边缘处的雪砖凸出和凹进轮廓的面积很小,减少了误差,提高了相似程度. 依据以上所述,相似度为在雪雕的某一切面中所有的凸出和凹进轮廓的误差面积A,即 (3) 综上所述,在构建雪雕过程中,如果要求雪雕与原模型逼近,就要使相似度高(即误差面积A小).显然,受到一些条件约束,误差面积A不可能无限减小,受雪砖单元的制备成本及实际使用要求限制.比如,尺寸越大,雪雕制备的效率越高,但相似度不容易保证;尺寸越小,相似度越好,但效率低,且不易被执行单元夹持.因此,雪砖的具体尺寸应根据雪雕大小、工作效率等多实际工况确定. 在雪砖尺寸确定后,摆放位置对相似度起决定作用.这时,使相似度达到最大(误差面积A最小)的问题可被归结为规划问题,问题的目标函数为误差面积A,约束条件是雪砖之间的位置关系.数学规划模型可表示为优化问题(P),即 (4) 式中:xi、xj(i,j=1,2,…,n)为雪砖中心点在x-y平面内的坐标;a为立方体雪砖的边长;n为与二维轮廓相交的雪砖数量. 图7误差面积Fig.7Error area 由图6可知,目标函数误差面积A的变量是雪砖中心点坐标(xi,yi,zi),当层高固定时(即z固定),变量就仅为x和y了,但x坐标受式(4)中约束条件的限制,因此,误差面积A仅是y坐标的函数(图7): (5) 综上,优化问题P可归结为在x坐标及立方体雪砖边长的约束下获得使误差面积A最小的雪砖中心点yi(i=1,2,…,n)的坐标. 根据优化问题P,使用MATLAB平台进行编程求解各层雪砖中心点最优位置.通过之前的轮廓提取算法可以得到每层轮廓的点坐标,从而得到该层x方向坐标最小值xmin和最大值xmax,根据式(4)中的约束条件可以得到该层x方向最优点坐标向量 以及该层轮廓最优点个数M,其中,xmax-L/2=xmin+(2m-1)L/2,m为该层轮廓中第m个最优点.所以,问题转化为求出该层y方向最优点坐标向量.对于第m个最优点的y方向坐标Yopt(m),首先进行随机初始化使 ymin 然后搜索该层上属于xmin+(m-1)L≤x≤xmin+mL的点,将式(5)中的面积表达式进行离散化处理,表示为 其中:K+为此时该层轮廓等间隔插值后小于此时Yopt(m)的y方向坐标点;K-为此时该层轮廓等间隔插值后大于此时Yopt(m)的y方向坐标点,然后代入式(4),运用二分法迭代查找出最优解Yopt(m). 为验证上述优化算法,对球体进行切分及雪砖堆积模拟试验,获得模型边界处雪砖中心的最优位置.模型中,球体的半径设置为1 000 mm,使用的立方体边长a=100 mm.球体模拟堆积见图8.其中,图8 a为按覆盖方法填充球体,图8 b为优化yi(i=1,2,…,n)坐标后填充球体.对比可以看出,雪砖依据最优坐标点堆积搭建球体,很好地拟合了原模型.由此说明,雪雕模型数据处理可行且有效,可为后续进行智能化3D雪雕打印设备理论分析及采用雪砖进行模型搭建提供参考. 图8球体模拟堆积Fig.8Sphere simulation stacking 图9不同尺寸雪砖模拟堆积Fig.9Simulated accumulation of snow bricks of different sizes 机器人模型搭建通过库卡机器人试验平台进行物体抓取及摆放试验.试验中的长方体为木质材料,规格为50mm×25mm×20mm.在库卡机器人控制部分,通过离线编程将优化算法生成的坐标点编入机器人控制程序中,实现机器人自动进行模型的搭建.机器人搭建效果见图10. 图10机器人搭建效果Fig.10Construction effect of robot 使用机器人依次摆放木制长方体完成小鸭子模型打印.该试验实现了机器人对木质长方体的抓取以及将其摆放到小鸭子模型的各个最优坐标点,完成模型搭建,整个模型的搭建效果较好. 本文研究了三维模型等高分层和雪砖位置优化.对三维雪雕模型进行数字离散处理,转化为二维轮廓,以此为雪雕3D打印提供理论依据;进行雪砖堆积位置优化,以达到最大填充率,实现最大程度复现原模型;利用MATLAB实现对STL格式的模型文件的数字化处理,用等高切分算法实现模型的切分及优化算法,提取雪砖坐标点;通过仿真及机器人完成小鸭子模型打印,验证了模型处理和位置优化方法的可行性及有效性. 本文在研究三维模型的等高分层和雪砖位置优化时,默认的雪砖为立方体,且尺寸一致.显而易见,雪雕各部位复杂程度不一,形状复杂的部位采用尺寸小的雪砖堆积,会使雪雕更逼近原模型,且不同形状的雪砖会使雪雕获得不同的效果,在以后的研究中,需在这方面进行探讨.


2 雪砖填充优化策略
2.1 相似度的基本概念


2.2 雪砖摆放位置优化
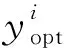
2.3 雪砖摆放位置优化及模拟试验验证


3 小黄鸭雪雕模拟验证

4 小 结
