基于混合特征的复合多核SVM变压器故障诊断

曲丽萍，周浩涵，刘冲杰，高泰路，何昌龙，崔文超，刘 斌

通常，在不同故障状态下，变压器油和绝缘体会产生不同含量的特征气体，如氧气(O2)、氮气(N2)、氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)、一氧化碳(CO)、二氧化碳(CO2).变压器故障诊断常采用溶解气体分析(DGA，Dissolved Gas Analysis)技术，即基于油中溶解气体组分与变压器故障类型之间的对应关系，判断变压器内部有无异常情况，诊断故障类型、故障方位、严重程度和发展趋势.DGA变压器故障诊断可分为特征气体法[1]、IEC三比值法[2]、四比值法[3]、图形法[4]等，这些算法虽然都取得了一定成效，但由于特征气体含量与故障类型之间诊断模型的模糊性和不确定性，导致诊断效果常常不尽人意.支持向量机(SVM，Support Vector Machine)作为机器学习方法，已被引入到变压器故障诊断领域，其基本原理是通过训练集数据的算法计算，建立故障特征气体输入与故障诊断类型输出的训练模型，实现变压器潜在故障诊断.但支持向量机的模型参数难以确定、可操作性复杂，诊断效果常常不够理想.因此，人们开始研究参数寻优算法，如模拟退火算法[6]、遗传算法[7]、粒子群算法[8]、应用多分类多核学习[9]、布谷鸟算法[10]、模糊算法[11]等，希望通过在最优分类面附近搜索，寻找到最佳参数，获得更精确、更逼近的分类结果.

本文针对DGA气体分析特点，开展油浸式变压器故障诊断研究，通过改进支持向量机模型不足，实现更有成效的电力变压器故障诊断.首先，拓展特征量范围，全方位、多角度地挖掘故障特征气体与故障类型之间的映射关系.在通常的SVM模型5种特征气体特征量的基础上，增补DGA技术的特征气体含量三比值，将特征气体含量的绝对关系与特征气体比值的相对关系互补相加，共同作为SVM的输入特征量，最大限度地涵盖客观映射关系的表征内容.其次，为解决SVM模型中单核核函数在复杂工况下针对性不足的问题，构建加权复合多核核函数的SVM模型，利用合成原理改进原始数据变换后的新空间，同时采用差分进化算法优化支持向量机的相关参数.

1 支持向量机模型

1.1 线性分划

支持向量机是在统计学理论基础上发展起来的机器学习方法，在解决小样本、高维数和非线性等问题方面具有很多优势[5].支持向量机基础算法属于线性二分类方法，即构造一个超平面，将如图1所示的平面划分归为两个类别部分，图中圆圈和三角形分别代表不同类别.

图1线性二分类Fig.1Linear binary classification

对于图1的分类问题，考虑选择合适的直线(w，x)+b=0，将两个类别点划分开，其中，(w，x)是w=(w1，w2)T和x=([x]1，[x]2)T的内积，直线两侧点分别对应y为类别1和-1，进而按照式(1)推断新点x对应的类别y：

y=f(x)=sgn(g(x))=sgn((w，x)+b)，

(1)

其中：sgn(·) 是式(2)定义的符号函数，

(2)

当g(x) 为线性函数g(x)=(w，x)+b时，决策函数f(x)对应：使用超平面(w，x)+b=0将n空间分成两部分，称为线性分类机；当g(x)为非线性函数时，决策函数f(x)对应：使用曲面将n空间分成两部分，此时称为非线性分类机.

(3)

(4)

(5)

s.t.yi((w，xi)+b)≥1，i=1，2，…，l.

(6)

为获得式(5)、(6)的对偶问题，引入Lagrange函数

其中：α=(α1，α2，…，αl)T为Lagrange乘子向量.

定理1最优化问题

(7)

(8)

αi≥0，i=1，2，…，l

(9)

是原始问题式(5)、(6)的对偶问题.

对偶问题(7)～(9)的最大化问题可以等价采用具有相同解集的(10)～(12)的最小化问题来求解：

(10)

(11)

αi≥0，i=1，2，…，l.

(12)

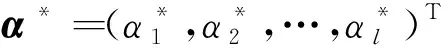
f(x)=sgn(g(x))，

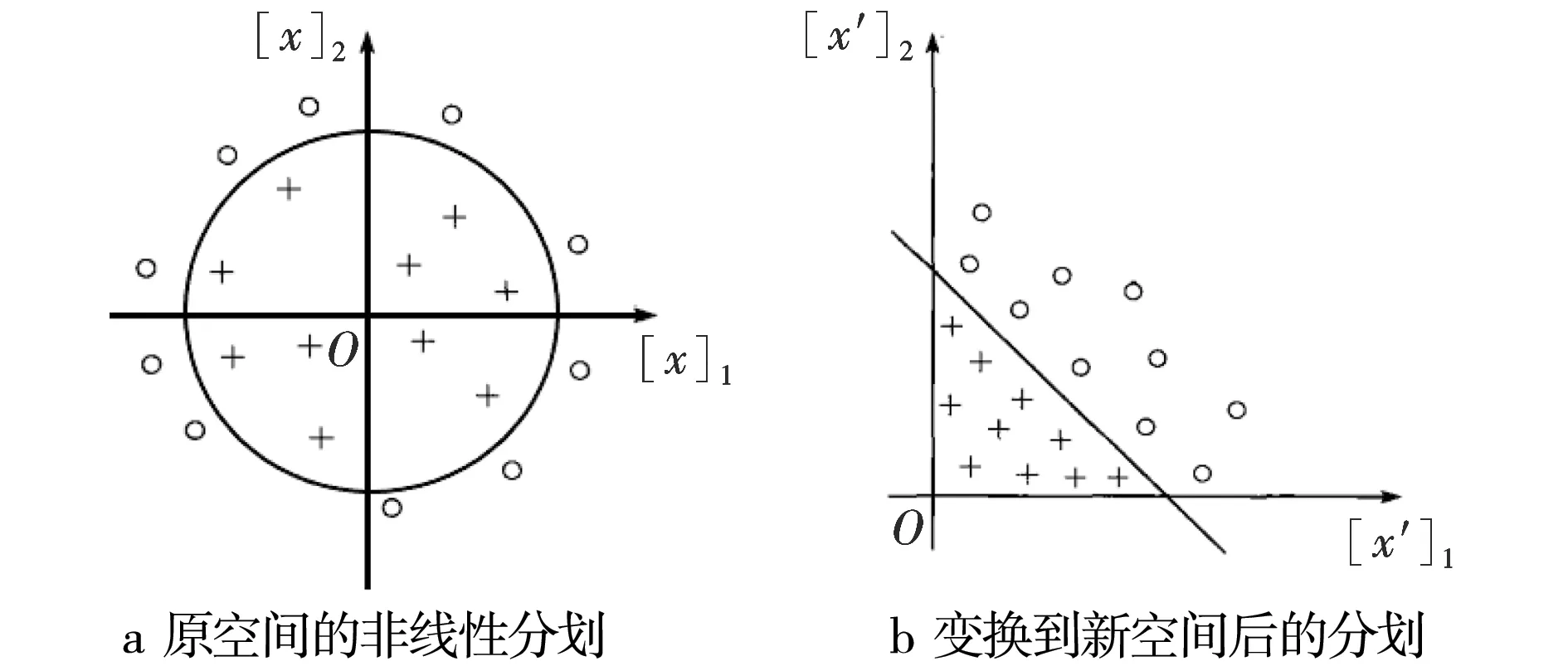
图2非线性分划Fig.2Nonlinear classification

1.2 非线性分划

某些分类问题见图2.要将图中“+”和“°”两类点分划开，合理的分划线应该是 ([x]1，[x]2)平面上以原点为中心的圆，这就是非线性分划.考虑从 ([x]1，[x]2)平面上的点x=([x]1，[x]2)T到 ([x]1，[x]2)平面上的点x=([x]1，[x]2)T的变换xΦ=Φ(x).

只要使用变换xΦ=Φ(x)将原平面上的点变换到新平面上，在新平面上使用线性支持向量机求出分划直线，将新平面上的分划直线再变换回到原平面，就可以得到实现非线性分划的分划曲线和决策函数.

因此，得到基于非线性分划的分类算法：

设训练集为

T={(xi，yi)，i=1，2，…，l}∈(n×Y)l，

其中：xi∈n；yi∈Y={-1，1}，i=1，2，…，l，引进从空间n到Hilbert空间H的变换xΦ=Φ(x)，见式(13)：

Φ：n→H，x→xΦ=Φ(x).

(13)

训练集T经式(13)变换为

TΦ={(xi，yi)，i=1，2，…，l}∈(H×Y)l，

其中：xΦi=Φ(xi)∈H；yi∈Y={1，-1}，i=1，2，…，l，然后需要求出此空间H中线性分划超平面(w*，x)+b*=0，从而导出在原空间n上的分划超平面(w*，Φ(x))+b*=0)和决策函数f(x)=sgn((w*，x)+b*)=sgn((w*，Φ(x))+b*).

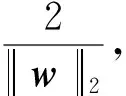
(14)

s.t.yi((w，Φ(xi))+b)≥1-ξi，i=1，2，…，l，

(15)

ξi≥0，i=1，2，…，l，

(16)

其中：C和ξi为惩罚因子和松弛变量.当ξi充分大时，约束条件式(15)总会满足.为避免ξi取过大的值，引入惩罚因子C.

引进Lagrange函数

其中：α=(α1，α2，…，αl)T和β=(β1，β2，…，βl)T为Lagrange乘子向量.

按照前面线性分划的求解方法，通过求解非线性分划原始问题(14)～(16)的对偶问题，可获得非线性分划的解w*和b*，见式(17)、(18)：

(17)

(18)

构造决策函数，见式(19)、(20)：

f(x)=sgn(g(x))，

(19)

(20)

利用核函数代替式(20)中的特征空间内积，得到最优分类函数，见式(21)：

(21)

其中：K(xi，x)为满足mercer核定理的核函数.

上述过程为支持向量机的线性二分类过程，而变压器故障诊断是一个非线性分类的过程，支持向量机通过引入核函数解决非线性分类问题[5].

2 电力变压器的DGA故障诊断原理

大容量变压器通常为油浸式的，油箱中的油起绝缘和冷却作用.长期运行的变压器在热和电的作用下，会引起变压器中油、绝缘纸中有机化合物分解，产生的不同烃类气体最终会溶解在变压器油中.针对变压器油进行检测，分析和诊断变压器潜在的故障类型，被称为溶解气体分析技术(DGA).DGA实质是分析油中特征气体含量，按照规定的比值规则表，找到与之对应的状态类型[2，4].

变压器运行过程中产生的特征气体包括H2、CH4、C2H6、C2H4、C2H2、CO、CO2.在变压器故障诊断中，常将前5种气体含量纳入模型数据.基于DGA气体分析技术的诊断模型见图3.通过原始留存数据，利用智能算法进行模型训练，得到状态类型预测模型，当需要分析、评估某一定量数据时，采用此模型识别变压器状态类型，评估目前故障程度，确定变压器的维护措施.

图3基于DGA分析技术的变压器状态预测模型Fig.3Prediction model of transformer state based on DGA technology

3 混合型复合多核支持向量机变压器故障诊断模型

3.1 混合型特征输入量构建

以往的变压器支持向量机诊断模型，或者是采用5种特征气体含量作为输入特征量，忽略各种特征气体含量间相对关系，造成分类准确率不高；或者是利用特征气体含量的3个比值作为特征输入，没有全面考虑各气体含量的绝对值大小，诊断效果不够理想.

考察大量变压器故障诊断结果发现，变压器故障诊断不仅需要综合考虑油中溶解气体各组分的绝对含量信息，还需要详细考虑各组分之间的相对含量.特征气体的绝对含量信息体现的是变压器故障状态的程度，将直接影响特征量在特征空间中的位置；而特征气体的相对含量则反映变压器故障状态的性质，对各特征量在特征空间中的相对位置有着重要影响.要获得精准诊断结果，就要构建出能够最大程度表征映射规律的特征量.本文希望通过构建特征气体含量的绝对与相对信息的混合型特征量，寻找到突破支持向量机模式识别瓶颈的新途径.

混合型特征量是从绝对和相对的角度吸纳数据构建特征量，特征量训练数据本身就在一定程度上涵盖了溶解气体含量与变压器状态之间的客观映射规律，这样训练出来的诊断模型才能更好地挖掘出数据内部包含的映射关系，才会更大程度地体现变压器自身的映射规律，采用这样训练构建的诊断模型才能更为客观地获得新数据对应的诊断结果.

本文构建SVM变压器故障诊断模型的混合型特征输入量包括变压器5种特征气体含量：氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)；5种特征气体含量之间的3个比值：x1=C2H2/C2H4，x2=CH4/H2，x3=C2H4/C2H6.

3.2 复合多核支持向量机的变压器诊断模型

在利用支持向量机解决非线性分类问题时，核函数的作用是代替内积，实现更为简单地将原始数据变换到新的空间.选择使用不同的核函数，变换到新空间的结果不同，最终的分类效果也会不同.常见的核函数如下.

1)线性核函数：K(x，y)=(x，y)，实际上就是原输入空间中的点积.

2)多项式核函数：K(x，y)=((x，y)+p)q，p≥0，其中：q为任意正整数.多项式核不仅对样本附近点起作用，对远离样本点也起作用，称为全局核函数，泛化能力强，善于提取样本的全局信息.

4) Sigmoid核函数：K(x，y)=tanh(γ(x，y)+c).Sigmoid广泛应用于支持向量机，是一种全局核函数.

基于上述核函数特点，本文核函数的构建采用两种策略：一是将上述4种核函数按照不同分类问题进行加权复合，形成不同分类问题的特型核函数，实现多特征空间的融合，获得更好的分类识别效果；二是通过参数优化来进一步增强SVM核函数的适应性，提升SVM模型的分类效果.

3.2.1 复合加权多核核函数的构建

变压器故障诊断属于非线性分划问题，而非线性分划又是通过将原始点变换到新空间，并在新空间中借助线性分划方法完成.选择合适的变换(即核函数)构建新空间，是基于支持向量机的变压器故障诊断实现精准分划的关键.

支持向量机有4种常见核函数，每种核函数在可分性、非线性、全局性、泛化能力等方面各具优势.将上述单核核函数不限类别地适当选择出若干进行加权整合成为复合多核核函数，采用这个复合多核核函数对非线性分划原始点进行空间变换，即相当于按照具体分类问题的实际情况，选择性、自适应地构建出与之匹配的新空间，而这个新空间在可分性、非线性、全局性、泛化能力方面将更加优越.

本文构建的加权复合多核核函数如式(22)：

(22)

其中：Ki(x，y)为SVM的第i类核函数；wi为SVM第i类核函数权重.构造决策函数如式(23)：

(23)

上述加权复合多核核函数实现的空间变换见图4.

图4复合加权多核核函数新空间构建Fig.4New space construction of composite weighted multi kernel of kernel function

最后，利用“一对一”的支持向量机多类型分类算法，得到加权复合多核核函数的支持向量机变压器多状态分类算法.

3.2.2 SVM核函数参数优化

在支持向量机的实际应用中发现，在缺乏对所研究样本数据先验知识的认识时，只要参数选择合适，采用非线性核函数总会取得不错的效果.在SVM中，体现分类最大化间隔和避免错分情况间折中概念的惩罚因子C的选择对SVM的分类效果也有着很大影响.故将非线性核函数g值、惩罚因子C及权值w统一纳入优化框架.

差分进化算法 (Differential Evolution Algorithm，DE) 是基于群体的启发式搜索算法，群中的每个个体对应一个解向量，与遗传算法类似，包括变异、交叉和选择操作，是一种高效全局优化算法.本文采用差分进化算法，实现g值、C值及权值w的优化，基本思想是从当前种群提取方向信息和搜索步长，为提高种群多样性增加随机差分和交叉，通过变异和交叉，生成新的临时种群.对当前种群和临时种群进行对比、选择，产生新一代种群，按此方法对种群不断进化，直至满足终止条件.

g值、C值及权值w的差分进化算法：

1)编码策略.采用实数编码策略，定义参数g和C的范围.

2)适应度函数的确定.在寻优过程中，适应度函数决定了进化的方向.本文适应度函数的构造基于交叉验证，将每一类故障数据的一部分用作训练，另外一部分用作测试，验证构造适应度函数值，每一类数据进行K次分组校验，最终确定适应度函数值.适应度具体计算过程：

① 将S个样本数据各自随机地分成K个相互独立的基本相等的子集；

② 将其中一部分作为训练集，另外一部分作为测试集，形成K个模型以及K个模型对应的正确率，且每个模型出现的概率情况p=1/K，K为S个样本的随机分组数；

③ 将K个模型期望E作为DE的适应度函数，如式(24)所示，用以评估待选择的参数g和C.

(24)

3)差分进化算法操作.

Step 1：初始种群的产生.对核函数参数g和惩罚参数C进行寻优，范围设定为(0，100)，利用MATLAB函数rand(1)，按照式(25)形成随机初始种群.

(25)

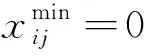
Step 2：种群变异操作.随机选择种群中的3个不同个体xp1、xp2、xp3，按照式(26)进行种群变异操作.

hij(t+1)=xp1 j(t)+F(xp2 j(t)-xp3 j(t))，

(26)

图5差分进化算法参数寻优流程Fig.5Parameter optimization process of differential evolution algorithm

其中：xp2 j(t)-xp3j(t)为差异化向量；F为缩放因子，本文F取 0.6；p1、p2、p3为随机数，表示个体的序列号.

Step 3：交叉操作.交叉操作是为了增加群体的多样性.设置基本参数交叉概率Rp∈[0，1]，Rp取0.7，交叉操作按照式(27)进行.

(27)

Step 4：选择操作.将Step 3交叉得到的个体向量vij(t+1)和目标向量xi(t)利用式(24)适应度函数进行比较、选择，选择操作按照式(28)进行.

(28)

Step 5：最优结果.逐代进化，判断终止条件，若未达到进化终止条件继续执行Step 2～Step 4 ；若达到终止条件，进化结束，获得最优进化个体g值和C值.

差分进化算法参数寻优实现流程见图5.

4 仿真试验与结果分析

4.1 仿真试验数据集

变压器运行环境不同，故障原因各不相同.本文搜集某变压器厂、发电厂及某省电科院220组不同电压等级、不同运行环境的变压器故障数据，见表1.

表1 实际变压器故障数据Tab.1 Failure data of actual transformer

4.2 仿真环境及分析方法

采用支持向量工具箱libsvm及MATLAB R2018b仿真软件进行分析.

分析检测采集到的故障油样，对其中5种气体含量进行整理、归类、编号，获得200组数据集.每种故障类型取15组作为训练集，10组作测试集.为减少数据间的差异，将数据按照式(29)作归一化处理.

(29)

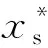
4.3 试验仿真结果与分析

为验证本文算法的有效性，以5种特征气体含量算法(简称5特征)、特征气体3比值算法(简称3特征)和混合型特征量输入及传统RBF核函数SCM算法、加权复合多核SVM算法、差分优化的混合特征加权复合多核SVM算法的故障诊断模型进行仿真对比，结果见图6～图11.仿真获得差分优化最佳参数：最佳惩罚因子C=53.737 6；复合多核核函数中的4个单核核函数的最佳参数g=[10.480 5，5.174 0，14.466 8，8.892 9]；4种核函数的最佳权值w=[0.606，0.004 2，0.340 5，0.049 2].

图63特征输入SVM算法仿真结果Fig.6Simulation results of 3 feature-input SVM algorithm图75特征输入SVM算法仿真结果Fig.7Simulation results of 5 feature-input SVM algorithm图8混合型特征输入SVM算法仿真结果Fig.8Simulation results of hybrid feature-input SVM algorithm图9差分优化的混合特征加权复合多核SVM算法仿真结果Fig.9Simulation results of hybrid feature weighted composite multi-kernel SVM algorithm

由图6～图8 可见，混合特征输入量SVM诊断模型的诊断正确率最优.图8、图9都是使用了混合特征量输入的仿真结果，但图8采用的是单核RBF核函数，且核函数参数未作优化；而图9采用的是加权复合多核核函数，且核函数参数g值、C值、权值w进行了差分优化.可以看出，图9的诊断准确率更加令人满意.

图10、图11分别是训练集、测试集的仿真结果，显示了使用5特征、3特征、混合特征量输入方法，传统RBF核函数、加权复合多核核函数及差分优化的加权复合多核核函数的SVM算法仿真结果.由图10、图11可见：无论训练集还是测试集，差分优化的加权复合多核核函数SVM算法的仿真结果更具优势.

图10训练集准确率Fig.10Training set accuracy图11测试集准确率Fig.11Test set accuracy

数据相同、SVM模型不同的变压器状态识别结果对比见表2.由表2可见：1)采用不同方法选取SVM模型特征量，获得的状态识别结果大不相同，无论采用训练集数据仿真，还是测试集数据仿真，本文构建的混合特征输入量方法的状态识别正确率都明显高于5特征输入量和3特征输入量方法；2)采用不同方法构建SVM模型核函数，得到的状态识别结果大不相同，但无论采用训练集数据仿真，还是测试集数据识别，本文构建的差分优化的加权复合多核核函数方法的状态识别正确率都明显高于传统RBF单核核函数和加权复合未作优化的多核核函数方法的正确率.

表2 不同SVM模型的变压器状态识别准确率对比Tab.2 Comparison of transformer state prediction results with the same data and different SVM models /%

5 小 结

本文基于支持向量机建立了电力变压器故障诊断模型，采用混合型特征量输入构建了加权复合多核核函数，利用差分进化算法进行复合多核核函数参数寻优.仿真结果显示：训练集故障诊断准确率为95.56%，测试集诊断准确率为94.44%，获得了较满意的高命中率变压器故障诊断效果.但本文的模型方法还有进一步改进、提升的空间：

1)本文采用混合型特征量输入，确实在一定程度上增加了特征的多样性，使得不同类别特征之间的差别更加明显，进而实现了更为清晰的分类效果.但本文采用的混合型特征量是否还有其他更好的混合形式、构成比例，是否还可以更本真地表现出变压器各状态之间的特征气体差异，还有待于进一步探究.

2)本文构建了加权复合多核核函数，原始数据可以较灵活地变换到适当的新空间，在新空间中可以实现较清晰地分划，但4种核函数不限类别地加权复合，对于所有状态，尤其是边界不太清晰的状态识别来讲，是否可以寻找到对复杂工况更具针对性的复合准则，使得本文方法更具普适性和可操作性，也有待于进一步探究.

3)本文利用差分进化算法进行复合多核核函数的参数寻优，获得了效果较好的状态分类.但除了差分进化算法外，是否还存在更具普适性和可行性的参数寻优方法，是否还存在更为适当的适应度函数方法，也还有待于进一步探究.

基于本文构建模型方法的有效性，下一步将继续围绕深度挖掘支持向量机模型各环节对变压器故障诊断准确度的影响，以及与其他人工智能模型方法结合的空间和可能性，寻找到更具普适性、更为有效的变压器故障诊断新方法.