高等数学中比较与反例教学方法探索——“以学生为中心”教学范式改革

庄 伟

（北京石油化工学院致远学院，北京 102617）

0 引言

高等数学是本科（理工、经管、人文）各专业的一门重要基础课，是高等本科院校教学计划中必不可少的一门重要主干基础课程。它还是服务于各专业的一门重要基础课，是培养学生应用数学知识解决实际问题的能力的有力工具。通过本课程的学习能使学生了解高等数学中的极限、导数与微积分等重要的基础概念的背景思想，较系统地掌握高等数学的基础知识、必需的基本理论和常用的运算技能，了解基本的高等数学的应用方法，为学生学习后继课程、专业课程和分析解决实际问题奠定基础。

高等数学的重要任务是将为今后学习专业基础课以及相关的专业课程打下必要的数学基础，为这些课程的提供必需的数学概念、理论、方法、运算技能和分析问题解决问题的能力素质。基于培养应用型工程师的特点，以及为适应迅猛的社会经济发展，为公司企业输送相应层次的技术人才，注重理论联系实际，强调对学生基本运算能力和分析问题、解决问题能力的培养，以努力提高学生的数学修养和素质，具体来说要具有逻辑推理能力、基本运算能力、自学能力、数学建模的初步能力、数学软件运用能力，应用数学知识解决实际问题的能力，从而使我们的大学生经一到两年的数学知识的系统学习，在理性判断、整体素质，特别是数学方面的素质能有一个明显地提升。

在教学过程中，新时代高等数学面临的难点：一是高等数学对绝大多数学生来说具有高度抽象性和理论性，概念和理论理解起来难，使学生存有“惧怕”心理；二是高等数学的知识点多，在学习的过程中前面所学的知识存在忘记了或不会用的现象，使学生对高等数学的知识无从下手，也不会用所学的知识点；三是部分学生认为“学高等数学”无用，有为了应付考试过关不得不学的心态，致使学习提不起兴趣来。这样如何让学生转变观念，不怕《高等数学》这门课程，让绝大部分同学对该课程感兴趣，使高等数学有吸引力和魅力，从而发挥《高等数学》这门课程的基础与服务作用就成了我们的教学难点。

1 “比较法教学范式”的引入

比较是我们经常使用的一种学习和思考形式，是笔者在以前的高等数学的教学过程中，比较法也是经常用到的教学方法，但是，比较法用得比较多的是例子和算法的比较，这对学生来理解和学习高等数学是很有帮助的，但所涉及的对概念、定理和性质的比较是不多的。这样我们的学生对算法和题型的比较就掌握得多些，也不感到陌生，而对概念理论的比较就涉及的少，认为概念、定理和性质都是固定不变的，这就使我们的学生“只知其然而不知其所以然”。而现在笔者在近几年的教学过程中，不但注重对学生的算法和题型的比较，而且笔者觉得对概念、定理和性质的比较对学生学习高等数学、理解高等数学的概念、定理和性质能更上一层楼。通过对几届学生的调查回访，学生觉得“比较法教学范式”是颇有收获的。当然对算法和题型的比较仍是我们课堂讲授的一个有效的手段，也是必不可少的。因此，笔者认为我们教师应在讲授的过程中把二者结合起来，即先对概念理论做比较，再对算法和题型做比较效果会更好，学生也更易接受，这样才能使学生不但知其然，也知其所以然。可目前的高等数学的教学中还存在注重“理论与计算”轻“教育过程”，即仅注重对概念、理论、计算方法和技巧的培养，而关注学生在学习过程中能获得什么不够，这样学生只能掌握知识的表面意义，不能了解数学知识背后深层次的意义。

“比较法教学范式”在这里我们分为单个知识点比较的教学模式──自己和自己的比较，和多个知识点比较的教学模式──前后不同的知识点作比较。我们的“单个知识点比较教学模式”从一开始讲授高等数学就开始了。

下面是数列收敛的概念：自变量取正整数n的函数称为数列，若其一般项的极限为一有限值a，则称数列收敛，否则称数列发散。数列收敛的几何解释为：当n充分大时，其一般项会落在值a的邻域内。

接着我们又给出了数列不收敛的概念：自变量取正整数n的函数称为数列，若其一般项充分大时会趋于不同的实数a，b，…等，或当n充分大时，其一般项趋于无穷，则称数列发散。数列发散从几何上来看表现为：当n充分大时，其一般项会落在多个值a，b，…等的邻域内，或其一般项会跑向无穷远。

因为课本和我们的授课内容中数列收敛的例子是比较多的，所以就着重给同学举了数列发散的如下的几个例子：

（1）一数列有两个不同的极限1和-1，符合数列发散的定义，所以数列发散；

（2）还有我们经常碰到的三角函数，如正弦函数和余弦函数也有不同的极限，不唯一，所以也不收敛；

（3）数列的一般项会变的无限大，跑向无穷远的情况，也不收敛。

（4）实际生活中的数列发散的例子，当学生人数很多的时候，如我们学生的学习成绩的趋向就是发散的，符合正态分布的，还有节假日外出旅游的客流量的趋向也是发散的。

这样，通过前面几节“比较法教学范式”的引入，很多同学觉得高等数学也没什么难的。

下面我们看多个知识点比较的教学模式──前后不同的知识点作比较。拿函数的极限和前面学过的数列的极限作比较，首先，当我们学习完函数极限的定义后，我们来和数列的极限作比较：

（1）数列的极限只有变量 趋于无穷这一种情形，即趋于无穷大；而函数的极限分 趋于某一有限值和无限 趋于无限，又分为正无穷和负无穷两种情形；

（2）函数的极限分为由左边逼近的左极限和由右边逼近的右极限两种情形，而数列极限无此情况；

（3）函数的极限存在必须是左极限等于右极限，而数列极限无此情况；

（4）函数极限既可等于此函数在该点的值，也可与函数在该点的取值无关，也与数列极限不同。

这样，通过做多个知识点比较学生就对这两种极限概念有了不同认识，分得清了也就会用不同的方法和理念来对待这两种极限，错误会明显减少了。

其二，在高等数学前面的授课内容中，当我们学了自变量趋于无穷大时函数的极限后，我们还做了关于函数极限的“单个知识点比较教学模式”，

（1）自变量 趋于有限值与自变量 趋于无穷大的比较；

（2）自变量趋于有限值时，函数极限存在；自变量趋于无穷大时，函数极限也存在；

（3）自变量趋于有限值时，函数极限存在；而自变量趋于无穷大时，函数极限不存在；

（4）自变量趋于有限值时，函数极限不存在；而自变量趋于无穷大时，函数极限存在；

（5）自变量趋于有限值时，函数极限不存在；自变量趋于无穷大时，函数极限也不存在。

对上述五种情况的函数极限，我们在定义、概念和例子上都作了横向的比较，这样，学生对所有情形函数极限都有了全面认识和体会，对函数极限这个重要知识点就能掌握了。

当然，后面的每一章我们都有“比较法教学范式”结合具体知识点的教学范式改革的案例，这里限于篇幅就不一一赘述了。总之，会让“比较法教学范式”贯穿高等数学学习的全过程。

2 “反例法教学范式”的引入

反例法在高等数学的教学实践中有着事半功倍的效果，也有着重要的作用。第一，恰当地运用反例法教学，能引导学生从反面去思考解决问题，从而有助于培养学生的逆向思维努力，提高学习效率；还有益于学生对基本概念的理解，使学生更好地掌握基本定理。第二，数学中的概念与定理有许多结构复杂、条件结论犬牙交错，使人不容易理解。反例则可以使概念更加确切与清晰，使定理的条件、结论之间的充分性、必要性指示得一清二楚。第三，高等数学中有许多反例，能够及时发现并有效地纠正习题中的错误，也能开拓学生的思维，培养学生的思维创新能力，引导学生多方面、多角度地思索问题。第四，反例法教学能帮助学生学习数学基础知识，提高他们的数学修养及培养他们对数学的兴趣，甚至还能让一些同学发现原有理论的局限性，对培养他们的科学研究能力及推动数学向前发展都是有好处的。

本文从引入反例，强化数学概念的认识与应用；巧借反例，在复习巩固中温故知新；运用反例，帮助学生正确判定命题的正确与否；借助反例，培养学生数学发散思维能力全方面发展，探讨了在高等数学教学中对反例教学开展的步骤策略，以期能引导学生从反面去思考解决问题，从而培养学生的逆向思维能力，提高高等数学的学习效率。

2.1 有助于学生理解并掌握课本上的基本定理

当我们讲完了函数的极限四则运算法则后，我们举了如下的反例：

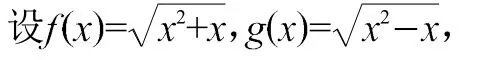
当求这两个函数差的极限时，若做成先求两个函数的极限再差，则这两个函数差的极限是不存在的，显然这是错误的，原因就是不符合函数的极限四则运算法则的如下的条件：

通过上面的反例，同学们明白了以后在思考问题及做作业、做题的时候括号是不能随便去掉的，反之会出现错误的。

2.2 有助于学生深化理解课本上的定理、性质及规则

当我们学到无穷小的比较时，对于无穷小的和差代替规则，我们举了如下的反例：若直接来用等价无穷小 x-x来代替是错误的。原因就是不符合无穷小的和差代替规则。

通过上面的反例，同学们就明白了课本上的定理、性质及规则是在什么条件下成立的，以及不当运用定理和性质所带来的错误。

2.3 有利于培养学生不断探索、勤于进取的良好学习习惯，也能提高大学生的数学素养和兴趣

当我们讲到初等连续函数的复合函数也是连续的时候，我们举了如下的反例：

先举了一个函数连续，另一个函数不连续的复合的反例，则无论是谁复合谁，在所给定的区间上都是不连续的；

又举了两个函数都不连续的复合的反例，也是无论谁复合谁，在所给定的区间上都是不连续的。

通过上面的反例，同学们就明白了初等函数的复合在什么情况下是连续的，又在哪些情况下是不连续的，这样就深化了学生对函数连续与否的理解和掌握，使高等数学的学习变的“看得见，摸得着”，既加强了学生学习高等数学的积极性和主动性，也提高教学效率。

这里我们仅举了上面几个“反例法教学”的例子，例如，还有有助于有效地纠正错误的反例，有助于开拓学生认识，培养学生创新能力的反例等等，这样的例子在每一章中我们都有结合具体知识点的教学范式改革的案例，这里限于篇幅就不一一赘述了。总之，会让“反例法教学范式”伴随学生高等数学学习的全过程。

3 总结

本文所探讨的“以学生为中心”的高等数学教学过程中“比较与反例教学方法”是笔者在高等数学方面实施的“以学生为中心”教学范式改革方面的一些做法和体会感受。我觉得在高等数学教学中，比较与反例教学方法应该引起我们教授高等数学教师的重视，合理恰当地运用比较与反例教学法进行教学，不仅可以激发学生的学习兴趣，深化学生对知识的掌握和了解，也可以让学生在比较与反例中发现、分析自己的错误，培养良好的数学思维，从而能提高学生的数学兴趣和素养。

在实施的过程中总体来看，高等数学课程的“比较与反例教学范式改革”还要在教法方法上精心设置教学案例，并以案例的比较、解决为中心。所选的案例要凸显高等数学的教学目标，提升学生的注意力。其次，建立丰富的交流和反馈渠道，加强师生之间、同学之间的交流，使教学更有针对性，培养学生的质疑能力。后面我们还要争取引入数学软件介绍和数学实验，能用数学软件来进行比较和列举反例，鼓励学生动手“做数学”：提供实验任务说明和实验指导。还要为学生提供精选的参考书目，指导学生充分利用身边的资源：图书馆，专家讲座、互联网搜索等等，针对自己关心的问题如何去寻找丰富的信息并做出筛选。对不同层次的学生提出不同的要求，成立兴趣小组引导学生形成良好的学习方法与学习兴趣。最后，建立和完善有效的评价和考试方式，最终目的是让学生觉得高等数学有用也有吸引力和魅力。