食饵具有避难所的离散种群模型的轨迹跟踪控制

付景超，唐 婕

(东北电力大学理学院，吉林 吉林 132012)

生态系统的捕食与被捕食行为是一种普遍的现象.自LOTKA和VOLTERRA建立数学模型[1-2]研究捕食与被捕食现象开始，许多研究人员对该模型进行了改进;WANG和PANG[3]考虑“比率依赖”理论，研究了混合比率依赖的三种食物链模型；SPROTT[4]由LOTKA-VOLTERRA模型衍生了多个捕食者的生物模型；DAS和CHAUDHURI[5]在捕食系统中引入疾病，研究了患病捕食者模型等.

事实上，捕食者的捕食效率很大程度上取决于被捕食者逃离捕食者的能力.通过避难所，部分猎物种群就得以被保护，免受捕食者的攻击.空间或时间避难所、聚集猎物或减少猎物的搜索活动等都可以被定义为避难所.为了研究避难所对捕食系统的影响，YAKUBU[6]研究了猎食保护区在多猎物离散系统中的影响，证明了这些物种在没有猎物庇护所的情况下会相互排斥；KRIVIAN[7]分析了避难所的保护性对LOTKA-VOLTERRA模型的稳定性的影响，并探究了如果捕食行为最佳，避难所是否能促进捕食者-猎物模型动态的持久性或稳定性；EDUARDO[8]等将猎物避难所纳入一个满足生物量转换原则的连续模型中，证明了从极限环到非零稳定点再到捕食者灭绝和猎物密度稳定的趋势，分析了两种避难方式的稳定域在参数空间上的差异；CRESSMAN和GARAY[9]通过一种进化生态学方法研究多物种捕食者-猎物生态系统稳定性，得到了避难所的存在增强了进化的稳定性和生态的稳定性的结论；HAUSRATH[10-13]等对不同的且带有食饵避难所的模型进行了动力学性质、分岔、混沌的研究，为后续的生物系统研究提供了基础.

近年来，对于混沌的控制研究也在生物学的多个方向得到了快速发展，CARMONA和FRANCO[14]研究了使混沌趋于渐近稳定平衡的比例反馈控制方法，还在种群动力学假设的条件下证明了该策略的一个优越性；张悦[15-17]等分别针对生物种群、广义生物经济系统、传染病动力系统进行了反馈线性化控制、混沌跟踪控制等多方面的混沌控制研究；KAR[18]于2005年考虑了一个包含猎物避难所且带有Holling Ⅱ型响应函数的捕食者-猎物模型，并对该模型进行了稳定性分析.

1 食饵具有避难所的离散种群模型的动力学性质

食饵具有避难所的离散种群模型[19]如下：

(1)

引理1[19]模型(1)存在3个不动点：

1)平凡不动点E0=(0，0)在任意条件下成立.

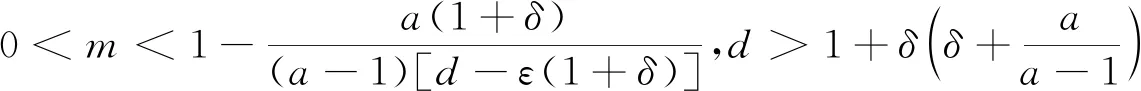
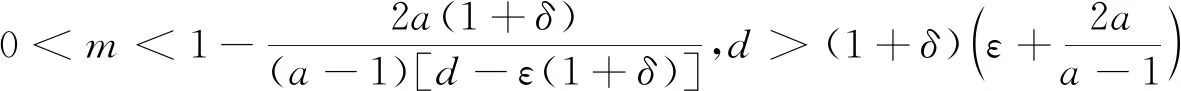
Lyapunov指数是用于识别混沌运动若干数值的特征之一，当LE>0时，相邻点最终按指数方式分离，这意味着运动轨道的局部不稳定，如果轨道有整体的稳定因素，则在此作用下反复折叠，形成混沌吸引子.

选取参数a=3.2、b=3.9，d=3.8、ε=0.01、δ=0.01、m=0.014，图1是m∈(0，0.014)的Lyapunov指数谱，观察发现系统(1)存在混沌运动.图2为a∈[1，4]的分岔图，发现该系统(1)存在混沌运动.

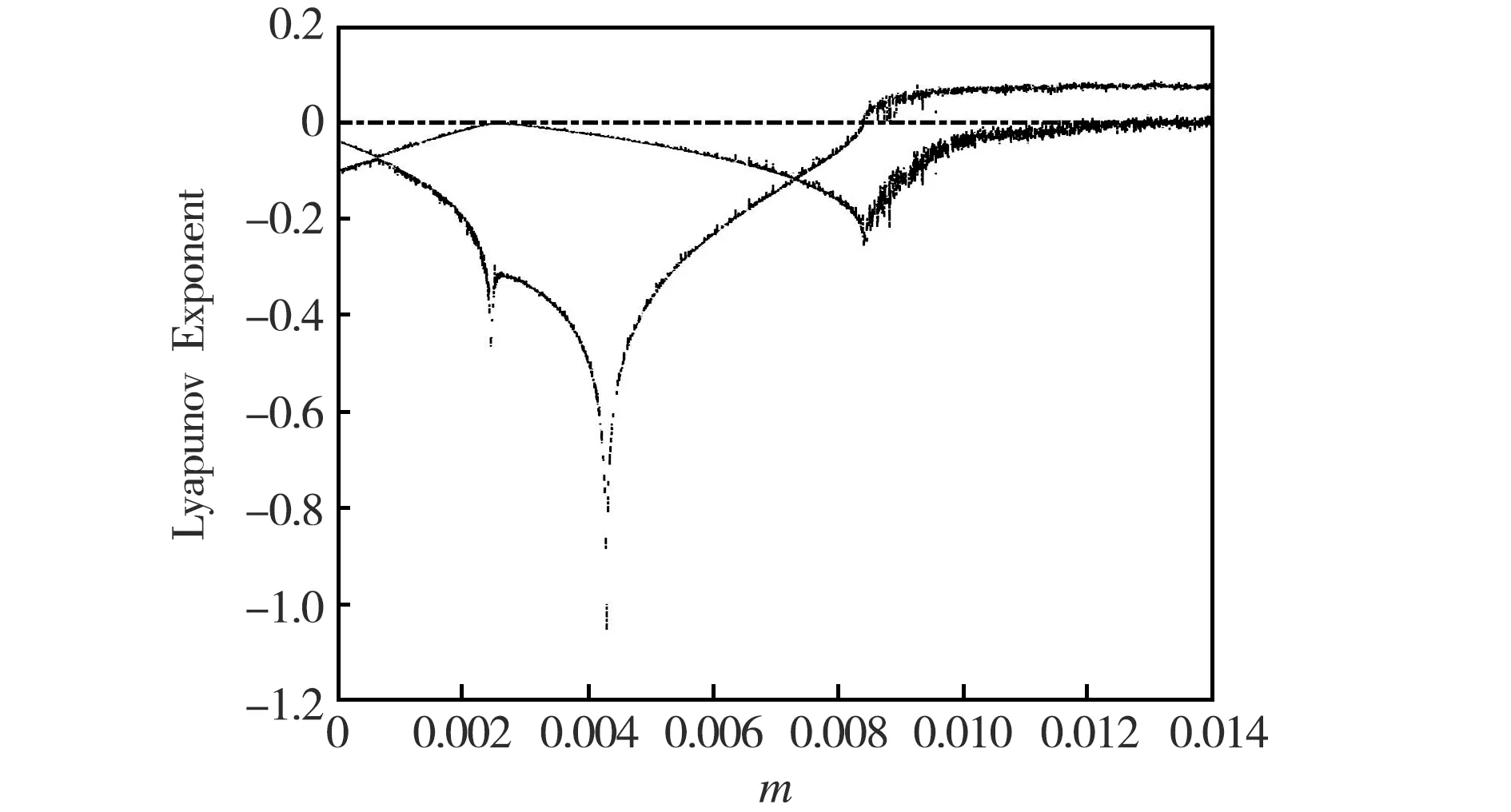
图1 系统(1)Lyapunov 指数图谱

图2 a∈[1，4]系统(1)分岔图

2 食饵具有避难所的离散种群模型跟踪控制

2.1 非线性反馈线性化混沌轨迹跟踪控制原理[20]

不失一般性，考虑单输入单输出输入输出可线性化系统

(2)

其中：ζ为n维状态向量；(Ac，Bc)是可控的；α(ζ)是状态向量ζ的连续可微函数向量；β(ζ)是状态向量ζ的非线性连续可微函数矩阵，β(ζ)在ζ定义域内是非奇异的.

对于不具有式(2)标准形式的输入输出可线性化系统可以通过微分同胚变换将其变换为式(2)的形式.

设计一个轨迹跟踪控制使输出y跟踪给定yR，并假定：

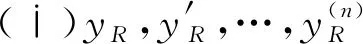
令

利用变量变换将式(2)转换为

(3)

取非线性状态反馈控制规律如下

可以将式(3)线性化为如下形式

(4)

对于式(4)所示的线性系统，设计一个状态反馈控制v=Ke，使得Ac+BcK为胡尔维茨(Hurwitz)矩阵，于是式(4)变为

(5)

式(5)为全局稳定的，而且通过选择不同的K可以控制跟踪误差的衰减率，从而保证跟踪效果.

这种方法采用非线性反馈将系统线性化为线性系统，再应用线性系统的设计方法设计轨迹跟踪控制，这种控制是全局收敛的.

2.2 非线性反馈线性化轨迹跟踪控制器设计

定理1系统(1)可以稳定到正不动点或周期轨道的充分条件是选择控制律Un：

证明：根据上述非线性反馈线性化混沌轨迹跟踪控制原理，对模型(1)加入控制器

(6)

其中Un=[u1n，u2n]T为控制输入的外部控制信号.当u1n=u2n=0时，则系统(6)等价于系统(1).

达到的目的是控制系统的混沌轨道到正不动点E*=(x*，y*)，所以令

那么系统(6)变为

Xn+1=AXn+F(Xn)+Un

，

(7)

其中：A为G(Xn)的线性部分的系数矩阵；G(Xn)的非线性部分为F(Xn)；Un=[u1n，u2n]T为外部控制信号.

现在假设

(8)

Un=U(n)=Xr(n+1)-AX(n)-F(Xn)+ken

，

(9)

即

结合式(7)～(9)有

e(n+1)=ke(n)

，

选择|k|<1，则闭环系统的误差e(n)渐近稳定到平衡点e(n)=0，系统可以达到给定的跟踪控制.证毕.

3 数值仿真

选取参数a=3.2、b=3.9、d=3.8、ε=0.01、δ=0.01、m=0.014，系统(1)呈现混沌状态.

选取正不动点E*=(0.270 3，0.351 6)作为理想的控制轨道，将Un施加在系统(1)上，如图 2和图 3所示，经过2 000 次迭代后，系统(1)的混沌状态将很快稳定到正不动点，其中k=0.1.

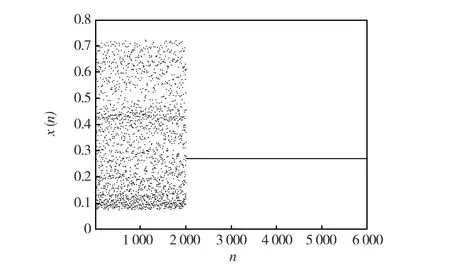
图3 跟踪控制变量x(n)到正不动点x*

如图5和图6所示，选择预期的周期函数

图4 跟踪控制变量y(n)到正不动点y*

图5 跟踪控制变量x(n)到给定周期轨道

图6 跟踪控制变量y(n)到给定周期轨道

在2 000 次迭代之后对系统(1)施加控制Un，系统可以跟踪给定的预期的周期函数，表明了混沌轨迹跟踪控制方法的有效性.

4 结 论

本文对食饵具有避难所的离散种群模型进行了混沌控制研究，得出了以下结论：

1)利用Lyapunov指数谱和分岔图验证了食饵具有避难所的离散种群模型中存在混沌现象.

2)通过数值仿真验证了根据混沌轨迹跟踪控制原理设计的控制器的有效性.

3)为后续多维食物链模型研究提供理论基础，对保持生态平衡及可再生资源持续利用有一定的理论与应用价值.