可解释的知识图谱推理方法综述

2022-11-19夏毅兰明敬陈晓慧罗军勇周刚何鹏

网络与信息安全学报 2022年5期

夏毅，兰明敬，陈晓慧，罗军勇，周刚，何鹏

可解释的知识图谱推理方法综述

夏毅，兰明敬，陈晓慧，罗军勇，周刚，何鹏

（信息工程大学，河南郑州 450001）

近年来，以深度学习模型为基础的人工智能研究不断取得突破性进展，但其大多具有黑盒性，不利于人类认知推理过程，导致高性能的复杂算法、模型及系统普遍缺乏决策的透明度和可解释性。在国防、医疗、网络与信息安全等对可解释性要求严格的关键领域，推理方法的不可解释性对推理结果及相关回溯造成较大影响，因此，需要将可解释性融入这些算法和系统中，通过显式的可解释知识推理辅助相关预测任务，形成一个可靠的行为解释机制。知识图谱作为最新的知识表达方式之一，通过对语义网络进行建模，以结构化的形式描述客观世界中实体及关系，被广泛应用于知识推理。基于知识图谱的知识推理在离散符号表示的基础上，通过推理路径、逻辑规则等辅助手段，对推理过程进行解释，为实现可解释人工智能提供重要途径。针对可解释知识图谱推理这一领域进行了全面的综述。阐述了可解释人工智能和知识推理相关概念。详细介绍近年来可解释知识图谱推理方法的最新研究进展，从人工智能的3个研究范式角度出发，总结了不同的知识图谱推理方法。提出对可解释的知识图谱推理研究前景和未来研究方向。

知识推理；知识图谱；可解释人工智能；信息安全

0 引言

随着信息技术的不断发展，人工智能实现了从能存会算的“计算智能”，到能听会说、能看会认的“感知智能”[1-3]，再到下一阶段具备理解、推理和解释能力的“认知智能”[4-6]的逐渐演变，这3个阶段的实现难度和价值同时逐次提升。然而，在以深度学习为主导的人工智能技术中，大多数的模型是不透明的，即模型在产生高精度结果的同时，不能提供必要的解释过程。模型的不可解释性严重影响了人们对模型决策的信任程度，其可靠性和鲁棒性均受到广泛质疑[7]，特别在国防、医疗和网络与信息安全等领域的许多关键应用[8-11]中，保证系统所做出的决策具备透明性和可解释性是非常重要且必要的。

知识推理是人类智能活动的重要组成部分，一直以来也是人工智能的核心研究内容之一。DeepMind指出人工智能算法必须具备推理能力，且推理过程需要依靠人的先验知识[12]，对推理的结果形成必要的解释。作为目前知识推理最新的知识表达方式，知识图谱[13]技术是一种实现可解释人工智能的可能解决方案[14]，通过将不同数据源中的数据统一结构，实现对多源信息的语义网络建模，为真实世界的各个推理任务提供概念、关系和属性等可解释因素。

以安全领域的知识图谱为例，该领域主要包括网络空间测绘图谱、漏洞知识图谱、恶意样本知识图谱、攻击路径推理图谱等。通过威胁建模的方式，对多源异构的网络安全领域信息进行加工、处理、整合，转化成为结构化的安全领域知识库，实现从威胁实体和关系的视角出发，识别威胁以及对威胁进行评估。同时，在从图谱海量数据中挖掘、推理威胁的实体相关信息过程中，只有通过可解释的知识推理方法，才能进一步为推理结果的安全可靠提供保证，提高威胁分析的效率。

在长期的研究和实践过程中，研究人员相继总结了有关知识图谱推理的不同技术，并尝试从不同的角度（如推理长度[15]、分布式表示[16]、图嵌入[17]）对推理模型进行综述。然而，对于推理模型的可解释性则缺少相关的总结与对比。同时，人工智能的可解释性越来越受到人们的重视，可解释知识推理在近几年的学术界和工业界中逐渐成为关注热点，知识推理领域缺少较为全面且详细的针对可解释知识图谱推理的综述文章。

本文通过广泛整理与可解释知识图谱推理相关的文献，在介绍相关知识推理的基本概念及可解释性定义的基础上，从人工智能研究范式的角度出发，详细阐述符号主义中的可解释知识图谱推理方法、行为主义中的可解释知识图谱推理方法、连接主义中的可解释知识图谱推理方法和新型混合的可解释知识图谱推理方法，详细说明了在不同场景下，各类可解释知识图谱推理方法的核心思想及改进过程。本文还讨论了可解释知识图谱推理的未来研究方向及前景。

1 可解释的知识图谱推理概述

1.1 可解释性的定义

目前业界较为认可的可解释性定义为“可解释性是一种以人类认识、理解的方式给人类提供解释的能力”[5]。

虽然人工智能技术不断取得突破性进展，高性能的复杂算法、模型及系统却普遍无法向人类用户解释它们的自主决策和行为，缺乏决策逻辑的可解释性[18]。如图1所示，很多机器学习方法在模型性能和可解释性之间存在不平衡现象，往往模型越复杂越难以解释[14]，这对模型后期的应用和优化产生很大的影响，因此人们大多基于经验来调整模型参数以达到优化模型的目的[19]，然后通过观察结果来判定操作的正确与否，充满盲目性与随机性，忽略了模型可解释性的重要性。

可解释性对于用户有效地理解、信任和管理人工智能应用至关重要[6]，它与深度神经网络中“黑匣子”的概念形成鲜明对比。不可解释的模型在实践中经常出现难以预测正确结果的情况，这在低风险的环境中，不会造成严重后果（如视频推荐系统），而对于可靠性要求较高的系统则很危险[20]（如医疗、法律和信息安全领域），模型必须解释如何获得相关预测。可解释人工智能（XAI，explainable artificial intelligence）则提供了一种信任的基础，在此基础上，人工智能才能在更大范围发挥作用，有助于识别潜在的错误，进而改进模型[4]，提高信息服务质量，满足道德和法律的规范要求，为用户提供更智能的服务。

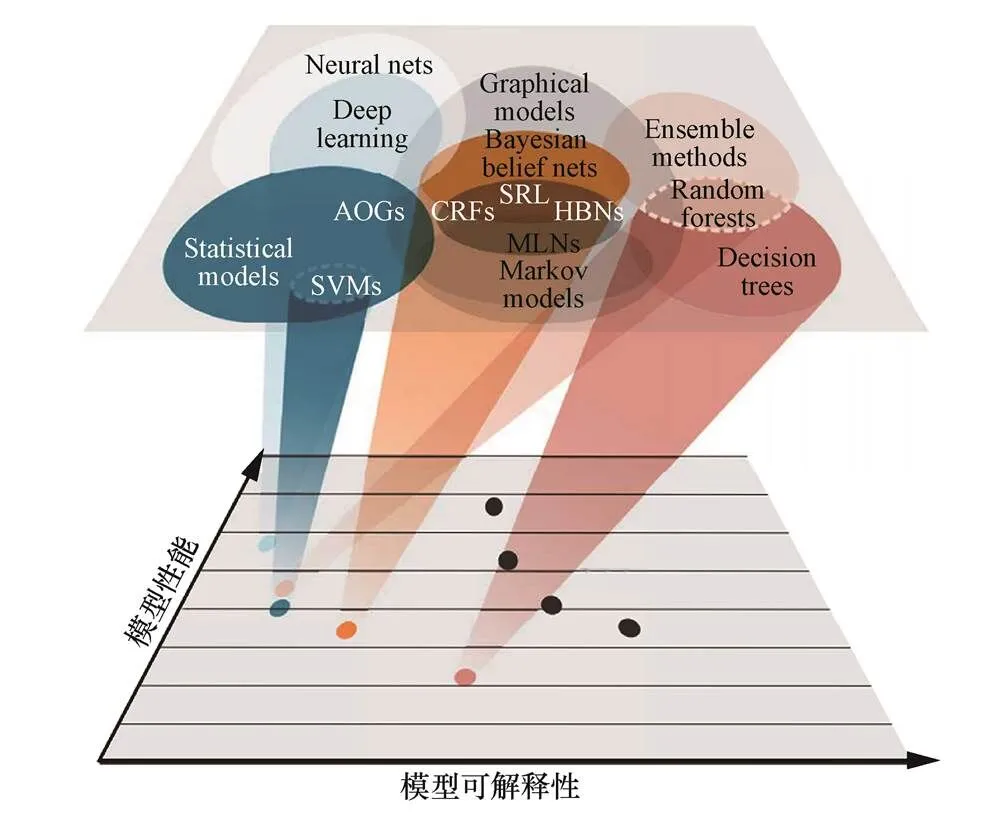
图1 机器学习模型的可解释性与性能对比

Figure 1 Interpretability and performance comparison between machine learning models

1.2 知识图谱及相关推理任务

知识图谱是人工智能的核心技术之一[13]，作为一种新型的知识表示方法，知识图谱中包含大量的先验知识，并以结构化三元组的形式组织海量信息，通过实体和关系的形式将不同的数据源进行关联和深度融合。目前，大量的知识图谱，如Yago[21]、Dbpedia[22]和Freebase[23]已经开发，相关技术已被广泛应用在智能问答[24]、推荐系统[25]和信息安全[26]等任务中，其突出表现在学术界与工业界均获得了广泛关注[27-28]。网络空间知识图谱示例[29]如图2所示。

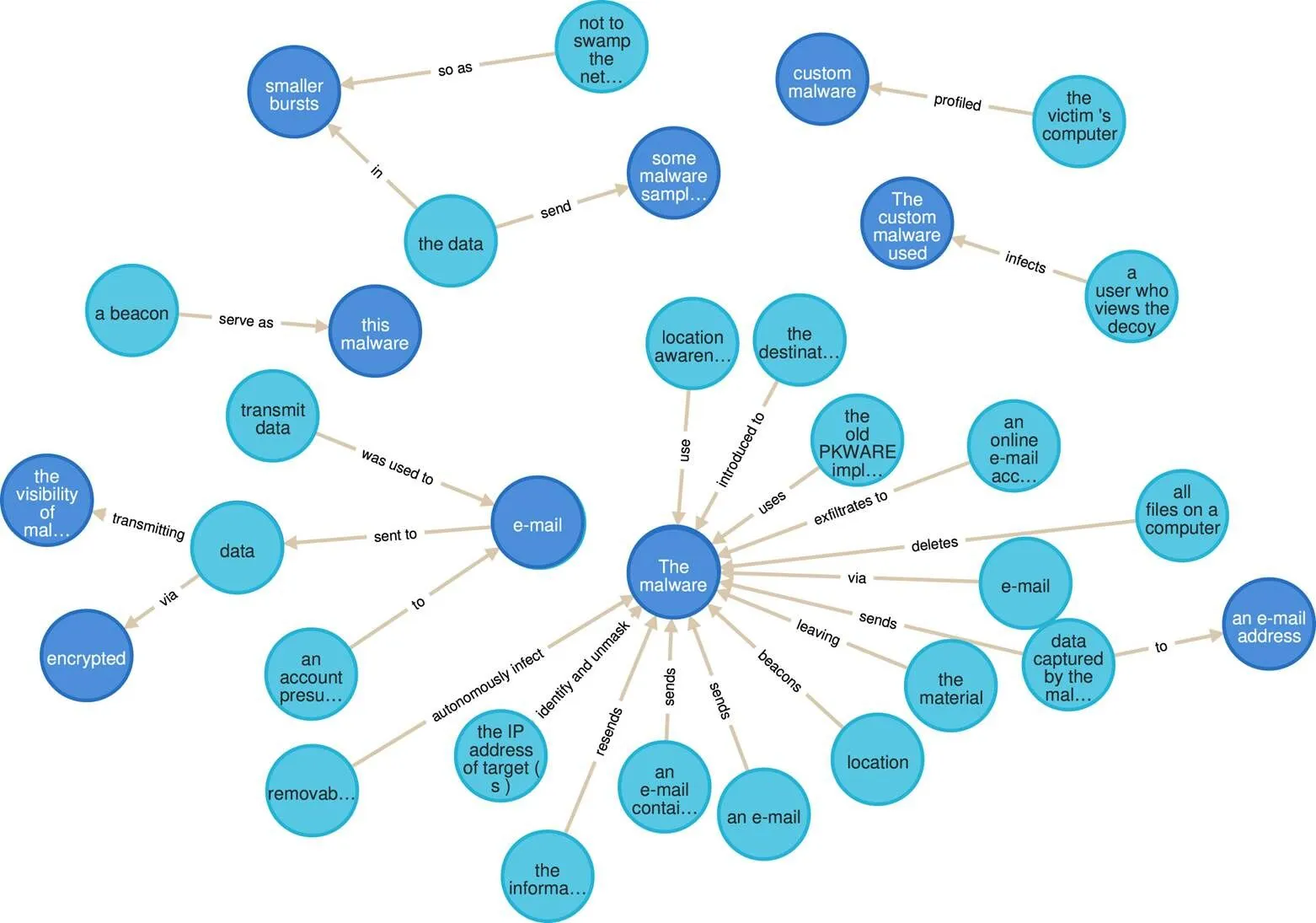
图2 网络空间知识图谱示例

Figure 2 An illustration of cyber security knowledge graph

知识推理[15]则是从已知的知识出发，经过推理挖掘，从中获取所蕴含的新事实，或者对大量已有知识进行归纳，从个体知识推广到一般性知识的过程。早期的推理研究大多在逻辑描述与知识工程领域，很多学者提倡用形式化的方法来描述客观世界，认为一切推理是基于已有的逻辑知识，如一阶逻辑和谓词逻辑，如何从已知的命题和谓词中得出正确的结论一直是研究的重点。近些年，随着互联网数据规模的爆炸式增长，传统的基于人工建立知识库的方法不能适应大数据时代对大量知识的挖掘需求。数据驱动的推理方法逐渐成为知识推理研究的主流[30]。

面向知识图谱的知识推理即在知识图谱的图结构上，结合概念、属性和关系等知识，通过相关推理技术，进行知识推理的过程。知识图谱中所包含的概念、属性和关系天然可用于解释[31-32]，且更符合人类对于解释的认知，方便为真实世界的推理和解释场景进行直观建模，因此当前基于知识图谱的知识推理方法成为知识推理领域的典型代表。下文中的“知识推理”如未加特别说明，特指“面向知识图谱的知识推理”。

知识图谱推理任务主要包括知识图谱补全和知识图谱去噪。前者是通过推断出新的事实，扩充知识图谱，包括实体预测、关系预测、属性预测等任务。其中最为核心的任务是实体预测和关系预测，实体预测是指利用给定的头实体和关系（或者关系和尾实体）找出有效三元组的尾实体（头实体）；关系预测是指通过给定头实体和尾实体，推理出两者间的关系。后者关注图谱中已知的知识，对于已经构建的图谱中三元组的正误进行评判，但从本质上来讲，两者其实是在评估三元组的有效性。除此之外，知识推理在下游的信息检索、智能问答和推荐系统中也发挥着重要的作用，在智慧医疗、网络与信息安全等领域显现出良好的应用场景[27-28]。

1.3 基于知识图谱的可解释知识推理

知识推理的可解释性或者可解释的知识推理，是人工智能可解释性的子问题[33]。与研究深度学习算法的可解释性不同，可解释知识推理的目的是从已知的知识出发，经过可解释的推理方法，最终获取知识库中蕴含的新知识。目前基于知识图谱的可解释知识推理是该领域前沿的研究方向之一，其在可解释知识推理上有诸多优势，具体如下。

首先，知识图谱在表示模式上具有可解释优势。知识表示是为描述世界所做的一组约定，是知识的符号化、形式化或模型化的过程。常见的知识表示方法包括谓词逻辑表示法、产生式表示法和分布式知识表示法等，作为一种新型的知识表示方法，相对于这些传统的知识表示方法，如产生式表示法，知识图谱具有语义丰富、结构友好、知识组织结构易于理解的优点。

其次，基于知识图谱的推理在推理过程中具有可解释的优势。人类认识世界、理解事物的过程，大多是在利用概念、属性、关系进行理解和认知，如对于问题“为什么鸟儿会飞？”，人类的解释可能是“鸟儿有翅膀”，这实质上使用了属性来解释。知识图谱中富含实体、概念、属性、关系等信息，通过图结构形式化组织这些海量的知识，为真实世界的各个推理场景直观建模，可以对最终的决策进行更多元的具体解释。

最后，知识图谱在存储和使用上具有可解释的优势，相比其他的存储形式，知识图谱以三元组的形式对知识进行构建以及存储，更加接近人类通常认识事物“主谓宾”的认知和学习习惯，对于人类理解会更加友好，对人们的可解释性相比其他知识表示方法较强[19]。

1.4 知识推理任务的评价指标

1.4.1 知识推理可解释性的评价指标

本文采用的知识推理的可解释性评价指标如下。

（1）可解释的范围

根据模型产生的可解释性范围，可解释性分为局部可解释和全局可解释，即解释是面向某个或某类实例还是面向整个模型行为。

（2）可解释的产生方式

根据模型解释产生的方法，推理模型可以分为事前可解释和事后可解释。其中，事前可解释主要指不需要额外辅助的解释方法，解释本身就在自身的模型架构中，而事后可解释指解释本身不在模型架构中，而是在模型训练后，以人类可理解的规则或可视化等方式，对模型做出决策的逻辑过程进行后验的解释。

图3 可解释的知识图谱推理方法分类

Figure 3 Classification of explainable knowledge graph reasoning methods

（3）可解释的泛化性

根据解释方法是否特定于模型，可以划分为特定于模型和与模型无关两种解释类别。

（4）可解释在下游场景的适用性

根据下游实际业务需求对于知识推理方法的可解释性的要求，可以将推理方法分为适用于可靠性优先领域（如医疗、网络与信息安全领域）和适用于效率优先领域（如电影推荐系统）。本文在接下来综述方法时，每类方法根据以上4种评价指标对模型的可解释性进行对比分析。

1.4.2 知识推理准确性的评价指标

本文采用的知识推理的准确性评价指标包括平均倒数排名（MRR，mean reciprocal rank）和前次命中正确预测结果的比例（Hit@）。这两个指标均是国际通用的搜索算法评价标准，具体计算方法如下：

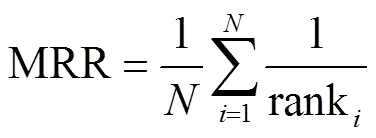
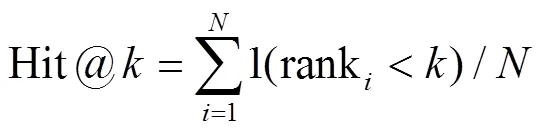
其中，表示查询的数量，对于一个查询来说，rank表示第一个相关结果的排序位置。

在相关模型准确率评测的过程中，本文在同一实验环境（FB15K-237数据集）下，对综述的各类知识图谱推理方法准确率进行量化评测。

2 可解释的知识图谱推理方法

推动人工智能发展的3种主要研究范式（符号主义、行为主义和连接主义），对知识图谱推理方法都有着很大的影响，但三者在研究方法和技术路线等方面有着不同的观点，导致不同研究范式影响下的知识推理方法在可解释性与效率上存在不同的侧重，所适用的应用场景有所差异。如图3所示，本文从这3种研究范式角度出发，结合目前新型混合的知识图谱推理技术，分别综述这些分类中最新的可解释知识图谱推理方法研究进展。

2.1 符号主义中的可解释知识图谱推理方法

从符号主义角度，知识推理可以建模为依据符号表征的一系列明确推论，通过显式的定义推理所需要的本体概念、规则等离散符号，进行逻辑推理的过程。其核心是从实例中推导出一般的本体演绎关系或逻辑规则，通过符号体系进行推理，同时，这些符号体系为推理结果提供显式的解释。根据知识图谱本体概念层和实体实例层的划分，符号推理方法可以分为基于本体的知识推理和基于逻辑规则的知识推理，接下来分别介绍其中有代表性的可解释知识推理方法。

2.1.1 基于本体的知识推理

本体是用于定义事物类型及属性的广义语义模型。基于本体的知识推理方法主要在抽象化的本体层通过频繁挖掘模式等方式进行推理，运用本体中的知识来辅助解决涉及语义的应用。用户可以结合已有的本体知识清晰地了解推理的过程与步骤，具有较强的可解释性。

知识图谱本身就可以理解为规模非常大的本体[34]，存储着大量的实例三元组。虽然本体本身没有正式的语义，但可以通过应用Web本体语言（OWL，Web ontology language）或资源描述框架（RDFS，resource description framework schema）等本体语言对概念进行描述[35]，从而进行知识的表示和推理[36]。Zou等[37]提出一种推理机F-OWL，F-OWL使用基于OWL的框架进行推理，该框架支持对知识库的一致性检查。为进一步提高该类方法的效率、支持更复杂的知识推理，Sirin等[38]提出了OWL-DL推理机Pellet，Pellet通过导入规则进行推理增量地更新知识，同时支持对动态知识进行迭代更新。Wei等[39]提出并实现了一种分布式推理规则的知识图谱推理系统KGRL，KGRL可以更好地表达规则，具有更强大的推理能力，同时KGRL通过相关优化过程，消除冗余数据，使推理的过程更加清晰准确。

以上基于现有本体演绎关系实现的本体推理，不同类型的本体和规则类型有多种组合，运算复杂度会呈指数级上升。为了提高基于本体推理方法的效率，进而对大规模知识图谱有更好的扩展性，很多学者在不同方面进行了努力。Zhou等[40]提出了一个用于大规模OWL的推理系统Minerva，Minerva结合了描述逻辑推理器和规则引擎进行本体推理，提高了效率。为了提高推理的可扩展性和性能，Soma等[41]提出了一种并行化的OWL知识库推理方法。通过对知识库进行划分，实现不同规则子集并行化应用于知识库。Marx等[42]提出了一个更简单的、基于规则的多属性谓词逻辑片段推理方法，可进一步用于大型知识图谱的本体推理。Chen等[43]则在此基础上提出了本体路径发现（OP，ontological pathfinding）算法，通过一系列的并行化和优化技术扩展知识图谱的规模，用发现的规则进一步扩充知识图谱，如图4所示，实线代表知识图谱中已有的知识，以事实三元组的形式进行存储；虚线代表通过OP算法中本体间上下位的规则，可以推理出的潜在事实三元组。该算法运用一种新的分割方法，通过继承上位词的关系得到封闭模式图，将挖掘任务分割成更小的独立的子任务，同时通过规则修剪策略，检测不正确的和消耗资源的规则，在每个部分构建置信度高的候选规则集。

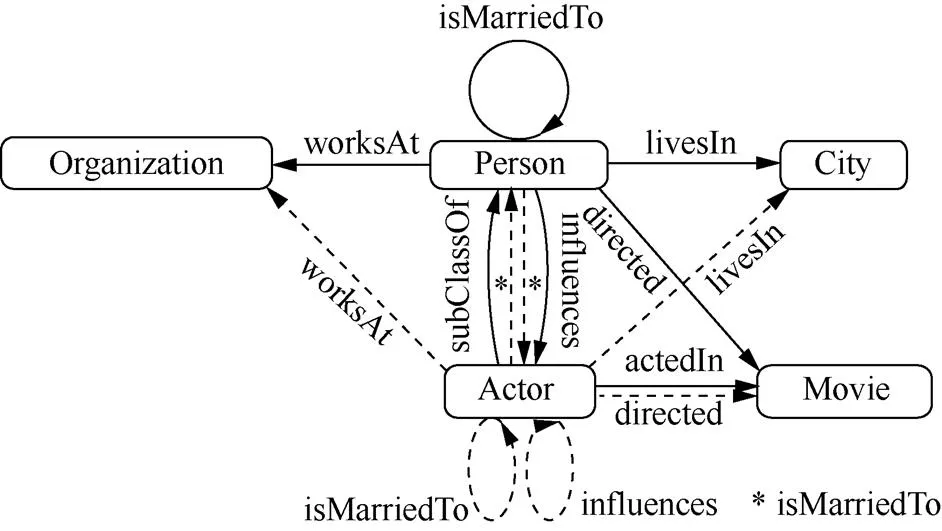
图4 OP算法中封闭模式图实例

Figure 4 Example schema closure graph in OP algorithm

近些年来，很多学者尝试对概念层的本体进行表示学习，即本体嵌入[44]，来进一步提高本体推理的效率。本体嵌入考虑的是本体语义和逻辑层面的表示学习，其更关注表示概念层的层次体系、概念之间的逻辑组合关系、属性的层次体系、概念和属性之间的逻辑组合关系。其中比较典型的本体嵌入模型是EL Embedding[45]，其基本思想是将本体中每一个类映射成一个球的几何表示，而类之间的关系可以用球的位置反映，进而实现概念层的推理。该类模型的主要目标是将类和属性之间逻辑关系映射到向量空间，并在向量空间完成类似逻辑空间完成的本体概念推理[46]。

基于本体的知识推理在推理过程中有很多本体约束，且大部分推理场景为自上而下的演绎推理，可以利用抽象本体层面的频繁模式或路径进行推理，为相应的知识推理提供较高准确率，同时这些约束会反映推理出结果的过程，提高推理的解释性。由于抽象层面的本体需要进行相应的实例化，对于实例数量较多、规模很大的知识库，推理的可计算性一般比较差，效率比较低，并且这类知识推理方法的鲁棒性差，高度依赖于本体约束的准确性，当数据存在噪声时，会误导推理结果。

2.1.2 基于逻辑规则的知识推理

基于逻辑规则的知识推理方法通过人工定义或结合机器学习等方法自动化地发掘规则和特征，结合合适的剪枝策略，进一步应用于推理任务。逻辑规则可以提供清晰、明确的推理依据[6]，因此具有较强的可解释性。早期的基于一阶谓词逻辑的推理方法较为经典。为进一步实现具有不确定性的大范围知识推理，适应更加复杂的推理环境，学者相继提出很多概率规则推理方法。

（1）基于一阶谓词逻辑的知识推理方法

在早期的推理研究中，知识推理主要依靠一阶谓词逻辑，通过设置关系推理的逻辑和约束条件，实现执行简单的推理。其中较为经典的是由Schoenmackers等[47]提出的一阶归纳学习器（FOIL，first-order inductive learner），其目的是搜索知识库中的所有关系，获取每个关系的霍恩子句集合作为特征模式来预测推理结果。在此基础上，为进一步提高推理的准确率，Landwehr等[48]提出的 nFOIL和tFOIL分别在FOIL基础上集成了朴素贝叶斯学习方法和树状增强的朴素贝叶斯方法，对学习器的搜索进行指导。Landwehr等[49]提出的 kFOIL结合了FOIL的规则学习算法和核方法，从其关系表示中得到特征的集合，将这些特征用于核方法，进行更高效的预测。

传统的FOIL算法成功实现了在小规模的知识库中有较高的推理精度，但由于实体和关系的复杂性和多样性，并且随着动态添加新的事实三元组，扩展规则的复杂度会呈现指数级上升，其高复杂度和低效率使原始的FOIL算法不适用于目前的大规模图谱的推理。为了缓解这个问题，Nakashole等[50]提出了一种结合软演绎规则和硬规则的RDF知识库查询一阶推理方法，软规则用于产生新事实，而硬规则用于强制知识图谱中的数据和推断事实之间的一致性约束。在归纳效率方面有较大进展的是Galárraga等[51]提出的AMIE系统，AMIE从以下两个步骤进行挖掘逻辑规则。首先是规则扩展，通过3种给定操作（添加悬挂边、实例边和闭合边）扩展候选的规则；然后通过规则修剪，去除其中错误的规则，并根据预定义的评估指标输出可信规则。

为进一步提升逻辑规则的归纳速度，以适应目前大规模的知识库，Galárraga等[52]进一步在AMIE的基础上通过增加一系列的剪枝算法和查询重写技术，将AMIE扩展为AMIE+，通过考虑实体类型信息并使用联合推理，在推理速度和预测的精度上有了大幅度提升。然而，AMIE+每次只能挖掘一条规则，无法进行并行化。为进一步提升推理的并行效率，Wang等[53]提出了一种新的规则学习方法RDF2Rules，RDF2Rules通过挖掘频繁谓词的方法来并行化这个过程，凭借适当的剪枝策略，实现更有效地在大规模的知识图谱上进行推理。

（2）基于概率规则的知识推理方法

一阶谓词逻辑表示的方法是以谓词公式的形式为结果的，其规则的逻辑值只有“真”和“假”两种结果，而对不确定性的知识无法表示，所以其仅适用于精确性知识推理方法，而不适用于表示具有不确定性或模糊性的知识推理。因此，研究人员提出了基于概率规则的知识推理方法，通过结合一阶谓词逻辑和概率图模型，同时应用逻辑规则或统计特征来进行建模，实现具有不确定性的知识推理，扩充符号逻辑推理的功能。其中较为典型的方法是Richardson等提出的马尔可夫逻辑网络（MLN，Markov logic network）[54-56]。如图5所示，MLN模型基于定义好的规则和知识库中的事实三元组建立概率图模型，在建立的马尔可夫逻辑网络中应用马尔可夫链蒙特卡洛（MCMC，Markov chain Monte Carlo）算法，通过最大似然估计[55]学习对应规则的权重，进而在给定周围事实的情况下推断未知三元组成立的概率。

然而，在MLN模型中，计算目标实例的概率需要所有符合相关规则的实例，这在现实的应用中很难得到满足。De等[57]提出的ProbLog模型则通过选择性线性确定（SLD，selective linear definite）的方法为查询建造推理树来解决这个问题，通过自上而下的方式构建SLD搜索树，将目标查询的概率最终分解为计算所有可能子句集合的联合概率总和。为进一步优化计算子句的速度，Cussens等[58]提出随机逻辑程序（SLP，stochastic logic programs）方法，SLP定义了一个遍历SLD树的随机过程，其中节点上定义的概率分布通过对所需答案子句和其他子句进行加权求和来学习。Wang等[59]提出的ProPPR方法则对SLP进一步进行扩展，将SLP随机抽样策略改为基于个性化的PageRank算法[60]的偏差抽样策略，从而实现优化推理速度。

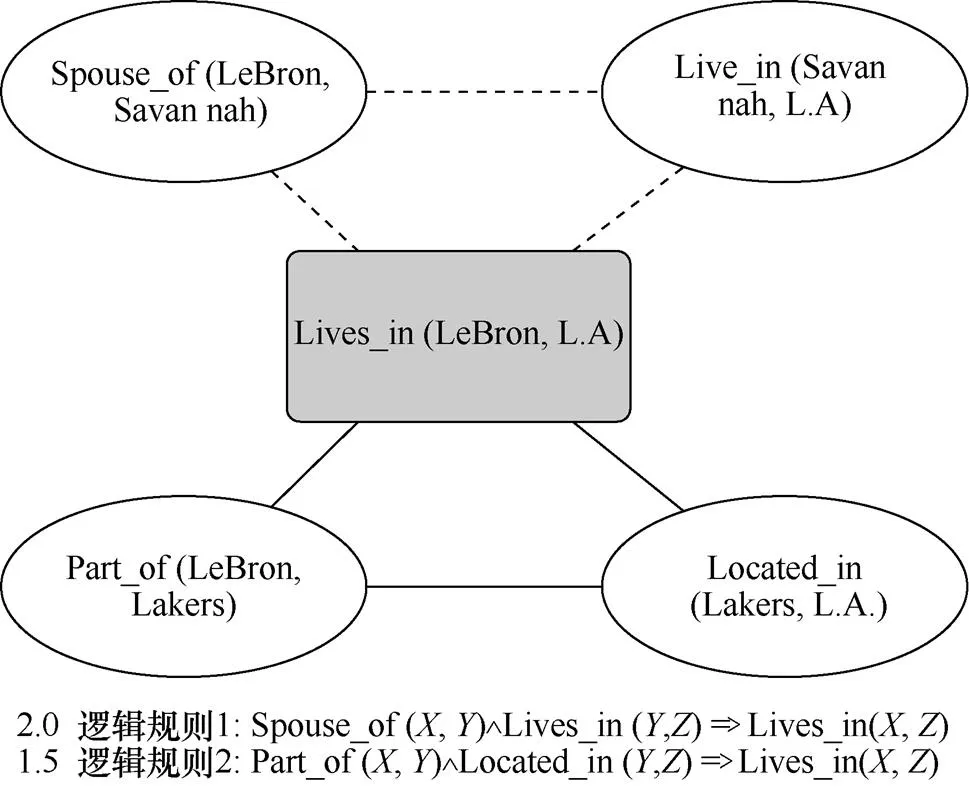
图5 马尔可夫逻辑网络推理模型[54]

Figure 5 Reasoning model based on Markov logic network[54]

以上方法均在假设数据完整的情况下进行推理，数据的缺失会导致其赋值各种组合公式学习和推理难以优化。为了解决这一问题，Kimmig等[61]提出了概率软逻辑（PSL，probability soft logic）。PSL使用FOIL规则作为在软真值区间为[0,1]的随机变量，在这种情况下，推理可以被认为是一个持续优化的任务，可以有效地在数据缺失的情况下进行运算。为进一步优化在缺失数据情况下的推理速度和准确度，Pujara等[62]通过生成一个以实体和关系为节点、本体约束为边的知识图谱，采用边缘最小切割聚类技术对关系和标签进行划分，利用PSL定义的联合概率分布，实现并行高效推理。Bach等[63]在此基础上提出了一种能在更大规模知识图谱中进行推理的方法——Hinge-Loss马尔可夫随机场（HL-MRF）模型，它实现了基于布尔逻辑的松弛概率推理和基于模糊逻辑的精确概率推理，使模型在离散和连续的数据中都可以实现高效推理。近些年，利用强化学习进行规则归纳的方法也有一定的进展，Meilicke等[64]提出的AnyBRUL模型利用强化学习的方法对两个实体间的关系进行采样，然后从采样路径中构造基本规则，并根据自下而上的规则构建方法将频繁路径模式一般化为抽象规则，取得了效率的一定提升。

总体来说，符号主义的知识推理具有严谨的推理过程，其依据的本体演绎关系或逻辑推导规则可以为推理结果提供可解释依据[65]。具体地，如表1所示，在可解释性的范围方面，符号主义中的知识推理方法通过概念层的本体演绎关系，或图谱中逻辑规则的挖掘进行解释，解释不单单针对某一个或一类实例，因此具有全局可解释性；在可解释性的产生方式方面，模型的解释通过本身的本体和逻辑规则，不依赖于模型以外的辅助方法，因此其解释性产生方式均是事前可解释的；在可解释性的泛化性方面，推理出的本体演绎关系和规则不特定于具体模型，所以解释与模型无关；在可解释的下游场景适用性方面，该类推理方法适用于可靠性优先领域。

表1 符号主义中的可解释知识图谱推理方法

注：由于符号主义中基于本体的知识推理为概念层的推理，推理准确性不做比较。

2.2 行为主义中的可解释知识图谱推理方法

从行为主义角度，知识图谱推理可以建模为在图结构上通过多步游走，同时对每一步进行预见和控制，通过序列决策逐步找到推理答案的过程，其核心是实现知识图谱图结构上的多跳推理。该类方法在得到推理结果的同时，显式地推导出具体的路径推导过程，因此可解释性较强。

该研究领域有两个主要方向，分别是基于随机游走和基于强化学习的知识图谱推理方法。基于随机游走的知识图谱推理方法在图结构上利用随机游走策略，结合合适的图搜索算法获取多条路径，利用这些路径的特征预测实体间是否存在潜在的关系；基于强化学习的知识图谱推理方法则通过智能体与环境不断进行交互，以反馈和交互的方式训练智能体，在动作选择和状态更新的动态过程中逐渐优化目标，进而实现知识推理。

2.2.1 基于随机游走的知识推理

基于随机游走的方法将路径作为特征对推理结果进行预测，由于路径的特征是可解释的，人们更容易理解其含义，通过对路径的重要性进行量化，来判定特征对最终预测结果的影响。具体地，Lao等[66]提出的路径排序算法（PRA，path ranking algorithm）是其中较为经典的基于随机游走的知识推理方法，为了学习数据库中特定边缘类型的推理模型，PRA首先游走发现边缘类型序列，通过逻辑回归模型，将这些边缘类型作为特征，来预测图结构中缺失的边，该模型显著提高了计算效率，为大规模知识推理提供了一种有效的解决方案。在此基础上，Lao等进一步通过实验证明，基于约束、加权、随机遍历组合的软推理过程，可以更高效地预测知识库中的新知识，为此，进一步基于PRA提出了一种数据驱动的寻找路径的方法[67]，改进了PRA中的路径生成过程，将通过枚举生成的路径改进为仅生成可能对目标任务有信息增益的路径，利用实体之间所有路径的加权概率和得分对实体之间存在的关联关系进行度量。此外，实验结果证明，结合文本的语法模式和背景知识中的语义模式，路径约束的随机游走模型可以更有效地预测新的语义知识。

基于PRA的方法效率较高，且有着很好的可解释性，但是存在游走的过程中特征空间稀疏以及路径特征爆炸式增长的问题。Gardner等[68]则有针对性地将向量相似度考虑到随机游动的推理中，利用表层文本来减少固有特征的稀疏性，该模型仅允许在与语义上相一致的边上游动，其中语义的一致性由边类型的向量空间决定，减少了PRA特征空间的稀疏性。然而，此类推理方法大多对整个知识库进行推理，一方面，推理过程非常耗时，另一方面，全局结构信息粒度比较粗，因此Gardner等[69]在该方法的基础上进一步提出了一种更简单、高效的算法，结合细粒度的局部结构信息对知识图谱进行局部推理，称为子图特征提取（SFE）算法。当给定一些节点对时，该算法首先执行局部搜索来描述实体节点周围的子图，然后结合细粒度的局部信息，在这些局部子图上进行特征提取，得到每个实体对的特征向量，在此基础上进行知识推理，SFE算法不仅在推理性能上有了显著提升，时间复杂度也大大优于PRA算法。

Liu等[70]研究发现目前相关随机游走算法大多采用随机采样的方式提取关系路径特征，牺牲了知识图谱中语义信息的利用率，因此提出了双向语义假设和关系特异性推断假设，设计并实现了两层随机游走算法（TRWA）。TRWA将两种不同的特征建模方法结合起来，将知识图谱的拓扑结构细分为全局概览图和局部子图，分别进行特征提取，并对全局概览图和局部子图模块进行加权和合并，对结果进行推理。同时，为了避免纯粹的无引导随机游走算法寻找有用路径的低效，甚至引入噪声而误导推理的情况，Wei等[71]有针对性地提出了一种新的目标引导的推理算法，该算法在随机游走过程每一步都使用特定的推理目标作为引导，随机游走的过程中估计每个邻居节点的潜在可能性，从而实现这种目标引导机制。Wang等[72]提出了一种新的PRA多任务学习框架，称为耦合PRA（CPRA，coupling PRA）。CPRA使用多任务机制执行推理，由两个模块组成（关系聚类和关系耦合），前者用于自动发现高度相关的关系，后者用于耦合这些关系进行学习，通过耦合这些关系，模型能进一步学习关系的语义，提高推理的性能。

基于随机游走的知识推理方法可以获得预测结果具体的推理路径，提升结果的可解释性，但其中大多方法的路径选择过程是启发式遍历的，无目的随机游走挖掘有价值的推理路径效率较低，甚至会引入错误的推理规则。同时，在知识图谱稀疏、低连通的情况下，对路径特征的提取效率低且耗时。尽管一些学者提出使用启发式规则指导的随机游走策略取得一定的效果，但由于推理规则的多样性，这种方法很难取得较好的泛化性。

2.2.2 基于强化学习的知识推理

基于强化学习的方法进一步将知识推理中的多跳推理问题建模为一个序列化决策问题，知识推理中的每一条推理链代表一系列决策的过程，强化学习智能体在路径探索的过程中，通过反馈和交互的方式学习获得高奖励的路径寻找策略，从而对知识图谱中的多跳决策问题进行建模，实现知识推理。

Xiong等[73]提出了一种用于知识图谱推理的强化学习模型DeepPath，使用强化学习方法来解决知识图谱中的多跳推理问题。该模型利用强化学习的方法来评估采样路径，大大减少搜索空间。在路径推理的过程中，强化学习环境被建模为马尔可夫决策过程（MDP）。DeepPath模型结构如图6所示，通过设计一个策略函数来编码强化学习智能体的连续状态，智能体在向量空间环境下进行推理，在每一跳处对当前关系进行抽样，并扩展推理路径。奖励用于衡量智能体所发现路径的准确性、效率和多样性，从而监督每一跳的采样动作。

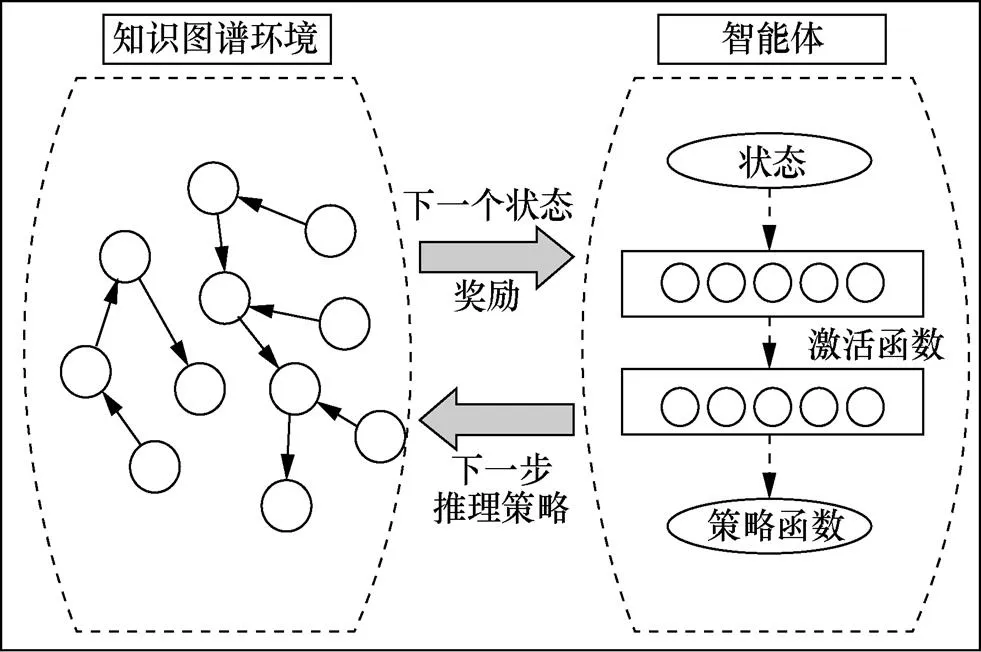
图6 DeepPath模型结构

Figure 6 Model structure of DeepPath

然而，DeepPath模型要求首先采样头部实体和尾部实体之间的所有路径，然后利用它们来评估尾部实体是否可以为正确答案，即（h, ?, t）的情况，无法处理尾部实体未知的情况，即（h, r, ?）的情况。Das等[74]提出了一种深度强化学习方法MINERVA，该学习方法根据输入查询来引导智能体，寻找预测路径，根据给定的头部实体和查询关系来获得正确的答案实体。MINERVA将环境建模为一个确定性的部分观察马尔可夫决策过程（POMDP）以减少行动空间。同时采用基于长短期记忆（LSTM）神经[75]网络的策略函数对经过节点的每个邻居进行表示，硬奖励0/1表示最后一步的采样实体是否为正确答案。实验结果进一步表明MINERVA可以学习相对较长的推理链，且推理的准确性较好。

以上强化学习方法均采用硬奖励机制来监督抽样过程，即抽样的实体为正确答案，奖励为1，否则为0。但是在不完整的知识图谱环境中，基于这种扩展路径策略的智能体大多只会得到稀疏的奖励，不足以指导复杂的强化学习模型进行学习。很多学者针对这一问题做出了探索，Lin等[76]有针对性地提出一种模型，其改进了MINERVA模型中硬奖励机制，提出了一种基于计算真实答案实体与最后一步采样实体之间相似性的软奖励方法RewardShaping，可以使智能体探索更多的路径集合，降低对虚假路径的敏感度。此外，受dropout技术的启发，该模型在训练过程中刻意忽略一些偶然行为，鼓励智能体选择不同路径，更有效地进行推理，缓解了过拟合的问题。Shen等[77]提出了一种基于值函数的强化学习方法M-walk，利用蒙特卡洛树搜索（MCTS）进行寻径，通过MCTS轨迹生成步骤和策略改进步骤迭代来细化策略函数，缓解奖励稀疏的问题。Godin等[78]进一步明确目前基于强化学习推理的方法中回馈奖励不明确的问题。通过引入三元奖励机制，对正确答案给予正奖励，对智能体采取规定步骤数无法达到候选实体或者一个错误的答案时，给予负奖励，对图谱中的信息无法回答的情况给予中性奖励，对智能体所获得的奖励进行量化，防止智能体对于错误路径的学习。

为进一步结合更多的辅助信息对强化学习的智能体进行指导，Lei等[79]提出了一种结合规则的知识图谱多跳推理模型RuleGuider，其利用基于符号的方法生成的高质量规则，为图谱上游走的智能体提供额外的规则奖励，实现RuleGuider在优化模型的性能同时，提升推理的可解释性。Xia等[80]提出的SparKGR对规则引导智能体探索的策略在稀疏的知识图谱环境中进一步进行探索，在判断下一步动作空间的过程中，融合了3种策略，分别是随机游走采样的方法、规则引导的方法以及利用智能体策略函数的方法，将3种方法对应的概率分布进行加权求和，综合判定智能体下一步的决策。

为了提高现有基于强化学习推理模型的鲁棒性，适应目前有噪声的推理环境，很多学者有针对性地做了不同的工作。Chen等[81]提出DIVA模型将知识图谱补全任务构建为一个统一的模型，使用变分推理方法来处理复杂推理，该模型将智能体寻找路径和推理预测作为一个整体，通过主动的协作和交互进行寻找路径，在这个过程中，路径被建模为隐变量，采用VAE 方法[82]对模型进行求解，路径推理模块可以从路径查找器中获得不同的推理路径，为结果提供不同的可解释依据。Li等[83]和Yu等[84]用强化学习和软规则联合的方法进行高效的图谱搜索，模型使用软规则的路径对知识图谱的规则进行补充，为路径推理中的关系增加不确定性，从而更好地进行模糊推理。Wang等[85]提出了一种基于注意力机制的深度强化学习（ADRL）框架，通过基于注意力机制的深度学习模型和强化学习的关系推理相结合的方法，提高了模型的效率和可解释性。Hildebrandt等[86]提出了一种基于动态生成对抗网络的知识图谱推理方法R2D2，R2D2通过将三元组的分类问题建模成两个强化学习智能体之间对抗博弈的任务，两个智能体分别寻找推理证据链，证明查询三元组正确或错误，并由一个判别器判定最终结果。这两个智能体可以被认为是稀疏的、对抗的特征生成器，通过训练为正例和反例分别提供可解释的依据。

总体来说，行为主义中知识图谱推理方法无须大量标注语料，仅需要一些推理目标即可得到泛化能力较强的模型，实现效率较高的推理。同时通过路径对推理结果的过程进行显性的回溯，在加快推理效率同时，提升了推理的可解释性。具体地，如表2所示，在可解释性的范围方面，行为主义中的可解释知识推理方法大多在知识图谱的图结构上进行多跳推理，推理出的路径针对具体的推理实例，提供了局部的可解释；在可解释的产生方式方面，所产生的解释是通过模型本身所产生的路径信息进行提供，所以解释性产生的方式是事前的可解释性；在可解释性的泛化性方面，基于随机游走的方法中，结合随机游走策略，通过图搜索算法进行知识推理，解释没有依靠模型以外的辅助方法，所以基于随机游走方法产生的解释与模型无关，而基于强化学习的方法虽然最后显式地给出推理路径，但其智能体的策略网络通常是基于LSTM等深度网络，在推理的过程中依赖LSTM等组件对路径历史信息进行嵌入，得出下一步的决策信息，所以基于强化学习方法产生的解释特定于具体模型；在可解释的下游场景适用性方面，适用于效率优先领域。

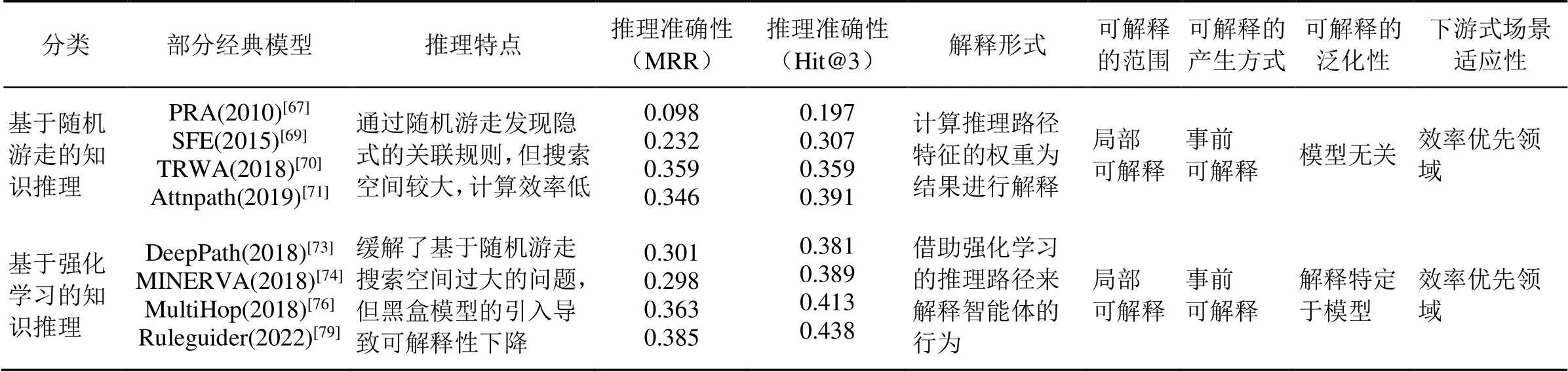
表2 行为主义中的可解释知识图谱推理方法

2.3 连接主义中的可解释知识图谱推理方法

从连接主义角度，知识图谱中的实体和关系可以通过表示学习方法嵌入低维向量空间，进行数值化的运算操作，进而实现知识推理。其核心是找到一种映射函数，将符号表示映射到向量空间进行数值表示，从而减少维数灾难，同时捕捉实体和关系之间的隐式关联，实现符号表示向量化的直接计算。

在语义的层面，很多浅层的表示模型在提升效率的同时，考虑建模不同的关系模式（如对称关系、逆反关系和组合关系）、逻辑操作（如与、或、非操作）和实体间的上下位层次关系，使模型具有推理部分语义结构的能力，因此，连接主义中的部分推理模型具有一定的可解释性。该类方法大体可以分为3种，分别是基于平移距离的模型、基于张量分解的模型和基于神经网络的模型，本文重点对方法的可解释性进行对比分析。

2.3.1 基于平移距离的知识推理

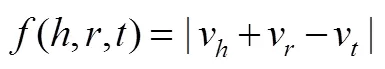
首先，TransE模型无法建模一对多和多对多的多映射关系。由于该模型基于在实数空间中转移思想的简单假设，在出现多映射关系时，即使语义相差很大，尾实体竞争向量空间中的同一个点，无法很好地建模此类多映射关系。Wang等[88]提出的TransH模型引入特定关系超平面，通过将实体和关系投影到特定关系超平面，从而对多映射关系有不同的表示，有效地处理一对多、多对多的关系。Lin等[89]提出的TransR模型则将原来的单个语义空间分离为实体空间和关系空间，通过线性变换将实体表示映射到对应的关系空间，提高了模型的表示能力，但参数量过大，模型收敛较慢。Ji等[90]提出的TransSparse模型在TransR工作的基础上，通过使用稀疏矩阵建模关系映射，缓解了TransR参数量过大的问题。

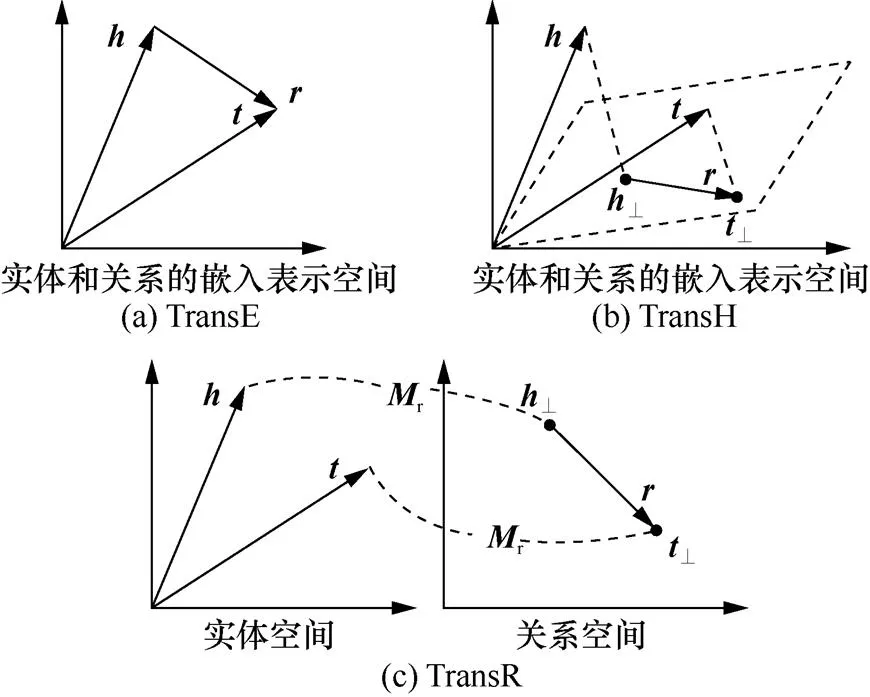
图7 部分平移距离模型示意

Figure 7 Simple illustrations of the translation distance model

其次，TransE模型无法建模所有的关系模式，特别是对称关系。该模型可以很好地建模反向、组合和非对称的关系模式，但由于实数空间的限制，在处理对称关系时有劣势。一些学者因此研究在复向量空间内进行更适合的实体和关系的嵌入表示。Sun等[91]提出的RotatE模型将实体表示为复数向量空间中的向量，将每个关系定义为在复矢量空间中从源实体到目标实体的旋转，这样相比实数空间的模型，可以更好地建模对称的关系。Zhang等[92]提出的QuatE模型通过旋转的思想进行建模对称关系，其采用四元向量来表示实体和关系，从而建模对称和非对称关系。Song等[93]提出的Rot-Pro模型则进一步对传递性的幂等关系实现了建模。Cao等[94]提出的DuelE模型进一步通过结合对偶四元数的方法将关系建模为一系列平移和旋转的组合操作，使对应嵌入推理更具有几何上的解释。

同时，TransE模型无法显式地建模实体的语义层级信息。Li等[95]证明，考虑实体的层次信息有助于缓解长尾实体的问题，进而利于知识推理，因此语义层次信息在建模过程中十分必要。Zhang等[96]提出的HAKE模型，通过极坐标方法，结合实体的模信息和相位信息，建模知识图谱中实体间语义层次关系的距离。Wang等[97]提出的HARotatE建模思想与HAKE相似，在RotatE的基础上通过定义模长，对实体间的层次信息进行建模。Hu等[98]则定义了实体的层级表示，将实体作为叶子节点，上层概念作为内部节点，构建有向无环图。Balazevic等[99]提出的MuRP模型则从表示空间的角度进行改进，将实体和关系映射到双曲几何空间，利用双曲几何中的庞加莱圆盘进行建模，有效地建模了实体的层次性质。

以上这类基于平移距离的模型大多是浅层的表示学习模型，由于参数量适中，运算操作简单高效，同时模型从表示空间、运算类型等方面进行建模，使对应的嵌入表示满足更多关系模式、层次关系或者可以进行更多的逻辑操作，因此对应的嵌入推理具有几何上的可解释性。

2.3.2 基于张量分解的知识推理

基于张量分解的模型又称为基于语义匹配的图嵌入方法。该类模型从文本语义的角度出发学习知识图谱中实体和关系的表示，如图8所示，该类模型首先通过将知识图谱建模为张量，然后通过张量分解来学习实体和关系的隐层表示，度量图谱中三元组潜在语义的合理性。该类模型最早由Nickel等[100]提出，提出的RESCAL模型将每个实体与向量关联来捕获其潜在语义，通过将得分函数定义为双线性函数捕获所有和实体间的成对交互作用，该模型能建模一对一、非对称关系和对称关系，但无法建模一对多关系，且参数规模较大。Yang等[101]提出的DisMult模型通过约束关系矩阵为对角矩阵，从而缓解参数量过大的问题，学习效率因此大幅度提升。Trouillon等[102]提出的ComplEx模型进一步扩展DistMult模型，通过引入复值嵌入来建模非对称和反向关系。Liu等[103]提出的ANALOGY模型则在RESCAL模型的基础上，假设关系的线性映射是相互可交换的，从而更好地建模实体和关系的类比属性。Balažević等[104]提出的TuckER模型则利用Tucker分解算法的性质，引入更加精简的张量分解方法对图谱张量进行分解，进一步提升了效率。相比基于平移距离的模型，基于张量分解的模型可以利用张量变换来表达知识图谱的关系变换，对于其中的语义也能进行合理的几何表示，因此可解释性较好。

2.3.3 基于神经网络的知识推理

基于神经网络的模型采用神经网络的方法学习知识图谱中三元组的语义关系。例如，NTN[105]、SME[106]、NAM[107]等模型均利用全连接神经网络来学习模型的得分函数，进而拟合图谱中的三元组的语义信息；ConvE[108]、ConvKB[109]和InteractE[110]等模型则利用卷积神经网络来学习模型的得分函数；Yao等[111]提出的KG-BERT模型则是利用BERT对语义关系进行建模；近些年有很多学者利用图神经网络以及图注意力机制对知识图谱进行表示学习建模[112]。虽然这种神经网络模型通过深层次的网络和海量的参数训练不断拟合知识图谱中三元组的语义信息，在推理准确率上取得了不错的效果，但由于深度学习网络的不可解释性，模型仅通过黑盒模型获取实体和关系的语义交互信息，相对于浅层表示学习模型，很难对知识图谱中实体和关系的层次性、关系模式和关系的多样性进行建模，所以可解释性较弱。

图8 部分基于张量分解的模型示意

Figure 8 Simple illustrations of the tensor factorization model

总体来看，连接主义中的知识推理方法可以进行高效的数值化运算完成推理任务，同时，很多浅层表示模型通过嵌入优化，表达语义层面的关系模式与逻辑操作，进而提升模型的可解释性。具体地，如表3所示，在可解释性的范围方面，连接主义中的可解释知识推理方法通过嵌入表示模型，对每一个实体和关系进行分布式表示，因而解释是面向具体的一个或一类实例，提供了局部的可解释；在可解释的产生方式方面，所产生的可解释性是通过提前设定的关系模式或者时间、实体类型等额外信息进行提供，解释需要模型以外的信息进行辅助，因此可解释的产生方式是事后可解释的。在可解释的泛化性方面，特定模型依赖于特定的假设或额外信息，所以解释特定于模型。同时，在连接主义的模型中，分布式表示的向量具体维度仍没有明确的解释，对用户来说，可解释性相对其他类型的方法仍较弱；在可解释的下游场景适用性方面，该类推理方法适用于效率优先领域。

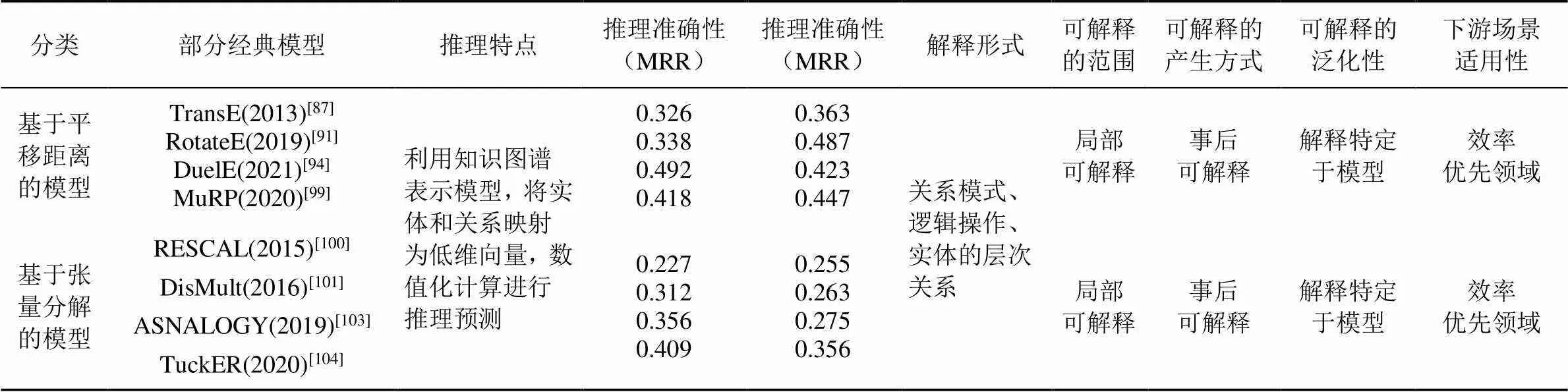
表3 连接主义中的可解释知识图谱推理方法

2.4 新型混合的可解释知识图谱推理方法

主流的挖掘隐式特征的嵌入学习模型（TransE[87]、RotatE[91]等），提升了模型的推理效率，但极大地影响了模型的可解释性。基于图遍历搜索的显式逻辑规则挖掘方法（AMIE+[52]、RDF2Rule[53]等）在提升推理过程可解释性的同时，效率方面有明显的欠缺。因此，通过结合两者的优势，利用符号推理在可解释性和准确性上的优势以及神经网络方法在鲁棒性与效率上的优势，进行混合推理[113]，可以一定程度解决传统规则方法的计算复杂度高等难题，同时提升神经网络方法的可解释性。根据推理的不同侧重点，可以将新型的混合推理方法分为符号规则增强神经网络的知识推理和神经网络增强符号规则的知识推理。

2.4.1 符号规则增强神经网络的知识推理

符号规则增强神经网络的知识推理，是指利用逻辑规则中的知识，推理新的实体和关系来进一步提升神经网络推理中的嵌入效率。模型不仅学习原始图谱中已经存在的三元组实例，同时学习通过逻辑规则推导出的一些置信度较高的三元组，使神经网络模型可以在更大的训练集上进行学习，在实现更高效推理预测的同时，间接提升神经网络模型推理的可解释性。

Guo等[114]提出的KALE模型通过一阶逻辑将三元组和规则统一起来，将其映射到一个统一的空间，并进行建模，通过联合模型将一阶谓词逻辑融入嵌入式表示。模型具体可分为3个部分：三元组建模、逻辑规则建模、联合学习。如图9所示，该模型利用TransE模型[87]对三元组进行建模，并使用t-norm模糊逻辑方法对规则进行建模，把三元组和规则建模为原子公式后，通过联合学习，最小化全局损失以学习同时满足三元组和规则的实体、关系的嵌入。为进一步将规则的一次性输入改进为迭代更新的方式，Guo等[115]在KALE的基础上提出了RUGE模型，RUGE模型没有像KALE模型那样直接将基本规则作为正实例处理，而是将由规则派生的三元组作为未标记三元组更新实体或关系的嵌入，RUGE根据当前的嵌入情况对每个未标记的三元组成立的概率进行预测，然后分别基于带标签和未带标签的三元组对实体和关系的嵌入进行更新，迭代地进行上述未标记三元组评分和嵌入更新过程，更新实体和关系的嵌入表示以进行推理。

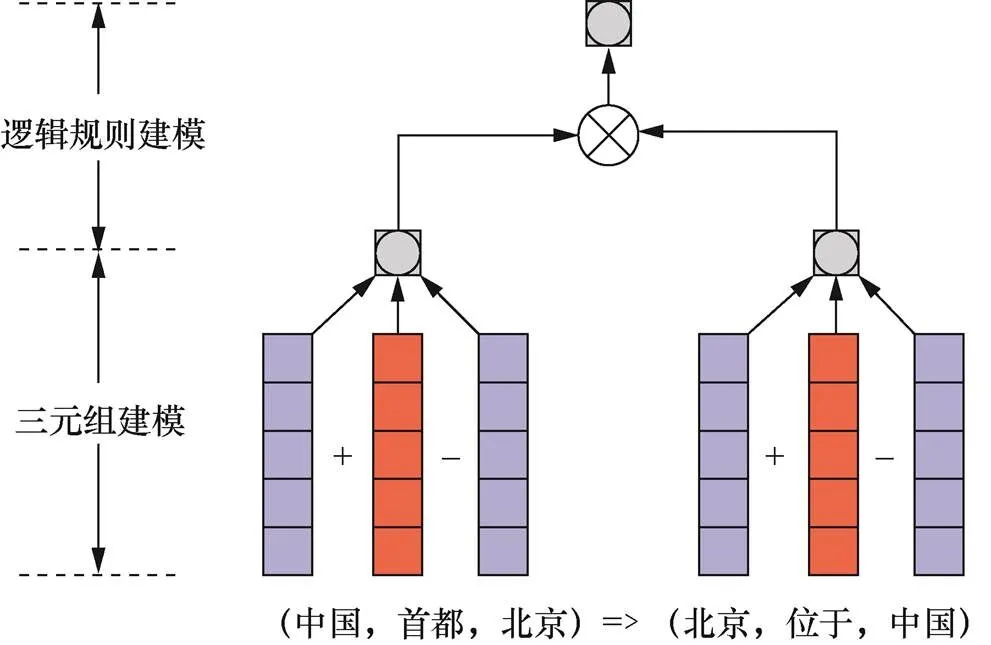
图9 KALE模型联合嵌入与规则推理示意

Figure 9 Illustration of joint embedding knowledge graph and logical rules in KALE

基于深度网络的规则归纳方法在推理的过程中存在参数难以解释的情况，因而可解释性通常较弱， Wang等[116]通过将三元组和基本逻辑规则都转换为一阶谓词逻辑来缓解这个问题，根据一阶逻辑中包含的实体和关系的嵌入情况，执行向量/矩阵运算，对一阶逻辑规则进行评分。表4说明了一阶逻辑格式的转换方式，表5说明了用数学表达式对一阶逻辑进行打分的方法。同一规则中包含的不同三元组，都可以直接在向量空间中进行操作，实现显式符号规则结构的发现和知识表达可解释性的增强。

表4 一阶逻辑格式的转换

表5 一阶逻辑的数学表达

在以上的方法中，规则的增强会促进更好的嵌入学习，但学习过程推理规则集合始终保持不变，即嵌入不会利于规则的归纳，不利于更好地挖掘新规则进行推理。不同于RUGE等模型构建方法，Zhang等[117]提出的IterE模型，通过迭代的方法基于更新的嵌入来推断新的规则，如图10所示，每一次迭代过程中分为3个步骤。首先，嵌入学习步骤学习知识图谱中实体和关系的向量表示；然后，基于实体和关系的嵌入表示对新的规则进行归纳，同时对规则挖掘的搜索过程进行剪枝；最后，公理推导则是将学习出的规则植入嵌入学习的过程，提升向量表示学习的效果。该迭代循环过程形成一个相互促进的过程，是一个演绎推理和归纳推理相互结合的框架。Cheng等[118]提出的UniKER则是设计一个统一的框架，融合了霍恩规则推理和嵌入表示学习，该框架以一个迭代式的方式将两者相互促进。一方面，霍恩规则推理推导出新的知识，帮助嵌入学习更好地表示；另一方面，嵌入学习可以帮助规则推理模块推导出更多的知识，两者相互迭代促进，使模型的学习和推理效果都得到提升。

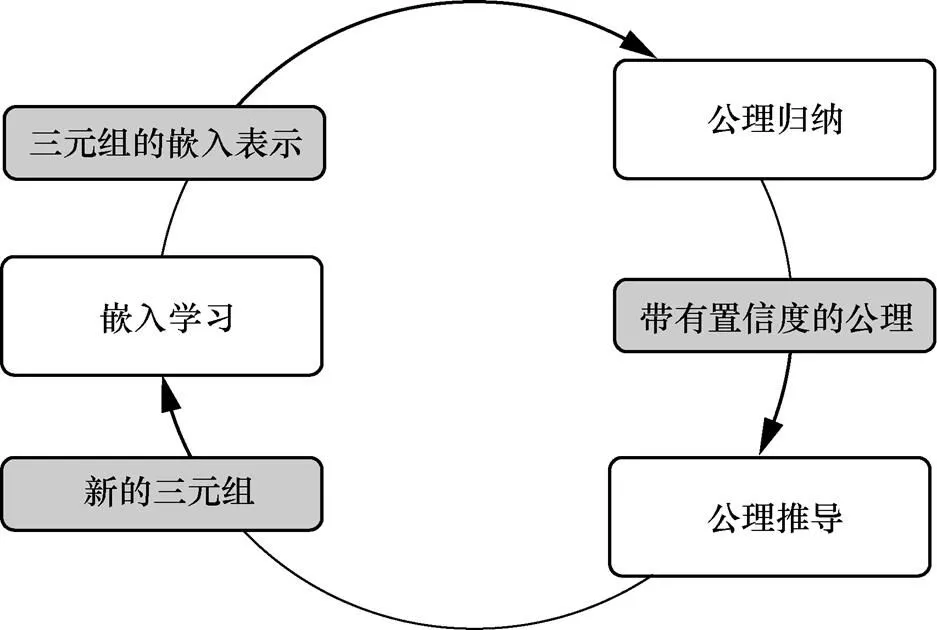
图10 IterE模型迭代训练示意

Figure 10 Overview of iterative training in IterE

融合关系路径和神经网络的知识推理技术最近引起了很多学者的关注。关系路径不仅在部分行为主义的推理方法中起着信息传播媒介的作用，同时关系路径可以看作符号的序列组合，结合神经网络的方法可以实现更加高效的推理，同时对推理的结果有显式的路径解释。Neelakantan等[119]提出了一种方法Path-RNN，Path-RNN使用PRA算法为每种关系类型找到不同的路径，利用循环神经网络将关系之间的连接进行表示，从而实现组合路径的多跳推理。Shen等[120]提出了隐式推理网络（IRN），在不使用任何附加信息的情况下，通过在向量空间中遍历知识图谱，将向量空间中的关系路径与模型联合进行训练，进而推断缺失的三元组。Das等[121]发现Path-RNN在预测时，只采用单一路径作为依据，且对每一个关系类型都要训练一个新的模型，变量数量多且无法共享。因此，他们提出了Single-Model模型，将所有递归神经网络的关系类型表示和组成矩阵进行共享，使相同的训练数据可以用较少的参数表示，显著地提高了基于循环神经网络的大规模图谱链接推理的可扩展性。Wang等[122]进一步为多跳推理问题引入了注意力机制。在找到实体间的所有可能推理路径后，根据注意力机制的打分值将这些路径的嵌入聚合为一个组合嵌入，并根据组合嵌入推断出实体之间的关系。Niu等[123]提出的RPJE模型则首先运用规则的先验知识实现符合路径的聚合规约，然后利用嵌入的方法对这些规约后的路径进行进一步的嵌入表示，在表示的损失计算中同时考虑路径生成的精度、规则生成的损失。

符号推理中基于马尔可夫逻辑网络的方法在理想的规则结构下可以实现高效的推理，但很难应对复杂的图结构，同时，图谱中缺失的三元组会影响该类模型规则推理的效果。Qu等[124]提出的PlogicNet模型通过结合马尔可夫逻辑网络和图谱嵌入技术来解决以上的问题，图谱嵌入技术可以高效推测缺失的三元组并通过随机梯度下降进行训练，而通过马尔可夫网络定义知识图谱中三元组的联合概率分布，为每一个逻辑规则赋予权重，通过变分EM算法来学习对应规则的权重，在该EM算法中，通过E-step推断了未观测三元组的似然值，而M-step则通过知识图谱嵌入模型中已有的三元组和模型推导出的三元组的似然估计来更新逻辑规则的权值。不同于PlogicNet中通过图谱嵌入技术对实体和关系进行向量化，Zhang等[125]提出的ExpressGNN模型通过结合马尔可夫逻辑网络和图神经网络的方法对实体和关系向量化，进而判定缺失三元组的正确或错误。而Vardhan等[126]提出的概率逻辑图注意力网络（PGAT，probabilistic logic graph attention network）模型则是利用图注意力机制，通过与一阶逻辑进行结合，优化了马尔可夫逻辑网络所定义的联合分布，进而对三元组的正误进行判定。以上介绍的3种模型的思想都是通过目前最新的一些嵌入手段对符号方法中的马尔可夫逻辑网络中三元组的联合分布进行优化，从而更加高效地在大规模的复杂图结构上进行推理。

2.4.2 神经网络增强符号规则的知识推理

符号推理的方法侧重于规则的学习，在逻辑推理上有着很好的表现，且有着很强的可解释性，但这类方法很难处理实体与关系的不确定性和数据的噪声问题，同时推理时搜索空间过大，导致推理效率低。神经网络增强符号规则的知识推理在逻辑规则推理的基础上，利用神经网络的方法的强学习和高泛化能力，解决数据的不确定性和歧义问题，提升数据处理的鲁棒性，缓解传统符号推理中规则学习搜索空间大的问题，进而提升规则学习和归纳推理的效率。该类方法的具体特点如表6所示。

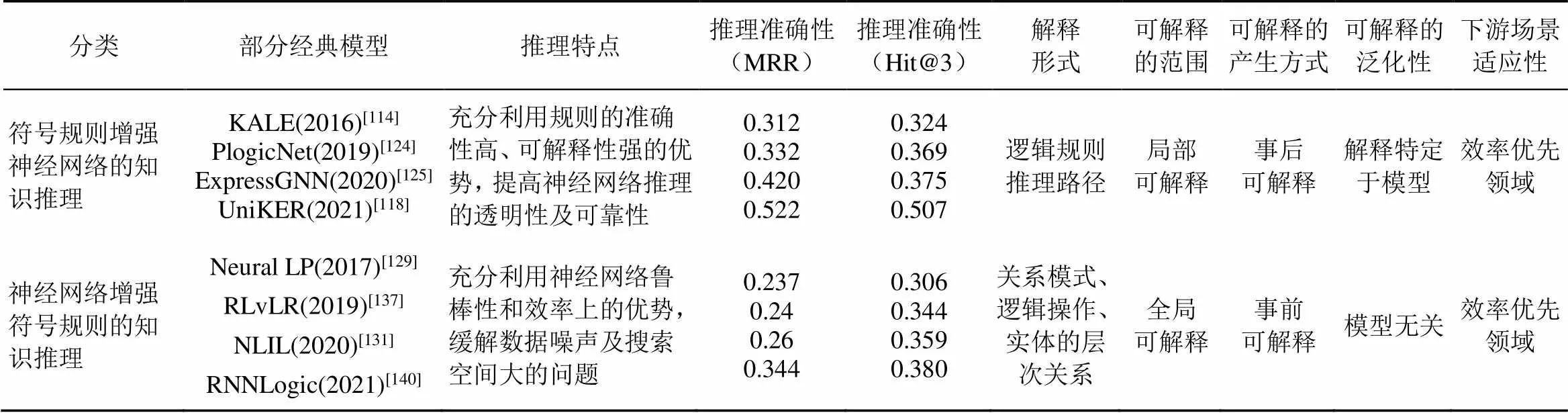
表6 混合的可解释知识图谱推理方法

为实现逻辑规则的高效数值化推理，Cohen等[127]将其建模为一个概率推理和学习的任务，并提出可微逻辑框架TensorLog，通过关系矩阵相乘来模拟知识推理和规则提取，实现了将规则推理编译成可微的操作序列，可微序列在推理的过程中可以进行更多数值化运算，实现更高效的推理。Evans等[128]提出的Differentable ILP模型则通过交叉熵损失函数对数值化转换的神经网络进行训练，实现将逻辑操作近似地通过可微操作进行替代。为进一步学习不同的规则结构，如图11所示。Yang等[129]提出的Neural LP模型加入了具有注意力机制和内存的神经控制器系统，通过马尔可夫逻辑网络进行神经网络的逻辑编程，将逻辑规则的结构和参数学习结合到一个端到端可微模型中，使模型能够同时学习参数和规则的结构。然而在Neural LP中，数值规则会导致稠密的矩阵操作，Wang等[130]提出的Num-Neural-LP模型对Neural LP进行扩展，通过动态规划和累积求和运算，实现对数值规则的快速学习，有效地表达用于数值比较的操作符。同时，Num-Neural-LP模型加入否定、聚合等操作符，使训练的规则形式更加丰富。为进一步提升表达和解释复杂规则的能力，Yan等[131]提出的NLIL模型利用分治策略，改进了一般用于解决逻辑规则归纳推理的框架。该模型将搜索空间分解为同一层次结构的3个子空间，每一个子空间都可以通过注意力机制进行推理，同时训练的过程分为规则生成和规则评估以维护规则的全局一致性，通过联合训练处理非链类规则。

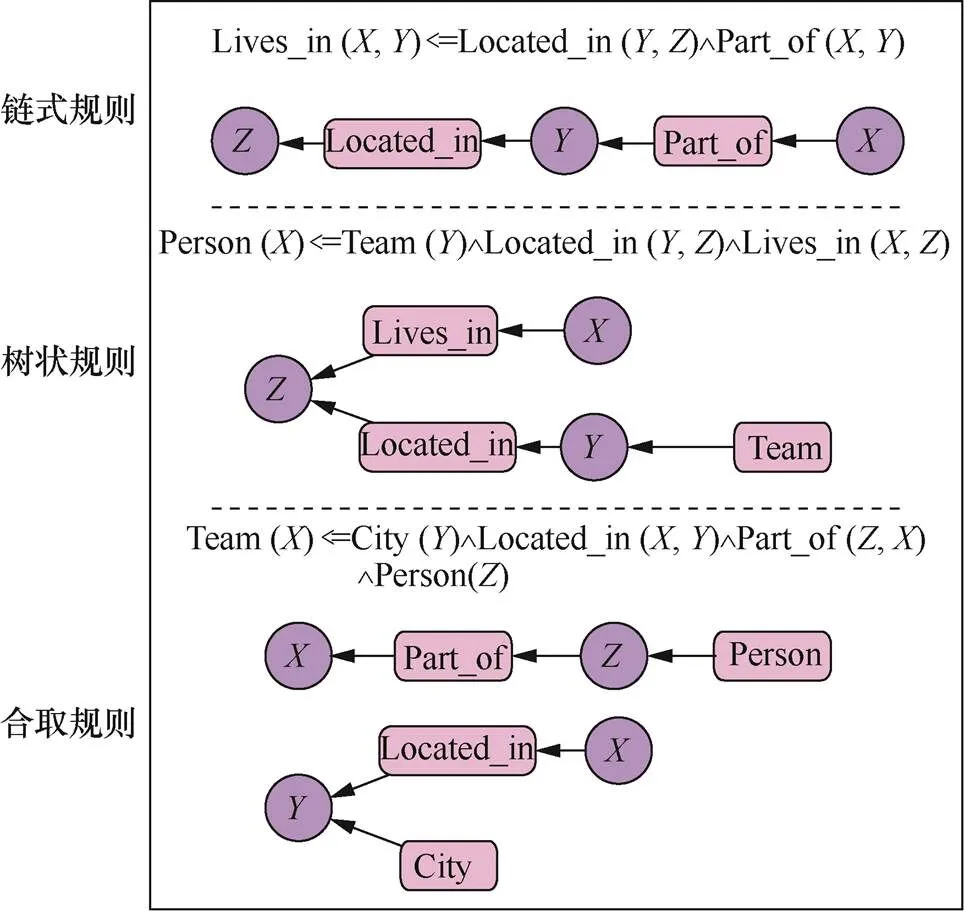
图11 不同类型逻辑规则推理结构

Figure 11 Different types of logical rule inference structures

最近兴起的图神经网络技术在混合推理中取得很好的效果[132]。Teru等[133]提出的归纳学习方法GraIL模型通过显式编码知识图谱中的规则，对抽取的子图运用图神经网络，并进行归纳式的关系推理。该模型假设对于两个需要被预测关系的目标节点之间，连通路径包含预测关系的信息，分3个步骤进行推理，如图12所示。首先对两个目标分别采样局部子图，然后对局部子图中的节点表示进行初始化，表示包含图的相关结构信息，最后利用图神经网络进行消息传递，利用得到的节点表示和整个局部图的表示进行计算打分，预测两个实体之间的关系。在GraIL的基础上，Du等[134]提出了CogKR模型，在每一步推理过程中通过策略函数将目标扩展多个实体，然后运用图神经网络模型，利用扩展子图对每个节点嵌入，CogKR再基于这些子图的嵌入预测答案。为使针对目标关系的推理更有针对性。Xu等[135]提出DPMPN模型，运用两个图神经网络模型进行整体和局部的混合推理。第一个图神经网络模型在整个知识图谱上进行输入不变的全局信息传递，可以为实体提供原始的语义表示。第二个图神经网络模型在与查询相关的子图上进行修剪后的消息传递，仅依赖于输入的语义，而与整个图分离，通过这种整体与局部的混合推理方式可以有针对性地实现更加高效的推理，且可以对推理的结果进行全局和局部的解释。

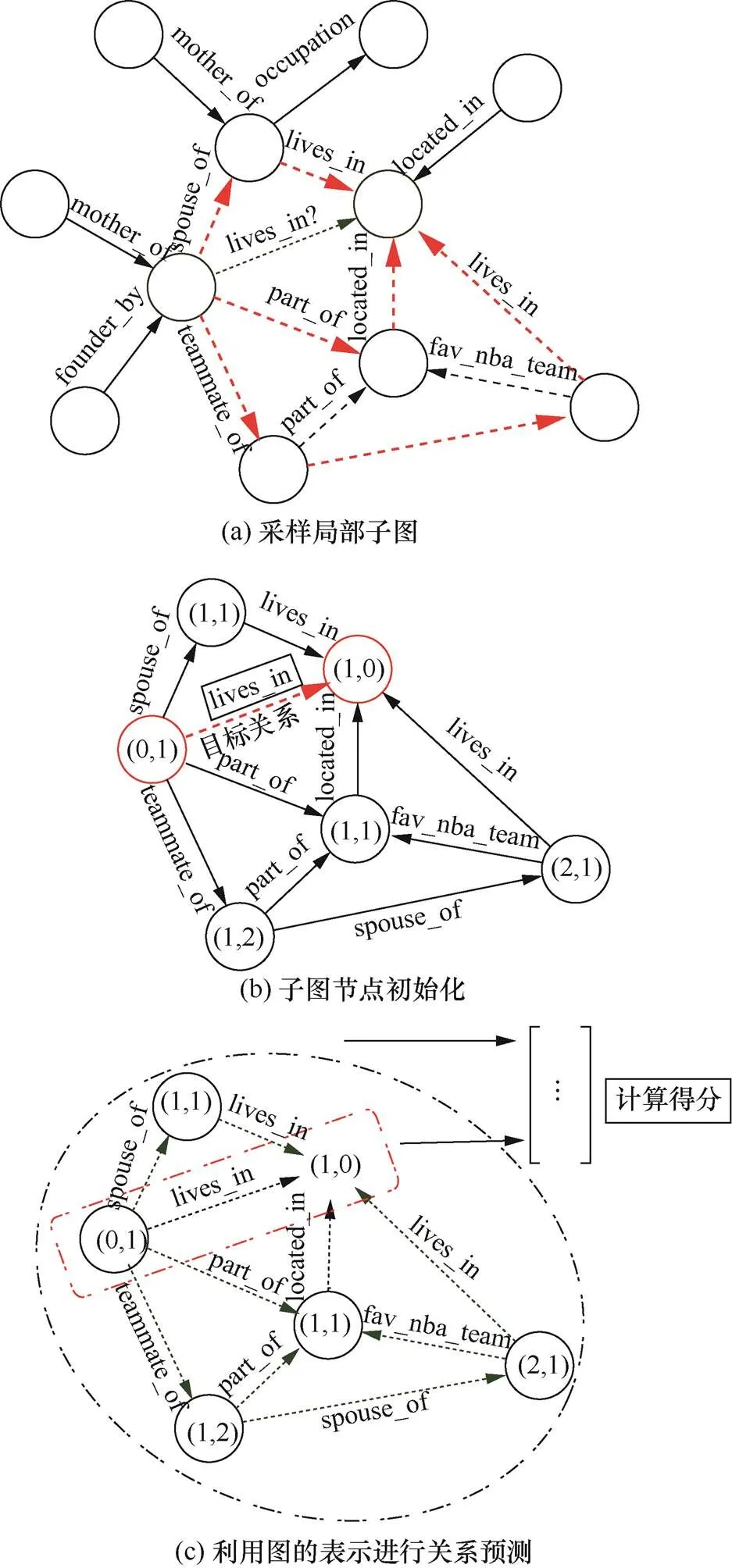
图12 GraIL模型[133]基于注意力机制的可解释推理

Figure 12 Explainable reasoning based on attention mechanism in GraIL model[133]

逻辑规则可以为模型预测提供较好的可解释性依据，但在传统归纳学习方法中，规则的搜索空间通常过大，且无法应对噪声或者是有歧义的数据，鲁棒性比较差，很多归纳规则模型通常与神经网络相结合。Ho等[136]提出的RuLES模型则利用额外的文本信息训练嵌入模型，通过学习到的模型来衡量所学习到逻辑规则的质量。Omran等[137]提出的RLvLR模型通过在知识图谱中运用合适的采样策略和表示学习方法，更快地学习到高质量的规则，该模型首先对与目标谓词相关的子图进行采样，然后利用知识图谱嵌入模型RESCAL[100]生成实体和关系的子图嵌入，最后利用基于嵌入的评分函数对规则的搜索进行引导和修剪，并根据AMIE[52]中定义的度量覆盖度和置信度对候选规则进行评价。Dong等[138]则提出一个新型的神经符号体系（NLM，neural logic machine）结构，用于一阶逻辑归纳学习和推理，缓解搜索空间大的问题。NLM利用神经网络作为函数近似器，逻辑编程作为具有属性、关系和谓词等对象的符号处理器，使整个逻辑编程推理过程计算可微，实现模型端到端的训练。Pan等[139]提出了一种基于关系路径对比的规则归纳推理模型RPC-IR，该模型对局部子图结构进行推理，通过构建正、负关系路径的自监督学习方法，提取每一个子图的关系路径并引入对比学习以获取自监督信息，结合监督和自监督信息联合训练策略来训练推理模型。Qu等[140]提出的RNNlogic模型从隐变量的角度提出了一种新的推理方法，该模型将逻辑规则视为隐变量，同时用归纳出的逻辑规则训练规则生成器和推理预测器，通过EM算法对模型参数进行优化，有效地解决了搜索空间过大的问题，同时提高推理预测结果的准确率。

3 结束语

随着人工智能技术的广泛应用，人工智能的可解释性受到越来越多的关注。在目前流行的深度学习模型中，复杂的处理机制与大量的参数使人类很难追溯与理解其推理过程，导致这种端到端的黑箱学习方法可解释性较差。知识图谱作为知识的一种语义化和结构化的表达方式，以人类可理解的表达形式进行知识推理，通过推理路径、逻辑规则等辅助手段，结合节点周围的实体信息，进行显式的可解释知识图谱推理，为实现可解释人工智能提供了一种解决方案，在信息检索、信息安全、网络空间安全等领域都有广泛的应用前景，引发了广泛的关注。

3.1 可解释的知识图谱推理方法总结

本文概述了可解释人工智能及知识推理的相关概念，从经典的人工智能三大研究范式的角度出发，总结和分析了可解释的知识推理方法。无论是以符号主义中的本体推理和规则推理方法为代表的具有全局模型可解释性的模型，还是通过将推理过程显式地进行学习（具体表现为证明、关系路径和逻辑规则等方式），从而为推理预测提供可解释性依据的具有事后过程可解释性的模型，都一定程度增强了人们对推理结果的理解，同时实现对错误预测原因的辅助挖掘。

如表7所示，本文对所介绍的知识图谱推理方法及特点进行相关的总结与对比分析。这些推理方法根据推理目的不同，在推理准确性和可解释性方面各有侧重，所适用的推理应用场景也因此不同。符号主义中的知识推理模型有着很好的可解释性，推理准确、迁移性好。然而，离散的符号表示方法通常不足以描述数据之间所有内在关系，造成规则学习的搜索空间太大、效率较低，且对数据中出现的噪声鲁棒性较差（如AMIE+[52]、RDF2Rule[53]），因此这种推理方法适用于数据库知识结构规整，要求推理精度及可解释程度较高的推理场景，如医疗和信息安全等要求可靠性优先的领域。在行为主义中的知识推理模型中，以强化学习为代表，通过反馈和交互训练智能体，鼓励获得更大的奖励，实现了较高的推理效率，同时得到具体的推理路径，可解释性虽然相较于逻辑规则有所降低，但得到了具体的推理步骤，具有过程的可解释性（如DeepPath[73]、MINERVA[74]），因此这种推理方法更适用针对序列决策问题的多跳知识推理场景，如网络安全领域的攻击路径推理图谱，推理效率和可解释性均有较大的优势。在连接主义中的知识推理模型中，通过数值化运算实现的模糊推理，加快了推理的速度，增强了模型的鲁棒性和推理效率，但不能为预测结果提供显式的推理过程说明，对模型的可解释性造成了很大影响（如TransE[87]、RotatE[91]），凭借其效率和鲁棒性的优势，这种推理方法适用在低风险但效率要求较高的效率优先领域，如电影推荐系统与问答系统等。在新型混合的推理模型中，结合符号推理在可解释性上的优势和神经网络推理在鲁棒性与效率上的优势进行的新型混合推理，无论是利用逻辑规则生成更多实例，辅助高质量嵌入学习，还是通过神经网络模型辅助解决数据的歧义和不确定性，帮助归纳出更多的显式逻辑规则，推理的可解释性和效率都得到了提升（如IterE[117]、RNNLogic[140]），这种推理方法则更加需要结合系统及应用需求，根据目标任务要求的效率或可解释性等指标的不同，动态调整对应神经网络推理方法和符号推理方法的侧重点，有针对性地进行推理。

表7 可解释的知识推理方法及特点

注：由于符号主义中基于本体的知识推理为概念层的推理，推理准确率不以比较。

3.2 有待进一步解决的问题和挑战

虽然目前可解释的知识图谱推理方法在不同的研究范式下都取得了一定进展，但该领域仍处于发展时期，各类方法在推理的准确性和推理过程的可解释性上很难达到平衡，需要在理论和实际应用中进一步完善，在未来的研究中，可解释的知识推理还面临很多新的挑战，主要有以下4个方面值得探索。

1) 结合常识知识的可解释推理。常识推理即利用人类对世界和行为基本理解的常识认知进行推理。结合目前人类在深度学习方面的进展，表征并融入常识知识于推理模型，从而创造更加贴近人类思维习惯的模型，将从本质上增加模型行为的透明度，帮助人们获得更具可解释性的结果。

2) 考虑复杂推理模式的可解释知识推理。在知识逻辑推理中，推理的规则主要遵循传递性约束，即链状的推理，表达能力有限。但是现实生活中所要面临的要素更加复杂，需要支持更复杂推理模式，自适应地挖掘更多样、有效的推理结构，如实现对树状或网状等结构的逻辑规则推理[130]，同时保证挖掘规则的可靠性和可解释性，辅助更多样的决策。

3) 多模态的可解释知识推理。解释方法大多通过推理文本中的逻辑规则或路径从而实现可解释性，但随着移动通信技术的快速发展，如何有效地利用语音、图片等多模态信息进行解释成为一个具有挑战性的问题[141]。多模态信息显示出其对知识图谱进行可解释推理的潜力，可以通过图像、声音等多种模态对于推理的过程与结果进行语义增强的解释。

4) 可解释性的量化度量指标。对于可解释性的优劣并不存在非常成熟的、广为接受的量化标准。大多数已有的方法是主观度量，因而只能定性分析，无法对可解释模型的性能进行量化。这就造成用户无法非常准确地判断解释方法的优劣[142]，所以需要进一步研究科学合理的可解释的评测指标，对解释方法进行量化评价，模型得到反馈并进行相关优化，从而更好地指导系统的决策。

[1] RISSOLA E A, BAHRAINIAN S A, CRESTANI F. Personality recognition in conversations using capsule neural networks[C]//Proceedings of the Int Conf on Web Intelligence. 2019: 180-187.

[2] SADAK F, SAADAT M, HAJIYAVAND A M. Real-time deep learning-based image recognition for applications in automated positioning and injection of biological cells[J]. Computers in Biology and Medicine, 2020, 125(10): 103976.

[3] VALMADRE J, BERTINETTO L, HENRIQUES J, et al. End-to-end representation learning for correlation filter based tracking[C]//Proceedings of the IEEE Conf on Computer Vision and Pattern Recognition. 2017: 2805-2813.

[4] MILLEN J. A survey of methods for explaining black box models[J]. Computing Reviews, 2019, 60(4):175-176.

[5] DOSHI-VELEZ F, KIM B. Towards a rigorous science of interpretable machine learning[J]. arXiv preprint arXiv: 1702.08608, 2017.

[6] ZHANG YU, TINO P, LEONARDIS A, et al. A survey on neural network interpretability[J]. arXiv preprint arXiv: 2012.14261, 2021.

[7] 成科扬, 王宁, 师文喜, 等. 深度学习可解释性研究进展[J]. 计算机研究与发展, 2020, 57(6): 1208-1217.

CHENG K Y, WANG N, SHI W X, et al. Research advances in the interpretability of deep learning[J]. Journal of Computer Research and Development, 2020, 57(6): 1208-1217.

[8] GAWEHN E, HISS J A, SCHNEIDER G. Deep learning in drug discovery[J]. Molecular Informatics, 2016, 35(1):3-14.

[9] 方滨兴. 定义网络空间安全[J]. 网络与信息安全学报, 2018, 4(1): 1-5.

FANG B X. Define cyberspace security[J]. Chinese Journal of Network and Information Security, 2018, 4(1): 1-5.

[10] HOFMAN J M, SHARMA A, WATTS D J. Prediction and explanation in social systems[J]. Science, 2017, 355(6324):486-488.

[11] 胡浩, 刘玉岭, 张玉臣, 等. 基于攻击图的网络安全度量研究综述[J]. 网络与信息安全学报, 2018, 4(9): 1-16.

HUH, LIUYL, ZHANGYC, et al. Survey of attack graph based network security metric[J]. Chinese Journal of Network and Information Security, 2018, 4(9): 1-16.

[12] CHEN X, JIA S, XIANG Y. A review: knowledge reasoning over knowledge graph[J]. Expert Systems with Application, 2020, 141(3):1-21.

[13] AMIT S. Introducing the knowledge graph[R]. America: Official Blog of Google, 2012.

[14] DAVID G, MARK S, JAESIK C, et al. XAI-Explainable artificial intelligence [J]. Science Robotics, 2019,4(37):7120.

[15] 官赛萍, 靳小龙, 贾岩涛, 等. 面向知识图谱的知识推理研究进展[J]. 软件学报, 2018, 29(10): 2966-2994.

GUAN S P, JIN X L, JIA Y T, et al. Knowledge reasoning over knowledge graph: a survey[J]. Journal of Software, 2018, 29(10): 2966-2994.

[16] WANG Q, MAO Z, WANG B, et al. Knowledge graph embedding: a survey of approaches and applications[J]. IEEE Transactions onKnowledge and Data Engineering, 2017, 29(12): 2724-2743.

[17] ARORA S. A Survey on graph neural networks for knowledge graph completion[J]. arXiv preprint arXiv:2007.12374, 2020.

[18] LIPTON Z C. The mythos of model interpretability[J]. Communications of the ACM, 2016, 61(10):31-57

[19] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. Advances in Neural Information Processing Systems, 2012, 25(2):84-90.

[20] PAPERNOT N, MCDANIEL P, JHA S, et al. The limitations of deep learning in adversarial settings[C]//Proceedings of 2016 IEEE European Symp on Security and Privacy. 2016: 372-387.

[21] SUCHANEK F M, KASNECI G, WEIKUM G. Yago: a core of semantic knowledge[C]//Proceedings of the 16th Int Conf on World Wide Web. 2007:697-706

[22] AUER S, BIZER C, KOBILAROV G, et al. Dbpedia: a nucleus for a Web of open data[M]//Proceedings of the Semantic Web. Berlin: Springer, 2007.

[23] BOLLACKER K, EVANS C, PARITOSH P, et al. Freebase: a collaboratively created graph database for structuring human knowledge[C]//Proceedings of the 2008 ACM SIGMOD Int Conf on Management of Data. 2008:1247-1250.

[24] HU S, ZOU L, YU J X, et al. Answering natural language questions by subgraph matching over knowledge graphs[J]. IEEE Trans on Knowledge and Data Engineering, 2017, 30(5):824-837.

[25] PALUMBO E, RIZZO G, TRONCY R. Entity2rec: learning user-item relatedness from knowledge graphs for top-n item recommendation[C]//Proceedings of the 7th ACM Conf on Recommender Systems. 2017:32-36.

[26] 宋蕾, 马春光, 段广晗. 机器学习安全及隐私保护研究进展[J]. 网络与信息安全学报, 2018, 4(8): 1-11.

SONGL, MACG, DUANGH. Machine learning security and privacy: a survey[J]. Chinese Journal of Network and Information Security, 2018, 4(8): 1-11.

[27] 任奎, 孟泉润, 闫守琨, 等. 人工智能模型数据泄露的攻击与防御研究综述[J]. 网络与信息安全学报, 2021, 7(1): 1-10.

RENK, MENGQR, YANSK, et al. Survey of artificial intelligence data security and privacy protection[J]. Chinese Journal of Network and Information Security, 2021, 7(1): 1-10.

[28] BADER S, GRANGEL-GONZALEZ, NANJAPPA P, et al. A knowledge graph for industry 4.0[C]//Proceedings of the 2020 European Semantic Web Conf. 2020: 465-480.

[29] ISA B, MSBC D. Open-CyKG: an open cyber threat intelligence knowledge graph[J]. Knowledge-Based Systems, 2021, 233: 107524.

[30] 刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247-261.

LIU Z Y, SUN M S, LIN Y K, et al. Knowledge representation learning: a review[J]. Journal of Computer Research and Development, 2016, 53(2): 247-261.

[31] LECUE, FREDDY. On the role of knowledge graphs in explainable AI[J]. Semantic Web, 2020, 11(1):41-51.

[32] 刘峤,李杨,段宏,等. 知识图谱构建技术综述[J]. 计算机研究与发展, 2016, 53(3): 582-600.

LIU Q, LI Y, DUAN H, et al. Knowledge graph construction techniques[J]. Journal of Computer Research and Development, 2016, 53(3): 582-600.

[33] 刘潇,刘书洋,庄韫恺,等.强化学习可解释性基础问题探索和方法综述[J]. 软件学报, 2021.

LIU X, LIU S Y, ZHUANG W K, et al. Explainable reinforcement learning: basic problems exploration and asurvey[J]. Journal of Software, 2021.

[34] EHRLINGER L, WOLFRAM W. Towards a definition of knowledge graphs[C]//Proceedings of the Posters and Demos Track of 12th International Conference on Semantic Systems - SEMANTiCS2016 and 1st International Workshop on Semantic Change & Evolving Semantics (SuCCESS16). 2016.

[35] CHEN X, CHEN H J, ZHANG N Y, et al. OWL reasoning over big biomedical data[C]//Proceedings of the 2013 IEEE Int Conf on Big Data. 2013: 29-36.

[36] ZHANG D H, YUAN Z X, LIU H, et al. Learn to walk with dual agents for knowledge graph reasoning[C]//Proceedings of the 2022 AAAI Conf on Artificial Intelligence. 2022: 5932-5941.

[37] ZOU Y, FININ T, CHEN H. F-OWL: an inference engine for semantic Web[C]//Proceedings of the Int Conf on Formal Approaches to Agent-based Systems. 2004:238-248.

[38] SIRIN E, PARSIA B, GRAU B C, et al. Pellet: a practical OWL DL reasoner[J]. Journal of Web Semantics, 2007, 5(2):51-53.

[39] WEI Y Z, LUO J, XIE HY. KGRL: an OWL2 RL reasoning system for large scale knowledge graph[C]//Proceedings of the 12th Int Conf on Semantics, Knowledge and Grids. 2016:83-89.

[40] ZHOU J, MA L, LIU Q, et al. Minerva: a scalable OWL ontology storage and inference system[C]//Proceedings of the Asian Conf on the Semantic Web. 2006:429-443.

[41] SOMA R, PRASANNA V K. Parallel inferencing for OWL knowledge bases[C]//Proceedings of the 37th Int Conf on Parallel Processing. 2008:75-82.

[42] MARX M, KRÖTZSCH M, THOST V. Logic on mars: ontologies for generalised property graphs[C]//Proceedings of the 26th Int Joint Conf on Artiﬁcial Intelligence. 2017:118-1194.

[43] CHEN Y, GOLDBERG S, WANG D Z, et al. Ontological pathfinding: mining first-order knowledge from large knowledge bases[C]//Proceedings of the 2016 Int Conf on Management of Data. 2016: 835-846.

[44] HAO J H, CHEN M H, YU W C, et al. Universal representation learning of knowledge bases by jointly embedding instances and ontological concepts[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD '19). 2019: 1709-1719.

[45] KULMANOV M, LIU-WEI W, YAN Y, et al. El Embeddings: geometric construction of models for the description logic el++[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI-19). 2019:6103-6109.

[46] DENG S, ZHANG N, LI L, et al. Ontoed: low-resource event detection with ontology embedding[J]. arXiv preprint arXiv:2105.10922, 2021.

[47] SCHOENMACKERS S, ETZIONI O, WELD D S, et al. Learning ﬁrst-order horn clauses from Web text[C]//Proceedings of the 2010 Conf on Empirical Methods in Natural Language Processing. 2010:1088-1098.

[48] LANDWEHR N, KERSTING K, RAEDT L D. Integrating naive Bayes and FOIl[J]. Journal of Machine Learning Research, 2007, 8(5):481-507.

[49] LANDWEHR N, PASSERINI A, RAEDT L D, et al. Fast learning of relational kernels[J]. Machine Learning, 2010, 78(3):305-342.

[50] NAKASHOLE N, SOZIO M, SUCHANEK F M, et al. Query-time reasoning in uncertain RDF knowledge bases with soft and hard rules[J]. VLDS, 2012, 884(6):15-20.

[51] GALÁRRAGA L, TELIOUDI C, HOSE K, et al. Fast rule mining in ontological knowledge bases with AMIE+[J]. The Int Journal on Very Large Data Bases, 2015, 24(6):707-730.

[52] GALÁRRAGA L, TELIOUDI C, HOSE K, et al. Amie: association rule mining under incomplete evidence in ontological knowledge bases[C]//Proceedings of the 22nd Int Conf on World Wide Web. 2013:413-422.

[53] WANG Z C, LI J Z. RDF2Rules: learning rules from RDF knowledge bases by mining frequent predicate cycles[J]. arXiv preprint arXiv: 1512.07734, 2015.

[54] KOK S, DOMINGOS P. Learning the structure of Markov logic networks[C]//Proceedings of the 22nd Int Conf on Machine Learning. 2005: 441-448.

[55] RICHARDSON M, DOMINGOS P. Markov logic networks[J]. Machine Learning, 2006, 62(1-2): 107-136.

[56] ONDREJ K, JESSE D. Markov logic networks for knowledge base completion: a theoretical analysis under the MCAR assumption[C]//Proceedings of the 35th Uncertainty in Artificial Intelligence Conf. 2020: 1138-1148.

[57] DE-RAEDT L, KIMMIG A, TOIVONEN H. A probabilistic prolog and its application in link discovery[C]//Proceedings of the 20th Int Joint Conf on Artiﬁcal Intelligence. 2007:2462-2467.

[58] CUSSENS J. Parameter estimation in stochastic logic programs[J]. Machine Learn, 2001, 44 (3):245-271.

[59] WANG W Y, MAZAITIS K, COHEN W W. Programming with personalized pagerank: a locally groundable ﬁrst-order probabilistic logic[C]//Proceedings of the 22nd ACM Int Conf on Information & Knowledge Management. 2013:2129-2138.

[60] HAVELIWALA T H. Topic-sensitive PageRank: a context-sensitive ranking algorithm for Web search[J]. IEEE Trans on Knowledge and Data Engineering, 2003, 15(4):784-796.

[61] KIMMIG A, BACH S H, BROECHELER M, et al. A short introduction to probabilistic soft logic[C]//Proceedings of the NIPS Workshop on Probabilistic Programming: Foundations and Applications. 2012:1-4.

[62] PUJARA J, MIAO H, GETOOR L, et al. Ontology-aware partitioning for knowledge graph identiﬁcation[C]//Proceedings the Workshop on Automated Knowledge Base Construction. 2013:19-24

[63] BACH S H, BROECHELER M, HUANG B, et al. Hinge-loss markov random fields and probabilistic soft logic[J]. Computer Science, 2017, 18(1):1-67.

[64] MEILICKE C, CHEKOL M W, FINK M, et al. Reinforced anytime bottom up rule learning for knowledge graph completion[J]. arXiv preprint, arXiv:2004.04412, 2020.

[65] PEDRESCHI D, GIANNOTTI F, GUIDOTTI R, et al. Meaningful explanations of black box ai decision systems[C]//Proceedings of the AAAI Conf on Artificial Intelligence. 2019.

[66] LAO N, COHEN W. Relational retrieval using a combination of path-constrained random walks[J]. Machine Learning, 2010, 81(1): 53-67.

[67] LAO N, MITCHELL T, COHEN W. Random walk inference and learning in a large scale knowledge base[C]//Proceedings of the 2011 Conf on Empirical Methods in Natural Language Processing. 2011:27-31.

[68] GARDNER M, TALUKDAR P, KRISHNAMURTHY J, et al. Incorporating vector space similarity in random walk inference over knowledge bases[C]//Proceedings of the 2014 Conf on Empirical Methods in Natural Language Processing. 2014:397-406.

[69] GARDNER M, MITCHELL T. Eﬃcient and expressive knowledge base completion using subgraph feature extraction[C]//Proceedings of the 2015 Conf on Empirical Methods in Natural Language Processing. 2015:1488-1498

[70] LIU Q, HAN M, JIANG L, et al. Two-tier random walk based relational inference algorithm[J]. Chineses Journal of Computers, 2017, 40(6):1275-1290.

[71] WEI Z, ZHAO J, LIU K. Mining inference formulas by goal-directed random walks[C]//Proceedings of the 2016 Conf on Empirical Methods in Natural Language Processing. 2016:1379-1388.

[72] WANG Q, LIU J, LUO Y F, et al. Knowledge base completion via coupled path ranking[C]//Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics. 2016:1308-1318.

[73] XIONG W H, HONG T, WANG W Y. DeepPath: a reinforcement learning method for knowledge graph reasoning[C]//Proceedings of the 2017 Conf on Empirical Methods in Natural Language Processing. 2017: 564-573.

[74] DAS R, DHULIAWALA S, ZAHEER M, et al. Go for a walk and arrive at the answer: reasoning over paths in knowledge bases using reinforcement learning[C]//Proceedings of the 6th Int Conf on Learning Representations. 2018.

[75] GREFF K, SRIVASTAVA R K, KOUTNÍK J, et al. LSTM: a search space odyssey[J]. IEEE Trans on Neural Networks & Learning Systems, 2016, 28(10):2222-2232.

[76] LIN X V, SOCHER R, XIONG C M. Multi- hop knowledge graph reasoning with reward shaping[C]//Proceedings of the 2018 Conf on Empirical Methods in Natural Language Processing. 2018: 3243-3253.

[77] SHEN Y, CHEN J, HUANG P S, et al. M-Walk: learning to walk over graphs using monte carlo tree search[C]//Proceedings of the 32nd Int Conf on Neural Information Processing Systems. 2018: 6786-6797.

[78] GODIN F, KUMAR A, MITTAL A. Using ternary rewards to reason over knowledge graphs with deep reinforcement learning[C]//Proceedings of the 2019 Conf and Workshop on Neural Information Processing Systems. 2019:846-852.

[79] LEI D R, JIANG G G, GU X T, et al. Learning collaborative agents with rule guidance for knowledge graph reasoning[C]//Proceedings of the 2020 Conf on Empirical Methods in Natural Language Processing.2020:8541-8547.

[80] XIA Y, LAN M J, LUO J Y, et al. Iterative rule-guided reasoning over sparse knowledge graphs with deep reinforcement learning [C]//Information Processing & Management. 2022:103040.

[81] CHEN W H, XIONG W H, YAN X F, et al. Variational knowledge graph reasoning[C]//Proceedings of the 2018 Conf of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. 2018: 1823-1832.

[82] KINGMA D P, WELLING M. Auto-encoding variational Bayes[C]//Proceedings of the 2nd Int Conf on Learning Representations. 2014: 1-14.

[83] LI Z X, JINX L, GUAN S P, et al. Path reasoning over knowledge graph: a multi-agent and reinforcement learning based method[C]//Proceedings of the 2018 IEEE Int Conf on Data Mining Workshops. 2018:929-936.

[84] YU W T, MA X G, BAI L Y, et al. Path-based knowledge graph completion combining reinforcement learning with soft rules[C]//Proceedings of the Int Conf on Natural Computation, Fuzzy Systems and Knowledge Discovery. 2019:139-146.

[85] WANG Q, HAO Y S, CAO J. ADRL: an attention-based deep reinforcement learning framework for knowledge graph reasoning[J]. Knowledge-Based Systems, 2020, 197(7):105910.

[86] HILDEBRANDT M, SERNA J A Q, MA Y P, et al. Reasoning on knowledge graphs with debate dynamics[C]//Proceedings of the 34th AAAI Conf on Artiﬁcial Intelligence. 2020:4123-4131.

[87] BORDES A, USUNIER N, GARCIADURAN A, et al. Translating embeddings for modeling multi-relational data[C]//Proceedings of the 26th Int Conf on Neural Information Processing Systems. 2013: 2787-2795.

[88] WANG Z, ZHANG J W, FENG J L, et al. Knowledge graph embedding by translating on hyper planes[C]//Proceedings of the 28th AAAI Conf on Artificial Intelligence. 2014: 1112-1119.

[89] LIN Y K, LIU Z Y, SUN M S, et al. Learning entity and relation embeddings for knowledge graph completion[C]//Proceedings of the 29th AAAI Conf on Artificial Intelligence. 2015: 2181-2187.

[90] JI G, LIU K, HE S, et al. Knowledge graph completion with adaptive sparse transfer matrix[C]//Proceedings of the 30th AAAI Conference on Artificial Intelligence. 2016: 985-991.

[91] SUN Z Q, DENG Z H, NIE J Y, et al. RotatE: knowledge graph embedding by relational rotation in complex space[C]//Proceedings of the 7th Int Conf on Learning Representations. 2019.

[92] ZHANG S, TAY Y, YAO L, et al. Quaternion knowledge graph embeddings[C]//Proceedings of the 33rd Conference on Neural Information Processing Systems. 2019: 1-14.

[93] SONG T W, LUO J, HUANG L. Rot-Pro: modeling transitivity by projection in knowledge graph embedding[J]. Advances in Neural Information Processing Systems, 2021, 34.

[94] CAO Z S, XU Q Q, YANG Z Y et al. Dual quaternion knowledge graph embeddings[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2021: 6894-6902.

[95] LI M, JIA Y, WANG Y, et al. Hierarchy-based link prediction in knowledge graphs[C]//Proceedings of the 25th International Conference Companion on World Wide Web. 2016: 77-78.

[96] ZHANG Z, CAI J, ZHANG Y, et al. Learning hierarchy-aware knowledge graph embeddings for link prediction[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2020: 3065-3072.

[97] WANG S, FU K, SUN X, et al. Hierarchical-aware relation rotational knowledge graph embedding for link prediction[J]. Neurocomputing, 2021, 458: 259-270.

[98] HU Z, HUANG P, DENG Y, et al. Entity hierarchy embedding[C]//Proceedings of the 7th International Joint Conference on Natural Language Processing of the Asian Federation of Natural Language Processing. 2015: 1292-1300.

[99] BALAZEVIC I, ALLEN C, HOSPEDALES T. Multi-relational poincaré graph embeddings[J]. Advances in Neural Information Processing Systems, 2019, 32: 4463-4473.

[100] NICKEL M, TRESP V, KRIEGEL H-P. A three-way model for collective learning on multi-relational data[C]//Proceedings of the Int Conf on Machine Learning. 2011: 809-816.

[101] YANG B, YI W T, HE X, et al. Embedding entities and relations for learning and inference in knowledge bases[C]//Proceedings of the 2015 Int Conf on Learning Representations. 2015.

[102] TROUILLON T, WELBL J, RIEDEL S, et al. Complex embeddings for simple link prediction[C]//Proceedings of the Int Conf on Machine Learning. 2016: 2071-2080.

[103] LIU H, WU Y, YANG Y. Analogical inference for multi-relational embeddings[C]//Proceedings of the International Conference on Machine Learning. 2017: 2168-2178.

[104] BALAŽEVIĆ I, ALLEN C, HOSPEDALES T M. Tucker: tensor factorization for knowledge graph completion[J]. arXiv preprint arXiv:1901.09590, 2019.

[105] SOCHER R, CHEN D, MANNING C D, et al. Reasoning with neural tensor networks for knowledge base completion[C]//Proceedings of the Advances in Neural Information Processing Systems. 2013: 926-934.

[106] BORDES A, GLOROT X, WESTON J, et al. A semantic matching energy function for learning with multi-relational data[J].Machine Learning,2014, 94 (2): 233-259.

[107] LIU Q, JIANG H, Evdokimov A, et al. Probabilistic reasoning via deep learning: neural association models[J]. arXiv preprint arXiv:1603.07704,2016.

[108] DETTMERS T, MINERVINI P, STENETORP P, et al. Convolutional 2D knowledge graph embeddings[C]//Proceedings of the 32nd AAAI Conference on Artificial Intelligence. 2018: 1811-1818.

[109] VU T, NGUYEN T D, NGUYEN D Q, et al. A capsule network-based embedding model for knowledge graph completion and search personalization [C]//Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. 2019: 2180-2189.

[110] VASHISHTH S, SANYAL S, NITIN V, et al. InteractE: improving convolution-based knowledge graph embeddings by increasing feature interactions[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2020: 3009-3016.

[111] YAO L, MAO C, LUO Y. KG-BERT: BERT for knowledge graph completion[J]. arXiv preprint arXiv:1909.03193, 2019.

[112] ZHAO Y, ZHOU H, XIE RB, et al. Incorporating global information in local attention for knowledge representation learning[C]//Proceedings of the Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021. 2021: 1341-1351.

[113] 姚思雨, 赵天哲, 王瑞杰, 等. 规则引导的知识图谱联合嵌入方法[J]. 计算机研究与发展, 2020, 57(12): 2514-2522.

YAO S Y, ZHAO T Z, WANG R J, et al. Rule-guided joint embedding learning of knowledge graphs[J]. Journal of ComputerResearch and Development, 2020, 57(12): 2514-2522

[114] GUO S, WANG Q, WANG L H, et al. Jointly embedding knowledge graphs and logical rules[C]//Proceedings of the 2016 Conf on Empirical Methods in Natural Language Processing. 2016:192-202.

[115] GUO S, WANG Q, WANG L H, et al. Knowledge graph embedding with iterative guidance from soft rules[C]//Proceedings of the 32th AAAI Conf on Artiﬁcial Intelligence. 2018:4816-4823.

[116] WANG P W, DOU D J, WU F Z, et al. Logic rules powered knowledge graph embedding[J]. arXiv preprint, arXiv: 1903.03772, 2019.

[117] ZHANG W, PAUDEL B, WANG L, et al. Iteratively learning embeddings and rules for knowledge graph reasoning[C]//Proceed- ings of the World Wide Web Conf. 2019:2366-2377.

[118] CHENG K W, YANG Z Q, ZHANG M, et al. UniKER: a unified framework for combining embedding and definite horn rule reasoning for knowledge graph inference[C]//Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. 2021: 9753-9771.

[119] NEELAKANTAN A, ROTH B, MCCALLUM A. Compositional vector space models for knowledge base completion[J]. Computer Science, 2015:1-16.

[120] SHEN Y, HUANG P S, CHANG M W, et al. Traversing knowledge graph in vector space without symbolic space guidance[J]. arXiv preprint, arXiv: 1611.04642, 2016.

[121] DAS R, NEELAKANTAN A, BELANGER D, et al. Chains of reasoning over entities, relations, and text using recurrent neural networks[C]//Proceedings of the 15th Conf of the European Chapter of the Association for Computational Linguistics. 2017: 132-141.

[122] WANG Z K, LI L J, ZENG D D. Attention-based multi-hop reasoning for knowledge graph[C]//Proceedings of the 2018 IEEE Int Conf on Intelligence and Security Informatics. 2018:211-213.

[123] NIU G, ZHANG Y, LI B, et al. Rule-guided compositional representation learning on knowledge graphs[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2020: 2950-2958.

[124] QU M, TANG J, Probabilistic logic neural networks for reasoning[C]//Proceedings of the Advances in Neural Information Processing Systems. 2019:7712-7722.

[125] ZHANG Y Y, CHEN X S, YANG Y, et al. Efficient probabilistic logic reasoning with graph neural networks[J]. arXiv preprint, arXiv: 2001.11850, 2020.

[126] VARDHAN L V H, JIA G, KOK S. Probabilistic logic graph attention networks for reasoning[C]//Proceedings of the World Wide Web Conf 2020. 2020: 669-673.

[127] COHEN W W. Tensorlog: a differentiable deductive database[J]. arXiv preprint, arXiv: 1605.06523, 2020.

[128] EVANS R, GREFENSTETTE E. Learning explanatory rules from noisy data[J]. Journal of Artificial Intelligence Research, 2018, 61(8): 1-64

[129] YANG F, YANG Z, COHEN W W, Differentiable learning of logical rules for knowledge base reasoning[C]//Proceedings of the Advances in Neural Information Processing Systems. 2017:2319-2328.

[130] WANG P, STEPANOVA D, DOMOKOS C, et al. Differentiable learning of numerical rules in knowledge graphs[C]//Proceedings of the 8th Int Conf on Learning Representations. 2020.

[131] YAN Y, SONG L. Learn to explain efﬁciently via neural logic inductive learning[C]//Proceedings of the 8th Int Conf on Learning Representations. 2020.

[132] WANG S, WEI X K, NOGUEIRA DOS SANTOS C N, et al. Mixed-curvature multi-relational graph neural network for knowledge graph completion[C]//Proceedings of the Web Conference. 2021: 1761-1771.

[133] TERU K K, DENIS E, HAMILTON W L. Inductive relation prediction by subgraph reasoning[J]. arXiv preprint, arXiv:1911.06962, 2019.

[134] DU Z, ZHOU C, DING M, et al. Cognitive knowledge graph reasoning for one-shot relational learning[J]. IEEE Trans on Knowledge and Data Engineering, 2021.

[135] XU X R, FENG W, JIANG Y S, et al. Dynamically pruned message passing networks for large-scale knowledge graph reasoning[C]//Proceedings of the 2020 Int Conf on Learning Representations. 2020.

[136] HO V T, STEPANOVA D, GAD-ELRAB M H, et al. Rule learning from knowledge graphs guided by embedding models[C]//Proceedings of the 17th Int Semantic Web Conf. 2018:72-90.

[137] OMRAN P G, WANG K, WANG Z. Scalable rule learning via learning representation[C]//Proceedings of the 27th Int Joint Conf on Artiﬁcial Intelligence. 2018: 2149-2155.

[138] DONG H H, MAO J Y, LIN T, et al. Neural logic machines[C]//Proceedings of the 7thInt Conf on Learning Reresentations. 2019.

[139] PAN Y, LIU J, ZHANG L, et al. Learning first-order rules with relational path contrast for inductive relation reasoning[J]. arXiv preprint arXiv:2110.08810, 2021.

[140] QU M, CHEN J K, XHONNEUX LP, et al. RNNLogic: learning logic rules for reasoning on knowledge graphs[C]//Proceedings of the 2021 Int Conf on Learning Representations. 2021.

[141] XIA Y, ZHOU G, LUO J Y, et al. PFCA: an intelligent method of multidimensional user profile construction and application[C]//Proceedings of the 2022 Int Conf on big data analytics. 2022:272-279.

[142] LYU X, CAO Y X, HOU L, et al. Is multi-hop reasoning really explainable? Towards benchmarking reasoning interpretability[C]//Proceedings of the 2021 Conference on Empirical Methods in NaturalLanguage Processing. 2021:8899-8911.

Survey on explainable knowledge graph reasoning methods

XIA Yi, LAN Mingjng, CHEN Xiaohui, LUO Junyong, ZHOU Gang, HE Peng

Information Engineering University, Zhengzhou 450001, China

In recent years, deep learning models have achieved remarkable progress in the prediction and classification tasks of artificial intelligence systems. However, most of the current deep learning models are black box, which means it is not conducive to human cognitive reasoning process. Meanwhile, with the continuous breakthroughs of artificial intelligence in the researches and applications, high-performance complex algorithms, models and systems generally lack the transparency and interpretability of decision making. This makes it difficult to apply the technologies in a wide range of fields requiring strict interpretability, such as national defense, medical care and cyber security. Therefore, the interpretability of artificial intelligence should be integrated into these algorithms and systems in the process of knowledge reasoning. By means of carrying out explicit explainable intelligence reasoning based on discrete symbolic representation and combining technologies in different fields, a behavior explanation mechanism can be formed which is an important way for artificial intelligence to realize data perception to intelligence perception. A comprehensive review of explainable knowledge graph reasoning was given. The concepts of explainable artificial intelligence and knowledge reasoning were introduced briefly. The latest research progress of explainable knowledge graph reasoning methods based on the three paradigms of artificial intelligence was introduced. Specifically, the ideas and improvement process of the algorithms in different scenarios of explainable knowledge graph reasoning were explained in detail. Moreover, the future research direction and the prospect of explainable knowledge graph reasoning were discussed.

knowledge reasoning, knowledge graph, explainable artificial intelligence, information security

TP309

10.11959/j.issn.2096−109x.2022063

2022−04−05；

2022−06−13

兰明敬，lanmingjing@126.com

国家自然科学基金（41801313）；河南省科技攻关计划（222102210081, 222300420590）

The National Natural Science Foundation of China (41801313), The Science and Technology Program of Henan Province (222102210081, 222300420590)

夏毅, 兰明敬, 陈晓慧, 等. 可解释的知识图谱推理方法综述[J]. 网络与信息安全学报, 2022, 8(5): 1-25.

Format: XIA Y, LAN M J, CHEN X H, et al. Survey on explainable knowledge graph reasoning methods[J]. Chinese Journal of Network and Information Security, 2022, 8(5): 1-25.

夏毅（1997−），男，辽宁丹东人，信息工程大学硕士生，主要研究方向为知识图谱推理。