MIMO雷达稀疏阵列优化设计方法

唐军奎, 刘 峥,*, 谢 荣, 曾 波

(1.西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 华东电子工程研究所, 安徽 合肥 230088)

0 引 言

多输入多输出(multiple input multiple output,MIMO)雷达指的是各个发射阵元发射不同波形信号,多个接收天线接收的雷达系统。这种信号发射的波形分集使得MIMO雷达在空间分辨率、参数识别能力、低速目标检测等方面比一般相控阵雷达具有更好的性能,成为了近几年雷达界的研究热点[1-7]。MIMO雷达的发射和接收均为多阵元的阵列结构,不同的阵列设计对系统性能具有显著影响。因此,在阵列结构复杂度一定的条件下对MIMO雷达进行稀疏阵列优化,提高其系统的检测与定位等能力至关重要[8-12]。

对目标的角度测量是雷达系统的基本功能之一。传统相控阵雷达中的角度估计方法同样适用于MIMO雷达[13-19],单脉冲测角方法因其实现比较简单、测角精度高、抗干扰能力强等优点,在雷达系统中得到了广泛应用。文献[14]利用全微分方法对MIMO雷达和相控阵雷达测角精度进行了详细的推导和分析。文献[17]对相控阵雷达和MIMO雷达的单脉冲比幅、比相测角方法进行了对比分析。这些单脉冲测角技术的研究都表明MIMO雷达可以利用发射孔径自由度提高其参数估计精度。但是在实际运动平台(机载或弹载)雷达系统中,通常面临布阵空间有限的问题,无法充分利用MIMO雷达天线收发位置获得最大的连续虚拟空间。所以通常考虑优化MIMO雷达的发射和接收阵元位置实现期望的和差波束方向图[20-23]。

低副瓣阵列天线对于提升抗干扰、杂波性能等至关重要[22]。单脉冲估计中,需要对和差波束旁瓣同时抑制以保证测角精度。文献[20]在阵元个数以及可排布阵列最大空间确定的条件下,对MIMO雷达发射阵列和接收阵列联合稀疏优化设计,得到了较窄的主瓣以及较好的旁瓣水平,但仅涉及到和波束。文献[24]提出了一种阵列综合方法,用于设计单脉冲雷达可重构稀疏阵列的和差方向图,与均匀间隔阵列相比,可以获得更好的波束方向图性能和更少的元件数量。当考虑对系统多种性能同时优化时,需要利用多目标进化算法(multi-objective evolutionary algorithm,MOEA),其中某一个目标求得的最佳方案是以其他目标性能下降为代价的[25-29]。文献[28]针对全局最优阵列分布问题,提出了一种多目标粒子群优化搜索算法,在天线单元数量和旁瓣电平方面优于其他算法。文献[29]利用多目标进化算法对相控阵雷达的多种性能进行了优化,使得干扰下的和差波束旁瓣等性能得到同时提升。

本文针对MIMO雷达天线的稀疏阵列优化问题,提出了基于Pareto秩排序的MOEA算法的稀疏阵列设计方法。该方法同时对MIMO雷达单脉冲测角时的和差波束进行优化,相当于在最优和波束和最优差波束之间进行折衷选择,也就是说和波束性能的提高是以牺牲差波束性能为代价的,反之是同样的。由MOEA得到的是最优阵列结构集,可以综合考虑实际需求选择合适的布阵方式。仿真实验验证了本文方法的有效性。

1 MIMO雷达信号模型

本文以运动平台线阵MIMO雷达为信号模型,收发阵列共址。设MIMO雷达的发射和接收阵元分别为M个和N个,发射阵元间距为dT,接收阵元间距为dR,目标位于方位θ。在接收端,通过匹配滤波器分离接收到的目标回波信号,从而在MIMO雷达接收端形成等效发射波束[21-22]。对于单次发射信号,第n个接收阵元接收到的目标反射回波信号经第m个信号匹配滤波后的表达式为

xn,m(θ)=ρEme-j2π(m dT+n dR)sin θ/λ+nn,m

(1)

式中:ρ为发射系数；Em是每个发射信号的能量,这里假设Em=1,即每个阵元发射的信号能量都为1;nn,m为对应的高斯白噪声输出项。

将式(1)中匹配滤波得到的MIMO信号进行列向量化处理,可以得到MN维列向量,表示为

x=[x0,0,x1,0,…,xN-1,M-1]T

(2)

为了使得形成的波束指向特定的方位,使用加权向量ws对匹配滤波器组的输出进行加权。根据空域波束形成理论以及匹配滤波理论,在θ0方向上ws的取值为

ws=wT⊗wR

(3)

式中:⊗表示Kronecker积;wT=[1,e-j2πdTsin θ0/λ,…,e-j2π(M-1)dTsin θ0/λ]T为发射波束形成的权向量;wR=[1,e-j2πdRsin θ0/λ,…,e-j2π(N-1)dRsin θ0/λ]T为接收波束形成的加权向量。

2 MIMO雷达稀疏阵列优化

2.1 MIMO雷达等效收发阵列

与相控阵雷达不同,MIMO雷达在接收端等效形成发射波束以得到联合方向图,再进行和差波束测角[20-22]。首先对式(2)进行分析,假设发射阵元多于接收阵元,各阵元之间间距相同,即M>N,d=dT=dR=λ/2;将各个接收阵元匹配滤波输出的MN个值排成矩阵形式,可以表示为

(4)

通过观察式(4)矩阵形式以及式(1)可以看出,式(4)中与副对角线平行的元素,除噪声不同外,其信号部分完全相同,令fs=2πd/λ,式(4)中信号相位项可表示为

(5)

根据式(5)按副对角线进行合并,得到三角形阵列,如图1所示。可以看出MIMO雷达等效阵列可以通过发射阵列与接收阵列卷积得到。若暂不考虑噪声,则等效阵列相当于对长度为(M+N-1)的均匀线阵进行三角形加权得到,权向量为

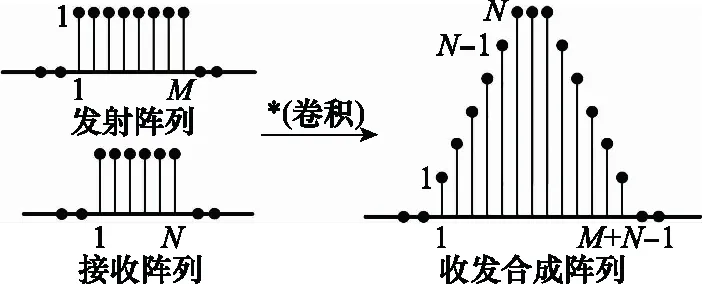
图1 MIMO雷达等效合成阵列

此时,MIMO雷达等效收发波束的权矢量wnew可以表示为

wnew=diag(ws)·Q

(6)

2.2 MIMO雷达稀疏阵列多目标优化函数

对MIMO雷达阵列稀疏优化设计是通过优化其接收和发射阵元的位置实现的。目前MIMO雷达阵列主要的布阵方式有两种:一种是紧凑布阵方式,发射阵列和接收阵列中相邻阵元间距为半波长;另一种是稀疏布阵方式,发射阵列和接收阵列均为相邻阵元间隔d=λ/2的稀疏阵列。其中,规则稀疏布阵和发射阵元间距为接收阵列的孔径,接收阵列按照半波长布置,可以获得最大的虚拟连续孔径。但在机载或弹载平台应用中即使在阵元数不多的情况下也难以实现规则稀疏布阵,此时MIMO雷达阵列通常采用不规则稀疏布阵方式[30-31]。

假设MIMO雷达共有M0个发射位置和N0个接收位置,分别布置M个发射阵元和N个接收阵元。PT是发射阵元位置序号,PR是接收阵元位置序号。PT、PR可以分别表示为PT=[PT,0,PT,1,…,PT,M-1],PR=[PR,0,PR,1,…,PR,N-1],其中PT,0=PR,0=0,PT,M-1=M0,PT,N-1=N0。QT是发射阵元位置构成的M0×1维向量,与PT阵元序号对应的元素为1,其余为0,同时QT中的第一个元素也应该设为1。类似地,QR是接收阵元位置构成的N0×1维向量。则有:

Q0=QT*QR

(7)

式中:*表示卷积。

由式(6)可得MIMO雷达稀疏阵列的等效收发和差波束权矢量为

wΣ=diag(ws)·Q0

(8)

wΔ=diag(diag(ws)·U)·Q0

(9)

式中:U=[-1,-1,…,-1,1,1,…,1]T。

由上述式(8)和式(9),令K=M0+N0,对于不规则稀疏阵列结构的MIMO雷达和差波束可以表示为

(10)

(11)

式中:u=sinθ-sinθ0；(·)*表示复数共轭。

根据参考文献[20],MIMO雷达稀疏阵列设计的和差波束的旁瓣峰值目标函数可以表示为

(12)

(13)

式中:RΣ、RΔ分别为和差波束形成加权系数wΣ,m、wΔ,n之和;uend设置为1,uΣstar、uΔstar的取值可以将主瓣区别于旁瓣。

从式(12)和式(13)可以看出,fΣ、fΔ都是由阵元位置PT和PR决定的。因而,待优化的问题以多目标优化形式可以描述如下:

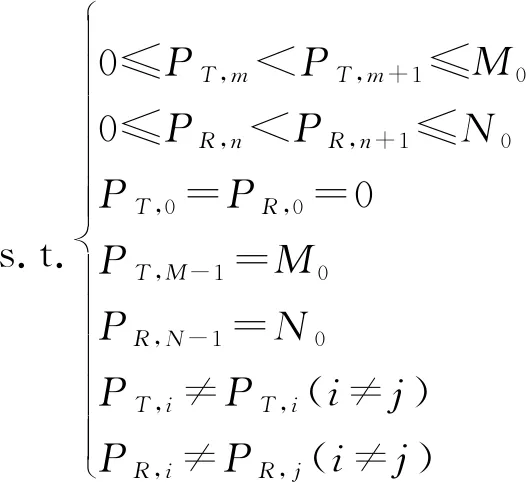
(14)

利用MOEA对式(14)优化所得到的最优解并不是唯一的,而是一个解集合,称为Pareto最优解。所有Pareto最优解对应的目标函数值形成的最优区域称为Pareto前沿,MOEA的优化就是不断逼近Pareto前沿的过程。

2.3 MIMO雷达稀疏阵列优化流程

采用既带有精英保留策略又可以快速非支配排序遗传算法(non-dominated sorting genetic algorithm, NSGA)-Ⅱ作为本文MIMO雷达阵列结构优化的MOEA。NSGA-Ⅱ算法是在NSGA的基础上改进而来的,具有运行速度快、解集收敛性好的优点。算法流程图如图2所示。

图2 NSGA-Ⅱ算法流程图

下面对NSGA-Ⅱ算法阵列优化过程中的主要步骤进行说明:

(1) 产生初始种群G0:在1～(M0-1)之间随机生成(M-2)个从小到大的整数形成向量A,则可得发射阵元位置向量PT=[0,A,M0],同理可得接收阵元位置向量PR。将发射和接收阵元位置矢量结合,种群中个体可以表示为P=[PT,PR]。随机生成若干组向量P得到初始种群G0。

(2) 产生新种群:计算种群个体的序值和拥挤距离。对于两个个体,当序值不同时,选择序值小的个体;若序值相同,选择拥挤距离大的个体。然后将选中的个体通过交叉和变异操作产生子代种群H0,并修正子代H0中的个体使其满足约束条件。

(3) 修剪种群:将Gt和Ht并入到Rt中(初始时t=0),对Rt进行快速非支配解排序,构造其所有不同等级的非支配解集F1,F2,…。按照需要计算Fi中所有个体的拥挤距离,并根据拥挤比较运算符构造Gt+1,直至Gt+1规模等于G0。

3 仿真结果

仿真参数设置如下:设有发射阵元M=16,按d的整数倍间距放置在0～32λ范围内的栅格上;接收阵元N=8,按d的整数倍间距放置在0～16λ范围内的栅格上,其中d=λ/2。设θ0=0,和波束uΣstar设置为0.03,差波束uΔstar设置为0.07。在进化参数中,种群大小为200,迭代代数为100,交叉概率为0.9,变异概率为0.1。原始阵列结构随机选取。

3.1 和波束最优旁瓣电平

图3(a)给出了本文方法稀疏阵列结构优化后和波束的收发联合方向图,为了方便比较,同时给出文献[20]优化后和原始阵列结构对应的方向图。可以看出,本文方法与文献[20]方法优化后的旁瓣峰值水平相当,都可以将旁瓣峰值控制在-20 dB以下,且保持较窄的主瓣宽度,原始阵列结构旁瓣峰值为-11.7 dB,即优化后改善了约8.3 dB。和波束优化对应的发阵阵元位置为[0，4，6，8，14，19，22，23，27，35，40，42，43，44，51，64]×d;接收阵元位置为[0,14,15,20,23,25,26,32]×d。与文献[20]的最优布阵结果相比,发射阵列与接收阵列布置方式存在差异,这是因为:一方面满足约束条件的布阵方式较多,可能会出现不同布阵方式对应相同结果的情况;另一方面使用的优化算法为准最优算法,每次仿真结果存在一些偏差。此外,图3(c)本文方法优化后的阵列在波束指向-40°、0°、10°、30°的方向图,可以看出经优化后的阵列在其他方向扫描时仍能保持良好的旁瓣性能。

图3 和波束优化结果

3.2 差波束最优旁瓣电平

图4(a)给出了本文方法稀疏阵列结构优化后差波束的收发联合方向图,同时给出了由文献[20]和波束最优布阵结果生成的差波束和原始阵列生成的差波束作为对比。可以看出,本文方法对差波束优化后,方向图旁瓣峰值电平得到了改善,优化后和原始阵列的旁瓣电平峰值分别为-16.7 dB和-9.6 dB,即旁瓣峰值改善了7.1 dB,相比于文献[20]给出的布阵方式对应的旁瓣电平峰值-15.4 dB改善了1.3 dB。差波束优化对应的发阵阵元位置为[0,4,7,8,12,16,20,24,28,38,39,43,47,48,51,64]×d;接收阵元位置为[0,14,16,17,19,25,26,32]×d。图4(b)给出了优化后的阵列在其他方向扫描时的方向图,实际中单脉冲测角时只考虑差波束在波束中心指向0°附近时的性能,这里仅是为了说明经优化后的阵列在其他方向扫描时仍能保持良好的旁瓣性能。

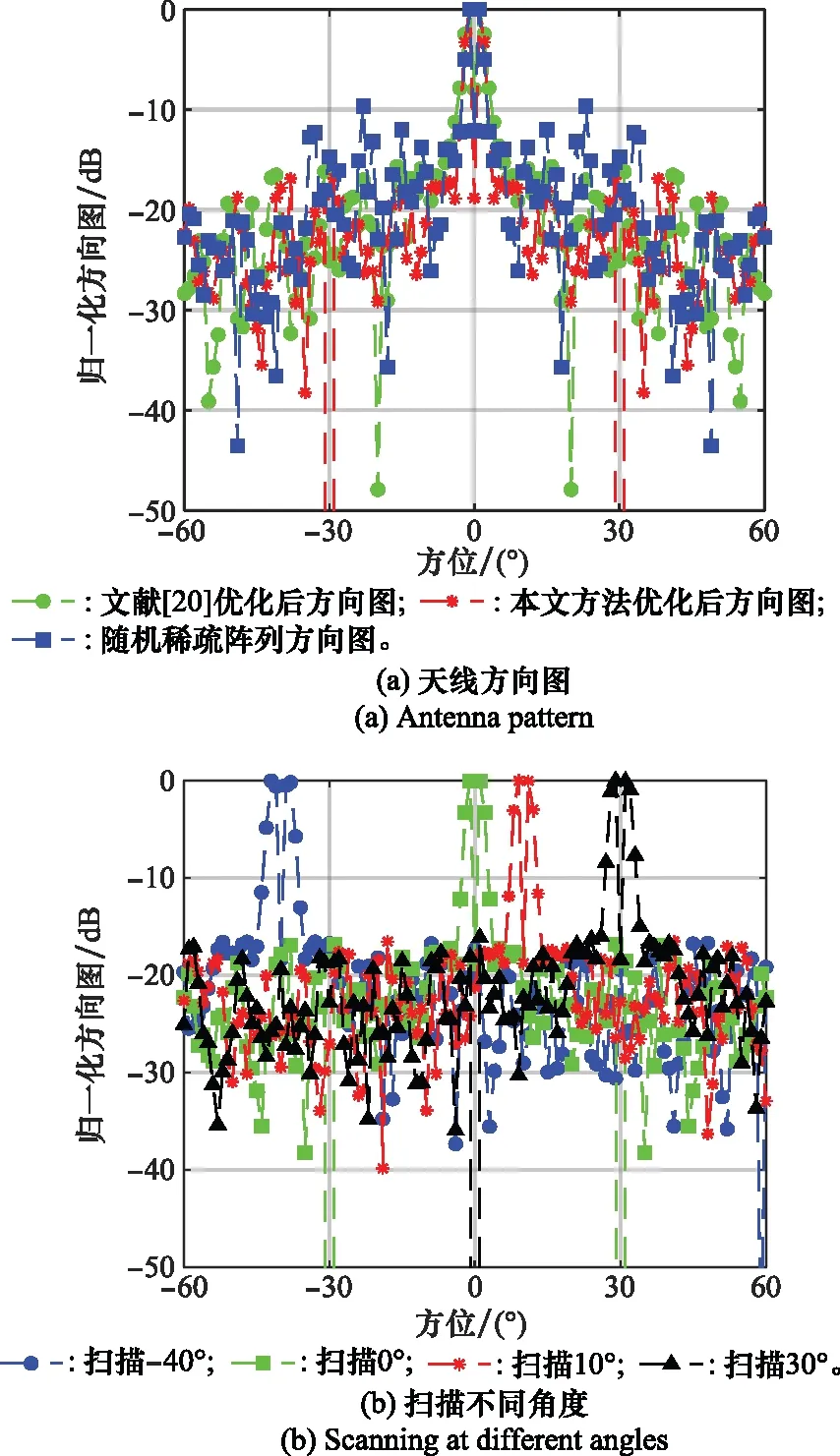
图4 差波束优化结果

3.3 Pareto最优解集

为了验证目标优化性能,图5给出了优化后的和波束、差波束旁瓣峰值电平对应的Pareto最优解。可见最优解分布并不十分均匀,这是由于约束条件的限制,使得部分非法解被剔除的结果。但是从图5中仍可以看到，其具有收敛趋势。同时可以看出,基于Pareto最优解的稀疏布阵设计提供了多种最优布阵方案,可以根据实际需求灵活选择,比如在检测阶段选择和波束最优的稀疏阵列结构即可,可以得到较窄的主瓣以及较好的旁瓣水平,提高对低速目标的探测能力等;在对目标单脉冲测角定位阶段需要同时考虑和差波束旁瓣水平,这时可以选择Pareto前沿中间的目标函数值所对应的阵列结构,相当于对最优性能折衷,获得尽可能好的测角性能。

图5 Pareto最优解

4 结 论

本文首先建立了一般MIMO雷达的信号模型,并推导了其等效合成阵列形成过程,然后给出了稀疏阵列结构下MIMO雷达的和差波束,采用MOEA对MIMO雷达的和波束及差波束同时优化,得到了一个Pareto最优阵列结构解集合,和差波束的旁瓣抑制能力得到了提高。在后续的实际应用中可以根据需求,在得到的最优阵列结构解集合中进行选择,以最终确定所需要的阵列结构。