跨国公司股票价格的时间序列分析及预测

刘庆怡

（首都经济贸易大学统计学院 北京 100070）

股票作为金融市场最主要的金融工具之一，价格往往随时间波动，股票的价格走势直接影响着投资者的经济利益及不同行业的经济状况，股民也遍布世界各地。股票价格的波动趋势是一个国家的政治、经济及生活状况的综合反映。地理位置已不再成为股票市场的障碍，在国际金融活动中，通过一天24小时买卖跨国公司股票和债券，形成了全球性证券交易市场。全球证券市场的形成和发展，促进了世界各国经济的互联互通和跨国公司的发展。

经济的发展与股票市场密不可分，股市能够更广泛地调动和聚集社会闲散资金，为国民经济发展服务；还可以扩大生产和建设规模，促进经济发展。股市还有利于股份制企业筹集资金，满足生产和建设的需要。由于对股票的投资没有时间限制，可以用于长期使用，对股份制公司来说，不需要偿还所筹集的资金，有利于企业的健康经营。股市能够为投资者开辟投资渠道，适应投资者多元化的投资选择。这样灵活的方式可以满足交易和激励的需要，有利于更多的投资者加入并获得良好收益。因此，对股市的精准分析可帮助国家在经济上采取相应的宏观调控，还能帮助投资者更好地做出决策使其获益最大。股票价格能否被预测及如何被预测有着十分重要的研究意义。

由于股市受多方面因素，例如政治政策、国家法规、收入状况和投资心理等的影响，导致股市的内部规律非常复杂，增大了做出准确预测的难度。国内外许多研究者也对股票价格预测做了大量的相关工作，并从各个学术领域提出了许多预测方法。从计量经济学和统计学角度来讲，在股票价格的预测应用上，采用时间序列模型是一种较为普遍的预测方法，它通过序列的统计关系来反映线性动态系统的特征和变化，从而揭示数据本身的变化规律。时间序列包含多种模型，如自回归AR模型、移动平均MA模型、自回归移动平均ARIMA模型、差分自回归移动平均ARIMA模型等，从多种模型中选择一个或几个较为合适的模型进行股票价格预测是极大的考验，但最终选择的相对最优模型也具有很重要的现实意义，能够在个人层面、公司层面提供个人利益最大化和公司发展最大化的参考，甚至在国家层面和世界层面的经济政策提供策略帮助。

一、背景

本文所使用的数据集来自kaggle网站，该数据集压缩包共包含15个子文件数据集，为各种跨国公司的股票数据，股票价格是典型的时间序列数据。本文选取分析的是其中的Tata Consultancy Services Limitedstock即Tata咨询服务有限公司数据集。原数据集中共有3940条数据，8个变量，最终用于时间序列建模的变量有两个，即日期Date和收盘价Close。旨在对日收盘价数据日期为2005/1/3至2020/12/31的股票收盘价进行时间序列分析。最后对未来五日的收盘价进行估计，并与数据集中2021/1/1、2021/1/4至2021/1/7五个交易日收盘价的实际值进行比较。另外，本文将246天作为该股票一年的交易日天数。应用过程中，对原始收盘价数据取对数再进行差分，分析其对数收益率，在建立对数收益率模型的基础上再继续分析原始数据，从而选取相较最优模型对未来五日的股票收盘价趋势进行预测。

二、ARIMA模型介绍

ARIMA模型即差分自回归移动平均模型，最先由Box和Jenkins提出，因此又被称为Box-Jenkins模型，预测对象随时间变化的数据是随机序列，可以用数学模型进行预测和描述，通过使用合适的时间序列模型来列举或预测尚未发生的数据，故ARIMA模型对预测时间序列发展趋势比较有效。面对一个新的时间序列数据，其数据内部的信息是未知的。因此，先对数据进行预处理是非常有必要的，后续可能还需要进行差分处理，以确保经处理后的时间序列是平稳并且非白噪声的，这样才可以用于后续建模，以达到预测未来趋势的目的。而差分就是为了实现时间序列的平稳性，通过对时间序列进行自相关检验和偏自相关检验，再建立适当的ARIMA（p,d,q）模型，其中p为自回归的回归项数，q为移动平均的移动平均项数，d为由非平稳时间序列转化为平稳时间序列需要进行d次差分。面对一个不平稳的时间序列数据，在消除了序列的局部不平稳后，之后的处理与其他时间序列类似。差分后得到的平稳时间序列称为齐次非平稳时间序列，进行一次差分称为一阶齐次非平稳时间序列，进行两次差分称为二阶齐次非平稳时间序列，以此类推。

三、平稳性检验

平稳性是时间序列分析中的重要假设，分为严平稳和弱平稳，严平稳性要求联合分布在时间变化图中要保持不变，该条件限制很严格，通常情况下，只要满足弱平稳条件的序列就被称为平稳时间序列。其基本思想是，决定过程特性的统计规律不随时间改变。当序列是平稳序列时，均值为一个常数，这意味着原本包含多个随机变量的均值序列变成了只包含一个变量的常数序列，这极大地减少了随机变量的个数，并增加了待估变量的样本容量。同时还简化了时间序列分析的难度，提高了特征统计量估计的准确性。因此，在建模之前，对序列做平稳性检验是非常有必要的。本文通过图检验法和单位根检验法来判断序列是否平稳，首先绘制序列的时间序列图和自相关图，如图1所示，根据时序图显示，该序列有增加趋势，无周期特征，根据自相关图显示，在很长的延迟时期内，自相关系数一直为正并且并未很快衰减至零，由此可见原序列为非平稳序列，故需要对序列进行差分处理，使原序列通过差分实现序列平稳。首先，绘制对数收盘价进行一阶差分后序列{∇1nPt}的时序图和偏自相关图，如图2所示，时序图呈现平稳状态，偏自相关图前四阶显著偏自相关，故lags=4。其次，对对数收盘价序列进行单位根检验即ADF检验，该检验是为了验证时间序列是否平稳，原假设是时间序列为非平稳。经检验P值=0.9，单位根原假设不能被拒绝，故序列需要进行差分处理。再对一阶差分后的对数序列{ }

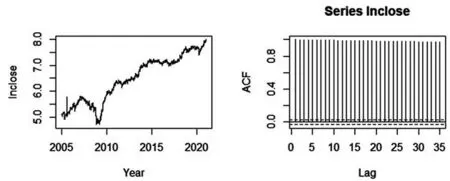
图1 时序图和自相关图

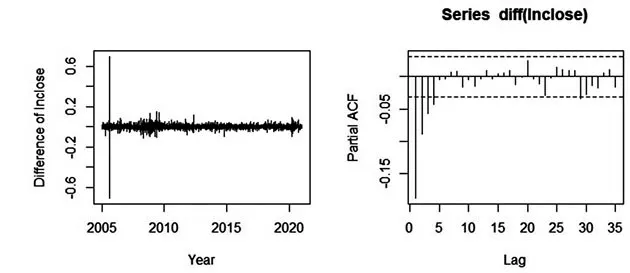
图2 一阶差分后的时序图和偏自相关图

∇1nPt进行单位根检验，先绘制时序图和偏自相关图，接着根据AIC准则最终选择了阶数35，ADF检验p值＜0.01，拒绝对数收盘价一阶差分序列存在单位根的原假设，则原假设经一阶差分后不需要再进行差分，即原序列通过一阶差分实现了序列平稳。值得注意的是，在数据建模前还需要用到白噪声检验，通过鉴别残差来评估所选模型的合理性。在本文数据集的白噪声检验中，p值小于显著性水平0.05，拒绝原假设，显示序列值彼此之间蕴含着相关关系，至此，差分后的对数序列为平稳的非白噪声序列，可用于下一步建模。

四、数据建模

为时间序列数据寻找合适的模型是建模过程中最大的难题，Box和Jenkins书中推崇的多步建模策略应用得最为广泛。该策略由三个主要步骤组成：模型识别（或称模型辨识）、模型拟合和模型诊断，值得注意的是，这三个步骤在建模过程中可循环使用。首先，在模型识别阶段，结合观测数据的特征来选取合适的模型。在这一步骤中，可以通过观察序列的时间序列图用肉眼进行判断，也可以结合生成观测数据的背景知识，如商业、农业、生态学等方面的知识。需要指出的是，目前所选取的模型是暂定的，可在之后的分析过程中联系实际情况进行修正。其次，模型拟合根据模型识别阶段所选取的模型进行参数估计，这一步骤需要做的工作，即找到模型未知参数的最优估计值，最常采用的准则是最小二乘法则和极大似然法则，本文使用的是极大似然法则。最后是模型诊断阶段，在进行了前两个步骤后，需要对拟合的模型进行评价和判断，即模型的质量评估问题。若经过诊断，模型无不足之处，那么数据建模过程也就到此为止。若未通过模型检验，可根据分析过程中的不足寻找其他可能合适的模型，再重复以上三个步骤，直至找到较优策略。

下面，本文将遵循上述多步建模策略进行数据建模，为Tata咨询服务有限公司股票数据集找到合适的时间序列模型。

（一）模型识别

基于自相关图、偏自相关图和扩展的自相关图进行模型识别，现绘制一阶差分后的对数收盘价序列自相关图和偏自相关图，如图3所示，自相关图显示延迟两阶的自相关系数在2倍标准差范围之外，有截尾的性质，偏自相关图显示延迟四阶的偏自相关系数在2倍标准差范围之外，有截尾的性质。综合ACF图和PACF图，拟合模型可初步定阶为MA（2）模型和AR（4）模型。再根据扩展自相关eacf函数结果，还可以考虑ARMA（1,3）模型。另外，基于Akaike信息准则即AIC准则进行模型识别，根据输出差分前序列的结果，故一阶差分前对数序列识别为ARIMA（1,1,1）。

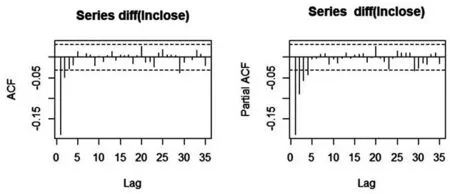
图3 一阶差分后对数序列的自相关图和偏自相关图

综上所述，基于ACF图、PACF图、EACF图和基于AIC准则的模型识别中，对一阶差分后的对数序列{ }∇1nPt最终共识别出四种模型：ARIMA（0,1,2）模型、ARIMA（4,1,0）、ARIMA（1,1,3）模型和ARIMA（1,1,1）模型。

（二）模型拟合

识别出的四种模型：ARIMA（0,1,2）模型、ARIMA（4,1,0）、ARIMA（1,1,3）模型和ARIMA（1,1,1）模型，使用极大似然法分别进行参数估计。由于ARIMA（1,1,3）模型的所有参数均不显著，故最终拟合的模型有三种，分别为：

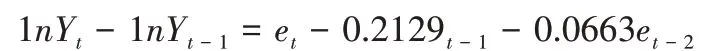
（三）模型诊断

通过参数估计的三种模型进行模型诊断，具体通过分析模型的残差来检验。通常包含残差同方差分析、残差的正态性分析和残差的自相关性分析。检验残差的同方差性一般采用残差图分析法，评价正态性通常使用Q-Q图和Shapiro-Wilk正态检验。为了检验模型中残差项的独立性，通常采用样本acf图法和Ljung-Box检验法，样本acf基本都位于±2/n内，表示这三个模型的残差没有自相关的迹象。Ljung-Box检验的P值若均大于显著性水平，代表没有充分理由拒绝原假设，认为残差项是不相关的。针对上述三个模型，在模型诊断中，残差图有两个异常值点，均未通过残差的正态性检验，均通过了残差的自相关检验。针对异常值点，猜测可能是数据录入有误造成较大的误差，对于未通过残差的正态性检验，可以考虑采用厚尾分布（如学生t分布、广义误差分布等）或者有偏分布（如有偏正态分布、对数正态分布等）作为模型白噪声的分布。

（四）模型比较

经过上述建模分析，最终选出的模型有三种，分别为ARIMA（0,1,2）模型、ARIMA（4,1,0）和ARIMA（1,1,1）模型。将模型诊断和AIC结果汇总，模型比较如表1所示，三种模型的模型诊断结果一致，基于AIC准则，ARIMA（1,1,1）模型的AIC值最小，故在本例中，相较而言，ARIMA（1,1,1）模型为相对最优拟合模型。

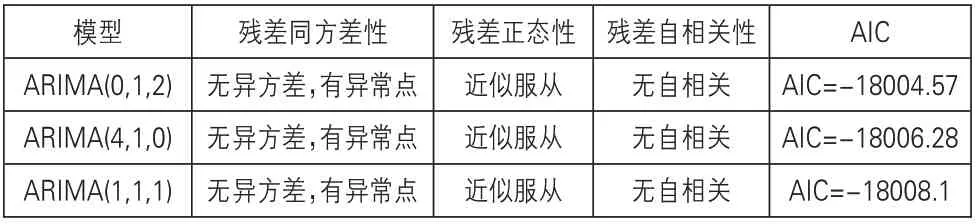
表1 模型比较

（五）模型预测

根据选出的最优模型ARIMA（1,1,1），对其进行未来五日的收盘价预测，预测值和95%置信区间如表2所示，预测图像见图4所示。另外，在原数据文件中查询到未来五日即2021/1/1、2021/1/4—2021/1/7的真实日收盘价值，并计算其平均相对误差为0.05211435，平均相对误差仅为5%左右。

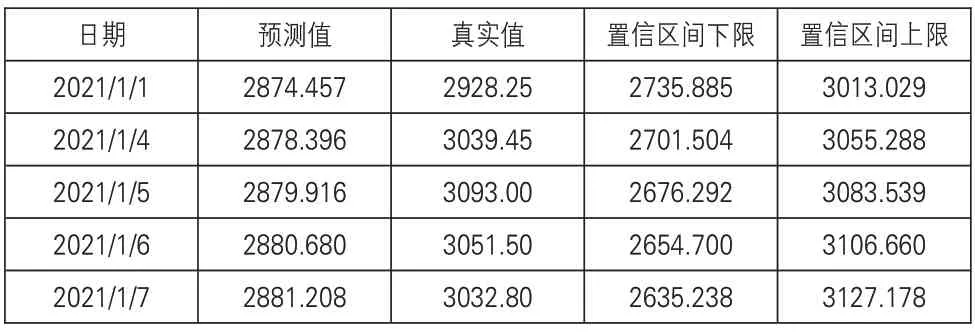
表2 未来五日的预测值和95%置信区间

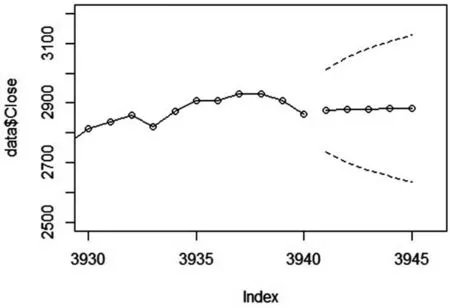
图4 预测图像

五、结语

本文简要介绍了时间序列的相关理论，并对最终使用的模型即ARIMA模型进行了理论知识的详细回顾。对美国跨国公司Tata Consultancy Services Limitedstock股票的日收盘价进行时间序列预测分析，同时实验结果通过R软件进行实现，对其2005—2020年的16年历史股票数据进行了拟合，最终获得了相对较优的ARIMA（1,1,1）模型。模型具体表达式为：

最终将此模型用于未来5个交易日的日收盘价短期预测，将预测值与真实值进行比较得出最终平均相对误差仅为5%左右，从而表明本文所建立的ARIMA模型在进行股票价格短期预测时，效果符合预期。从结果可以得出，ARIMA模型在短期预测上具有一定的可行性，而对于长期预测或者其他突发情形，模型可能会展现出一定的局限性，从而造成较大的估计误差。再加上股票价格本身的数据背景，影响其波动的因素十分复杂，部分因素可能难以量化，如经济政策因素、国际经济环境影响等。考虑到以上不足，还可以采用自回归条件异方差模型、广义自回归条件异方差模型等时间序列模型，这两种模型的综合效果更全面，适用范围更广泛，从而能够使得最终的预测模型更加贴合实际，带来更大的参考价值。