巧借问题链,发展学生的代数推理能力*
——以“立方根”教学为例
2022-11-19朱金霞孙海锋
朱金霞 孙海锋
代数推理是推理的一种类型,初中代数推理是将代数式(或关系)变形为特定的目标结构(或关系),用代数方法证明(或说理)。[1]《义务教育数学课程标准(2022 年版)》指出:“在初中数学中,不仅在图形与几何领域有推理或证明的内容,在数与代数领域也有推理或证明的内容。”[2]由此可见,在初中阶段提高教师代数推理教学的意识,有助于学生理解代数知识,优化思维方式,增强推理能力,提升数学素养。同时能为学生后继内容的学习做好铺垫,有效衔接初高中的数学教学。
因此,笔者尝试在代数概念课的教学中设置环环相扣的问题链,培养学生的代数推理能力。下面,笔者结合苏科版数学教材八年级上册“立方根”的教学片段与大家分享个人观点,不当之处请批评指正。
一、教学片段
1.以“问”促忆,回顾旧知
问题1:同学们,平方根的概念是什么?
生:如果x2=a(a≥0),那么x叫做a的平方根。
追问1:为什么a≥0?
追问2:如何表示a的平方根?
【设计意图】问题1 作为起始之问,帮助学生回忆旧知。追问1帮助学生理解a的含义,凸显平方的非负性。追问2 制造认知冲突,大部分学生会脱口而出±a,忽视了用字母a表示平方根时,a只能是非负数。此环节帮助学生明确在用字母表示数的过程中要注重分类讨论,为研究新知、突破重难点作铺垫。
2.以“问”促思,生成新知
师:有一个小正方体,它的棱长是1。若搭一个棱长是2的正方体,需要4个相同的小正方体;如果棱长是3,需要27个;如果棱长分别是4和5,则分别需要64 和125 个小正方体。(板书23=8,33=27,43=64,53=125……)
问题2:观察这些等式,已知棱长求体积是立方运算;反过来,知道正方体的体积是125,你会求它的棱长是多少吗?
追问1:知道正方体的体积是125 求棱长,是一种什么运算?5叫做125的什么呢?
追问2:如果正方体的体积是2,棱长又是多少?这样的棱长存在吗?
提示:我们不妨设棱长为x,得到x3=2。
追问3:这样的x有几个?如何表示?
追问4:已知立方结果为2求底数x,是一种怎样的运算?x叫做2的什么?
【设计意图】问题2 引导学生运用熟悉的立方运算来计算体积。追问1 提出问题,让学生初步感受在立方运算的等式中涉及底数和幂两个变量,可以已知幂求底数。追问2 使学生产生困惑,在学生原有认知中,没有正整数的立方等于2,打破其原有知识体系。此环节利用4个追问和1 个提示制造思维冲突,引导学生借助数学模型,建立方程解决问题,思考怎样解一元三次方程,引入新的数学符号和数学运算来解决问题。
问题3:同学们能类比平方根的概念,给出立方根的概念吗?
生:如果x3=a,那么x叫做a的立方根。
追问1:为什么不需要a≥0?
追问2:回到问题2中,如何求x3=2中的x呢?
师:a的立方根记作3a,读作三次根号a。类似开平方运算,求一个数的立方根的运算叫做开立方,开立方运算和立方运算是互逆关系。
【设计意图】有了问题1和问题2的铺垫,类比平方根的概念,学生较容易得出立方根的概念。追问1 与复习平方根的概念呼应,形成对比。追问2 用新知解决遗留问题,有助于学生从形式和内涵上分析复杂的代数概念,进一步理解新知。
3.以“问”促探,发展推理
问题4:下列各数有立方根吗?如果有,请写出来;如果没有,请说明理由。

追问1:这些数都有平方根吗?如果有,请写出来;如果没有,请说明理由。
追问2:平方根和立方根有什么联系和区别?
【设计意图】问题4 通过举例引导学生探究立方根的性质,引导学生从定义、个数、表示法、被开方数的取值范围等角度分析平方根和立方根的异同,明确符号的含义,搭建推理运算的阶梯。

【设计意图】问题5 引导学生从互逆运算的角度进行简便计算,明确运算的关系结构,由简单的计算到抽象的推理,为后续验证猜想提供推理依据。平方根和立方根是偶次方根和奇次方根最简单的形式,由此推广到n次方根,对n和被开方数a都要分类讨论,思维和推理的难度都会增大。
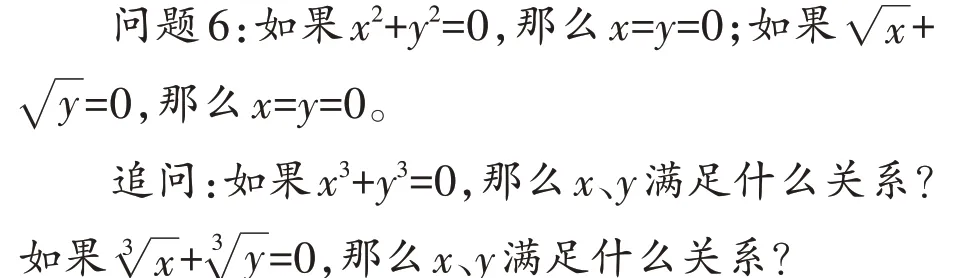
【设计意图】问题6 中先给出两个学生熟悉的真命题,基于平方和算术平方根的特殊性,明确x、y只能等于0。追问则是立方和开立方运算,其中x和y可以是正数、0和负数。这是纯代数推理题,通过演绎推理可以探究x和y的一般关系,引导学生将合情推理和演绎推理有机结合,进一步提升其代数推理能力。
二、几点思考
1.精心设问,体现代数推理教学的内在价值
在概念课的不同教学环节中,教师应立足学生的最近发展区,设置有层次、有梯度的问题,帮助学生深入理解概念,理解数学符号和数学推理运算,建构知识框架。在立方根的教学中,笔者设计以“问”促忆、以“问”促思、以“问”促探三个环节,主问题由浅入深,使立方根的概念、表示、性质等形成体系,逐步优化学生思维,让学生的代数推理能力逐级上升。
2.巧妙追问,挖掘代数推理教学的深度
恰到好处的连续追问,能直接触及概念的核心,突破教学重难点,在关键点处给学生留以足够的思考空间和思考深度,冲破思维定势,形成一系列连续有效的数学思维活动,提升学生的逻辑推理能力。例如,在问题2 之后,设置4个连续追问,推动学生主动探索立方根的存在性和唯一性,顺利引入立方根的概念,用追问将思维引向深处,为后续学习提供思考。
3.适时反问,提升代数推理教学的广度
根据教材内容进行适当拓展、提出反问,不仅能够增加新知的广度,更有利于学生连贯而理性地思考问题。例如,在问题5 中探究关于立方和开立方运算结合的一般规律是对立方根的又一性质探究,若将n次方运算和开n次方运算相结合,则是对任意次方的探究,需要兼顾等式中每一个字母的取值范围。此时需要从代数式的运算角度进行思考,对于含多个字母的等式纯代数推理题,对抽象思维推理能力要求比较高,教学注重广度的同时,需要兼顾不同层次的学生的推理能力,帮助学生掌握数学推理的方法,形成理性精神,提升数学素养。
通过设问、追问和反问形成较为完整的问题链可以驱动课堂教学的深入和发展。有效的问题链设计并非几个问题的简单堆积,而是由有各自功能价值的问题依据特定的内在联系有机组合而成的。[3]在教学过程中,教师要引导学生解决环环相扣、螺旋上升的设问,架构完整的相关代数概念的知识框架,精准理解数学符号和数学运算,拓宽思维的广度;借助层层递进、入木三分的追问和反问,理清数量关系的运算和变形,将合情推理和演绎推理相结合,挖掘思维的深度,渗透数学思想方法,培养代数推理能力。
