面向大数据的数据库划分FP-Growth改进算法

张 乐，魏昕怡，徐 苏,林两位

(1.南昌大学数学与计算机学院,江西 南昌 330031;2.南昌大学际銮书院,江西 南昌 330031;3.数字福建气象大数据研究所(闽南师范大学)，福建 漳州 363000)

在传统的数据挖掘领域，对数据集进行频繁项集挖掘，可以采用经典的Apriori算法[1]和FP-growth算法[2]及一些改进算法。其中，Apriori算法需要多次扫描事务数据库，一来产生很大的I/O负载，二来会产生庞大的候选集，从而占用大量内存空间；FP-growth算法虽然只需两次扫描事务数据库，大大降低了I/O负载，且不产生候选集，从而使算法效率更高[3]，但其算法的基础是需要生成FP树，所生成的FP树同样占用了大量内存空间。

在大数据时代，面对大规模海量数据，单机环境下的存储和计算能力将成为数据挖掘的瓶颈[4]，因此，对传统算法进行改进，利用大数据、并行计算技术等进行频繁项集挖掘成为人们研究的重点。

文献[5-12]都是基于FP-growth算法的采用不同并行处理技术进行频繁项集挖掘的改进的算法，算法效率有所提升。但它们都面临着同一个问题，即在大数据环境下，面对海量事务数据库，在单机中无法存储所生成的FP树，从而导致算法失效。文献[13]采用了投影数据库技术，并通过MapReduce编程模型和并行处理技术实现，在一定程度上解决了以上问题。但在实际应用中，常常会遇到实际可用节点机资源有限及单个节点机内存不足的情况，使该算法的应用有一定局限性；在某些极端情况下还有可能出现某个投影数据库的规模同样很大，甚至接近原始事务数据库的规模，从而同样会导致算法失效的问题。为此，本文提出一种划分数据库的方法，允许用户自行设置所划分的子数据库的规模，从而有效解决实际应用环境中因受单机内存资源的限制而算法失效的问题。

1 传统的FP-growth算法

FP-growth算法使用了一种称为频繁模式树(FP树)的数据结构，FP树是一种特殊的前缀树，由频繁项头表和项前缀树构成。算法分两个阶段进行，第一个阶段是将整个事务数据库压缩到一颗频繁模式树上，第二个阶段是通过对频繁模式树进行挖掘，生成所有的频繁项集。

我们通过一个例子来说明FP-growth算法的过程。假设事务数据库如表1所示，该事务数据库共有10个事务，其中包含a，b，c，d，e，f，g，h共8个项，设定最小支持度计数为min-support=2。

表1 事务数据库DTable 1 Transaction database D

其算法的主要步骤如下：

(1)第一次扫描事务数据库D，得到所有频繁1项集，并对频繁1项按支持度计数的降序排序，得到频繁1项头表L(如表2所示)。其中，f，g和h支持度计数为1，小于最小支持度计数，属于非频繁项，因此它们不会出现在频繁1项集头表L中。

表2 频繁1项集头表LTable 2 Frequent 1-item set

(2)FP树构造：首先创建树的根节点，用“null”标记。第二次扫描数据库D，在FP树中为每个事务创建一个分枝，分枝中的每个节点对应该事务的每一个项(删除非频繁项)，且按表L中的顺序链接，同时分枝中的每个项计数加1。最后，建立频繁1项头表与FP树的关联，得到如下图1所示的FP树。

图1 FP树Fig.1 FP Tree

(3)对以上生成的FP树进行挖掘，得到全部频繁项集。挖掘的过程是通过调用以下过程递归实现的：

Procedure FP-growth(tree,α)

IF tree含单个路径P THEN

FOR each路径P中节点的每个组合(记作β)

产生模式β∪α，其支持度等于β中节点的

最小支持度计数；

ELSE

FOR tree的头表中的每个αi

{产生模式β=αi∪α，其支持度等于αi；

构造β的条件模式基，然后构造β的条件FP树treeβ；

IF treeβ≠Φ THEN

调用FP-growth(treeβ,β)；

}

2 FP-growth算法的改进

FP-growth算法在事务数据库规模不是很大，FP树能够在单机内存中存储下的情况下是有效的。但在大数据环境下，面对海量数据库，所构建的FP树根本无法在单机内存中存储，这种方法也就失效了。为此，我们对传统的FP-growth算法进行改进。我们仍然以前面的事务数据库D为例，说明具体的改进方法。本算法的运行环境是一个由一台mater主机和多台slave节点机组成的并行计算环境。在这种运行环境下，改进后的算法的实现过程如下：

(1)第一次扫描事务数据库D，得到所有频繁1项集，并对频繁1项按支持度计数的降序排序，得到频繁1项头表L(如表2所示)。这一步跟传统FP-growth算法相同。

(2)对事务数据库D进行数据清理，将D中的所有非频繁1项删除。然后对D按每个频繁1项(表L中第一个项b除外)进行抽取，为每个频繁1项建立一个所有事务均含该项的投影数据库。a，c，d，e对应的投影数据库分别如表3～表6所示。

(3)由投影数据库去直接生成的FP树仍然有可能规模庞大，在单机内存中无法存放。为此，我们对以上投影数据库进行进一步的划分，按预先设定所含最大事务数的方式，将投影数据库分成一个个投影子数据库。例如，上例中我们设定所有划分后的投影子数据库中包含的事务数最大为4，则a和c的投影数据库各被进一步划分成两个投影子数据库Da:1，Da:2和Dc:1，Dc:2，如表7～表10所示。

表3 a对应的投影数据库DaTable 3 The corresponding projection database Da with a

表4 c对应的投影数据库DcTable 4 The corresponding projection database Dc with c

表5 d对应的投影数据库DdTable 5 The corresponding projection database Dd with d

表6 e对应的投影数据库DeTable 6 The corresponding projection database De with e

表7 a对应的投影子数据库Da:1Table 7 The corresponding projection sub-database Da:1 with a

这些投影子数据库被分发在一个个节点机上。

(4)每个节点机对投影子数据库进行扫描，构造对应项的投影FP子树。在这里我们需要对传统FP-growth构造FP树的算法加以改进。设第k个节点机处理的是频繁1项m对应的投影子数据库Dm:i。在对Dm:i中的每个事务处理时，首先将每个事务中的项按表L的次序排序，并将m以及其后的所有项全部删除，只将剩余的项在拟构造的FP子树中生成分枝。具体算法如下：

① 创建FP子树的根节点，以“null”标记。

② 遍历数据库Dm:i，对Dm:i中的每个事务执行：

a.将事务中的项按L中的次序排序，并将m以及其后的所有项全部删除，形成事务项列表记为[p│P]，其中p为第一个项元素，而P为剩余项元素的列表。

b.调用insert_tree([p│P]，T)。insert_tree([p│P]，T)执行过程如下：如果T有一个子女N使得N.item-name=p.item-name，则N的计数增1，同时头表中其对应项支持度计数增1；否则创建一个新节点N，将其计数设置为1，链接到它的父节点T，同时头表中添加一项，支持度计数设置为1。如果P非空，递归地调用insert_tree([p│P]，T)。

表8 a对应的投影子数据库Da:2Table 8 The corresponding projection sub-database Da:2 with a

表9 c对应的投影数据库Dc:1Table 9 The corresponding projection sub-database Dc:1 with c

表10 c对应的投影数据库Dc:2Table 10 The corresponding projection sub-database Dc:1 with c

由此改进算法生成的FP树称为频繁1项m所对应的投影子数据库的FP子树Tm:i，为a，c，d，e构建的投影FP子树分别如图2～图7所示。

(5)每个节点机对所构建的FP子树进行挖掘，产生局部频繁项集。设某节点机处理生成的m的FP子树为Tm:i，则由条件FP子树挖掘频繁项集的算法如下：

图2 a的投影FP子树Ta:1Fig.2 Projection FP subtree Ta:1 with a

图3 a的投影FP子树Ta:2Fig.3 Projection FP subtree Ta:2 with a

图4 c的投影FP子树Tc:1Fig.4 Projection FP subtree Tc:1 with c

图5 c的投影FP子树Tc:2Fig.5 Projection FP subtree Tc:2 with c

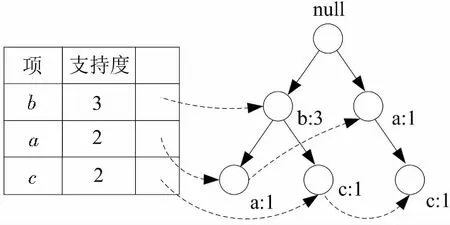
图6 d的投影FP子树Td:1Fig.6 Projection FP subtree Td:1 with d

FOR从树Tm:i根节点null开始的每一条路径R

FOR路径R中的每个节点p

产生模式C=p∪m，其支持度计数等于C中各节点支持度计数的最小值

FOR路径R中的每个节点组合P

局部频繁模式=P∪m，其支持度计数等于C的支持度计数

(6)将同一个频繁1项的投影子数据库生成的局部频繁项集汇聚到同一个节点机进行归并，产生该频繁1项的频繁项集。

(7)最后汇总所有节点机生成的频繁1项对应的频繁项集，从而得到全部的频繁项集。

图7 e的投影FP子树Te:1Fig.7 Projection FP subtree Te:1 with e

3 并行频繁项集挖掘实现

改进后的频繁项集挖掘分为两个阶段：第一阶段生成全部的频繁1项集，并构建频繁1项头表L，我们可以使用MapReduce编程模型并行实现[14,15]；第二阶段由多个节点机并行挖掘频繁项集，最后汇总得到全部的频繁项集。

第一阶段实现过程如下：

(1)在master主机上将事务数据库中的事务分成相同的n个数据块，然后把n个数据块发送到n个slave节点机。

(2)每个slave节点机进行并行Map处理，计算出局部的1项集及其支持度计数；然后通过Combiner函数合并相同项，并把结果发送给master主机。

(3)master主机进行Reduce处理，将所有slave节点发送来的结果进行汇总，计算出全局频繁1项集及其支持度计数，然后按支持度计数值对频繁1项集降序排序，最终得到排序后的结果头表L(如表2所示)。

由于采用MapReduce模式并行实现，这一过程所花费的时间将比传统FP-growth算法更少。

第二阶段实现过程如下：

(1)首先每个节点机对此前master分发来的数据块进行数据清理，将数据块中的所有非频繁1项删除。然后对数据块进行频繁1项抽取，为每个频繁1项生成部分投影数据库，同一频繁1项的所有部分投影数据库被汇聚到同一节点机，生成所有记录都包含该频繁1项的投影数据库。

(2)由slave节点机对每个投影数据库进行进一步的划分，按预先设定所含最大事务记录数的方式，将投影数据库分成一个个投影子数据库。

(3)每个slave节点机为投影子数据库生成对应的FP子树，并对这些FP子树进行挖掘生成局部频繁项集。

(4)同一投影数据库对应的所有子数据库生成的局部频繁项汇聚到同一节点机上，生成该投影数据库对应的频繁项集，然后将结果发送给master主机。

(5)master主机将所有结果汇总后得到的就是全部的频繁项集。

4 算法实验分析

传统的FP-Growth算法在面对海量事务数据库时将会遇到因所生成的FP树规模庞大而无法在单机内存中存储从而导致算法失效这一问题已在文献[12]中进行了验证。本文所提出的算法因为采用了数据库划分的方法，不会存在这一问题。因此，本实验主要针对本文所提出的划分数据库算法(记为DPFP算法)在并行计算环境下的运行效率进行分析。实验方法主要是将DPFP算法在Hadoop集群环境下的运行时间与传统的FP-growth算法在单机环境下的运行时间进行比对。Hadoop集群环境采用主从式架构，包括1个master主机(配置为Intel i7-9700 CPU，16GB内存)和最多10个slave节点机(配置为Intel i5-2450 CPU，4GB内存)。

实验一：DPFP算法分别在由1台master主机加5台slave节点机和1台master主机加10台slave节点机组成的集群环境上运行，FP-growth算法在单台节点机上运行。实验数据集选取Frequent Itemset Mining Data Repository[16]里的T1014D100K.dat，该数据集包含10万条记录。其中设定的最小支持度分别为2%，4%，6%，8%和10%。实验结果分别如图8，9所示。

从运行结果看：

(1)DPFP算法在执行效率上比传统的FP-growth算法更高，且节点机数量越多，DPFP算法所需的时间越少，这也体现了并行处理的优势。

(2)随着最小支持度数值的增加，两种算法的挖掘时间都逐渐减少。这是因为最小支持度数值越大，频繁项越少。对FP-growth算法来说，最小支持度数值越大，生成的FP树越小，对FP树递归挖掘的时间也就越少；对DPFP算法来说，最小支持度数值越大，生成的频繁1项投影数据库越少，分发数据的时间就越少，对投影子数据库进行挖掘的时间也就越少。

(3)DPFP算法相比FP-growth算法的加速比并不会随着最小支持度数值的增加而成线性增长[17]，这是因为最小支持度越大，DPFP算法中所进行的投影数据库生成和分发所占的时间比值越大，而这些操作在FP-growth算法中是没有的。因此，当最小支持度逐渐增大后，FP-growth算法所生成的FP树越来越小，递归挖掘的时间会越来越呈线性递减的趋势。

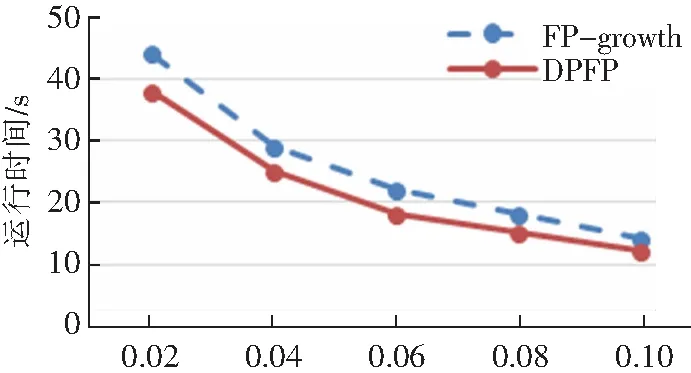
最小支持度图8 实验一5台节点机Fig.8 Experiment 1:5-Node machines

最小支持度图9 实验一10台节点机Fig.9 Experiment 1:10-Node machines

实验二：DPFP算法在由1台master主机加10台slave节点机组成的集群环境上运行，FP-growth算法仍然在单台节点机上运行。实验数据由IBM QUEST Market-Basket Synthetic Data Generator产生，选取包含100万条记录的事务数据库。设定的最小支持度同样分别为2%，4%，6%，8%和10%。实验结果如图10所示。

从运行结果看，随着事务数据库规模的增大，DPFP算法的效率更加明显。这是因为数据库规模越大，FP-growth算法生成的FP树就越大，递归挖掘庞大的FP树将非常耗时。而对DPFP算法来说，投影数据库生成和分发所占的时间比值变得更小，且因为DPFP算法划分的子数据库规模接近，分配到各节点机的负载更均衡，由多个节点机并行处理的效率更加显现出来。

最小支持度图10 实验二10台节点机Fig.10 Experiment 2:10-Node machines

5 总结

本文所提出的算法基于传统的FP-growth算法进行改进，并通过Hadoop架构和MapReduce编程模型实现。在该算法中，首先对所有频繁1项生成投影数据库，再对投影数据库进行划分。由于用户可以灵活设置所划分的子数据库中事务记录的数量，因此可以有效控制由这些子数据库生成的FP子树的规模，从而有效解决因FP树在单机内存中存储不下导致算法失效的问题。同时由于采用MapReduce编程模型实现并行FP子树的生成和挖掘，且分发到各节点机的用于生成FP子树的子数据库规模接近，使得各节点机上的负载更均衡。在大规模集群环境下使用该算法可以很好地解决对大数据的挖掘。