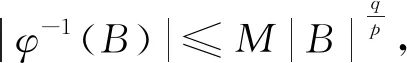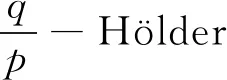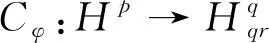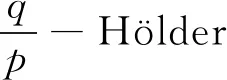拟共形映射下不同指数Hardy空间的复合算子

许姗姗，唐树安

(贵州师范大学 数学科学学院，贵州 贵阳 550025)

0 引言

用Δ={z∈:|z|<1}表示全平面上的单位圆盘，S1={z∈:|z|=1}表示单位圆周，H(Δ)表示单位圆盘Δ上所有解析函数构成的空间。 设φ∈H(Δ)且φ(Δ)⊂Δ， 复合算子定义为

Cφf=f°φ，f∈H(Δ)

解析函数空间中的复合算子得到了广泛的研究，其基本性质和重要结果请参考文献[1-2]。 一个有趣的问题是如果诱导函数φ是一个拟正则映射，也即是一个解析函数复合一个拟共形映射，那么复合算子Cφ有什么性质？ 此时，复合算子Cφ将解析函数空间或者拟正则函数空间映成一个拟正则函数空间。 实际上，我们对这类算子性质了解得很少，它的研究涉及函数空间理论与拟共形映射理论。 王子鹏等[3]研究了由拟共形映射诱导的复合算子在Bergman空间中的有界性，得到很多有趣的结果。 最近，在文献[4]中，作者给出了由拟共形映射诱导的复合算子在相同指数的Hardy空间与Bergman空间中有界的充要条件。 本文将研究这类复合算子在不同指数的Hardy空间与Bergman空间的有界性。 我们首先从一些定义和记号开始。

我们称单位圆Δ内一个解析函数f∈Hp，0

Hp空间上的函数f几乎处处有非切向极限值

T(ζ)={z∈Δ:|z-ζ|

更多关于解析函数的Hardy空间理论，可见参考文献[5-8]。

我们称单位圆Δ内一个解析函数f∈p，0

关于Bergman空间理论的相关内容可以参考[9]。

则称f:Δ→R2是一个K-拟正则映射, 其中

在文献[4]中，Adamowicz和González考虑由拟共形映射φ:Δ→Δ诱导的复合算子。 他们给出了Cφ在Hardy空间与Bergman空间中有界性的充要条件，这些结果既是经典的解析Hardy空间中复合算子的相应结果的推广，又具有独立的研究意义。 为了叙述他们的结果，我们先给出一些定义和记号。

一个复值函数f的导数表示为

如果f是解析的，f′(z)=fz。 我们用dm(z)表示1、2维空间的Lebesgue测度。 记号XY表示X≤MY，XY表示X≥MY，X≈Y表示XYX，其中M为大于零的任意常数。

设0<α≤1, 单位圆周S1上一个函数h称为α-Hölder连续的，如果存在常数M>0， 使得

如果α=1，我们称h是Lipschitz连续的。

Adamowicz和González在文献[4]中给出了在拟共形映射下相同指数的Hardy空间复合算子的有界性。

下面定理是本文的主要结果，我们讨论了由拟共形映射诱导的复合算子在不同指数的Hardy空间的有界性条件。

定理2推广了由解析函数诱导的复合算子在经典解析Hardy空间的情形(见[13-14])。 我们不知道条件“φ-1的导数存在且连续”是否可以去掉，一般来讲，一个拟对称映射可以是不绝对连续的，α-Hölder连续性也不能保证φ-1|S1是可微的。

1 定理2的证明

设z∈Δ， 定义单位圆周S1上的一个与点z相关的区间Iz为

单位圆以z为心的双曲球定义为

Bz=B(z,M(1-|z|))，0

设I是S1上的区间，|I|表示区间I的长度。 集合

称为一个Carleson盒子。

为了证明定理2，我们需要如下引理，它是[4]中引理2的推广。

证设φ(z)=w表示双曲球B的中心。 由K-拟共形映射的偏差引理([11-12,15])，存在常数M， 使得对所有z∈Δ，

diamφ-1(B)≈1-|z|

且

设w0∈Δ，φ-1(w0)=z0，J是S1上的一个区间使得J=Iw0， 由偏差引理可知存在常数M1>0， 使得

又注意到|Iz0|≈1-|z0|，|Iw0|≈1-|w0|， 我们有

引理证毕。

我们也需要下述引理。

引理2[4]设K≥1，φ:Δ→Δ是一个K-拟共形映射，T(ζ)是以ζ∈S1为顶点的锥，那么

φ(T(ζ))⊂Tφ(ζ)。

下面开始定理2的证明。

(1)

根据法图引理和(1.1)，有

(2)

定义S1上的测度为μ(A)=m(φ-1(A))， 这里A⊂S1。 通过变量替换，(1)可以表示为

(3)

若z∈Ia， 则

(4)

由(3)和(4)，我们推出

根据μ的定义，可知

由引理2以及(φ-1)′存在且连续，我们推出存在常数M1>0，使得