市场监管对伴有内部信息的欧式期权超复制定价的影响
2022-11-18李伟方周永辉
李伟方,周永辉
(1.贵州师范大学 数学科学学院,贵州 贵阳 550025;2.贵州师范大学 大数据与计算机科学学院,贵州 贵阳 550025)
0 引言
1973年,Black等[1]建立了无套利基础上的期权定价理论。通过连续调整由股票和无风险债券组成的投资组合,投资者可精确地复制该股票上任何期权的回报,且期权价格就等于复制期权回报的投资组合的值。而当存在比例交易成本时,由于扩散过程具有无限变差,复制期权回报的投资组合的值都会变得无限高,Black-Scholes的期权定价理论不再适用。1985年,Leland[2]给出了一种依赖交易成本大小与修正频率的期权复制策略,得到了比例交易成本时Black-Scholes期权定价的逼近。1989年,Karatzas[3]在期权定价中使用了超复制策略来复制投资组合。1990年,Merton[4]开始在离散时间框架中建立期权定价问题,并得到存在比例交易成本时的期权价格。1995年,Kusuoka[5]证明了比例交易成本的离散时间金融模型中,超复制价格存在尺度极限,并给出了其表达式。其中,超复制价格定义为允许通过某种投资组合策略对冲期权回报的最小初始资本。
2004年,Cetin等[6]通过引入随机供给曲线构建了连续时间的非流动性市场模型。2013年,Dolinsky等[7]在离散时间通过引入二次交易成本构建非流动性市场模型,将交易成本扩展到了由比例交易成本与二次交易成本组成的非线性交易成本,证明了当该市场存在确定波动率时超复制存在尺度极限,并给出了其表达式。进一步,2014年,Bank等[8]也给出了市场存在不确定波动率并超复制尺度极限的表达式。有关在没有市场摩擦且具有不确定波动率的连续时间金融模型中的超复制定价问题的研究见[9-11]。2015年,Bank等[12]研究了存在多个风险资产下的具有比例交易成本的超复制尺度极限问题。2019年,Bank等[13]考虑了交易成本依赖时段的超复制存在尺度极限问题。2021年,Dolinsky等[14]首次考虑了内部信息对超复制的影响,证明了在二次交易成本且波动率不确定的条件下超复制价格存在尺度极限,并给出了其表达式。其它关于内部信息对效用最大化影响的研究见[15-16]。
实际上,内部交易者利用私有信息获利而损害噪声交易者的利益,受到广泛关注。美国国会分别在1984年和1988年颁布了《内部交易制裁法》和《内部交易与证券欺诈执行法》,增加了对被定罪内部人的处罚。1996年,Shin[17]在内部交易模型中引入监管准则,并得出容忍一定数量的内部交易可能是最优监管策略。2019年,Liu等[18]发现,当市场监管存在时,理性内部交易者与启发性内部交易者更倾向于不那么激进的交易,而获得更多的期望利润。2020年,张铁红等[19]研究了理性内部交易者、启发性内部交易者和做市商均收到部分风险资产公共信息时的内部交易监管市场,并证明了该市场的最优交易策略、有效定价规则和最优监管力度组成的线性Bayesian-Nash均衡的存在唯一性。
本文将研究一类具有内部信息、交易成本和市场监管的欧式期权超复制定价问题,讨论超复制价格的尺度极限,并考察市场监管对该极限的影响。
1 模型描述

下面,我们将考虑该市场伴有内部信息、交易成本和市场监管的欧式期权的超复制定价问题。由于实际市场是离散时间交易,因此我们将[0,1]区间n等分以考虑离散情况,进而研究当交易阶段数n趋于无穷时超复制格的尺度极限。本文的模型在文献[14]中模型的基础上,引入了市场监管[17],具体描述如下:
(i)样本空间与股票离散化价格

其中标准过程Xk(ω)=xk,∀ω=(x1,x2,…),且s∈R是常数。
(ii)内部信息与内部交易策略
固定n′∈Ν,假设投资者可看到未来n′阶段的股票信息,即投资者的信息滤子为
Gk=σ{X1,…,Xk+n′},k∈Z+=Ν∪{0}
因此,n阶段模型的内部交易策略是一映射γ:{0,1,…,n-1}×Ω→R,其中∀k=0,1,…,n-1,γk为Gk可测函数,表示投资者在k阶段选择持有股票份额的数量。
(iii)监管者发现内部交易情况与监管策略

(iv)内部交易策略的市值
假设内部交易的成本为二次函数φ→Λφ2,其中Λ>0是一常数且φ是股票的交易量。


其中,k=0,1,…n-1,且γ-1≡0。

(v)超复制价格
本文的主要问题就是研究超复制价格的尺度极限
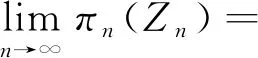
进而,讨论市场监管对该尺度极限的影响。
为了研究尺度极限,还需要在集合D[0,1]中引入适当拓扑结构。通常地,引入skorohod度量:
其中χ:[0,1]→[0,1]严格增,且χ(0)=0,χ(1)=1。
进一步假定未定权益函数H:D[0,1]→R+关于skorohod度量拓扑Lipschitz连续。
显然,如无市场监管,该模型与[14]中的模型相同。
2 主要结果及证明
引理1 对任意n,有下列不等式成立
其中P是Ω上所有概率测度构成的集合。
证明令y∈R且γ是一交易策略使得
则∀p∈P,有
(Λ+β)(γi-γi-1)2))]
(Λ+β)(γi-γi-1)2))]
≤y+(1-q)
(1)
类似文献[14]的性质2.2的证明,同样可以得到超复制价格πn(Zn)的尺度极限的下界,即定理1,略去其证明。
定理1 令H:D[0,1]→R+关于skorohod度量Lipschitz连续,且∃C,μ使得


为了得到超复制价格πn(Zn)的尺度极限的上界,给出下面的定义1。
定义1 1)∀k∈Ν,定义样本空间
2)对任意未定权益Borel可测函数Z:Ωk→R+,定义相应超复制价格
显然,∀k∈Ν,Ωk⊂Ωk+1⊂Ω。我们有下面的结果。
引理2 ∀n∈Ν,
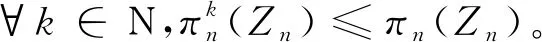
=inf{y∈R:∃γk,s.t.y≥Zn(ω)-(1-
≤inf{y∈R:∃γk,s.t.y≥Zn(ω)-(1-
≤inf{y∈R:∃γk,s.t.y≥Zn(ω)-(1-
=πn(Zn)

另一方面,不失一般性,假设γk关于k在Ν上一致有界。事实上,∀k∈Ν,令y∈R与交易策略γk使得
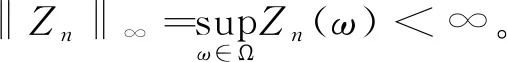
一致有界,所以,可选择y≤‖Zn‖∞。再结合Zn≥0,得到
≥0,∀ω∈Ωk
进而,有


则∀y∈R,


因此


最后,由H的连续性

则

由引理2,∀n∈Ν,存在k=k(n)使得
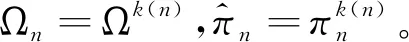
(2)
定义2 ∀ε∈(0,1),n∈Ν,如下递归定义Ωn上的停时列:

令
其中Ι表示示性函数。
类似[14]中引理4.2的证明,可得下面的引理,略去其证明:
引理3 ∀ε,λ∈(0,1),当n足够大时,有
其中,
K=K(ε,λ)=[c(λ)/(ελ)2]+1,c(λ)>2
从而,有下面的结论:
引理4 存在λ0∈(0,1),使得∀ε>0,0≤λ<λ0,n=1,2,…

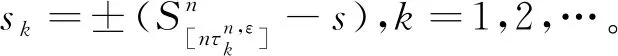
同理,有

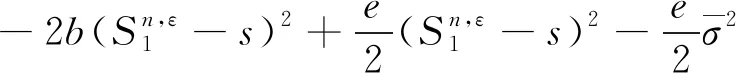
其中,不等式右边的最后两项是对交易成本的估计。因此,根据柯西不等式

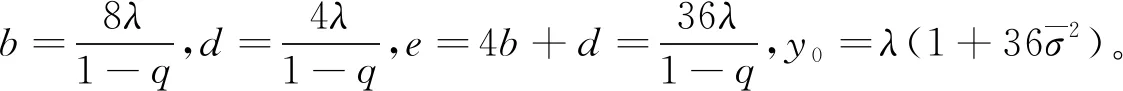
当0≤λ<λ0,有
在引出引理5之前,先给出下面的定义。

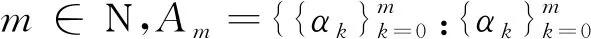
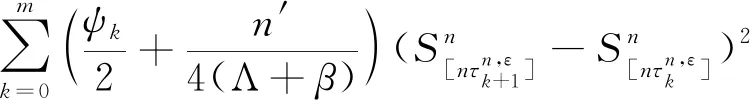

类似地,对k=0,1,…,m,令ck=ak+1-[n1/3]。∀k=0,1,…,m+1,在时间区间[ak,ak+1-1]上定义交易策略γ。
若ak>n-2n1/3,则不在[ak,ak+1-1]上交易。否则,对足够大的n,有bk 在[ak,bk)上以常速进行交易,且股票份额的数量从0变到φk。 在[bk,ck)上,∀i∈[bk,ck),交易 即 (3) 最后,在[ck,ak+1-1]上以常速清算投资组合。 因此,同理(1)式的做法,有 进一步,由(3)式与Sn在[0,am]上一致有界的事实,有 -Ο(n-2/3) 类似地,有 -Ο(logn2/n1/6)-Ο(n-2/3) -Ο(logn2/n1/6)-Ο(n-2/3) 从而, 在引出引理6之前,先给出下列定义。 且 引理6 其中, 类似[14]中引理4.7的证明,即可得: 引理7 根据(2)式与引理3、4、6、7,我们得到下面的定理。 定理2 令H:D[0,1]→R+关于skorohod度量Lipschitz连续,则超复制价格πn(Zn)的尺度极限满足下列不等式 证明由(2)式,只需证 从而,有 +Ο(ε+λ) )(引理6) 因此,结合定理1与定理2,我们得到下面的定理。 定理3 令H:D[0,1]→R+关于skorohod度量Lipschitz连续,则超复制价格πn(Zn)的尺度极限为 在上面的主要结果定理3的基础上,进一步考虑当投资者看到未来交易的阶段数趋于无穷时,超复制价格的尺度极限的变化,我们得到下面的推论。 推论1 证明对等式左边,取v≡0可得 另一方面,根据Doob不等式与H的Lipschitz连续性,存在一常数L使得 从而, 在这部分,我们的目的是站在市场监管者的角度,研究内部交易发现概率的变化对欧式期权超复制价格的尺度极限所带来的影响。 首先,对不存在市场监管的情况,有q=0,亦有β=0。此时, 与文献[14]中结果保持一致。 其次,当存在市场监管时,根据惩罚交易量平方的倍数α与二次成本函数的系数Λ大小的比较,可分为三种情况。 ①对于α=Λ的情况,有 ②对于α>Λ的情况,有 ③对于α<Λ的情况,令 则, 将其关于q求导并令为零,有 A*q2+B*q+C*=0 其中, A*=3E>0,B*=-(4E+2D),C*=2D+E。 最后,当市场监管者发现内部交易的概率q=1时,超复制价格的尺度极限的表达式为 (4)
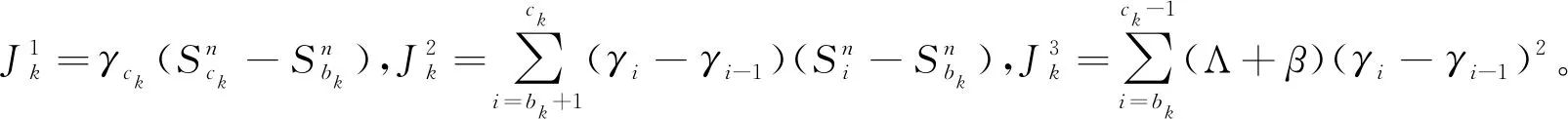
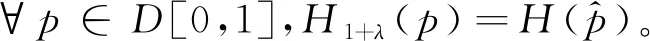
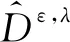
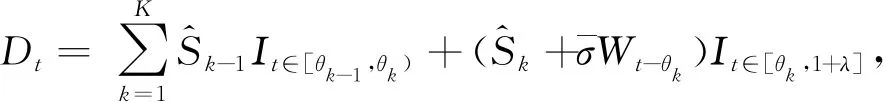
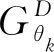



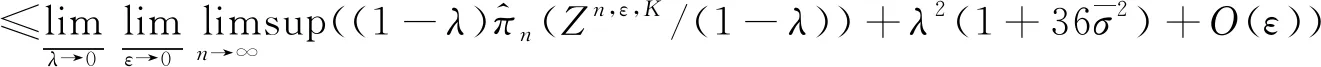




3 比较分析





4 结语

