初中数学核心素养的生成机制与培养路径研究

魏爱文

摘 要：如今，数学核心素养已经成为初中生数学教育的一个热门话题，核心素养的目标是将以人为本的教育理念扎扎实实地落实到教学中。数学学科核心素养作为数学课程三维目标体系的优化内容，是数学课程改革下的产物。为了保证数学新课程改革的高质量开展，学生数学核心素养的培养必须从理论转为实践，在转化伊始，教师必须整体明确初中数学核心素养的生成机制，并结合理论内容指导实践，探索出培养学生数学学科核心素养的有效路径。对此，本文将从数学核心素养培养出发，对上述两大问题予以深化探讨。

关键词：核心素养；数学教育；生成机制

【中图分类号】G633.6            【文献标识码】A             【文章编号】1005-8877（2022）22-0111-04

Research on the generation mechanism and cultivation path of mathematical core literacy in junior middle schools

WEI Aiwen （Huating Huangfu School， Pingliang City， Gansu Province， China）

【Abstract】Nowadays， the core literacy of mathematics has become a hot topic in mathematics education for junior high school students. The goal of core literacy is to implement the people-oriented educational concept into teaching. As the optimized content of the three-dimensional objective system of mathematics curriculum， the core literacy of mathematics is the product of the reform of mathematics curriculum. In order to ensure the high-quality development of the new mathematics curriculum reform， the cultivation of students' mathematical core literacy must be transformed from theory to practice. At the beginning of the transformation， teachers must clarify the formation mechanism of junior high school mathematics core literacy as a whole， and combine theoretical content to guide practice to explore an effective path for cultivating students' core competencies in mathematics. In this regard， this article will start from the cultivation of mathematical core literacy， and further discuss the above two problems.

【Keywords】Core literacy; Mathematics education; Generation mechanism

1.初中數学核心素养的生成机制研究

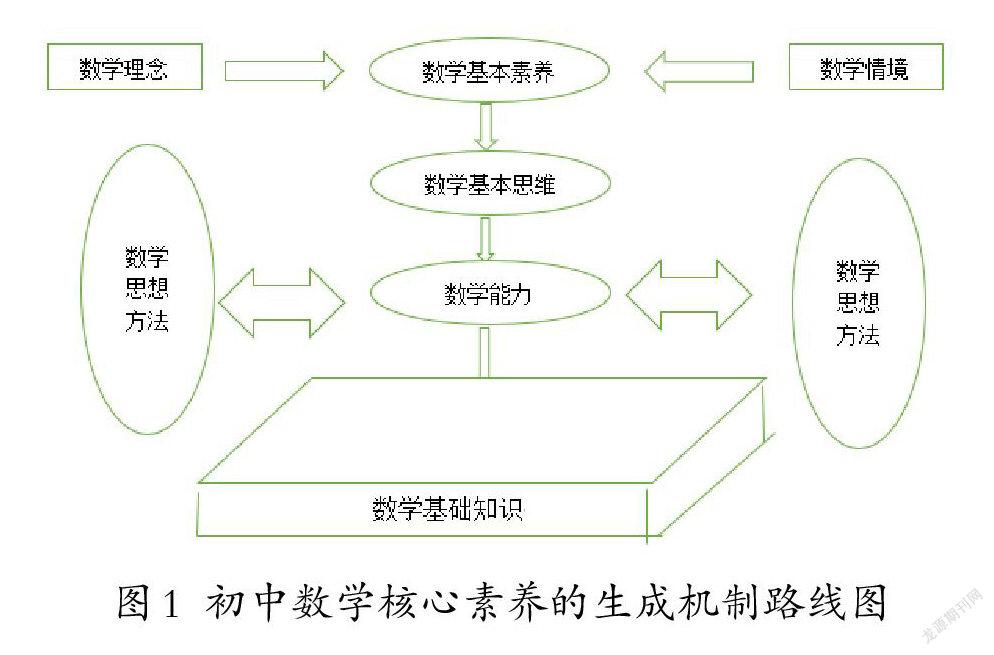
学者金吾伦在知识生成论中认为，知识的本质是生成，而非构成，且必须在整体框架内，才满足知识生成的特点。换言之，知识生成需要各基本知识点相互关联、转化及变体等各种整合方法而得到，而不是传统理念认为的不同知识点在未经变体后相互结合而成的。有学者针对知识生成论，结合数学教学，提出了言简意赅的核心素养总结：知识是能力产生的本源，那么数学知识即为数学素养生成的本源。结合知识生成论与数学核心素养的四大要求：数学基本素养、数学基本思维、数学能力、数学基本技能，可归纳出初中数学核心素养的生成机制路线图，见图1。

从图1中可以看出，所建构的生成机制路线图虽在逻辑层面上自洽有所不足，但从数学核心素养角度理解，具备关注数学学习情境化特点及数学理念的渗透性特点。具体生成机制可按照如下角度理解。

（1）数学学习情境化的生成机制体现

情境化即教学中需贴近日常生活，参考《义务教育数学课程标准（2011版）》对学生数学能力培养的目标，其中提及基本活动经验，涉及有关数学情境方面的内容。在PISA数学素养测试中，也强调要重视数学与日常生活的练习，不固化数学学习的思路，将数学思维运用到日常生活中，将思维迁移至其他学科的学习中。可见，教育学界一致认为数学学习情境化的生成体现为学生素养培养的重要一环，在教学设计中应将此元素贯穿于数学素养培养的始终。

（2）数学理念的渗透性生成机制体现

数学理念包括学生对数学学习的情感态度、数学思维、数学能力、数学技能、数学知识等内容。有具体案例研究结果表明，学生数学理念水平高低，能在一定程度上影响学生的数学成绩；另有调查显示，学生的外部学习动机远不如内部学习动机对学生数学成绩的影响。可见，在教学设计中，应提升学生对数学学习的情感态度、数学学习的主观驱动力、对数学的敬畏情感的培养，同步强化学生数学学习的内外部学习动机。

2.数学教学中学生核心素养的具体体现

（1）數学基础知识与基本技能教学体现

以初中数学方程为例，具体体现方面如下：第一，能将代数式、方程、等式的区别与共性；第二，能正确理解“方程”的意思，并可将一元一次方程、二元一次方程、三元一次方程降级转化；第三，能根据方程形式的不同，选择最适配的方程恒等变形步骤，并始终保持方程的解不变；第四，能正确理解分式方程一定要验根的理由，舍弃解的过程中方程两边是否恒等。方程的解与解方程细分属于两大知识领域，方程的解属于陈述性基础知识，此类基础知识学习无明确技巧，但知识点必须牢记；解方程属于基本技能，技能培养过程中教学方式不同，教学效果也不同，但最终目标在于增强学生的推理能力、运算能力及列方程解应用题的能力。

（2）数学学习综合能力表现

数学方程学习对学生推理能力及运算能力要求较高，需要学生掌握一定的运算规则，借助正确的运算形式，应用正确方式推理出方程的解。推理过程中融合运算过程，运算过程更包含推理的过程，属于对学生运算能力及推理能力的横向整合。但仍需注意的是，求解方程的过程中，数学能力的获得离不开学生对数学知识的使用，结合运算律相关的数学知识运动可强化学生的数学基础知识，可见数学学习综合能力表现与数学“双基”能力层间存在着纵向整合特点。具体体现方面如下：第一，方程求解时，能将方程最简化，转化中预测方程解的个数及方程解的性质，使学生认识到解方程实际上也为推理的过程；第二，能从问题情境提炼出核心问题，正确建模与设置变量，分析情境中的数量关系，考虑所架构模型的合理性，并且能熟练地解方程；第三，能将其他学科涉及数学思想部分的公式进行变形。例如，将物理学中的Q=cm△t变形为c=Q/m（△t）以突出所研究的比热容这一量，扩宽学生的问题思考路径，增强数学学习的灵活性。

（3）顶端能力架构，数学思维能力的表现

第一，具备将应用题目抽象化转换，以数学模型，方程思想的形式表达的能力。第二，具备列举范例，反驳问题的能力，例如，判断a1，a2，b1，b2，c1，c2为非零实数，[a1x+b1y=c1a2x+b2y=c2]是关于X，Y的二元一次方程组，问该方程组是否有解。这类题目属于逆向思维判断类题目，与常规解二元一次方程方式有所不同，为事先设想出答案，随后对所推断答案进行验证的一类题目。解决类似问题时，学生需列举出一个相反的例子，即可回答类似问题，对学生高阶思维能力也是一种锻炼，这种思维方式也可以迁移至其他理科学科如物理、化学中。第三，借助数学知识学习，锻炼自身分析问题、解决问题相对稳定的思维习惯。在理解方程性质推论、方程模型运用及方程概念求解的过程中，学生需通过内化、体验、辨别等形式逐步养成程序化、规范化及灵活化求解问题的能力。当然，在培养学生数学思维能力的过程中，仍要调动学生对数学的积极情感态度，同时需提升对问题情境抽象化理解的能力，进而转化为自身数学学习的核心素养。

3.初中数学核心素养的培养路径探析

（1）以全局化视角规划数学课程的开展

首先，教师从确立教学目标、教学情境、教学评价三阶段中，均需从教学实际出发，结合已经过论证的教学成果，从数学课堂教学全过程中，实施数学课堂教学。其次，需关注学生对课程知识的理解，授课过程中，可适当对授课内容进行深化，教材往往以精炼、简洁的语言呈现知识，虽然最终知识结果能清晰呈现，但忽略了知识推导的思维过程。教师可通过跨单元、单元、大单元、课时等途径实施教学，对教学内容及知识点做全局整合，回顾性分析所学知识，对碎片化且相对抽象难以理解的知识点在整体设计的同时，做分步整合，整体教学目标不限，将知识点以知识团的形式表达。例如，在一元二次方程、二元一次方程组、一元一次方程教学中，基础概念为方程，各环节教学则依靠解决实际问题的形式间接引出。有教学研究表明，在二元一次方程组的单元教学中，可利用总-分-总的教学形式，在整体复习知识点后，对具体细化知识点详细讲解，对其中所包含的解题思想做全局化总结，利于提升学生的知识迁移能力及自主探究意识，培养高阶数学思维。从实践中来看，日常教学实践中是培养学生数学素养的最佳时机，教学中结合数学学习者的学习方向，基于学科整体的知识框架及数学知识呈现的整体脉络开展教学，凸显清晰的教学方向。最后，以教学大纲为指引，注重培养学生高阶数学能力。初中方程学习中，尤为重视学生的数学建模思想培养，该领域知识来源于科技情境、生活情境、文化情境等实际情境，是学生提升建模能力的有效举措。例如，学生在学生学习过程中，自觉将数学问题与实际问题相结合，并做相互转换，列举出所构建模型，算出方程的“解”。验证结果时若结果不符合实际则需要转换模型，从其他思路思考问题解决的过程，直至得到满足实际需求的结果。

（2）创设合理的数学问题解答情境

数学核心素养强调学生对数学知识的理解与运用，但教学中不仅局限于数学技能与数学知识的教学，而在于引导学生在解决数学问题时学会同一类型数学问题的解决方式，如何利用所学知识、生活经验及数学推理等手段快速解决问题。例如，以信息技术为手段，将数学知识动态化呈现；从数学实验或数学探究活动出发，创设活动性情境，将数学知识以实践性的形式呈现；从数学故事及数学史出发，将数学知识以趣味化的形式呈现；在不同的知识点呈现情境中，需注重培养学生的交流、推理及数学思考能力，运用实际的问题呈现情境，可更好地促进学生对知识点的理解，提升教学效果。此外，也可让学生自创问题情境，给学生充分的思考空间。例如，自编一道应用题，并列举方程，使其解为x=3。此方式下评价学生数学素养，充分基于真实情境，相较于传统考查公式识记程度的方式，对学生数学素养的评价则更为透彻。准确的评价结果将作为后续教学方向的指引。可见问题情境是培养学生数学素养的基础路径，真实情境与任务的介入是学生数学素养培养的必经路径。但仍需注意的是，问题解决时，应以真实情境中某类问题解题过程中所获得的方法为解题核心，但这其中所指的方法并非解决某类问题时所采用的技能、具体技能及微观方式。如教学实例：构造全等三角形的辅助线具备一定技巧，这样的方式虽然针对性较强，但适用于的情境相对狭窄，不具有普适性，学生学过后容易遗忘。教师要明确传授给学生的解题模式应是具备普适性、可检验的、可迁移、宏观的解题模式，例如，韦达定理、配方法、因式分解法等，这些方法是可以帮助学生培养数学学科核心素养的。学生在解决问题时，不应仅仅将既往所学知识点的规则进行浅显应用，需要在解题过程中将已有的知识、原理及概念加以整合，并与情境中的问题相匹配。

（3）数学理念在日常教学中的渗透

长期以来，我國对初中学生数学学习效果评价注重的是数学内容与数学知识的掌握程度，仅以数学卷面成绩评价学生数学学习效果，导致数学理念在日常教学中的渗透缺乏客观性。为了解决这一问题，教学中不仅要注意培养学生数学基础知识与技能，也要关注学生数学学习中数学学习观及数学观等数学理念。实践教学中，可通过安排数学主题活动，加强学生数学情感、价值观及数学态度的正确引领，使学生树立学好数学、用好数学、爱学数学的自信。日常教学中也可通过小组问题讨论，共同研讨数学问题的形式，侧面提升学生的数学素养，深入探究学生外在能力与内在品质相关的能力。内容应涵盖数据分析、数学运算、直观想象、数学建模、逻辑推理与数学抽象等领域。以解决函数题目为例，不同学生对知识思想的理解深度有所差异，此方面属于外在能力范畴；对知识理解水平的不同，将导致解题思路、解题简便性水平及解题速度出现异同，此方面属于内在能力范畴，学生在技能知识运用同时，也可进一步理解知识的本质，透彻理解知识中所包含的数学思想。

4.关于数学核心素养的研究

根据相关研究，核心素养目前在国内可检索到的文章达到两千多篇，在过去，人们对核心素养并不关注，从2014年开始到现在，关于核心素养的相关文献越来越多。通过相关文献的分析，核心素养的培养对学生的学习非常重要。初中数学核心素养主要包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等六个方面。

5.提高初中学生数学核心素养的教学方式

（1）注重培养学生的抽象思维

为了提升初中数学教学效果，教师在开展数学课教学时，可通过构建思维导图和知识体系结构全面提升学生的抽象素养。例如，在学习了函数后，还需要拓展。学生的接受能力不同，有的学生抽象思维较差，无法理解抽象概念，例如，对二次函数模型的认识不够深刻，有时会出现混淆。在上复习课时，有必要对相关的知识点进行归纳、整理和概括，构建初中数学知识体系结构图。在教学中，教师应该充分利用多媒体的优势，把有关的数学知识点提炼出来，通过思维导图或者知识结构图的形式加以归纳，解决知识碎片化问题，重建学生的数学知识体系结构，重塑学生的思维品质，提升学生的抽象素养。

（2）注重培养学生的逻辑思维

从当前来看，逻辑思维在一些新题型和新型应用题上体现得越来越明显，目前初中数学教学中，教师首先应该培养学生的核心素养，以逻辑思维为基础，提高学生的思维拓展。在考试中，有些题目一方面是考查数学水平，另一方面也是在考查学生的数学创新能力和理解能力，从侧面体现出一个学生对数学题目的理解和解题思维。元认知下的数学思维是从理解和创新、逻辑等多方面考查学生的数学水平。综上原因，核心素养下学生逻辑思维的培养至关重要。

（3）注重培养学生的建模能力

注重对学生建模意识的培养。例如题目中所述：若干名学生，若干间宿舍，若每间住4人将有20人无法安排住处；若每间住8人，则有一间宿舍的人不空也不满，问学生有多少人？宿舍有几间？此时可应用建模思想解题。可设宿舍共有x间，那么根据题意可知8（x-1）<4x+20<8x，得出5

（4）注重培养学生的数学运算能力

首先，教师应展示完整运算步骤。例如在进行一元一次不等式的讲解时，教师应当在课上对各个解题环节充分进行讲解，完整展示解题步骤，避免学生在后续运算中形成固化思维，出现运算错误。其次，要详细区分运算知识的关联，培养学生养成良好的运算习惯，仔细审题，规范答题格式，提升学生运算书写的规范性水平。再次，要培养学生的归纳能力，教会总结问题共性，举一反三，提升学习效率。

（5）注重培养学生的直观想象能力

在教学中，教师应巧妙运用教材资源，合理设计教学过程。以七年级上册“几何图形”这一讲解内容为例。教师授课前准备好由小立方块组成的立方体。随后让学生分别从正面、左面、上面三个角度去观察立方体。随后利用数学模具，将学生的观察能力一步步转化为对所学知识点的深入理解。也可让学生将所观察到的图形绘制于纸上，学生在脑海中构思立方体的结构，最终将所思所想展现于纸上，促使其对数学中抽象的问题进行简单化理解，进而培养学生的想象能力。

（6）注重培养学生的数据分析能力

在初中数学教学中，有些简单的内容经常会产生较高的错误率，例如，集合问题是目前在数学概念中应用最为广泛的一种，在考试过程中，常常会出选择题和填空题来考查学生对知识的掌握程度。填空题与选择题不同于大题目和应用题，要求学生既要快速又要准确地算出答案，所以学生掌握合适的解题方法和解题思路是非常重要的。例如，在做选择题以及填空题时，可以采用数形结合的方式进行数据分析，充分掌握解题思路以及技巧，才能做到又快又准确。对于集合问题，元认知是将数量之间的关系进行合理的整理、梳理，将每一组数据进行综合分析后，以图形的形式体现出来，最终找到答案。对于方程式和不等式的求解问题，元认知下的数学方法同样适用。求解方程和不等式的题目，在初中数学考试中极其普遍范围又广，方程式又分为很多种，如二次方程，一元二次方程等。将其规划成不同的类型，但是在解题过程中，无论什么样的方程式都可以合理巧妙地运用数学方法进行解题，比如，在构建函数之后，可以画图分析，根据方程式所得出来的根，也就是两个函数图形在坐标系上的交点画图。

综上所述，数学素养不仅外显于能力方面，也内显于思维品质方面，最终内化为学生的数学学习观，学生数学素养的培养可以从日常教学角度出发，以思维、能力、技能、数学知识的获得途径来实现。在日常教学中数学素养的培养应从三方面展开，包括数学理念在日常教学中的渗透、创设合理的数学问题解答情境及以全局化视角规划数学课程，这样不仅能提升学生的思维素养及数学能力，也可提升教师的授课质量。

参考文献

[1]王焕.浅析初中数学核心素养的培养路径[J].读与写，2021（05）.