基于EBSBL-BO算法的L-DACS系统干扰抑制方法

李冬霞 王雪 刘海涛 王磊

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

1 引言

L 频段数字航空通信系统（L-band digital aviation communication system，L-DACS）是未来面向航路飞行阶段的空地数据链路［1］，它采用正交频分复用（orthogonal frequency-division multiplexing，OFDM）调制［2］，有效频带宽度为0.5 MHz，主要为飞机与地面管制中心、航空公司之间提供数据交换服务［3］。L-DACS 系统内嵌于DME 系统的工作频段之间，因此两系统的信号工作频带存在部分交叠。且DME信号发射功率远超过L-DACS 系统的发射功率，造成L-DACS系统OFDM接收机性能急剧恶化［4］。

关于上述问题，国内外研究者从不同角度开展了多种DME 信号干扰抑制方法研究［5］，大致分为以下三类：（1）非线性干扰抑制方法。该类方法的典型代表为脉冲熄灭、脉冲限幅［6］，其工作机理是：当接收机接收信号的幅值超过规定的阈值时，认为受到脉冲信号干扰影响，此时将信号幅值设定为门限值，达到干扰抑制的目的。这种方法具有阈值设定困难、易产生子载波间干扰等问题［7-8］。（2）基于空域滤波的干扰抑制方法。该类方法利用信号空域到达方向不同，通过波束形成实现干扰消除［9-10］；存在的主要问题是接收机需要安装阵列天线、运算复杂，应用范围受限［11］。（3）基于DME信号模型重构的干扰抑制方法［12］。该类方法主要是利用OFDM 空子载波不传输有用信息的条件，重构DME干扰信号，并将其从接收信号中去除。最具代表性的是基于压缩感知理论重构DME 干扰信号。文献［13］运用DME 信号的稀疏特征，通过两级滤波与压缩感知算法进行DME信号重构，进行干扰抑制，虽然干扰抑制效果良好，但仍存在着一定的重构误差。文献［14］提出基于稀疏贝叶斯学习（Sparse Bayesian Learning，SBL）算法的信号重构方法，该方法将电力线系统中的脉冲信号视为稀疏信号进行重构。相比于其他重构算法，该算法适用范围更广，即使不知道信号的分布特点，重构的效果依旧比较好，但是该算法运算复杂度较高，运算时间较长。由于DME信号并不是完全稀疏的，因此目前使用的SBL 算法存在一定的重构误差。

文献［15］提出了块稀疏贝叶斯学习（Block Sparse Bayesian Learning，BSBL）算法，无论信号是否稀疏该算法都适用。基于此，文献［16］提出了一种基于耦合稀疏贝叶斯（Pattern Coupled Sparse Bayesian Learning，PC-SBL）的信号重构方法，该方法利用耦合系数来控制块稀疏信号之间的相关性，该算法虽然运算时间短，但是重构精度低。文献［17］根据信号分块信息是否已知，进一步派生出边界优化BSBL（BSBL-the bound optimitation，BSBLBO）算法和扩展边界优化BSBL（expanded BSBLBO，EBSBL-BO）两种算法，无论信号是否稀疏都能够达到较好的恢复效果。文献［18］在假设分块信息已知的条件下，利用BSBL-BO 算法实现DME 脉冲信号重构并消除，取得了较好的脉冲干扰抑制效果；而在实际运行系统中，DME 信号出现的时间以及位置往往是未知的，即分块信息未知。

为应对信号分块未知的情景，本文提出了基于EBSBL-BO 的DME 干扰抑制算法。其基本思想是：利用接收信号的空子载波构建压缩感知模型，考虑任意情形的DME 信号分块结构，根据EBSBL-BO 算法将DME信号进行重构，并在时域消除。在相同仿真环境下，与其他干扰抑制算法进行对比后，发现本文算法误码率更低，性能更优。

2 系统模型

2.1 DME脉冲信号模型

按照国际民航组织附件10 的规定，单个DME脉冲对的形式如下［19］：

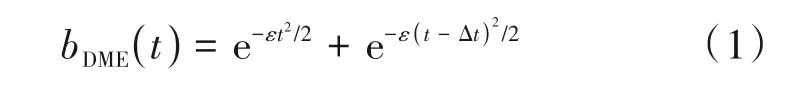
上式中，ε=4.5 × 1011s-2；Δt为脉冲之间的时间间隔，取值与DME基站的传输模式有关。

DME发射信号与L-DACS系统正交频分复用接收机有0.5 MHz 的频率偏移，需要考虑载波偏置对L-DACS 系统的影响。单一DME 信号源时，其脉冲信号建模为：

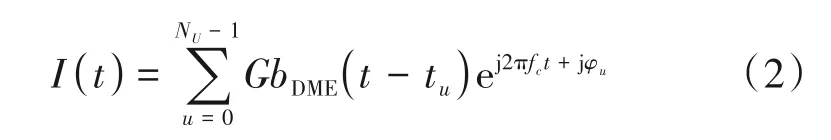
其中，NU为观测时间内的总脉冲对数；G为信号峰值幅度；fc为频偏值；u为脉冲对的序号；φu表示第u个脉冲对的载波信号起始相位，在[0，2π]范围内服从均匀分布；tu表示第u个脉冲对出现的时刻，服从泊松分布。

2.2 L-DACS系统发射机

L-DACS 系统发射机由卷积编码、交织、调制、上采样、D/A 转换等功能模块组成，如图1 所示。其中，调制模块可采用正交振幅调制、正交相移键控等调制方式，调制后信号映射到发射机的N个子载波上。接着进行采样因子为V的上采样，再通过VN点IFFT 转换为时域信号x。最后，插入循环前缀，经D/A转换和射频前端处理后发射。

图1 L-DACS系统发射机Fig.1 L-DACS system transmitter

2.3 L-DACS系统接收机

图2 为基于EBSBL-BO 算法的L-DACS 系统接收机。假设接收端定时同步与载波频率补偿已经建立，经天线接收到的射频信号经过干扰抑制前处理，干扰抑制处理以及干扰抑制后处理三个过程，最终输出比特序列。

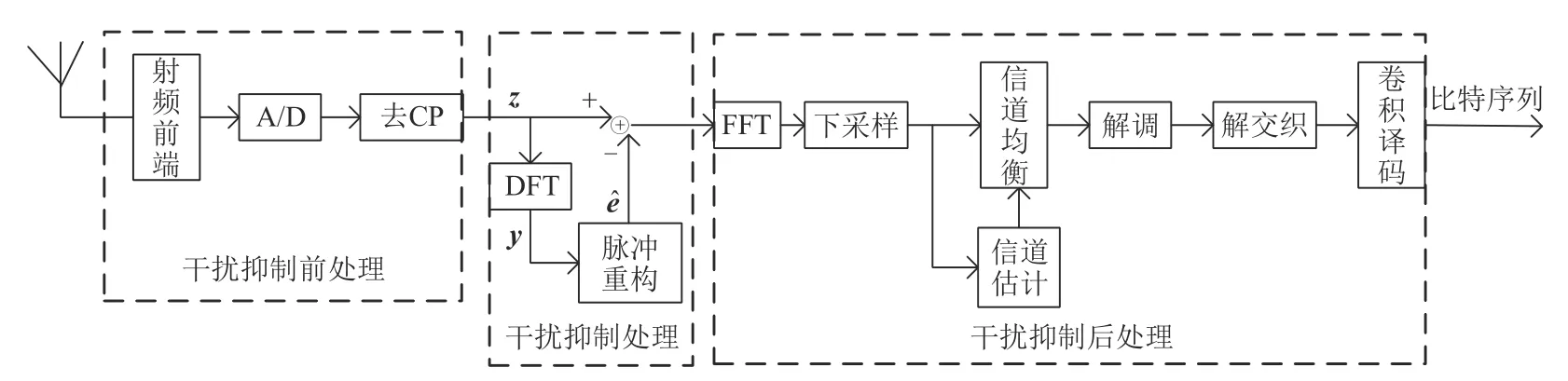
图2 L-DACS系统接收机Fig.2 L-DACS system receiver

接收信号进行干扰抑制前处理后，得到的时域信号矢量为：

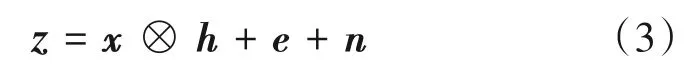
式中，x为发送的OFDM 时域信号矢量；⊗表示卷积；h为信道脉冲响应；e为接收到的DME 信号；n为白噪声。

为了重构DME 干扰信号，首先对接收信号z进行傅里叶变换得到：

式中，v≜Dn是n的频域矢量，满足为离散傅里叶变换矩阵；X=Dx为OFDM 信号的频域形式。

OFDM 系统中有M个空子载波，(·)k表示空子载波所在位置对应的子矩阵（或子向量），则xk=0。以下利用空子载波构造压缩感知信号模型。将xk=0，代入到式（4）中则有：

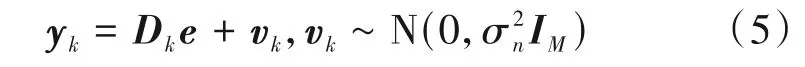
式（5）是一个标准的压缩感知线性回归模型［20］。其中，yk∈RM×1为对应空子载波集合的观测向量为感知矩阵，为矩阵D的子矩阵；e∈RVN×1为待重构的干扰信号矢量；vk∈RM×1为白噪声。

利用EBSBL-BO 算法重构DME 脉冲信号，重构出的DME 干扰信号记为，并从接收信号z中去除。干扰抑制后的信号，进一步经过信道估计和解调，最终输出比特序列。

3 基于EBSBL-BO 算法的DME 脉冲干扰抑制

3.1 算法描述

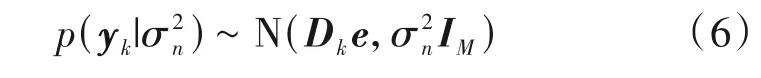
假设脉冲信号e具有块结构，且各个分块长度固定为d。由于具体的分块信息未知，可认为信号e具体分为g个信号块，第i个信号块表示为e（ii=1，2，…，g），则最大块数量为gmax=VN-d+1：

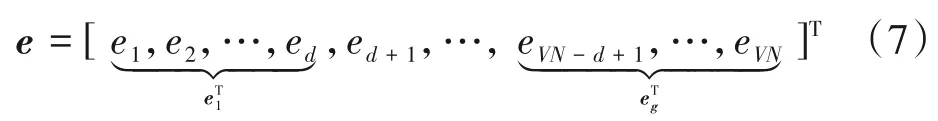
在g个块中，有且只有s块（s≤g）是非零的，其实际位置未知。

假设每个信号块ei∈Rd×1满足多变量高斯分布：

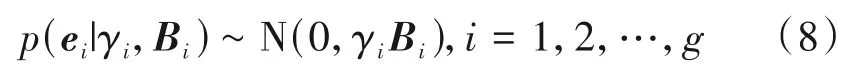
其中，γi是非负标量，用来控制信号e中非零块的分布，当γi=0时，第i个信号块是全零值；Bi是正定矩阵，代表第i个信号块内的相关性。进一步假设信号块之间不相关，则有：

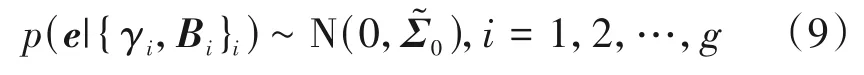
根据分块情况，对信号e进行如下分解：

参考式（8）和式（9）的概率密度表示形式，可推导得到信号u的后验概率分布：

其中，μu表示均值；Σu表示协方差。

3.2 参数估计

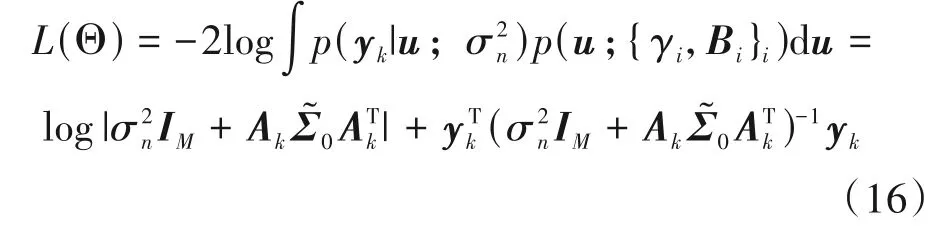
计算L(Θ)关于和Bi的导数，并使其导数为0，可以得到和Bi的学习规则为：

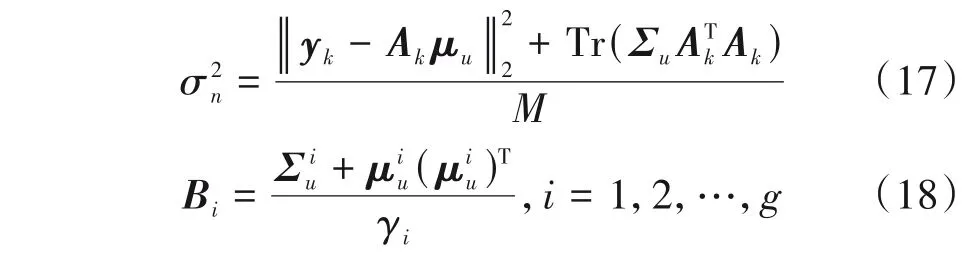
考虑到分块长度相同，为了避免过拟合，令Bi=B(∀i)。利用此约束条件，可以得到B的更新表达式为：

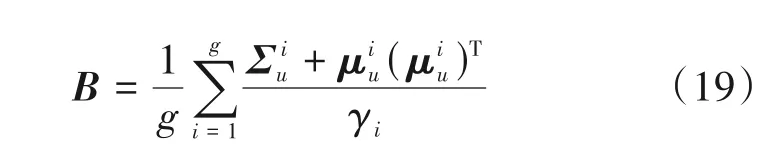
为进一步优化算法性能，构造一个接近矩阵B的正定对称矩阵，使其组成元素由一个参数决定，形式如下：

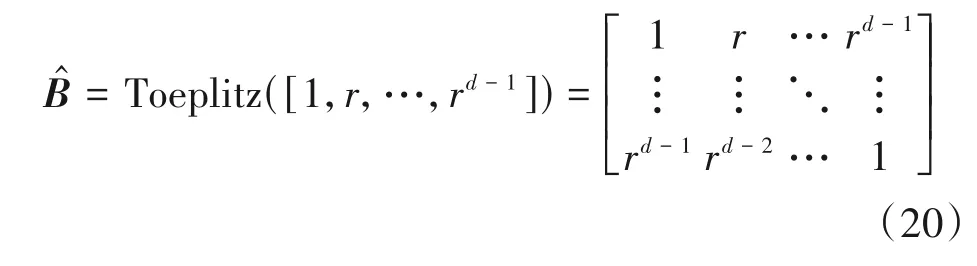
其中，r为一阶自回归系数分别为矩阵B中主对角线与次对角线上的元素均值。

γi的估计按照BSBL-BO 算法［15］，将式（16）中的代价函数优化后，求导得到参数γi的更新表达式为：

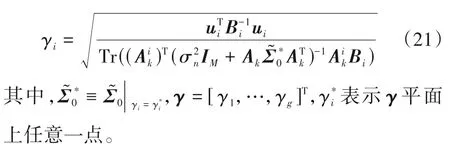
综上所述，式（17）、（20）和（21）即为EBSBL-BO算法中所求参数、Bi和γi的更新表达式。EBSBLBO算法主要流程如下：

3.3 算法复杂度分析

本文所用EBSBL-BO 算法的运算复杂度主要由三部分决定：待重构信号的均值、协方差和估计参数。根据公式（14）、（15）、（21），其运算复杂度分别为O(M(dg)2)、O(M(dg)2+M3)和O(dg)。因此在每次迭代运算中，EBSBL-BO算法的复杂度为O(M(dg)2+M3+dg)。在算法应用中dg≥VN＞M，因此EBSBLBO算法的复杂度为O(M(dg)2)，与BSBL-BO算法相较，本文算法复杂度略高，但在实际应用时，由于本文独特的分块结构，使得EBSBL-BO 算法收敛速度快，所需的迭代次数远小于BSBL-BO 算法，因此EBSBL-BO 算法有更高的运算效率。表1 给出了几种算法的运算复杂度对比。

表1 算法的运算复杂度Tab.1 Computation complexity of algorithms

4 仿真分析

4.1 仿真参数设置

为验证本文算法的有效性，本文搭建了基于EBSBL-BO 算法的DME 干扰抑制仿真验证系统。分别从DME 信号重构误差、系统功率谱变化、接收信号星座图以及误码率几个维度进行仿真分析与验证，并与SBL算法、PC-SBL算法、BSBL-BO 算法进行了性能对比，验证本文方法的抑制效果。表2 为仿真系统的技术参数配置。

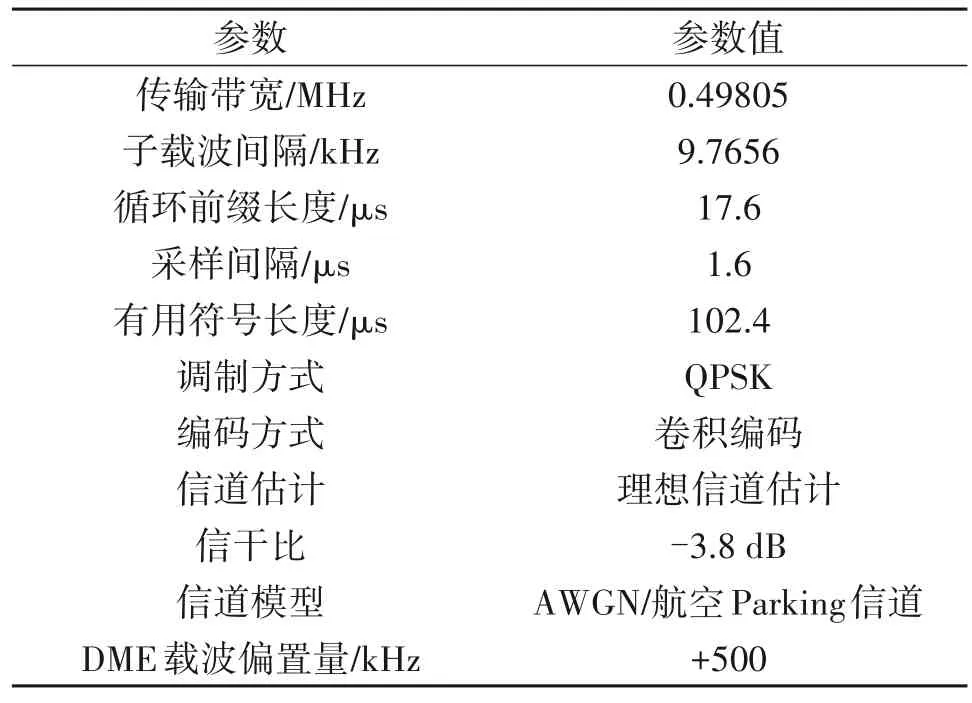
表2 仿真参数Tab.2 Simulation parameters

4.2 DME脉冲信号重构效果

图3为基于EBSBL-BO算法重构前后DME信号时域波形。其中，图3（a）、3（b）分别为原始DME 信号波形、使用本文方法恢复得到的DME 脉冲波形。对比图3 发现：重构信号的波形幅度以及位置与原始信号几乎一致，证明EBSBL-BO 算法可以有效恢复DME信号。

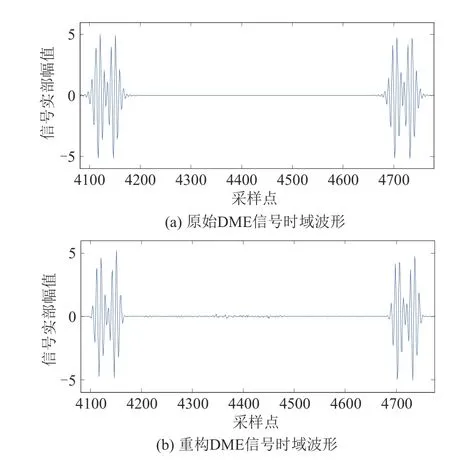
图3 DME信号重构效果图Fig.3 Reconstruction effect diagram of DME signal

图4为使用不同信号重构算法得到的归一化均方误差曲线。显示了DME 脉冲信号重构的归一化均方误差随信噪比变化规律。观察可知：（1）随信噪比的增加，均方误差在逐步减小，说明信噪比越高，重构效果越好。（2）信噪比相同时，本文算法重构误差最小，本文算法相较于SBL 算法有7 dB 的性能改善，相较于BSBL-BO 算法有2 dB 的性能改善，证明本文算法重构效果最优。

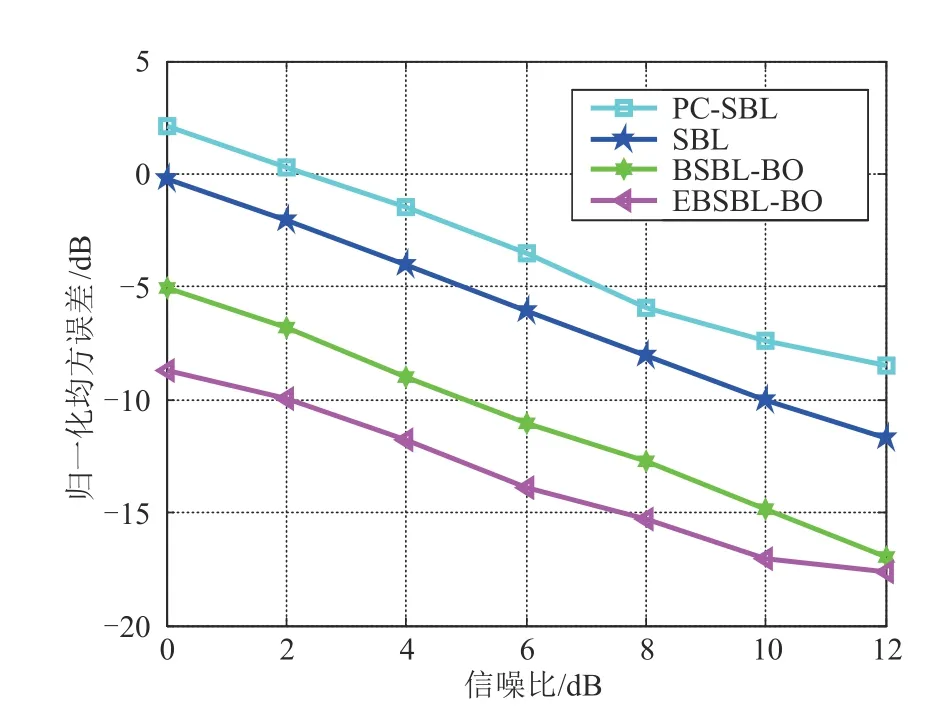
图4 DME信号重构误差（归一化）Fig.4 DME signal reconstruction error（normalized）

4.3 DME脉冲干扰抑制效果

图5 为不同阶段OFDM 信号的功率谱对比图。图5（a）、5（c）分别为发射与接收端OFDM 信号功率谱，对比两图可以看出：在0.25 MHz 处接收信号中有明显的DME 干扰频率分量；图5（b）为滤波后的DME 信号功率谱，可以看出滤波后DME 信号功率在0.25 MHz 依旧高达-20 dBw；图5（d）为本文算法干扰抑制后OFDM 信号功率谱，可以看出此时DME干扰分量明显被抑制，证明本文算法抑制干扰效果良好。

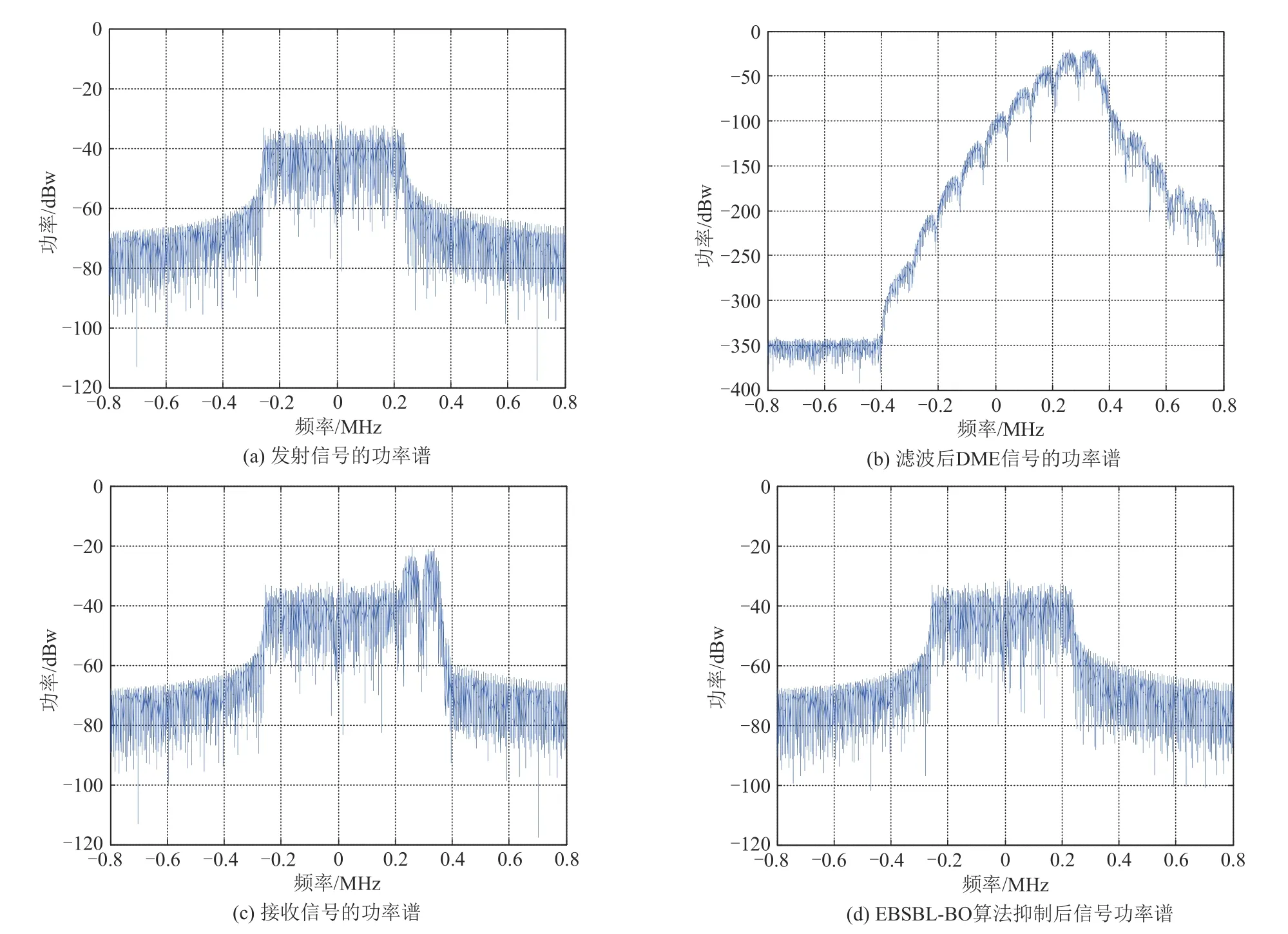
图5 系统信号功率谱对比Fig.5 Comparison of system signal power spectrum

4.4 不同算法接收信号星座图

图6显示给出了不同情况下接收信号的星座图对比。图6（a）显示：当没有高功率DME 脉冲干扰时接收信号星座图收敛完好；图6（b）显示：当存在高功率DME 脉冲干扰时接收信号的调制星座发散严重；图6（c）显示：经SBL 算法抑制后，接收信号的调制星座较为收敛；图6（d）显示：经EBSBL-BO 算法干扰抑制后，接收信号的调制星座相较于SBL 算法更为收敛，进一步证明本文所用EBSBL-BO 算法干扰抑制效果优于SBL 算法，但是与图6（a）相比，仍有部分残留干扰。

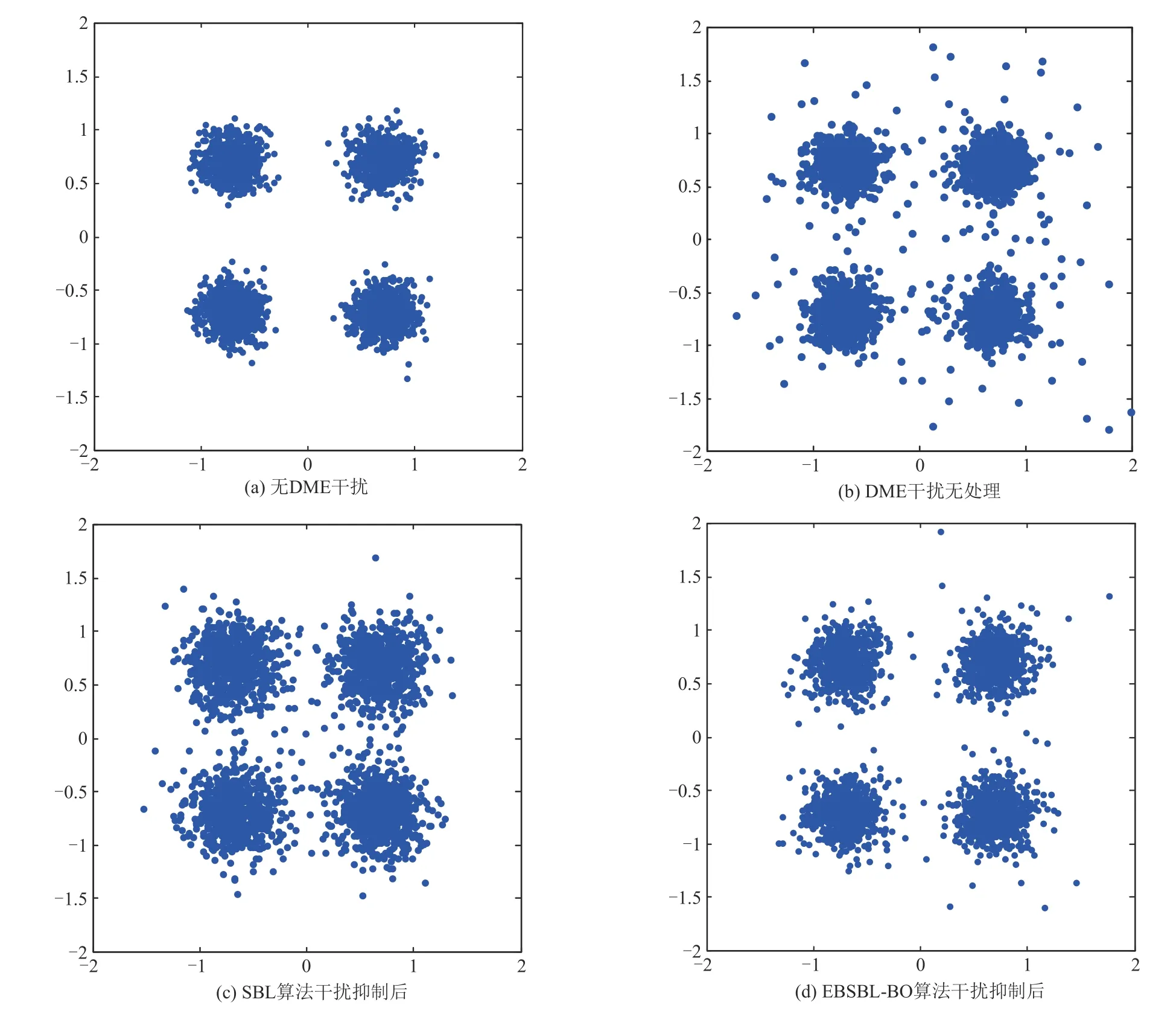
图6 接收信号星座图对比Fig.6 Receiving signal constellation diagram comparison

4.5 比特差错性能

图7 为AWGN 信道下的接收系统误比特率曲线。观察可知：（1）存在高功率DME 脉冲时系统的误比特率明显偏高，本文提出的干扰抑制方法在AWGN 信道下可有效降低系统误比特率，减轻DME脉冲干扰的影响；（2）与PC-SBL，SBL，BSBL-BO 三种干扰抑制算法相比，本文所用方法的抑制效果更优；（3）当误码率为10-3时，相较于PC-SBL 算法，本文方法有6 dB 的性能提升，相较于SBL 算法，本文算法有4 dB的性能提升。

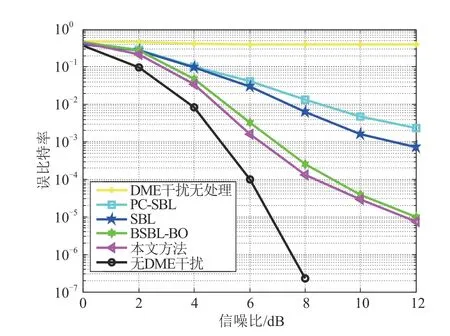
图7 AWGN信道下误比特率曲线Fig.7 Bit error performance curve under AWGN channel

图8 为多径信道下的接收系统误比特率曲线。观察可知：（1）本文提出的干扰抑制方法在多径信道环境下可以有效的减轻DME 脉冲干扰的影响；（2）与PC-SBL，SBL，BSBL-BO 三种干扰抑制算法相比，本文所用方法的抑制效果更优；（3）当误码率为10-2时，相较于PC-SBL 算法，本文方法有6 dB 的性能提升，相较于SBL 算法，本文算法有3 dB 的性能提升。

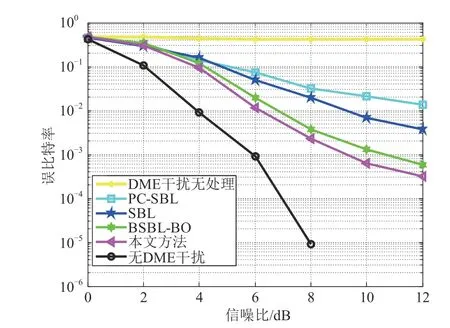
图8 多径信道下误比特率曲线Fig.8 Bit error performance curve under multipath channel

4.6 平均运行时间

图9 为AWGN 信道相同仿真环境下，四种DME脉冲干扰抑制方法的平均运行时间曲线对比图。对比可看出：运行时间最长的是SBL 算法，最短的是PC-SBL 算法，运行时间越短，收敛速度越快。EBSBL-BO 算法平均运行时间小于BSBL-BO 算法，收敛速度优于BSBL-BO算法。

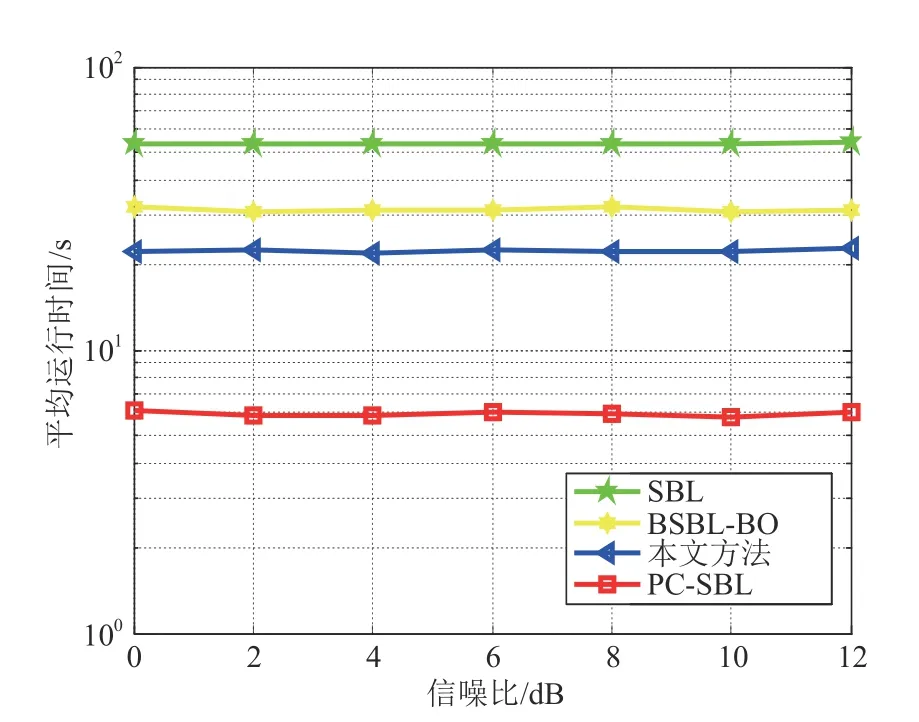
图9 平均运行时间对比Fig.9 Average running time comparison

5 结论

本文将DME信号建模为块稀疏干扰信号，并针对DME脉冲信号分块信息未知的情况，提出了基于EBSBL-BO 的DME 脉冲干扰抑制方法。首先利用空子载波构建压缩感知模型，然后利用EBSBL-BO算法重构DME 脉冲干扰信号，最后在时域进行消除，实现DME脉冲信号干扰抑制。通过仿真验证并与其他稀疏贝叶斯算法相比，发现本文算法重构效果更优，误码率更低，性能与收敛速度兼具。可有效提高L-DACS系统接收机性能。