铁路预应力混凝土矮塔斜拉桥索梁锚固构造选型与力学性能研究

马雅林,陈桂龙

(1.中铁二院工程集团有限责任公司,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

矮塔斜拉桥是一种介于梁桥与传统斜拉桥之间的新型桥梁结构，具有造价经济、结构合理、景观良好等优点，已被广泛应用于公路、铁路工程中[1-4]。作为矮塔斜拉桥传力体系的关键环节，索梁锚固结构受力较大且复杂，局部应力集中效应明显，极易发生开裂、破坏，进而导致桥梁整体结构的受力状态发生改变，严重影响正常使用功能[5-7]。

目前，针对铁路矮塔斜拉桥索梁锚固结构受力性能研究相对较少，主要集中于公路矮塔斜拉桥方面[8-11]。如周绪红等[12-13]通过有限元软件对索梁锚固区在最不利荷载组合作用下的受力性能进行研究，并对锚固区及钢箱主梁进行极限承载力分析；陈彦江等[14]通过足尺试验和数值模拟研究锚拉板式索梁锚固结构在设计荷载下的应力分布及传力机理，得到各受力区域在不同荷载等级下的应力分布情况；张少华[15]采用有限元联合仿真方法，模拟分析了矮塔斜拉桥索塔分丝管型索鞍锚固区鞍下混凝土的应力情况。由于使用上的要求不同，铁路斜拉桥与公路斜拉桥在力学要求上具有明显区别。铁路斜拉桥的桥梁宽度较公路斜拉桥更小，所承受的荷载中活载占总荷载比例更大，且活载集度大，动力效应明显[16-19]。在这种力学性质下，作为铁路斜拉桥主要受力结构的斜拉索与其对应的索梁锚固区受力状况就需格外重视。

基于此，以成昆铁路攀枝花金沙江大桥为依托，提出预应力矮塔斜拉桥索新型梁锚固形式—梁顶混凝土锚固结构，并采用ANSYS对比其与传统锚固结构的受力性能。在此基础上，根据相似理论设计并进行了缩尺模型试验，研究顶板锚固结构的实际应力分布及其控制因素，确认其在合理安全储备下的承载能力。

1 工程背景

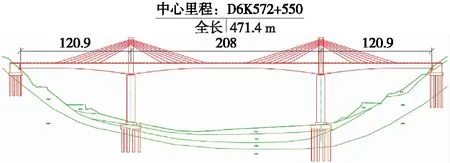
图1 攀枝花金沙江大桥孔跨布置(单位：m)

成昆铁路攀枝花金沙江大桥作为成昆铁路扩能改造的控制性工程之一，是我国第一座开建的跨度超过200 m的铁路预应力混凝土矮塔斜拉桥[20]。该桥为双塔预应力混凝土矮塔斜拉桥，塔高28 m，桥长471.30 m，共3跨，跨径组合为120 m+208 m+120 m，大桥设计桥面高程1 043.19 m，设计桥梁底缘高程1 029.83 m，如图1所示。主梁采用单箱双室变高度箱形截面，跨中及边支点处梁高13.1 m，中支点处梁高11.3 m，底板采用抛物线过渡为减弱索梁锚固结构受拉端与顶板相接处的拉应力，该桥索梁锚固区在设计中抛弃了铁路矮塔斜拉桥所普遍使用的翼缘下侧锚固结构，采用一种新型索梁锚固形式—梁顶混凝土锚固结构，如图2所示。

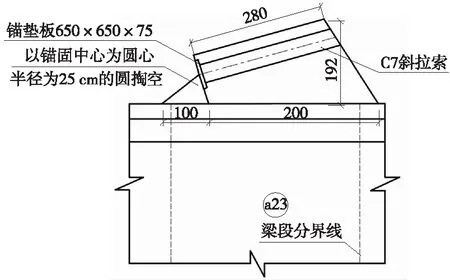
图2 新型梁顶混凝土锚固结构(单位：mm)

2 索梁锚固结构选型分析

通过ANSYS软件建立该索梁锚固结构的三维有限元模型，并与传统索梁锚固结构(翼缘下侧锚固结构)进行对比分析。其中，主梁为单箱双室箱梁结构，长24.96 m、底板宽10.60 m，顶板宽13.10 m，翼缘板宽1.55 m，腹板厚0.50 m，顶板与底板厚均为0.40 m，锚拉块宽0.80 m。模型具体材料参数见表1。设计索力为10 000 kN，二期荷载为19.5 kN/m2，集中力施加在索塔另一侧，Mz=675.114 kN·m，Nx=669 038.564 N，Qy=432 344.321 N。

表1 模型材料参数

图3为翼缘下侧锚固结构整体变形和各类应力云图。综合分析可知，翼缘下侧混凝土锚固块计算的整体变形为2.016 mm，3个方向的正应力及主拉应力(第一主应力)数值较大，其中，X方向局部应力达到8.82 MPa，其次为Y方向和Z方向，主拉应力约为9.89 MPa，超过混凝土抗拉强度。且峰值均集中出现在锚块与箱梁局部连接位置，造成局部混凝土开裂。这是由于索梁锚固块相对腹板形心存在偏心距，斜拉索受力后产生了较大偏心弯矩从而导致局部应力超限。

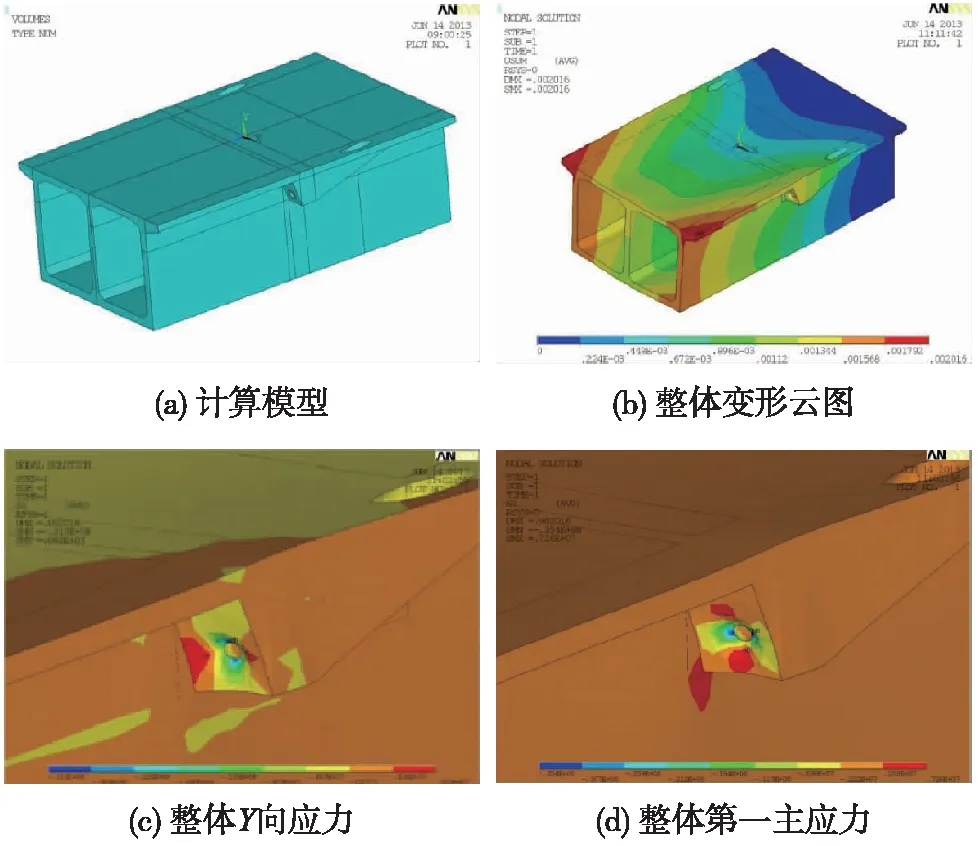
图3 翼缘下侧锚计算模型及计算结果

图4展示了梁顶混凝土锚固结构的应力云图，通过应力云图可以发现，梁顶混凝土锚固结构的受力显著减小。锚块Y方向(竖向)最大应力为4.07 MPa，由预应力钢束锚固点集中产生，采用锚垫板可分散应力集中现象。锚块ZS方向(纵桥向)最大应力为5.28 MPa，出现在拉索锚固点且范围较小，是由于在局部分析计算时，拉索内力完全施加在锚板上所致，实际构造中采用锚板加劲肋传递部分索力至锚块范围，可显著减小锚板处应力集中现象。锚块第一主应力为7.95 MPa，出现在锚板与楔形块导角处且范围较小，可通过设置整体承压钢板减小应力集中现象，满足TB 10002.1—2018《铁路桥涵设计基本规范》要求。

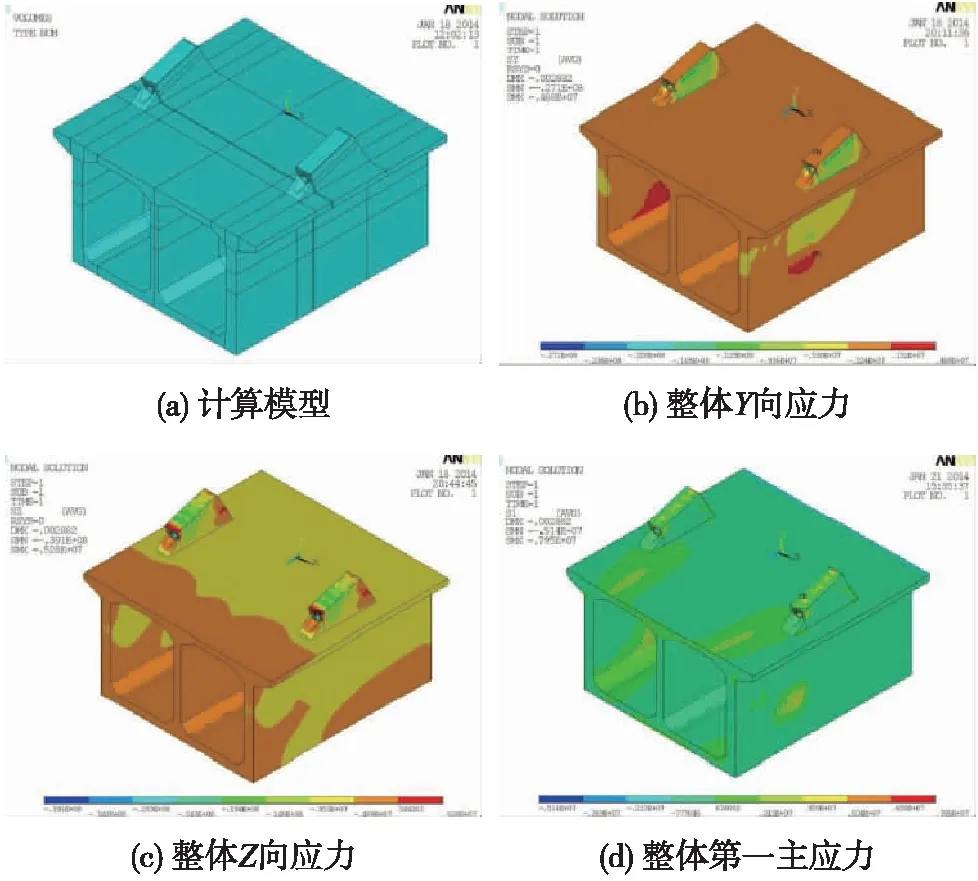
图4 梁顶混凝土锚块计算模型及计算结果(单位：MPa)

3 索梁锚固结构局部应力分析

3.1 模型试验介绍

为进一步分析梁顶混凝土锚固结构在荷载作用下各部位的应力水平及应力分布情况，以金沙江大桥的承受荷载最大索梁锚固区构件为原型，进行相似比为1∶2的模型试验。试验模型按照原型施工图纸进行设计、制作，如图5所示。根据相似理论[21]，锚固块长、宽、高为原型的0.5倍，任意截面钢筋总面积为原型的0.25倍，通过同时改变钢筋直径和钢筋间距来实现；钢束有效应力为原型0.25倍，在保证钢束规格不变的情况下，通过改变钢束束数和锚下张拉力来实现应力的缩放。

图5 试件制作完成效果

在试件养护完成开始试验，按每一级加载增量为设计最大索力的20%，加载至1.4倍最大设计索力，此后持续加载10 min，然后按每一级加载增量为设计最大索力的10%，加载至2.0倍最大设计索力。在正式加载过程中，每级加载到位后，记录构件的结构变形，检查测试仪器是否正常工作并记录数据。

3.2 试验结果分析

图6为不同工况下索力每级张拉持续作用5 min后，内埋式应变计测得的混凝土应变情况，可以看出，锚固块在不同张拉荷载作用下直至张拉至设计索力，其应变增幅基本上线性增加，卸载后同样呈线性减小，且各测点相对残余应变均小于20%，说明混凝土在线弹性阶段受力。在200%设计索力下，锚固块各部位的应变最大，最大拉应变出现在模型倒角处约为100.7，经换算为实测应力为3.6 MPa，并与理论应力对比见图7，可知受检构件试验截面各应变测点的实测应变值基本均小于其对应的理论计算值，且在规范和设计文件要求范围之内。

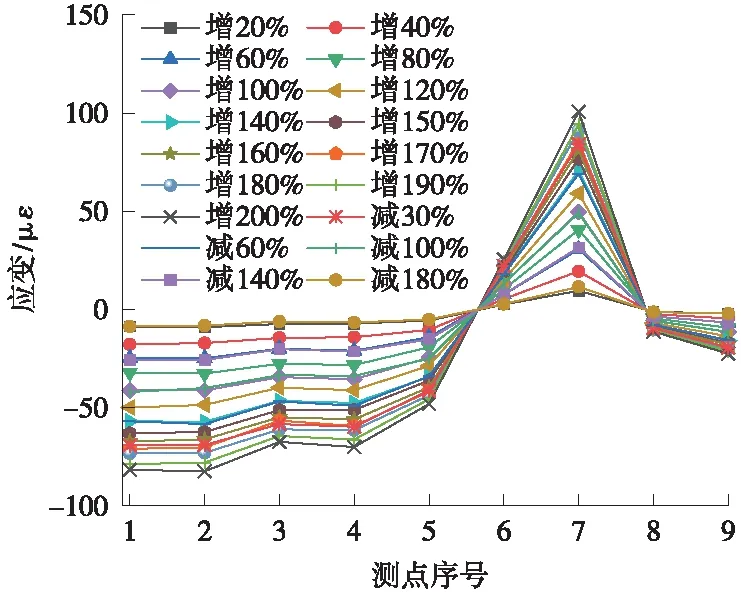
图6 锚固块实测应变值

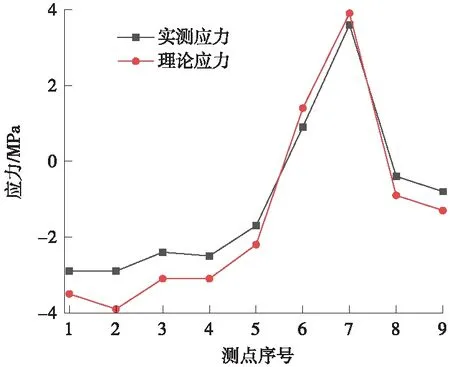
图7 应力实测值与理论值对比(200%设计索力)

此外，锚固块试验荷载加载至140%设计索力时，锚固块前端倒角位置开始出现的细小裂纹，随着荷载增加不断慢慢开展，宽0.3～0.4 mm，长约12 cm。另一侧也开始出现2条细小的斜裂缝，裂缝宽0.1～0.2 mm，长分别约16 cm和8 cm，见图8(a)。当荷载加载至170%倍设计索力时，之前出现的裂缝继续随着荷载增加不断开展，宽0.2～0.5 mm，长约22 cm。另一侧出现2条细小的斜裂缝，裂缝宽0.2～0.6 mm，长分别约25 cm和8 cm，见图8(b)。当荷载加载至200%倍设计索力时，之前出现的裂缝继续随着荷载增加不断开展，宽为0.6～0.8 mm，长约34 cm。另一侧出现2条细小的斜裂缝，裂缝宽0.6～0.8 mm，长度分别约30 cm和12 cm，见图8(c)。当荷载卸载至0时，之前出现的裂缝继续随着荷载减小不断闭合，宽度肉眼不可见，见图8(d)。

图8 模型裂缝开展

4 结论

依托攀枝花金沙江大桥，对铁路矮塔斜拉桥索梁锚固结构进行优化，并采用数值计算分析及模型试验研究，通过ANSYS软件建立三维有限元模型，对比梁顶混凝土锚固结构与翼缘下侧混凝土锚固结构的受力性能，计算得出Y方向(竖向)最大应力为4.07 MPa，由预应力钢束锚固点集中产生；锚块Z方向(纵桥向)最大应力为5.28 MPa，出现在拉索锚固点；锚块第一主应力为7.95 MPa，出现在锚板与楔形块导角处。可见梁顶混凝土锚固结构的各向应力指标均优于传统锚固结构。通过对梁顶混凝土锚固结构进行缩尺模型静载试验，该锚固结构在试验荷载试验下各测点相对残余应变均小于20%，说明处于正常的弹性工作状态，实测最大拉应力为3.6 MPa，锚固块的强度满足设计要求；在设计索力工况下，能够满足正常使用要求，且具有足够的安全储备。