层间隔震结构摩擦摆控制系统参数影响分析

段存坤，张春巍，2

（1.青岛理工大学 土木工程学院，山东青岛 266033；2.沈阳工业大学多学科基础设施工程研究中心，辽宁沈阳 110870）

引言

1985年Zayas等［1-2］对传统平面摩擦滑移系统进行改进提出了摩擦摆支座系统（friction pendulum system，FPS），隔震支座的变形通过其滑动面的滑动可以有效控制，具有自复位、稳定性良好、造价低廉等优点，受到了国内外学者的广泛关注。由铰接滑块与上支座板组成的机械关节使滑块沿下支座板滑道滑动时上支座板保持水平。滑道与滑块之间的接触面涂有低摩擦材料，如Teflon材料等，而且滑道半径相同。当结构受到的地震作用大于静摩擦力时，上部结构沿着滑道滑动面发生单摆状运动，支座水平力为上部结构由滑道上升而产生恢复力和滑道摩擦力的合力。通过摩擦系数来控制摩擦摆系统的阻尼，选择合适的滑道半径来控制摩擦摆系统的周期和刚度［3-6］。

除了基础隔震技术外，在一些建筑增层加固或特殊结构中，层间隔震技术因其特有的优势逐渐受到重视。通过将中间层改装成隔震层，将结构的层间变形集中在隔震层上，使高层建筑结构由2个高宽比较小的叠加结构组成，使高柔结构在地震作用下以剪切变形为主，克服了采用基础隔震技术时隔震层因水平变形过大导致支座剪压破坏从而发生结构倾覆倒塌的缺点。摩擦摆支座则可以安装在中间层或在基础顶部，能削弱传递到结构中的水平力和消耗振动能量［7-12］。

国内外很多学者通过试验研究和理论分析对摩擦摆支座的减震隔震性能进行了充分研究［12-19］，研究表明采用摩擦摆支座隔震后结构地震响应可以有效控制，而且隔震层相对位移可以通过改变摩擦摆接触面摩擦系数与滑道半径进行有效控制，因此对于控制上部结构地震响应与隔震层相对位移存在最优摩擦系数与滑道半径值，但是目前将摩擦摆支座与层间隔震技术结合起来的应用研究较少［16］。文中通过结合摩擦摆支座与层间隔震技术的优势，研究了基于摩擦摆支座的结构层间隔震控制问题，对摩擦摆层间隔震结构建立了有限元模型并进行了参数化分析，研究了上部结构地震响应与隔震层变形在摩擦系数与滑道半径变化下的规律，探讨了隔震层位置的影响。

1 基于摩擦摆支座的层间隔震结构减震机理

摩擦摆支座由球面滑道下支座板，铰接滑块以及连接上部结构的上支座板组成，如图1所示。摩擦摆支座的减震机理从2个方面分析：一方面是当地震动作用在圆弧面滑道上时，铰接滑块在滑道内滑动隔离一部分地震能量；另一方面是通过铰接滑块在圆弧面滑道滑动，接触面之间的相互摩擦消耗一部分能量。

首先，从受力的角度分析摩擦摆的减震机理，由于铰接滑块沿摩擦摆下支座板圆弧面滑道运动，摩擦摆支座可以作为单摆系统进行简化，其中滑道半径与滑块滑面半径均为R，下支座板圆弧面滑道竖向对称轴与滑块之间的转角为θ，以逆时针方向为正，如图2所示。水平位移为D=Rsinθ；上部结构的垂直载荷为W=mg，滑块的正压力为N=Wcosθ；摩擦力为其中μ为摩擦系数。摩擦摆水平力为F，在圆弧中心利用弯矩的静力平衡原理，可写成摩擦力和恢复力的组合，

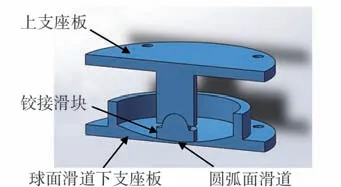
图1 摩擦摆支座Fig.1 Friction pendulum system

即

当θ很小时，可简化为：

摩擦摆支座滞回曲线如图3所示，kh为W/R，即摩擦摆支座的摆动刚度；ki=μW/dy即摩擦摆支座的初始刚度，dy为摩擦摆支座的屈服位移，即克服静摩擦力滑行的微小位移，等效刚度即

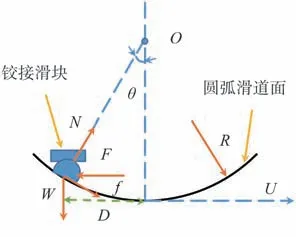
图2 摩擦摆计算模型Fig.2 Calculation model of FPS

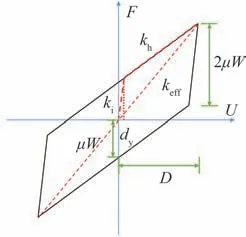
图3 摩擦摆滞回模型Fig.3 Hysteretic model of FPS

隔震效果可以通过具有集中质量的线性弹性系统来研究，这是上部结构的质量和刚度沿结构高度分布的模型的极端简化。图4显示了考虑中的结构系统，该结构系统是一个理想的N层剪切型建筑，带有摩擦摆支座。在每个楼层和基础质量处，考虑一个横向动态自由度。因此，对于N层结构，动力自由度为N+1。

图4 摩擦摆层间隔震结构示意图Fig.4 Model of N-stories FPS inter-story isolation structure

结合摩擦摆支座物理模型，分别对隔震层上部结构、下部结构和隔震层建立如下动力方程：

上部结构的运动方程：

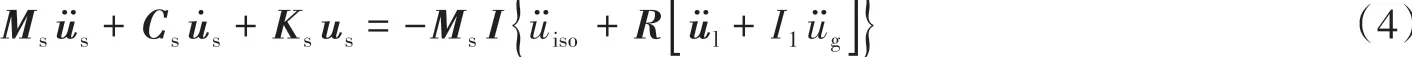
隔震层的运动方程：

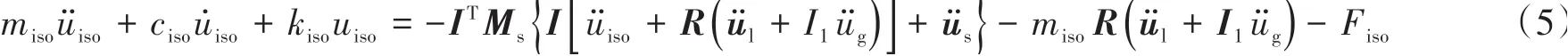
下部结构的运动方程：

式中：Ms、Ml分别为隔震层上部结构和隔震层下部结构的质量矩阵；Ks、Kl分别为隔震层上部结构和隔震层下部结构的刚度矩阵；miso为隔震层质量系数；kiso、ciso分别为隔震层附加的刚度系数与阻尼系数；us、u̇s、üs分别为上部结构同隔震层之间的相对位移、相对速度和相对加速度向量；ul、u̇l、ül分别表示下部结构同地面之间的相对位移、相对速度和相对加速度向量；uiso、u̇iso、üiso分别为隔震层同下部结构之间的相对位移、相对速度和相对加速度；üg为地面加速度；R为地震作用的影响系数矩阵，即R={ }0 0…1；I、I1分别为m阶和n阶单位列向量；Fiso为摩擦摆支座的水平力；Cs、Cl分别为上部结构和下部结构的阻尼矩阵。采用振型正交阻尼模型，即C=αM+βK。其中，

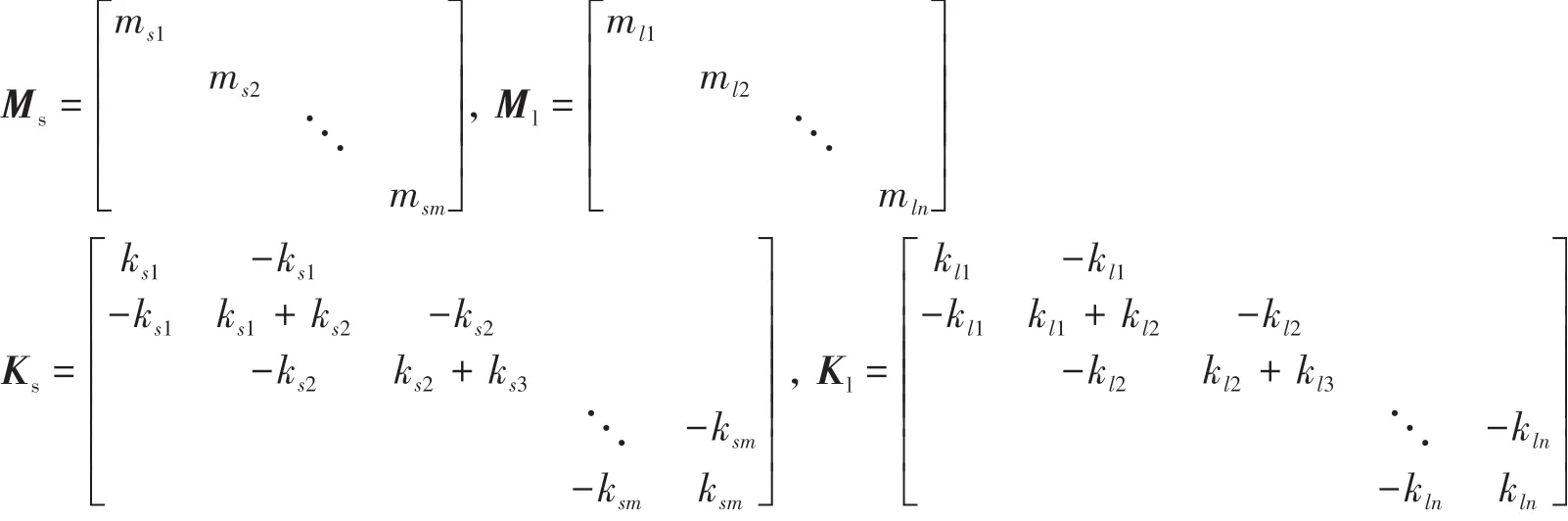
将以上列式合写得到结构的整体运动方程为：

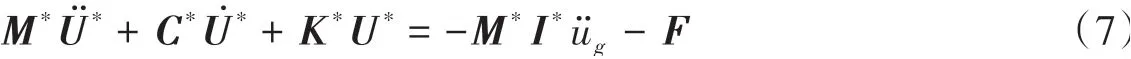
式中：M*、C*、K*、Ü*、U̇*、U*为广义质量、阻尼、刚度、加速度、速度与位移矩阵；F为广义荷载矩阵；I*为广义单位矩阵。其中，

另一方面，减震机理从耗能的角度分析，由图3可知，在水平力或地震作用下，铰接滑块在滑道内滑动摩擦所消耗的能量即滞回曲线所包裹的面积。

2 有限元建模与分析

图5 摩擦摆支座模型Fig.5 The model of friction pendulum system

采用ANSYS有限元软件对摩擦摆支座建立了有限元模型，该支座的设计位移为±40 mm，滑动面的平面半径为200 mm，如图5所示。整个摩擦摆隔震支座采用20节点六面体单元（Solid186），钢材的弹性模量为E=2×105MPa，泊松比υ=0.3，密度ρ=7.85×103kg/m3。在ANSYS有限元软件中摩擦系数定义为一常数，即接触面的切向摩擦力遵循库仑定律，动静摩擦系数相同，不能考虑速度与摩擦系数的相关性。通常，用于基底隔震时滑动面方向朝上；而用于层间隔震时滑动面方向朝下［15］。

有限元模型取自第3阶段地震作用9层Benchmark结构［20］，设计模型平面尺寸为0.5 m×0.5 m，高2.065 m，首层层高0.305 m，其余各层层高均为0.22 m，结构高宽比为4.13。以9层钢结构模型和摩擦摆支座为原型，由柱和板组成的9层钢框架结构。基于已有的振动台试验结果，选取第8层层间隔震结构为代表。采用Beam188单元模拟柱构件，采用Shell181单元模拟板构件，应用有限元软件建立了原结构与摩擦摆层间隔震结构的有限元模型。选取了4个具有重要水平分量的典型地震动，分别为1940年El Centro地震动，1952年Taft地震动，1979年Imperial Valley地震动，1994年Northridge地震动。PGA考虑0.1，0.15，0.2、0.25 g这4种情况。在本数值模拟分析之前采用Matlab编程语言，进行了不同地震动输入下的时程分析并从讨论了摩擦系数、滑道半径与隔震层位置的影响。在已有数值分析结果中，滑道半径的有效范围为150 mm至200 mm。数值分析的内容较多，因此不在这里展开阐述。摩擦摆支座的设计需要根据所隔震的结构进行，并进行相关的数值分析来确定其参数的选取范围，否则相关参数的选取不佳会起到相反的控制效果。

3 隔震效果分析

3.1 模态分析

原结构第1阶自振频率为2.252 7 Hz，第8层隔震时第1阶自振频率为1.597 3 Hz，采用摩擦摆层间隔震技术可以延长结构自振周期，如表1所示。同时，随着滑道半径的增大，摩擦摆层间隔震结构自振频率受到的影响较小。由图6可知，原结构与摩擦摆层间隔震结构的前两阶振型为沿纵跨方向和横跨方向的水平向平动，第3阶的振型绕竖向发生扭转。

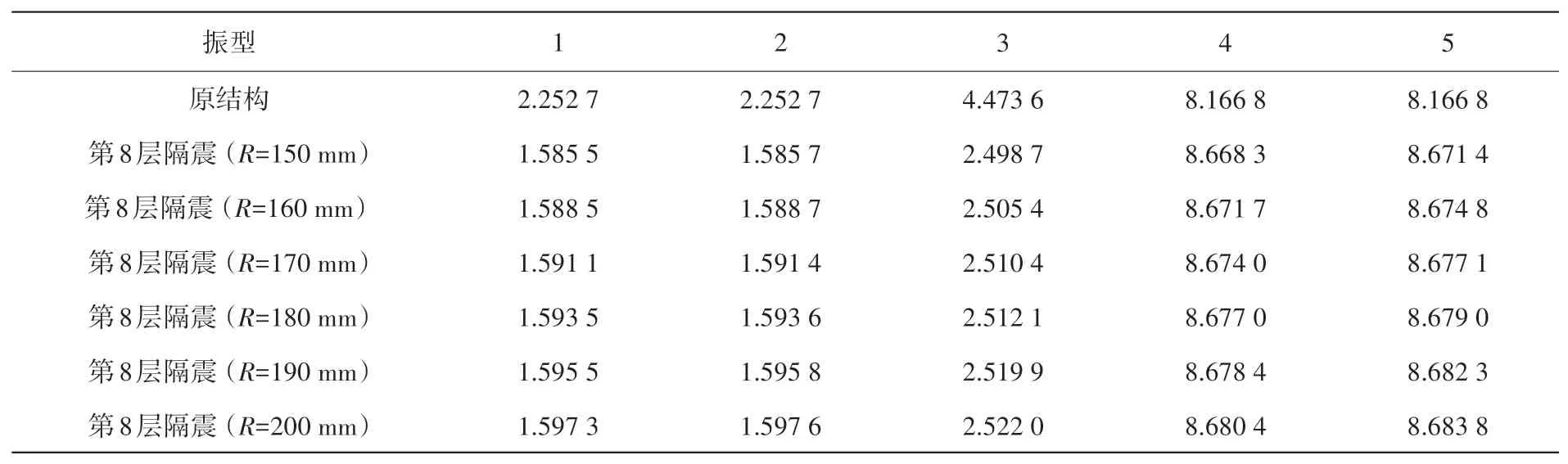
表1 结构自振频率Table 1 Natural frequency of structure Hz

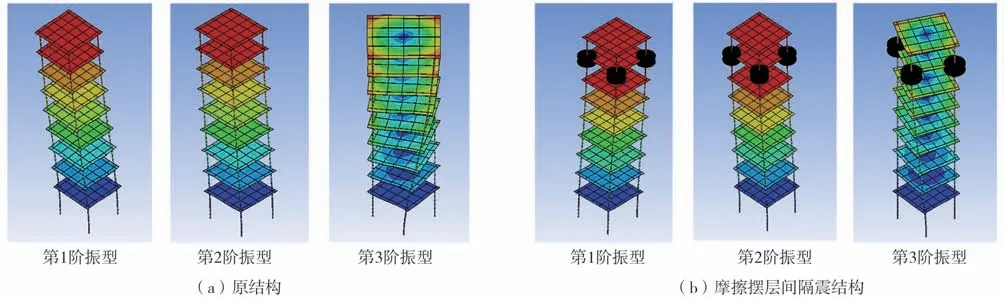
图6 前3阶振型Fig.6 The first three modes

3.2 动力时程分析

摩擦摆层间隔震结构的顶层加速度峰值明显小于原结构的顶层加速度峰值，摩擦摆层间隔震技术能够有效抑制结构响应，“削弱”了高频率的地震波，同时消耗地震作用输入能量，控制效果明显，如图7，表2所示。此外，摩擦摆层间隔震结构的顶层位移时程曲线接近于原结构顶层位移时程曲线，走势大致相同。

结构层间加速度有效值与层间位移曲线如图8所示。原结构与摩擦摆层间隔震结构的楼层加速度随着楼层的升高而增大，而摩擦摆层间隔震结构的楼层加速度明显小于原结构楼层加速度，且下部结构加速度响应也得到了抑制，摩擦摆层间隔震技术控制效果明显。此外，原结构与摩擦摆层间隔震结构的结构层间位移变化随着楼层的升高位移减小，摩擦摆层间隔震结构的层间位移则主要集中在摩擦摆支座上，下部结构的位移响应则明显小于原结构的。

表2 顶层加速度峰值与位移峰值（滑道半径=200 mm，PGA=0.25 g）Table 2 Top peak acceleration value and peak displacement value（Radius=200 mm，PGA=0.25 g）

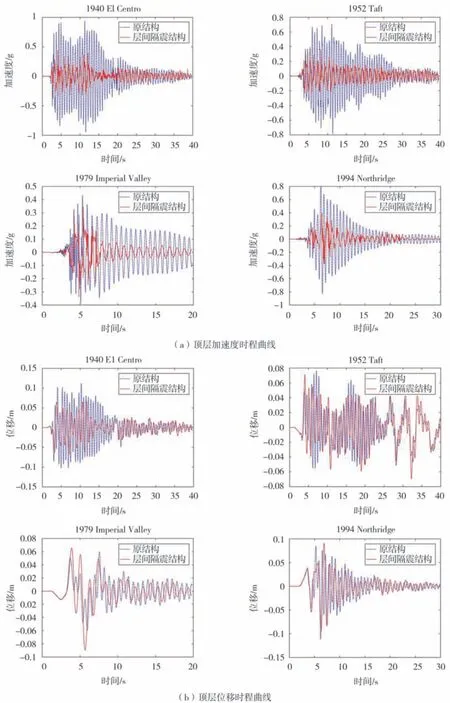
图7 顶层加速度和位移时程曲线Fig.7 Top acceleration and displacement time history curve

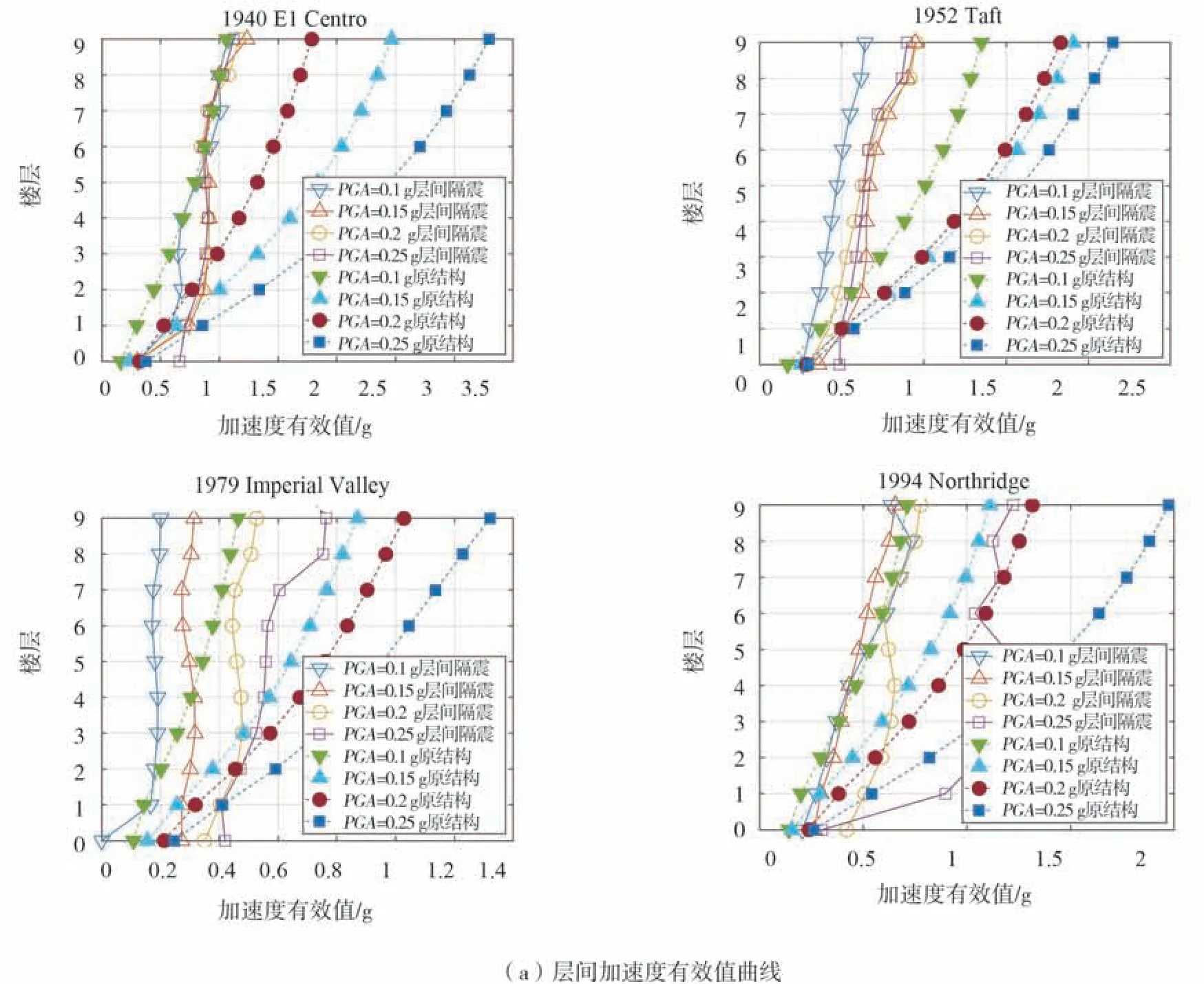
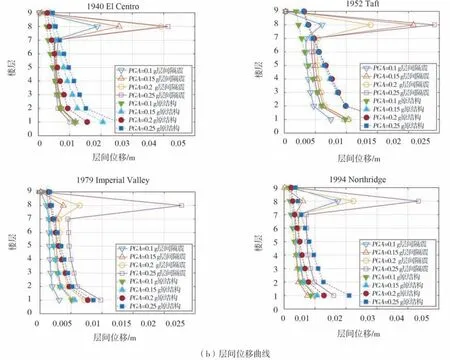
图8 层间加速度有效值曲线与层间位移曲线Fig.8 RMS value of inter-story acceleration curve and inter-story displacement curve

4 隔震控制参数分析

4.1 摩擦系数的影响

图9为摩擦摆摩擦系数对结构顶层加速度衰减率与摩擦摆相对位移的影响。加速度衰减率定义如式（8）所示，

以El Centro地震动与Taft地震动为例，顶层加速度衰减率随着摩擦系数的增大而增大；摩擦系数增大的同时增大了摩擦摆初始刚度，使摩擦摆耗能能力增强，从而有效减小了结构响应；此外PGA越大，控制效果越好，在0.25 g输入时控制效果在50%～70%之间。另一方面，摩擦摆支座相对位移随着摩擦系数的增大而减小，随着PGA的增大而增大，存在一个特定的摩擦系数值使上部结构的加速度响应和摩擦摆相对位移最小。当摩擦系数大于0.02时，摩擦摆相对位移减小缓慢，这主要是由于摩擦摆进入粘滞状态，而且随着摩擦系数的增大逐渐接近铰支座，这将不利于摩擦摆的自由摆动，影响其隔震性能，因此应该限制摩擦系数过大，防止粘滞现象的发生。通过设计最佳摩擦摆摩擦系数，在不增加结构顶层加速度的情况下，可以显著减小摩擦摆相对位移。

在遭遇Imperial Valley与Northridge这2种近断层地震时，随着摩擦系数的增大，顶层加速度衰减率增大且摩擦摆相对位移随着减小。在0.1～0.2 g输入时，摩擦摆相对位移较小且加速度衰减率较大；通过对比试验结果，此时的摩擦摆基本上没有滑动，相对位移较小，进入了粘滞状态，地震能量大部分靠结构自身消耗，由此说明摩擦摆层间隔震技术在遭遇近断层地震尤其是小震情况时不能充分发挥性能。在0.25 g输入时，摩擦摆层间隔震结构的隔震效果较差且摩擦摆相对位移较大；并且在振动台试验中输入Northridge 0.25 g地震动时，上下板之间发生碰撞，摩擦摆相对位移超过设计行程。这表明在遭遇近断层脉冲地震作用时，摩擦摆层间隔震结构存在因摩擦摆支座相对位移过大而发生碰撞破坏的可能性。由此表明，在采用摩擦摆层间隔震技术时也应考虑相应的限位技术，避免在遭遇强动力荷载时发生碰撞破坏。

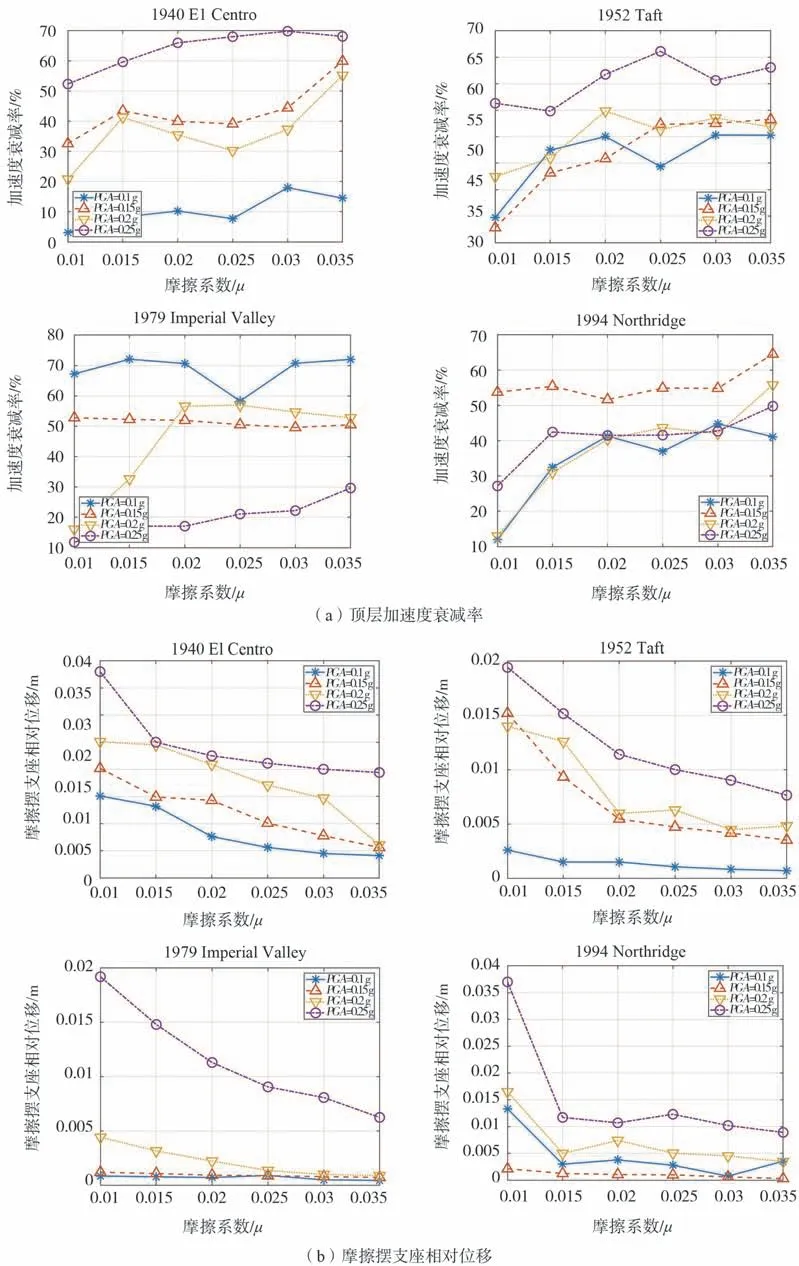
图9 摩擦摆支座摩擦系数的影响Fig.9 Influence of FPS friction coefficient

4.2 滑道半径的影响

图10为摩擦摆滑道半径对结构顶层加速度衰减率与摩擦摆相对位移的影响。在遭遇不同地震动时，结构响应受摩擦摆滑道半径的影响略有不同。首先以El Centro地震动与Taft地震动为例，结构顶层加速度衰减率随着滑道半径的增大而增大；滑道半径的增加降低了支座的摆动刚度，但不影响摩擦摆耗能能力，减小了结构响应，因此滑道半径越大效果越优；特别地，在0.25 g输入时，控制效果在20%～60%之间变化，说明大震情况下摩擦摆层间隔震技术隔震效果显著，可充分发挥性能。在输入El Centro 0.2 g地震动与El Centro 0.25 g地震动，摩擦摆相对位移随着滑道半径的增大是先增大后减小再增大的趋势，而在0.1 g与0.15 g时，随着滑道半径的增大，摩擦摆相对位移也随着增大；输入Taft地震动时，摩擦摆相对位移随着滑道半径的增大而增大，且随PGA呈层次状变化，在0.1 g输入时滑动位移最小，摩擦摆基本上没有滑动。在遭遇大震情况时，摩擦摆采取200 mm的滑道半径可以获得良好的隔震效果且将结构变形集中在摩擦摆上。

在遭遇Imperial Valley近断层地震动时，结构顶层加速度衰减率随着滑道半径的增大而增大，在0.1 g与0.15 g时，控制效果在20%～65%之间变化，而在0.2 g与0.25 g时，则控制效果在20%以下；摩擦摆相对位移则随着滑道半径的增大而增大，仅在0.25 g时存在较大相对位移，而在0.1～0.2 g时，摩擦摆相对位移较小。由此可知摩擦摆采取190～200 mm滑道半径可以获得相对较好的控制效果且控制结构变形。在遭遇Northridge近断层地震动时，摩擦摆的滑道半径采取170～180 mm时，加速度衰减率在40%～80%之间变化，获得了良好的控制效果，同时在大震情况时的隔震效果是优于小震情况下的；摩擦摆相对位移则随着滑道半径的增大而增大，仅在0.25 g时存在较大相对位移。合理选择摩擦摆滑道半径，在不增加摩擦摆相对位移的情况下，可以显著减小结构顶层加速度。

图10 摩擦摆支座滑道半径的影响Fig.10 Influence of FPS slideway radius

4.3 隔震层位置的影响

图11为隔震前后X向各阶振型频率的比值。该图表明，随着隔震层的上升，隔震后与隔震前的1阶振型频率比减小，结构周期得到了延长。2阶振型与3阶振型频率变化明显大于1阶，这表明2阶与3阶频率所受影响比1阶大，频率变化快。此外，可以注意到，2阶与3阶振型频率变化当摩擦摆支座安装于4层时存在明显的拐点。

模态参与质量系数只与振型有关，利用不同振型的正交性，所有模态参与质量系数之和为1，这表明模态参与质量系数相当于一权重分配系数，模态参与质量系数直接表明相应振型的影响在所有振型中所占的比重。如表3与图12所示为隔震前后模态参与质量系数。隔震后1阶与2阶模态参与质量系数之和在95%以上，这意味隔震能迅速提高1阶振型和2阶振型的效应的权重，而2阶以上振型的贡献则随之迅速降低。当摩擦摆支座安装于4层与5层时，2阶振型的模态参与质量系数分别为42%与12%，上层结构响应中以剪切和弯曲变形为主。摩擦摆层间隔震结构在地震作用下响应不仅仅包括以剪切变形为主的第1阶振型，也包含上部结构的弯曲变形，忽略上部结构剪切和弯曲变形的振型将带来比较大的计算误差。

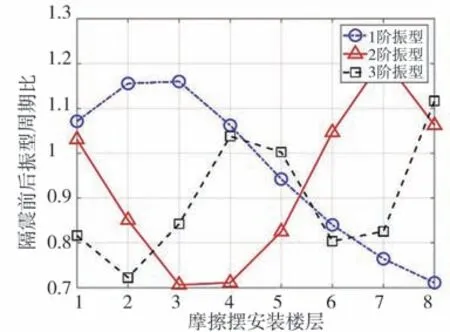
图11 隔震前后振型周期比Fig.11 Mode period ratio before and after inter-story isolation

表3 X向模态参与质量系数Table 3 X-direction mode participation mass coefficients %

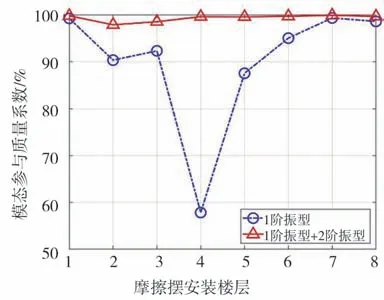
图12 模态参与质量系数Fig.12 Mode participation mass coefficient

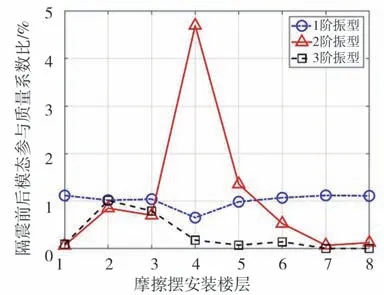
图13 隔震前后模态参与质量系数之比Fig.13 Mode participation mass coefficient ratio of before and after inter-story isolation

图13为隔震前后模态参与质量系数之比，1阶模态参与质量系数之比基本稳定在1.0。随着隔震层的上升，2阶的模态参与质量系数比先增大后下降，当摩擦摆支座安装于4层与5层时明显大于1；3阶及以上振型的作用随隔震层的上升迅速降低，可以认为设置隔震后3阶及以上振型已基本没有影响。为实现较好的减震效果，隔震设计应以采用适宜的隔震层位置为主，使高阶振型影响的减少幅度超过1阶振型的增大幅度。高阶振型的地震影响系数通常大于低阶振型，减少高阶振型的权重也就间接降低了地震的基底剪力，这是摩擦摆层间隔震结构减震机理的特殊之处。

5 振动台试验

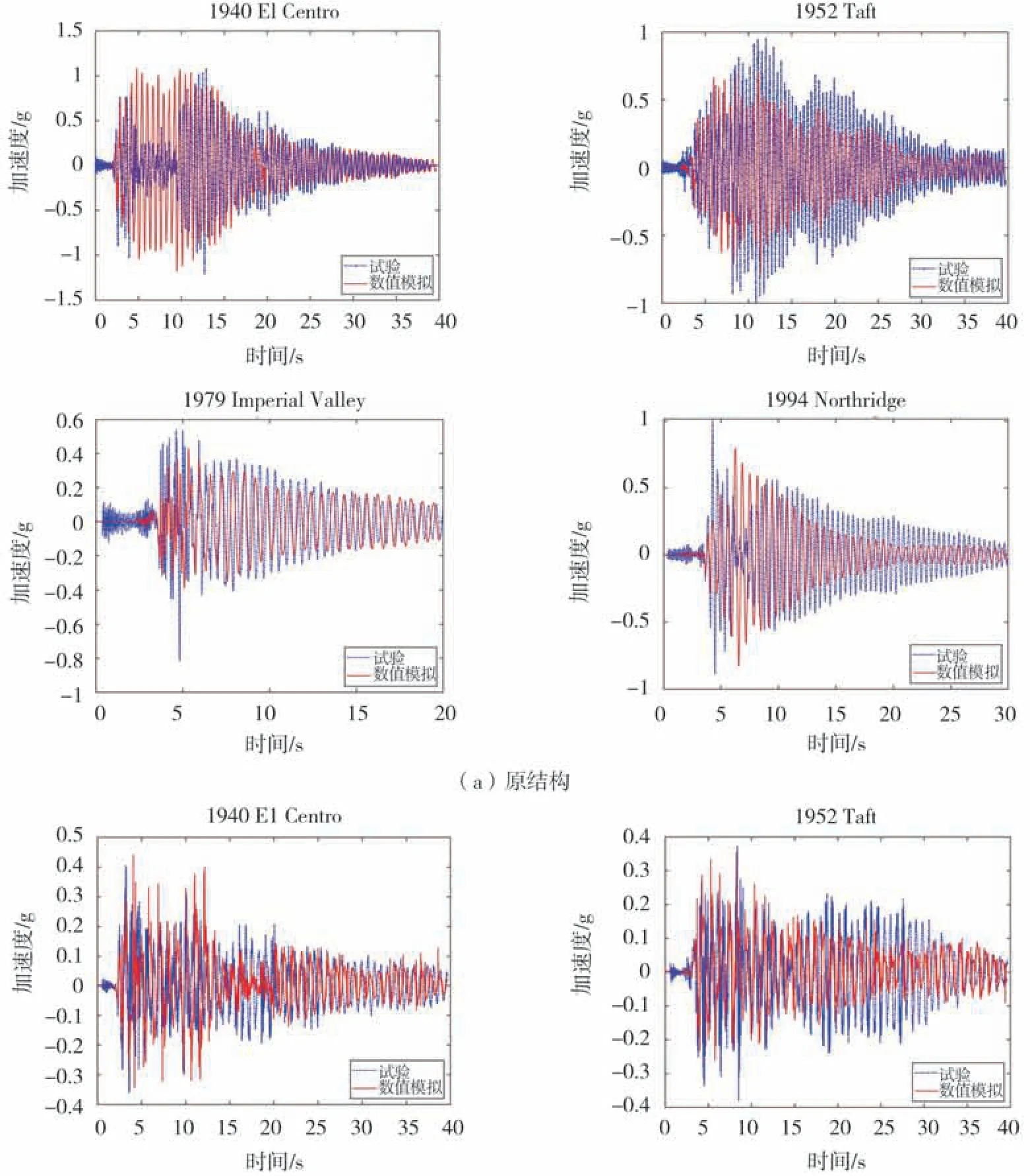
为了验证有限元模型的有效性，对相应的9层钢框架试验模型进行了振动台试验，如图14所示。试验采用Quanser公司Shake table 3型71.1 cm×71.1 cm双向输入振动台，载荷100 kg时最大地震激励大小为1 g，XY向行程分别为10.8 cm。在各楼层与振动台的台面中间布置加速度传感器，共采用10个Lord Sensing Wireless Sensor。振动台试验中台面输入的地震动与数值模拟分析中的地震动相同，且峰值大小相同。

图15列出了原结构与摩擦摆层间隔震结构的顶层加速度时程与层间加速度有效值的有限元分析结果与试验结果的对比曲线。从图中可以看出，有限元模型能够很好地模拟摩擦摆层间隔震结构与原结构的地震反应，并证明有限元分析结果和试验结果吻合良好，趋势相同。

图14 试验模型Fig.14 Photograph of tested model

6 结论

文中以摩擦系数、滑道半径及隔震层位置为变量，研究了基于摩擦摆支座的结构层间隔震控制系统在4种地震动下的地震响应控制规律，得出以下结论：

（1）层间隔震控制能够有效抑制结构响应，有效削弱地震作用致结构的高频振动响应，消耗地震作用输入能量。随着摩擦系数的增大，顶层加速度衰减率随着增大，而摩擦摆相对位移随着减小；摩擦系数增大的同时增大了摩擦摆初始刚度，摩擦摆耗能能力增强，从而有效减小了结构响应。通过设计最佳摩擦摆摩擦系数，在不增加结构顶层加速度的情况下，可以显著减小摩擦摆相对位移。

（2）随着滑道半径的增大，顶层加速度衰减率随着增大，摩擦摆相对位移也随着增大；滑道半径的增加使支座的摆动刚度降低，但不影响摩擦摆耗能能力，因此减小了结构响应。合理选择摩擦摆滑道半径，在不增加摩擦摆相对位移的情况下，可以显著减小结构顶层加速度。

（3）摩擦摆层间隔震结构调整了体系各振型的贡献比例，降低了高阶振型的影响，同时隔震后结构周期延长，高阶振型周期的延长进一步降低了高阶振型的贡献，实现减震的目的。为取得较好的减震效果，建议摩擦摆支座安装位置为层间隔震结构的顶部楼层。