聚氨酯限位弹簧超弹本构模型的建立及静力学分析*
2022-11-15贾维辉栗源涛朱金梅鉴冉冉朱维浩曾宪奎
贾维辉,郭 鹏,栗源涛,朱金梅,鉴冉冉,朱维浩,曾宪奎
(青岛科技大学 机电工程学院,山东 青岛 266061)
近几年,轨道交通行业的快速发展,不断对列车运行安全性和乘坐舒适性提出越来越高要求,因此振动和噪声成为高速列车的急需解决的重要难题。限位弹簧作为减振阻尼系统的元件之一,能有效减少车厢内的振动,降低车内噪音,从而提高乘坐舒适度、车辆运行安全性。因此研制满足高速磁悬浮列车技术要求的限位弹簧,满足最大效益的减振要求是非常必要的。
聚氨酯是由异氰酸酯和多元醇经过缩聚反应生成的一种新型材料,与传统塑料相比有更好的耐磨性和弹性记忆,较橡胶具有更强的承载性和耐撕裂性,传统金属材料与其在降噪、耐损耗、生产加工成本方面具有显著优势[1-2]。利用聚氨酯材料制得的减振器存在一定的动静刚度比,使其具有优异的抗冲击性能和可变形性能[3],因此成为高速列车限位弹簧减振材料的首选。葛孚宁等[4]用有限软件对聚氨酯减振器进行了模拟仿真,实验证明了与传统减振器对比聚氨酯减振器具有更加优异的承载范围、承载能力、承载效果。李洪潘等[5]系统归纳了聚氨酯材料的性能参数,由此构建了最符合的聚氨酯的本构模型,在本构模型的基础上对减振器进行了数值模拟,实现对聚氨酯减振器结构参数的优化设计。上官文斌等[6]对橡胶材料做了了拉伸实验,通过有限元分析,采用模拟效果最佳的Ogden本构模型来模拟分析减振器的三向静刚度,得出在大变形甚至更特殊的工作状态下,目前采用有限元来分析黏弹性阻尼减振器的实验数据不足,如果希望获得有效模拟结果需要大量实验数据。赵传奇等[7]通过有限元分析软件对聚氨酯减振器进行了模拟仿真,验证了其承载能力、承载范围、承载效果。
为此,本文结合实际研究情况与文献学习经验,针对磁悬浮列车限位弹簧应用在复杂力学环境、高度重要场合的客观事实,立足聚氨酯弹性体本身的结构性能参数,综合讨论与分析,最终确定了牌号为美瑞E190的聚酯型热塑性聚氨酯,对其进行拉伸实验,确定了拟合效果最好的超弹本构模型。本文利用ABAQUS软件建立了轴对称模型并对聚氨酯限位弹簧进行了静力学仿真分析,进而确定了材料参数。
1 限位弹簧的材料选择
参考《高速磁浮列车悬浮架用限位弹簧技术条件》对限位弹簧的减振要求,本文设计的聚氨酯减振器主要在列车车厢底部承受竖直方向的载荷。根据图1显示的位移-载荷曲线要求对弹簧进行静态拉伸实验。
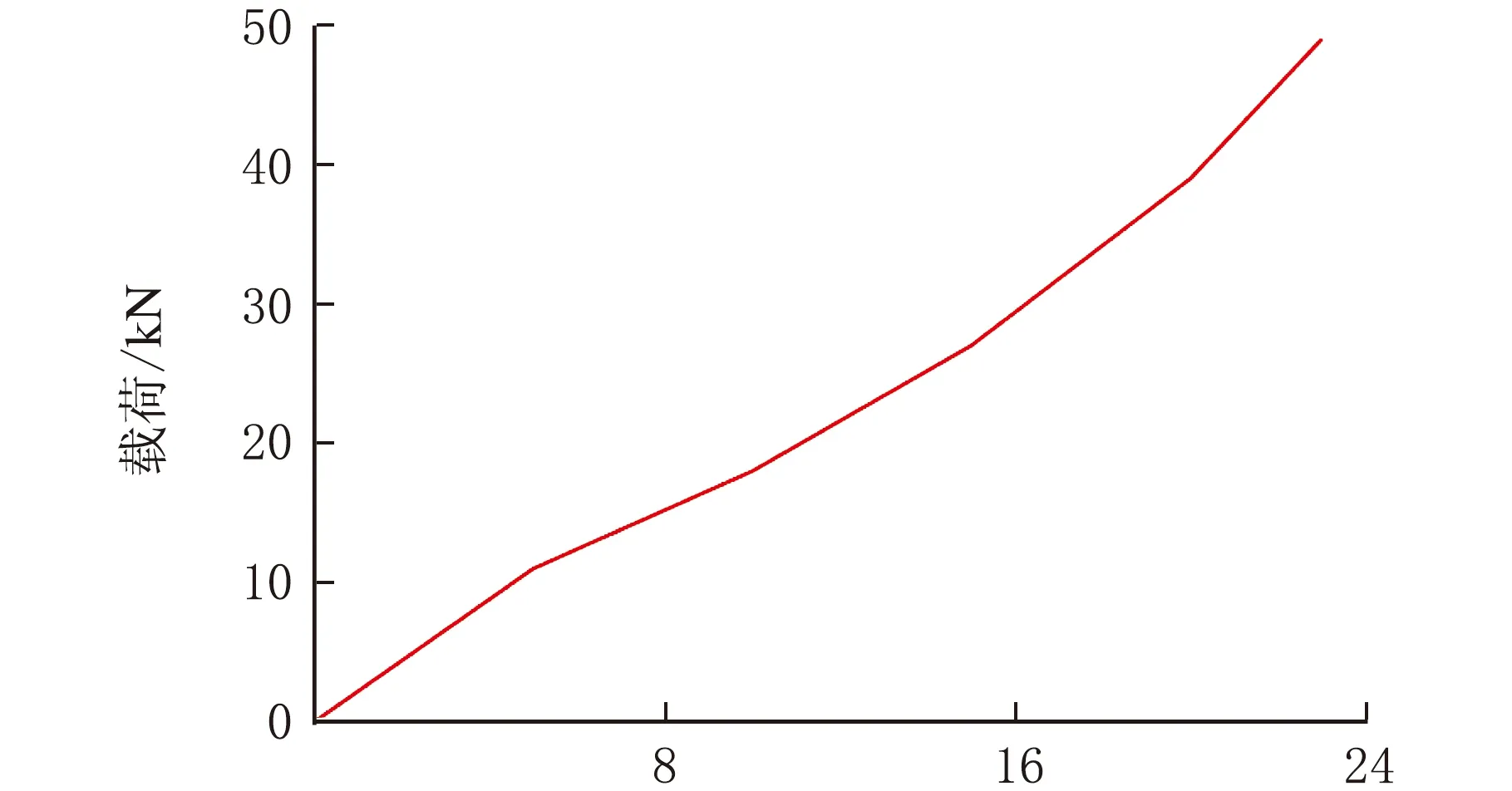
位移/mm
通过技术条件中位移-载荷曲线可以计算出限位弹簧拉伸强度在36.418 MPa左右。通常情况下,当提高材料的硬度时,拉伸强度也会与之提升,然而材料的伸长率和韧性等性能会有不同程度的降低[8]。由公式(1)可得到材料硬度(HS)与杨氏模量(E)拟合实验数据的关系式为[9]:
E=(15.75+2.15HS)/1001HS
(1)
因此通过计算可以得出,限位弹簧减振材料的邵尔A硬度在94左右,结果见表1。

表1 不同聚氨酯产品材料性能
表1展示了巴斯夫、路博润、亨斯迈和美瑞等国内外著名聚氨酯产品的不同型号在密度、邵尔A硬度、拉伸强度三个性能参数的差异,通过数值的直观判断,牌号为美瑞E190的聚酯型热塑性聚氨酯邵尔A硬度为92、拉伸强度为36 MPa,其刚度系数可以满足限位弹簧在不同温度条件下的需求。除此之外,美瑞E190的聚酯型热塑性聚氨酯还具有优异的耐磨性、耐溶剂性以及抗压缩变形性。
2 聚氨酯基础实验和超弹本构模型拟合
2.1 聚氨酯弹性体基础实验
为了研究聚氨酯弹性体的力学性能实验,对美瑞E190热塑性聚氨酯弹性体分别进行单轴拉伸实验、多轴拉伸实验以及平面拉伸实验。
2.1.1 单轴拉伸实验
本实验采用的是EUT10KV2高弹性体拉伸试验机,实验过程参照GB/T 528—2009[10]。把试样裁成I型的哑铃状,试样宽度为12.0 mm,长度为25.0 mm。由于在拉伸测试实验中不同的实验选定的拉伸速率是不同的,因此本实验依据实际实验条件确定了拉伸速率,项英[11]选用的拉伸速率为30 mm/min,而本试验机选择拉伸速率为40 mm/min。把拉伸长度控制在标距长度的80%以内,在经历往复循环三次加载卸载后,可以得到测试实验数据。
2.1.2 多轴拉伸实验
本实验所采用的设备是EBTH250KV2高弹性体多轴拉伸试验机,选取的试样形状为圆盘状,以此可以实现径向方向上的等轴拉伸。将夹具放置在试样的中间部位以此在实验过程中通过夹具产生的拉力使试样达到彻底的双向应力应变状态,这种实验方法获得的双轴拉伸应变状态精确程度更高,因此可以取代双轴拉伸实验。加载速度为40 mm/min,采用单独的力传感器来测量各轴向力,与单轴拉伸实验加载方式相同。
2.1.3 平面拉伸实验
本实验所采用的是EUT10KV2高弹性拉伸试验机和ELE-1810M非接触式变形测量系统。本实验将试样剪裁成实验方向上长宽比为1∶11的矩形裁片,以此来获得纯平面拉伸应变状态。试验机的加载速率为40 mm/min,拉伸长度为标距长度的80%,与单轴拉伸实验加载方式相同。
2.2 实验数据的拟合
聚氨酯弹性体在三种不同拉伸实验的应力-应变曲线如图2~图4所示。三种实验的应力-应变曲线均呈现出高度非线性,在三种拉伸实验中应力-应变曲线中也不相似。
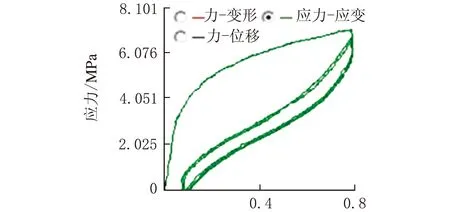
应变
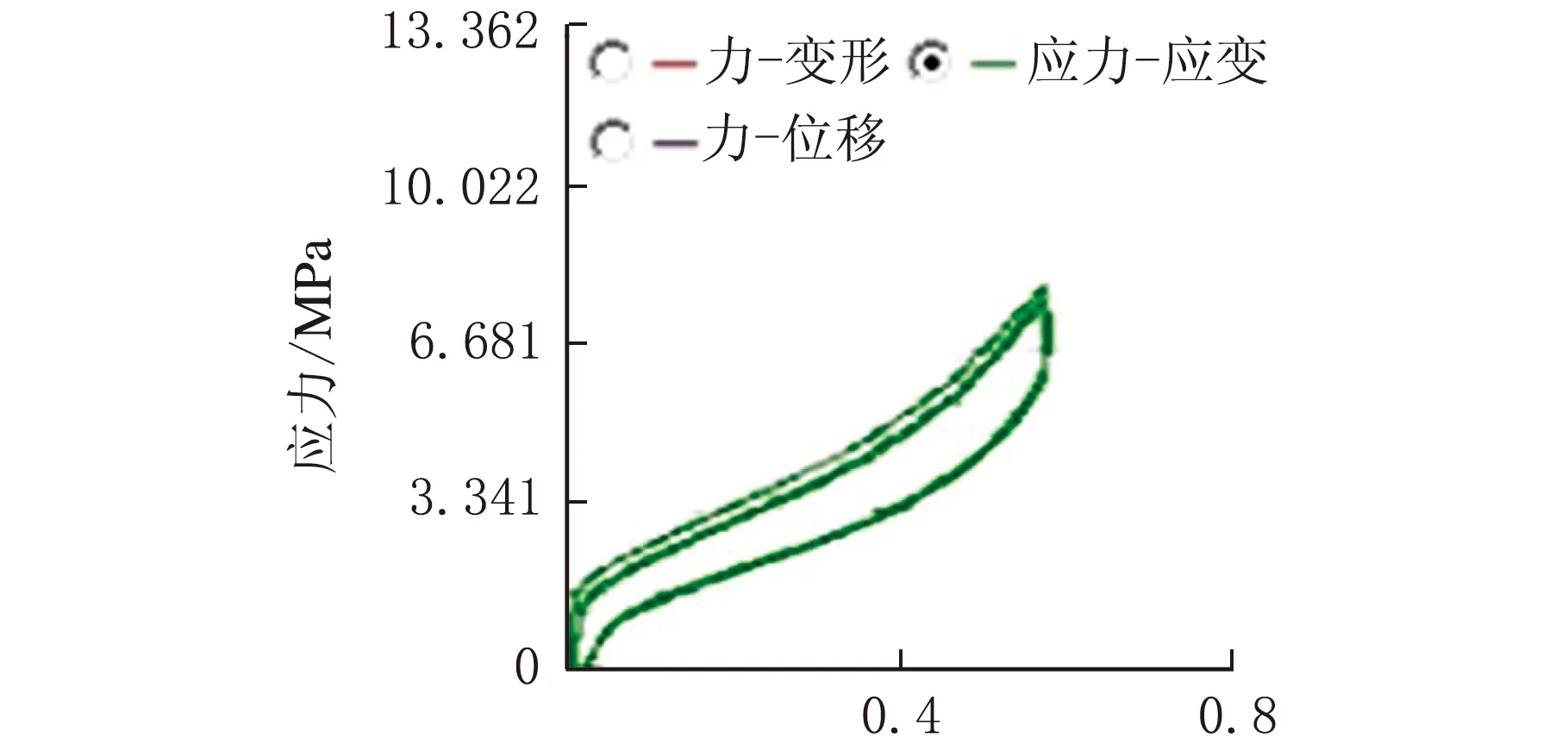
应变
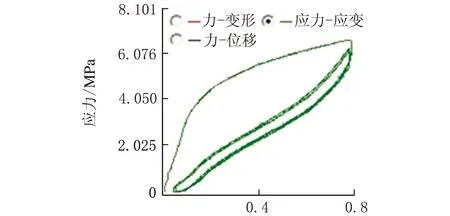
应变
通过对三种实验的应力-应变曲线图分析可以得到一个结论:即应力-应变曲线并不会因为相同的应变水平而出现重合的情况,在高分子材料多次加卸载过程中,所出现的这种现象被称为静态应力软化特性,也被称为Mullins效应[12-13]。要充分考虑Mullins效应对于表征某一材料各项性能的影响,因此为了消除Mullins效应的影响,则使材料的应力-应变曲线试样循环加载的条件下逐渐趋于稳定,此时方可开展相关的力学实验。如图5所示,本文选择最后一次应力-应变数据作为本构模型拟合参数数据。

拉伸应变/%
高分子材料的本构模型是指材料在受到拉伸、压缩作用过程表现出来的应力与应变的关系,高分子材料自身具有非线性特性,故不能像金属材料一样通过杨氏模量、泊松比就可对材料属性进行定义。目前,对于聚氨酯超弹性的理论模型研究也有较大的进展和完善[14-15]。本文选择常见的超弹本构模型Arruda-Boyce模型、Mooney-Rivlin模型、Reduced polynomial模型以及Ogden模型等进行参数拟合结果分析[16]。
单轴拉伸与参数拟合的应力-应变曲线见图6。

图6 单轴拉伸与参数拟合的应力-应变曲线
如图6所示,当应变水平在0.5以内时,各种模型所拟合曲线走势大致一样,Yeoh模型拟合出的效果是最好的;其次是Marlow模型;再次是Neo-Hookean、Ogden模型、Arruda-Boyce模型等低阶模型,在较少参数的条件下这几种模型即可达到拟合模型所要求的精度;高阶缩减多项式模型和Mooney-Rivlin模型拟合效果是比较差。当应变水平在0.5以上时,各种模型拟合的曲线有了不同的走势,Ogden N5~N6模型与实验曲线走势大致相同;Arruda-Boyce模型和Reduced polynomial N6模型的拟合效果一般;Ogden N4模型的最后偏离程度较大;Reduced polynomial N4~N5模型和Van der Waals模型拟合效果是最不好的,因为其模拟曲线与实验曲线不仅形状相差较大而且偏离程度很大,完全丧失精确性。
如图7所示,几种拟合出来的曲线与多轴拉伸实验数据曲线十分接近,在多重放大之后,得到Yeoh模型与Ogden高阶模型十分接近,这可能是因为该聚氨酯材料硬度较高,在多轴拉伸应力状态下可以得到接近实验数据的拟合结果。

图7 多轴拉伸与参数拟合的应力-应变曲线
如图8所示,在应变水平在0.5以下时,各种模型拟合出的曲线大致相同,其中Ogden N4~N5模型与Yeoh模型实验曲线是比较接近的;高阶缩减多项式拟合曲线与实验曲线也高度相近,但其拟合效果要比上述模型略低;Van der Waals模型、Mooney-Rivlin模型以及完全多项式模型N2由于在数据方面存在些许偏差,尽管其与拟合曲线形状趋势相同,也不能认定其拟合效果较好;Neo-Hookean模型等参数较少的本构模型拟合效果一般。应变水平在0.5以上时,Ogden N5模型和高阶缩减多项式模型拟合效果是比较好的;Ogden N6模型与实验曲线形状趋势相同;Mooney-Rivlin模型与实验曲线较为接近;Ogden N1~N2和Yeoh模型和Yeoh模型的拟合效果最不好。
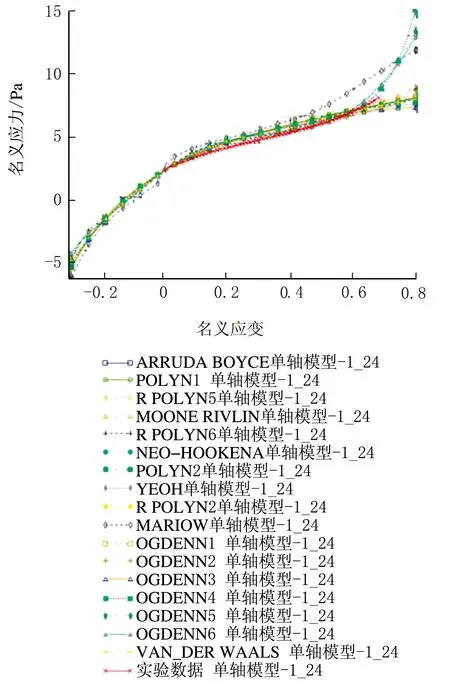
图8 平面拉伸与参数拟合的应力-应变曲线
以材料的实际拉伸实验数据为参照,将拟合本构模型数据来作对比,发现二者虽然有相近的趋势但仍客观存在着差异。研究人员通常会忽略通过拉伸实验数据拟合所得的材料应力-应变曲线存在的误差,所以所做的仿真模拟与实际工程材料数据总是存在不可消除的误差。
2.3 超弹本构模型的确定
实验拟合结果表明不同的模型得到的拟合结果高度相似,因此在评价拟合效果时仅仅通过拟合曲线显然不够客观,也不具备说服力,所以需要引入一个新的分析去判断拟合模型的数据点与实验测试的数据值的相近程度,以此来确定合适的超弹本构模型。
采用均方根误差可以实现对模拟数值与真实数值的偏离程度进行表征,以观察拟合误差的大小关系。均方根误差(RMSE)的计算公式如式(2)所示。
(2)
式中:Xobs,t为模型观测数值;Xmod el,t为模型实际数值。
拟合误差的计算公式见式(3)。
(3)
式中:E为拟合误差;Tfit,i为拟合数值;Ttest,i为测试数值。
通过计算可以得到不同拉伸实验下各模型的拟合误差,如表2所示。

表2 拉伸实验下的拟合误差
由表2可以得出:在单轴拉伸状态下,OgdenN5模型、完全多项式N2模型和A-B模型拟合效果最好,拟合误差较小;在多轴拉伸状态下,各模型之间的误差很小,Reduced polynomial N4模型和Ogden N4模型的拟合效果最好;在平面拉伸状态下,Reduced polynomial高阶模型、Yeoh模型和Ogden N5模型的拟合效果最好。考虑到限位弹簧的实际应变量,其制造材料的力学状态并不适用低阶本构模型来表征,结合实际应用场景和受力条件,采用Ogden N5模型对聚氨酯限位弹簧进行静力学分析。
3 限位弹簧的静力学分析
3.1 有限元模型的建立
限位弹簧的结构和承受载荷均具有轴对称性,在ABAQUS软件中建立轴对称模型进行模拟,逐步创建Part1限位弹簧轴对称模型和Part2压板模型两种模型,于Part2上创建参考点RP。
3.2 施加约束及边界条件设置
选用静态通用分析步,在增量步的设置中,初始增量步长设置为0.01,将下端钢板节点的所有的自由度进行约束,选择Part1-Part2为接触表面;约束2类型选择自接触,约束3选取右面表面Part1-1.Surf-4,在Step-1中分别设置约束4、约束5。选择实体单元CAX4RH,选取四面体网格划分,并对Part2进行强制位移,对限位弹簧底边的六个方向的自由度为零,使其完全固定。选择Part2的参考点RP,使其向下移动,U2设置为-23,对其进行强制位移。
3.3 模拟结果分析及优化
限位弹簧在压缩作用下会在横向方向膨胀而且横向空间较小,所以仅变换限位弹簧的高度来实现限位弹簧结构的最优设计。建立模型高度分别为70、75、80、85 mm的限位弹簧,进行静力学分析,从而得出限位弹簧在加载的过程中位移与载荷两者之间的变化关系(见图9)。

位移/mm
如图9所示,得到了不同高度时美瑞E190聚氨酯限位弹簧的位移-载荷曲线。通过对比图1中位移-载荷曲线可以得出,高度为80 mm、外径为80 mm、内径为21 mm的限位弹簧结构参数是满足高速列车限位弹簧承载变形条件。
限位弹簧在承受极限载荷以下的作用力时,变形范围必须要小于23 mm,图10为在位移载荷23 mm的作用下聚氨酯限位弹簧位移云图及最大主应力云图。
如图10所示,最优结构的聚氨酯限位弹簧的变形比较规则,在聚氨酯限位弹簧逐渐压缩的过程中,其最大主应力为1.161 MPa,远远小于材料拉伸断裂极限40 MPa,可得到设计的限位弹簧安全系数较高;选择美瑞E190作为减振材料,限位弹簧有了较为可靠的减振阻尼性能。

(a)位移云图
本文通过静力学分析验证了设计的聚氨酯限位弹簧具有功能可信性和使用价值。
4 结 论
(1)美瑞E190牌号的热塑性聚氨酯邵尔A硬度为92、拉伸强度为36 MPa,符合限位弹簧的多项技术条件及性能要求。
(2)在单轴拉伸状态下,Ogden N5模型、完全多项式N2模型和A-B模型拟合效果最好,拟合误差较小;在多轴拉伸状态下,各模型之间的误差很小,Reduced polynomial N4模型和Ogden N4模型的拟合效果最好;在平面拉伸状态下,Ogden N5模型、Yeoh模型和Reduced polynomial高阶模型的拟合效果最好。最终采取Ogden N5模型对聚氨酯限位弹簧进行静力学分析。
(3)设计的聚氨酯限位弹簧安全系数较高,并且以Mirathane-E190聚氨酯弹性体作为减振材料为限位弹簧提供了优良的减振阻尼性能。通过静力学分析验证了聚氨酯限位弹簧具有结构可靠性与功能可信性。
