硅橡胶减振器的非线性随机振动分析
2022-11-15段成红李芳妍罗翔鹏王福军刘镇溪
段成红,李芳妍,罗翔鹏,王 波,王福军,刘镇溪
(北京化工大学 机电工程学院,北京 100029)
电子设备在工作中,容易受到正弦振动、随机振动、冲击等环境的作用,会导致电子设备结构变形或损坏[1]。由于其具有超弹性,橡胶已经成为最重要的减振材料之一[2]。橡胶减振器是整个电子设备系统中固有频率最低的部位,对电子设备在随机振动、冲击等载荷下的响应具有决定性作用[3]。硅橡胶减振器具有宽温域适用性、高弹性、高阻尼和长寿命等优点[4],在某些复杂、苛刻的工作环境中,硅橡胶阻尼材料可以得到很好的应用[5],因此广泛应用于运输、电子产品、航空、航天、船舶、建筑等领域。硅橡胶减振器工作时,硅橡胶通过产生动态的应力应变,将一部分能量储存为势能[6];硅橡胶的阻尼特性将另一部分能量转换为热能耗散在空气中,从而达到减振的效果。
硅橡胶是一种超弹性材料[7],当采用简单的弹性模量来描述橡胶的本构关系时,与实验结果相差较大。因此,橡胶本构模型及参数的选取决定了有限元仿真的准确性和可靠性[8]。常用的超弹性本构模型有Mooney-Rivlin模型、Yeoh模型、Ogden以及Neo-Hookean模型[9-10]。屠璐琼等[11]采用Mooney-Rivlin模型描述橡胶的超弹性,并通过模拟单轴压缩实验过程验证了材料参数的准确性。张琦等[12]建立了硅橡胶的单轴压缩试验有限元模型,通过模拟仿真得出Yeoh模型可以在大应变时较好地描述橡胶材料的特性,Mooney-Rivlin模型在小应变和中等应变时可以较好地描述橡胶的特性。
对于不同种类、不同硬度的橡胶,其应力应变关系相差较大,需要基于材料的力学实验来研究橡胶减振器的非线性建模方法。橡胶材料的力学实验包括单轴、等轴、剪切以及体积实验。考虑到实验条件,进行等轴实验、剪切实验以及体积实验价格昂贵且耗时。潘宇倩等[13]验证了采用单轴拉伸实验拟合橡胶超弹性本构关系的可行性。肖全山等[14]根据单轴压缩与等轴拉伸的等价关系,拟合出Mooney-Rivlin模型的参数,可以较好描述减振器静变形的力学性能。目前主要通过单轴实验拟合Mooney-Rivlin橡胶超弹性本构模型,采用静态刚度仿真与实验验证的方法验证超弹性本构模型的准确性,因此,建立适用于非线性随机振动分析的硅橡胶减振器超弹性本构模型是十分必要的。
本文研究对象为带硅橡胶减振器的电子设备。首先对硅橡胶进行单轴压缩实验,拟合实验数据得到Mooney-Rivlin超弹性本构模型的材料参数C10和C01;然后使用MSC Patran/Nastran有限元分析软件进行非线性有限元建模和频率响应分析,通过有限元分析结果与振动实验结果对比,验证硅橡胶减振器非线性有限元模型的准确性;最后通过随机振动分析,验证硅橡胶减振器的减振效果。
1 有限元模型建立
1.1 几何模型
本文采用的硅橡胶减振器由两个T型减振垫、限位垫片和限位衬套组成,限位垫片和限位衬套用于固定T型减振垫,硅橡胶减振器的结构如图1所示。
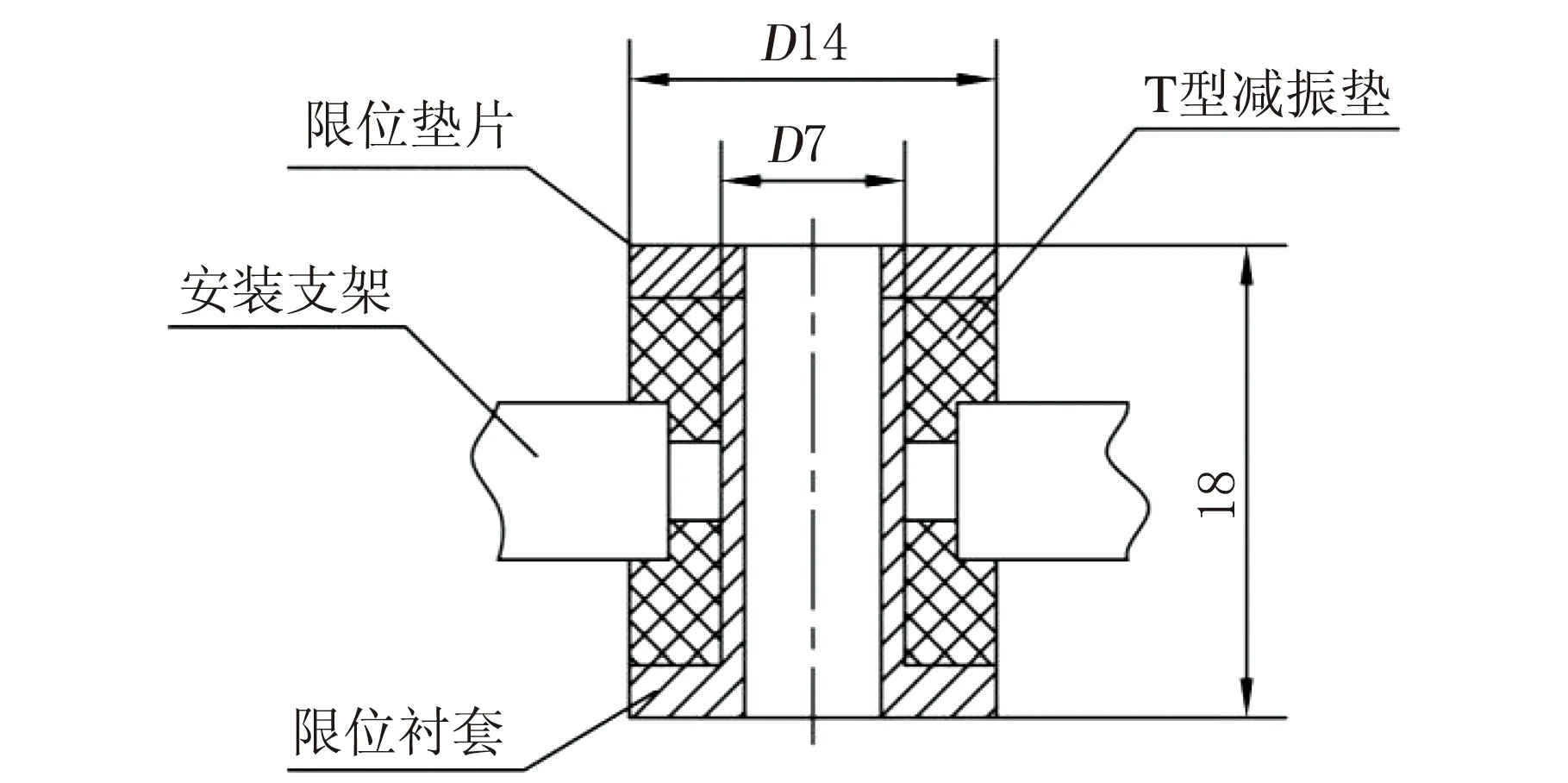
图1 硅橡胶减振器结构示意图
通常真实电子设备的刚度值较大,内部结构复杂,但本文重点关注电子设备作为一个整体的减振分析,因而忽略了其内部结构的影响,对电子设备本身进行了简化处理。简化模型的外形尺寸与真实电子设备相同,开槽以保证模型的质量与真实电子设备的质量相同。硅橡胶减振器分别安装在电子设备的四个角的法兰孔上,均匀布置。硅橡胶减振器采用实体建模,建立的几何模型如图2所示。
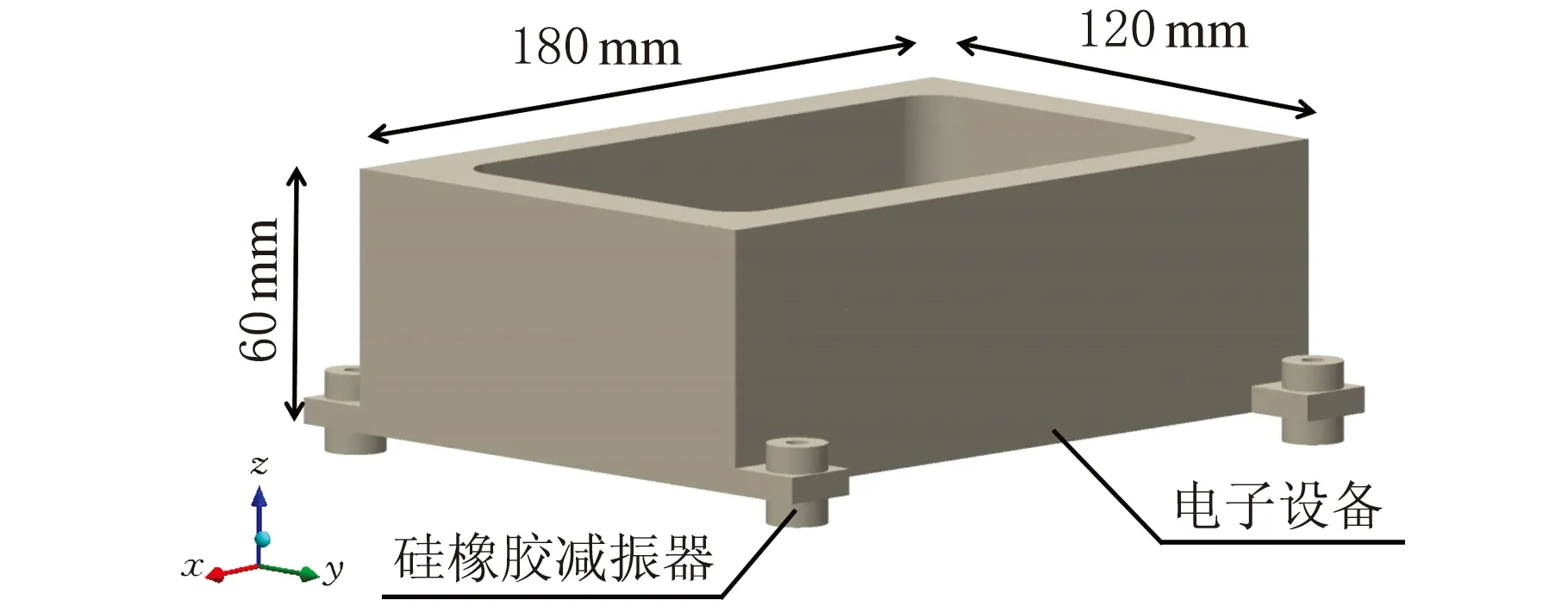
图2 带硅橡胶减振器的电子设备
1.2 材料模型
某电子设备为铝合金材料,硅橡胶减振器的限位垫片和限位衬套为0Cr18Ni9不锈钢材料,材料参数如表1所示。

表1 材料参数
橡胶是一种高分子聚合物材料,其弹性性能与硬度、载荷大小、载荷频率等多种因素有关,应力-应变关系具有明显的非线性,因此不能采用简单的弹性模量描述橡胶的本构关系[15]。一般用应力-应变关系描述其本构关系,由应变势函数对应变不变量的导数来表达[16]。在工程应用中,Mooney-Rivlin超弹性本构模型能够很好地描述橡胶在变形量小于150%时的力学性能[17],其应变能函数如式(1)所示。
(1)
式中:C10、C01为由材料决定的常数;I1、I2为前两阶应变不变量;D1决定材料是否可压缩,J是橡胶材料变形后与变形前的体积比。
通常硅橡胶类材料在受力状态下体积没有明显变化,常假定硅橡胶是不可压缩的[18],即J=1。因此,橡胶材料本构模型的确定关键在于获得C10、C01材料常数。对于单轴压缩实验,橡胶材料的应力与应变关系如式(2)所示。
(2)
式中:σ为应力,MPa;ε为应变。
由式(2)可知,通过材料的应力-应变关系,便可采用最小二乘法拟合确定材料参数C10、C01。对于天然橡胶,可根据橡胶的硬度由经验公式求得材料参数C10、C01,但是其准确性相对较低,因此要获得相对准确的材料参数仍需要具体的材料力学实验来确定。
本文采用的橡胶为某型硅橡胶,其近似为不可压缩材料,可按Mooney-Rivlin超弹性本构模型模拟,用于表征硅橡胶的弹性;硅橡胶的阻尼系数用于表征硅橡胶的黏性。本文针对某型硅橡胶进行了单轴压缩实验,将得到的载荷-位移数据转化为应力-应变数据,得到的单轴压缩实验数据如表2所示。
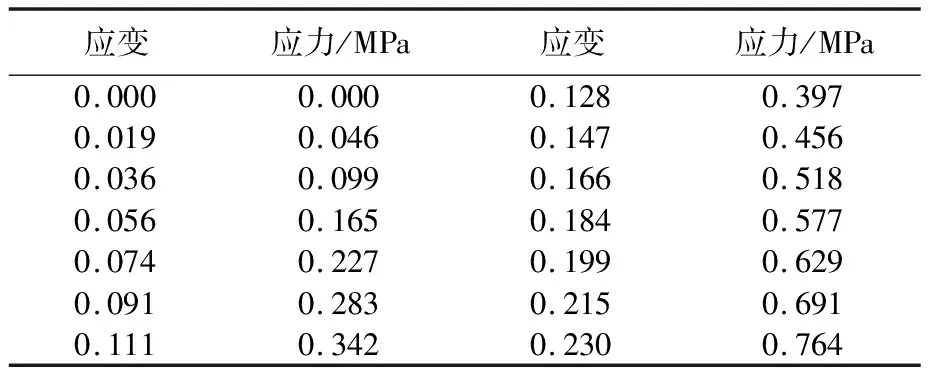
表2 单轴压缩实验数据
基于单轴压缩实验获得的应力-应变数据,采用最小二乘法识别硅橡胶Mooney-Rivlin本构模型参数。进一步地,采用Mooney-Rivlin本构模型的拟合数据和实验数据如图3所示,从图3可以看出,该本构模型与实验数据拟合度较好。经过计算,拟合值与试验值残差的方差Q为0.000 3,Q越小表明误差越小,即拟合的精度越高。因此,拟合得到的Mooney-Rivlin本构模型可用于后续的有限元分析。
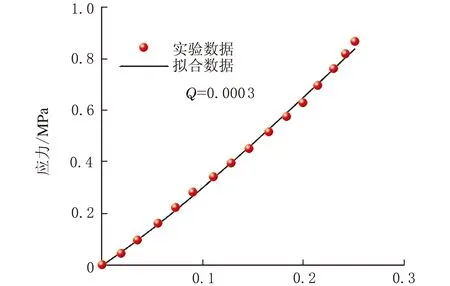
应变
1.3 网格模型
考虑到六面体单元精度较高,整个电子设备系统均采用六面体单元划分网格,通过控制网格划分器的参数来保证模型网格的均匀性,划分后的网格模型如图4所示,整个模型单元数为48 010个。硅橡胶减振器与电子设备之间采用螺钉紧固连接,考虑到有限元计算的规模和时间,在有限元分析过程中采用共节点连接。

图4 网格模型
1.4 载荷与边界条件
直接频率响应分析的载荷为频率10~2 000 Hz的单位加速度。在频率响应的基础上进行随机振动分析,随机振动条件如表3所示,X、Y向输入均方根7.6 g的功率谱密度函数,Z向输入均方根3.8 g的功率谱密度函数。

表3 随机振动条件
根据实际工况,以Z向为例进行说明,其边界条件为约束硅橡胶减振器限位垫片以及限位衬套X、Y、Z三个方向的转动自由度和X、Y方向的平动自由度,只释放Z向的平动自由度。X向和Y向边界条件设置同理。
1.5 求解设置
采用MSC Patran/Nastran软件对安装橡胶减振器的电子设备进行频率响应分析以及随机振动分析。为了提高计算效率,采用非均匀频率步长,即在可能出现谐振频率的10~100Hz频域设置1 Hz的频率步长,而在100~2 000 Hz频域设置38 Hz的频率步长。
2 振动实验
为了验证频率响应有限元分析的合理性,需要对带硅橡胶减振器的电子设备进行X、Y、Z三个方向的振动实验。
振动实验系统主要由信号放大、功率放大器、激振器、振动实验台、测量传感器、控制传感器等组成。电子设备通过实验夹具固定在振动实验台上。实验时,信号放大器将信号传给功率放大器,经过功率放大器放大的信号传输给激振器,使振动实验台产生振动,最终将振动载荷通过实验夹具传递给电子设备。在实验夹具上安装控制传感器,在电子设备的顶部中心黏贴测量传感器,以保证和有限元分析中提取结点的位置一致。通过将控制传感器与测量传感器输出结果进行对比,得到电子设备的谐振频率与加速度传递率。振动实验系统如图5所示。
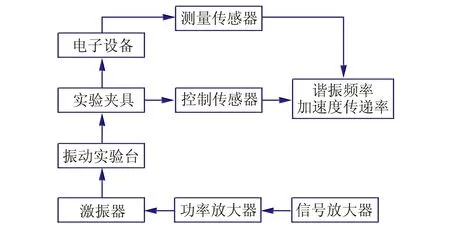
图5 振动实验系统示意图
3 结果与讨论
3.1 频率响应分析
选取电子设备顶部中心处的节点进行结果分析,图6为电子设备减振处理后X、Y、Z三个方向的频率响应曲线。由图6可知,谐振频率处加速度传递率最大,谐振频率之后的频段,加速度传递率迅速下降,说明橡胶减振器的减振效果很明显,具有明显的阻尼效应。X向的谐振频率为62 Hz,加速度传递率为3.4;Y向的谐振频率为62 Hz,加速度传递率为3.4;Z向的谐振频率为71 Hz,加速度传递率为3.7。
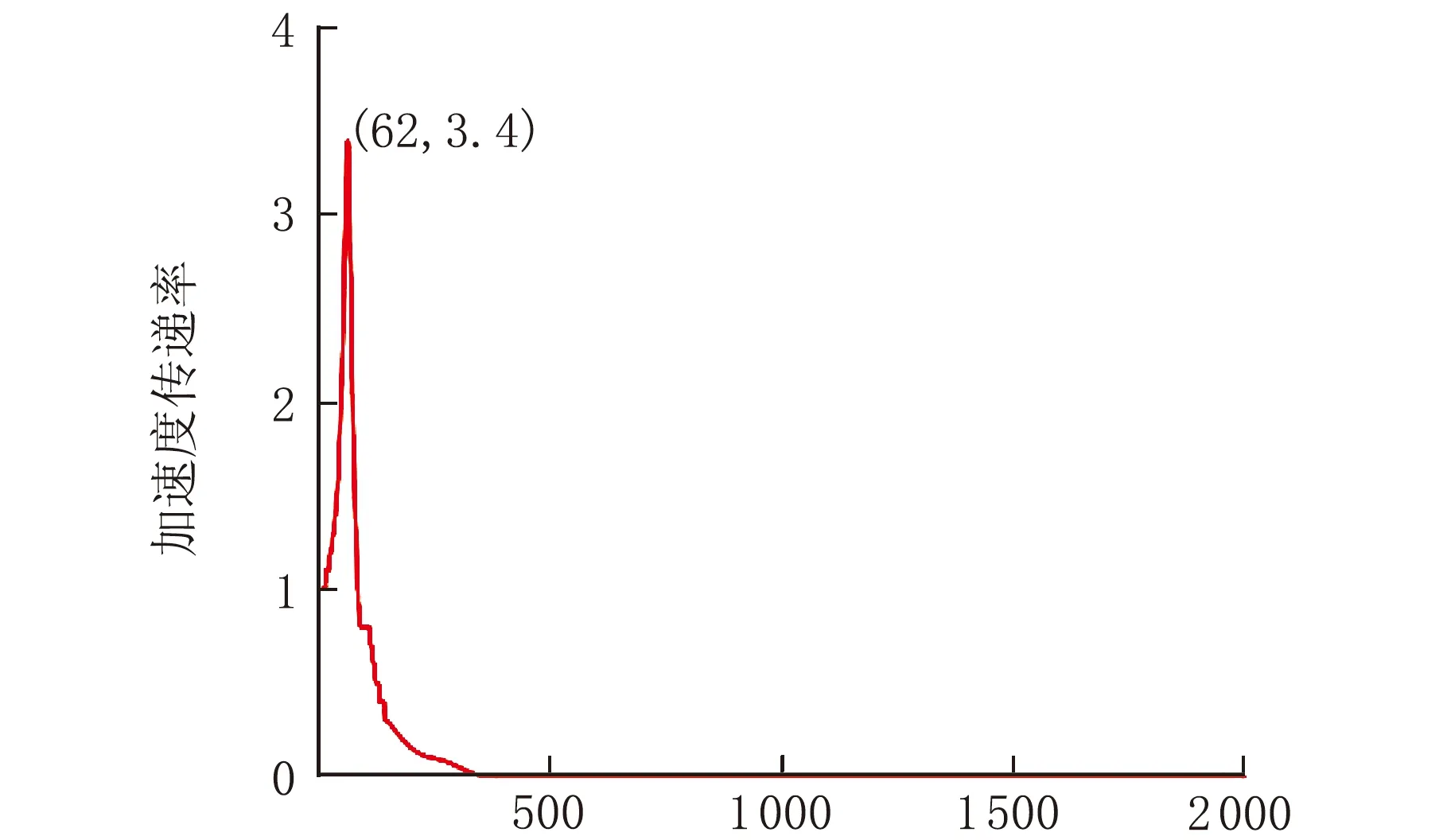
频率/Hz
3.2 振动实验与频率响应分析结果对比
将振动实验结果与频率响应分析结果进行对比,如表4所示。由表可知,电子设备经过硅橡胶减振器减振后,X、Y、Z三个方向的加速度传递率均在4以下。
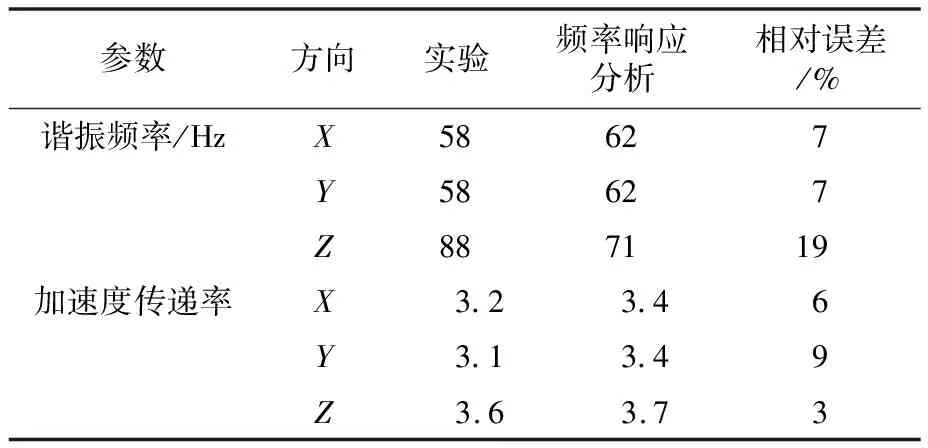
表4 实验结果与频率响应分析结果对比
频率响应分析结果与实验结果基本吻合,谐振频率的相对误差小于20%,加速度传递率的相对误差小于10%,其中,X、Y方向的谐振频率以及加速度传递率误差均小于10%。
由于实际硅橡胶减振器的特性参数随频率变化,而本文采用的阻尼系数为固定值,导致实验结果与有限元分析结果有一定的误差。但上述误差在工程可接受范围之内,在一定程度上验证了有限元分析的准确性,说明本文建立的非线性有限元模型可用于后续的随机振动分析。
3.3 随机振动分析
选取电子设备顶部中心处的节点进行结果分析,图7为X、Y、Z三个方向上随机振动的功率谱密度(PSD)响应曲线,其中RMS为均方根值(有效值),这里指振动加速度峰值。由图7可知,经过硅橡胶减振器减振后的电子设备在X、Y向的随机振动PSD响应曲线基本一致,可以说明橡胶在X、Y向的刚度以及减振效果一致。

频率/Hz
X向随机振动环境的输入均方根为7.6 g,电子设备顶部中心位置的输出均方根为2.8 g,减振效率达到63%;Y向随机振动环境的输入均方根为7.6 g,电子设备顶部中心位置的输出均方根为2.9 g,减振效率达到62%;Z向随机振动环境的输入均方根为3.8 g,电子设备顶部中心位置的输出均方根为1.6 g,减振效率达到58%。相比Z向的减振效率,X、Y向的减振效率更好,均达到60%以上。
4 结 论
(1)建立了硅橡胶的Mooney-Rivlin超弹性本构模型,该模型与实验数据拟合程度较好,拟合值与实验值残差的方差Q为0.000 3。
(2)频率响应分析计算结果与实验结果基本吻合,相对误差最大不超过20%,验证了硅橡胶减振器非线性有限元模型的准确性和有效性,可为类似橡胶减振器结构的设计计算提供参考。
(3)某电子设备经过硅橡胶减振器减振后,X、Y、Z三个方向的加速度传递率均在4以下,随机振动的减振效率均大于50%,减振效果明显。
