大视场红外经纬仪分区误差修正方法研究*

2022-11-12张琦周瑜张晓明迟明祎衣冰

现代防御技术 2022年5期

张琦，周瑜，张晓明，迟明祎，衣冰

（1. 中国人民解放军63861 部队，吉林白城 137001；2. 中国人民解放军32183 部队，辽宁锦州 121000）

0 引言

光电经纬仪是重要的靶场光电测量设备，主要用于各类导弹外弹道测试、卫星等航天器发射和测控任务［1-2］，具有大口径宽视场、高跟踪和识别能力的优势［3］，而大视场红外经纬仪的全视场测角精度是重要的技术指标。光电经纬仪光学系统的特性决定了在光学经纬仪的视场中，偏离主点位置的像素成像都存在不同程度的径向畸变、偏心畸变、焦平面变形，尤其是短焦距大视场的红外成像系统［4-5］，为后续的图像处理和数据解算带来不希望的误差，须对其进行校正。理想的误差修正方法是对视场中每个点进行采集和误差修正，但显然并不符合实际，工程实践通常采用分区域处理方法，以红外视场按照5 行×7 列均匀分割成35 个区域为例，在每个区域内采集多个点，以被测目标真值为基准进行最小二乘拟合，得到所在区域的测角修正系数组，模型点数量不同修正精度不同，为了追求较高精度，模型点的数量可根据具体需求增加。传统的经纬仪误差修正方法多以平行光管（或方位标）的全站仪测量真值作为基准，对经纬仪编码器值和相面坐标解算得到的指向角与真值之间的差值进行最小二乘计算，实现对大视场光学经纬仪或拼接弹道相机的分区误差修正。笔者在长期的实践中发现，以经纬仪完全对准目标时的经纬仪指向值代替平行光管真值作为基准，进行分区最小二乘拟合得到的修正模型能够进一步提高经纬仪的测角精度。为了验证结论的有效性，分别采用传统的依托真值误差修正方法和本文提出的依托指向值的误差修正方法建立了2 类修正模型，分别拍摄并解算同一平行光管的测量值，进行对比实验验证。

1 合成角度计算

1.1 轴系误差及其修正

光电经纬仪的结构可归纳为“三轴两盘一面”。“三轴”是指竖轴线（也叫垂直轴线）、横轴线（也叫水平轴线）和视轴线（也叫视准轴线）［6-7］；“两盘”是指方位角度盘和俯仰角度盘［6］；“一面”即像面，具体指感光器件的上表面。

经纬仪测角的数学原理是构建在理想的经纬仪机械结构基础上的，理想化的三轴、两盘、一面的几何关系如下［6］：

（1）竖轴线须竖直，即竖轴线必须与水平面垂直；

（2）横轴线须垂直竖轴线，即横轴线与水平面平行；

（3）视轴线须垂直横轴线；

（4）两个度盘满足精度要求；

（5）视轴穿过像面中心并与像面垂直；

（6）像面坐标系的x 轴与竖轴垂直，y 轴与横轴垂直。

而由于加工、装调等因素影响，理想机械机构在现实中并不存在［8］，所以在对经纬仪进行定期标校过程中需要对经纬仪实际光机结构偏离上述理想结构的角量，也就是影响视轴定向的单项差进行解算，本文主要从视轴误差、零位误差、横轴误差和定向误差这4 个主要误差项展开修正方法研究。

1.1.1 视轴误差

视轴误差［9］是指视轴线不垂直于横轴线的角量，也叫作照准差，用c 表示。视轴误差对经纬仪视轴定向精度的影响，在俯仰角E ＜65°，主要为方位方向，可由式（1）［9］表示：

式中：E 为被测目标的俯仰角；ΔAc为由c 产生的方位测角误差。

视轴误差的计算方法：用设备度盘分别以正镜和倒镜瞄准俯仰角为0 的无穷远目标（在外场拍方位标），由方位编码器读得方位角Az和Ad，则视轴误差为［10］

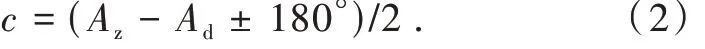
1.1.2 零位误差

零位误差［10］是指当视轴指向水平方向时，俯仰编码器的读数（角量），用h 表示。零位误差对经纬仪视轴定向精度的影响，主要表现在俯仰方向，可由式（3）［10］表示：

式中：ΔEh为由h 产生的俯仰定向误差。

零位误差的计算方法：以正倒镜分别瞄准水平位置上的无穷远目标（在外场拍方位标），由俯仰编码器读得俯仰角Ez和Ed，则零位误差为［10］

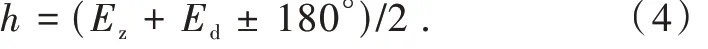
1.1.3 横轴误差

横轴误差［10］是指横轴线不垂直于竖轴线的角量，称为水平轴误差，用b 表示。横轴误差对视轴定向精度的影响，在俯仰角E ＜65°时，主要表现为方位方向，可表示为［10］

式中：E 为被测目标的俯仰角；ΔAb为由b 产生的方位定向误差。

横轴误差的计算方法：分别以正镜和倒镜测量俯仰角为30°～65°的无穷远目标（在外场拍北极星），由方位编码器读得方位角Az和Ad，则横轴误差为［10］

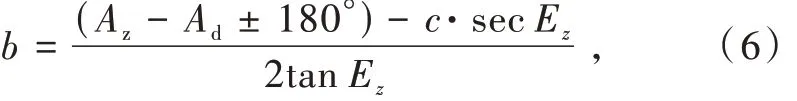
式中：Ez为目标正镜俯仰角测量值。

1.1.4 定向误差

定向误差［11］是指方位编码器零位线与规定零位线的不一致性，用g 表示。定向误差对视轴定向精度的影响，主要表现为方位方向，可表示为［10］

式中：ΔAg为由g 产生的方位定向误差。

定向误差计算方法：分别以正镜和倒镜测量俯仰角为0 的无穷远目标（在外场拍方位标），由方位编码器读得方位角Az和Ad，则定向误差为［12］

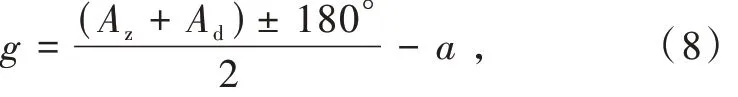
式中：a 为目标的理论角度。

1.2 合成角度的计算

宽视场光学经纬仪目标方位角、俯仰角的计算模型［3］为

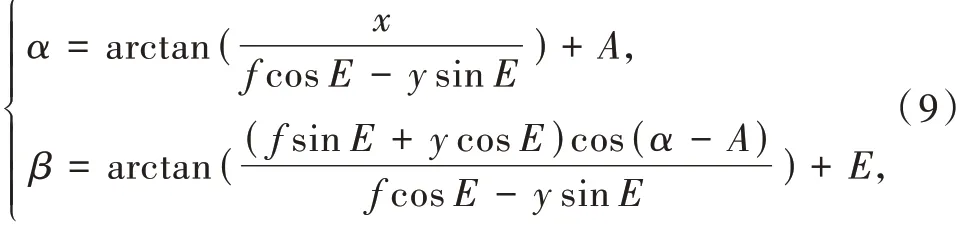
式中：α 为经纬仪测角的方位角；β 为经纬仪测角的高低角；x 为水平方向的像面坐标；y 为垂直方向的像面坐标；f 为经纬仪主距；A 为经纬仪视轴的方位角；E 为经纬仪视轴的高低角。

2 分区误差修正方法

2.1 分区误差修正方法基本思想和算法步骤

分区误差修正处理方法的基本思想［4-5，13］是：当经纬仪对同一目标测量时，无论目标成像在像面的任何位置，理论上经纬仪解算出的角度应该是一致的，但在实际测量中，测量的像面坐标与理论的像面坐标存在偏差，分区误差修正就是要对像面坐标的偏差进行修正，其基本算法步骤为：

（1）将靶面分割为M×N 个小区域。

如图1所示，红外视场按照5×7分割成35个区域。

图1 5×7 红外分区误差修正打点图Fig.1 Dot chart of angle measurement error correction for 5×7 infrared segmented area

（2）在每个区域内采集足够多的样点并计算指向角。

（3）采取最小二乘法［14-15］计算每一个区域内经纬仪对点目标的成像位置的偏差修正系数。

（4）建立分区误差修正模型。

算法流程如图2 所示。

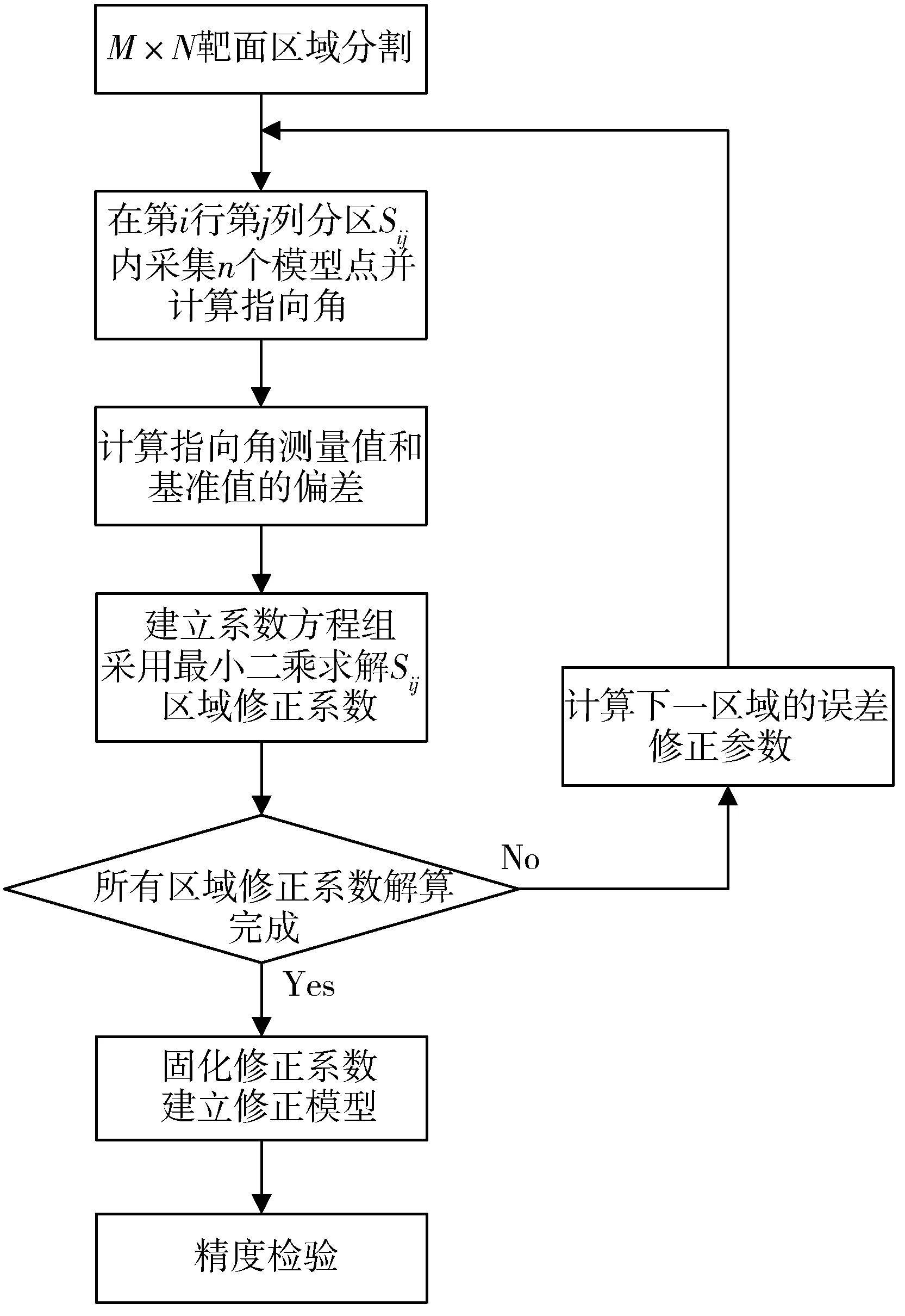
图2 分区误差修正方法流程图Fig.2 Flow chart of angle measurement error correction method of segmented area

点目标的像面坐标的理论值［3］如下：

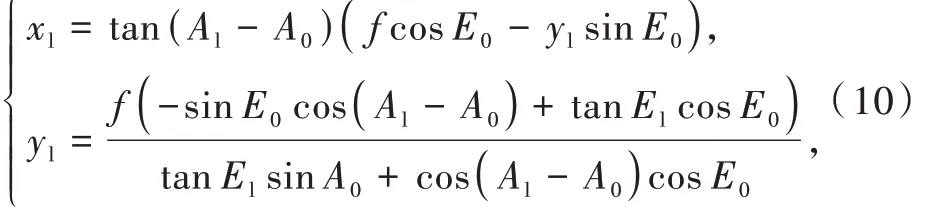
式中：xl、yl为点目标在该小区域像面坐标值的理论值；Al、El为点目标相对于经纬仪成像中心的方位角和俯仰角的理论值；A0、E0为经纬仪视轴对空方位角和俯仰角，即方位俯仰编码器值，通过经纬仪控制软件读出；f 为经纬仪主距。

假设实际像面坐标为x、y，修正后的像面坐标是为x'、y'，采用线性修正，线性修正的公式为

式中：k1、k2、k3为水平 x 方向像面坐标修正系数；k4、k5、k6为竖直 y 方向像面坐标修正系数。

假设在每个小区域对同一点目标（平行光管）采集 n 次测量，则

假设每个点的像面坐标理论值为（XLi，YLi），则min，根据多元函数极值原理，将式（12）对 k1、k2、k3取偏导数，并令其为0：

即

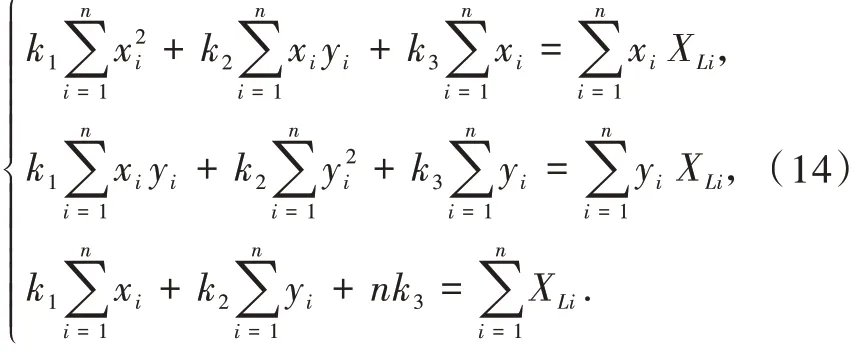
式（14）为水平方向的系数方程组，同理，竖直方向的系数方程组为

求解式（14），（15），即可求出该区域的6 个修正系数。

2.2 依托真值的分区误差修正方法

传统的依托真值的分区误差修正方法在进行区域修正系数计算时，以平行光管的相对真值（AT，ET）为计算理论像面坐标的基准，即：

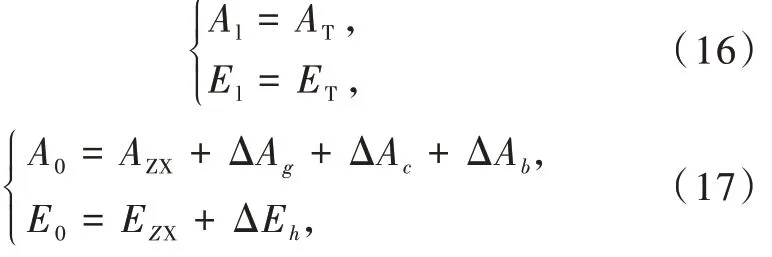
式中：Al、El为点目标相对于经纬仪成像中心的方位角和俯仰角的理论值；A0、E0为经纬仪对点目标的方位角和俯仰角的实测值；AZX、EZX为经纬仪的指向值即编码器示数；f 为经纬仪主距；ΔAg、ΔAc、ΔAb、ΔEh如前文表述，分别表示视轴误差g、零位误差c、横轴误差b、定向误差h 对经纬仪测角精度带来的误差值。

将式（16）、（17）代入式（10）中，解算得到点目标的理论像面坐标值xl、yl，将理论像面坐标值xl、yl和样点实测像面坐标值x、y 带入式（12），通过求解方程组（14）、（15），得到 k1、k2、k3、k4、k5、k6为该区域的修正系数。同理，最终可得到M×N 个区域的修正系数组。

2.3 依托指向值的分区误差修正方法

为了进一步提升大视场红外经纬仪全视场测角精度，相比于传统的依托真值的经纬仪误差修正方法，本文提出依托经纬仪完全对准平行光管时的经纬仪指向值作为光学标校基准的分区误差修正方法：调整经纬仪光轴指向平行光管，通过经纬仪伺服系统调节像面中心和目标的相对位置，反复调节直至目标和成像中心之间的像面脱靶量ΔA=0，ΔE=0，以此时编码器值也就是相面脱靶量为0 时的经纬仪指向值（AZ0，EZ0）代替平行光管真值作为计算理论像面坐标的基准，即

将式（18）代入式（10），解算得到点目标的理论像面坐标值 xl、yl，将理论像面坐标值 xl、yl和样点实测像面坐标值 x、y 带入式（12），通过求解方程组（14）、（15），得到 k1、k2、k3、k4、k5、k6为该区域的修正系数。同理，最终可得到M×N 个区域的修正系数组。

3 实验验证及误差分析

3.1 实验验证

为了证实本文提出的依托指向值的分区误差修正方法能够提升经纬仪测角精度，分别以依托真值和依托指向值构建各自的修正模型，开展精度对比实验，以视场角约为2°的某型红外经纬仪3 台分站为研究对象。

首先，将全视场按照4×4 进行分区，以0°平行光管为基准，以全站仪测量结果为理论真值，分别按照依托真值和依托指向值的方法，求解修正系数组，分别写入2 套目标提取程序中，除6 个参数外，确保其他变量相同。

然后，对另一个平行光管进行多次动态测量，分别按照以上2 套修正方案求解指向角。

最后，将2 套修正方案计算得到的指向角与全站仪测得的平行光管相对真值比较，最终获得方位和俯仰测角精度结果如表1 所示。

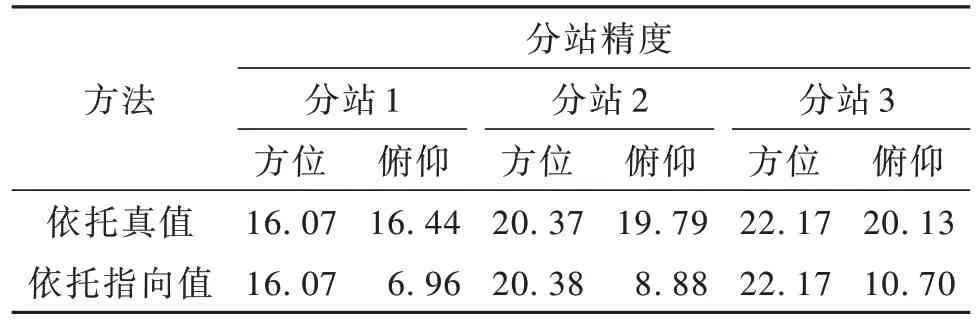
表1 测角精度比对Table 1 Angle measurement accuracy comparison（″）

图3 和图4 所示为方位方向和俯仰方向2 种方法的测角精度比对。

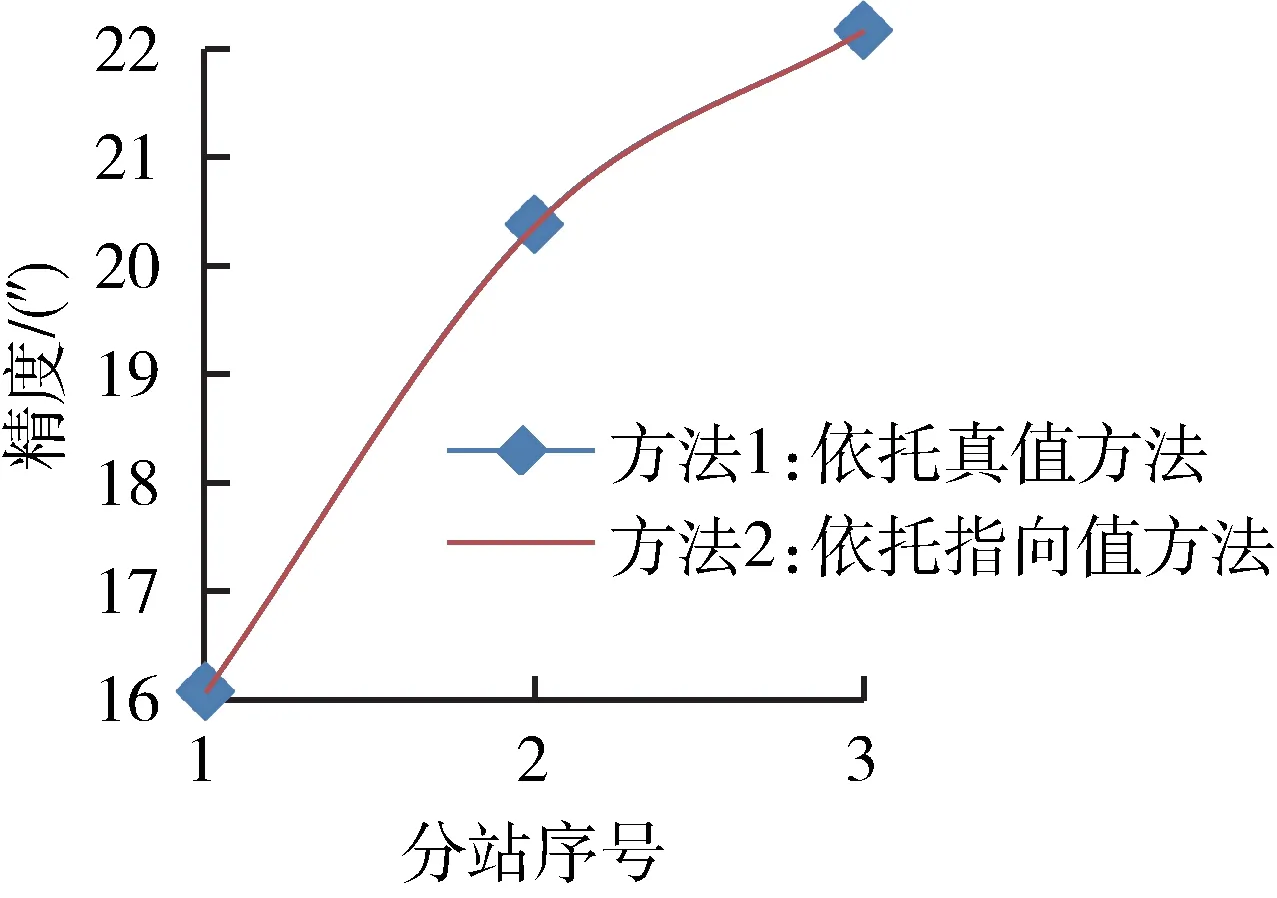
图3 方位测角精度比对Fig.3 Accuracy comparison of azimuth angle measurement

图4 俯仰测角精度比对Fig.4 Accuracy comparison of pitch angle measurement

从数据比对的结果来看，在俯仰方向的测角精度比对中，方法2 优于方法1，方法1 的误差为方法2的误差近2 倍大小，但在方位方向的测角精度比对中，2 种方法基本一致。

3.2 误差分析

对可能导致上述对比结果的原因进行分析：在理想情况下，经纬仪不存在影响视轴定向的单项差，则

即2 种方法测得的修正系数是一致的，测角精度结果也应该是一致的。但在实际测量中，由于存在零位误差、照准误差、定向误差、横轴误差等误差，导致修正系数不一致，从而测量精度不一致。在此次实验中，使用0°光管作为计算修正系数的基准，所以有

则有

由式（21）可知，方位方向的修正系数基本一致，因而2 种方法的方位测角精度结果基本一致，也就是图3 所示的2 种方法前提下经纬仪的测角精度几乎相同的原因；而对于俯仰方向，ET与EZ0并不相近，导致在2 种方法俯仰方向上的修正系数有明显差异，从而俯仰测角精度表现较大差异。

依托真值的分区修正方法计算得到的修正系数，与当次测量的轴系误差有关，而在经纬仪的实际使用过程中，事前须对定向误差、照准误差、零位误差进行标定，每次的标定结果并不完全一致，因此采取依托真值的分区误差修正方法忽视了每次事前拍标的三差的差异性，尤其是在经纬仪使用时间达到一定年限时，单次拍标的三差结果呈现更为明显的差异性。相比之下，依托指向值分区修正方法计算得到的修正系数，能够把每次拍标三差结果的差异性都考虑在内，因而会得到更好的测角精度。

综上，在使用分区处理方法对大视场经纬仪进行像面坐标修正时，使用依托指向值测得的修正系数，会得到更好的测角精度。