一种非协作通信信号调制方式识别方法*

薛德鑫，单涛，董士军，张进

（1. 江苏自动化研究所，江苏 连云港 222061；2. 北京理工大学，北京 100081）

0 引言

随着控制技术、计算机技术、材料技术及通信技术的成熟，无人化作战得到快速发展，并逐渐成为世界新军事革命重要发展方向，陆续出现空中无人系统、陆上无人系统及海上无人系统［1］，同时涌现出比如集群作战、跨域协同作战、有人/无人协同作战等众多新作战概念，给现代防御技术体制、方式方法等带来不小的冲击。然而纵观现代及可预见未来的无人化作战可以发现其共性特点是高度依赖通信技术，如文献［2］指出“通信链路是无人机的生命链和作战效能发挥的保障链”，实际上对陆上无人车、海上无人艇来说也是一样的，无人系统执行任务时必须利用通信技术实现信息分发共享、指令接收等必要功能，因此，通信对抗往往被作为防御无人化作战的切入点，而非合作通信信号识别作为防御链路的探测识别环节为后续跟踪、打击、指挥决策提供依据，成为了通信对抗领域的研究热点。

目前，通信对抗领域已经出现了很多信号识别的方法，典型的如基于特征参数提取的识别方法［3-6］，基于星座图的识别方法［7-10］，基于高阶累积量的识别方法［11-15］。其中，基于星座图的识别方法计算复杂，且要求在相干接收的情况下工作，并需要一定的先验信息。而基于高阶累积量的识别方法对频偏非常敏感，如果信号未被搬移到基带（含有载波）将可能导致识别失败，且该算法同样需要进行大量的计算。基于特征值的调制方式识别计算量小，对载波频率估计误差不敏感，在非协作通信中，为缺少先验知识的通信信号识别提供了可能，因此，目前基于特征的识别方式是信号识别主流方法［16］。

鉴于上述背景并结合目前无人系统常用通信信号调制方式，本文提出了一种非协作通信信号调制方式的识别方法，利用信号处理算法对信号进行特征参数提取，结合判决流程对信号调制方式进行自动识别，可以识别的调制信号类型包括AM、ASK、2FSK、4FSK、BPSK、QPSK、16QAM、64QAM 等，与利用星座图、高阶累积量识别方法相比，该方法运算量小，且对信号频偏不敏感，不会因为信号存在频偏导致识别失效。

1 信号识别方法理论

本文提出的非协作通信信号调制方式识别方法，默认在采集带宽内仅存在单一未知调制类型信号。

已调制信号统一数学模型表示为

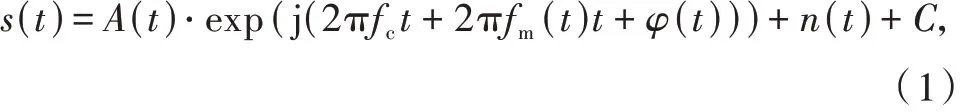
式中：t 为时间；fc为调制信号载波频率；A(t)，fm(t)，φ(t)均为时间的函数，其中A(t)为信号瞬时幅度，对应幅度调制，fm(t)为基带信号的瞬时调制频率，对应频率调制，φ(t)为瞬时相位，对应相位调制，除对应调制制式外，以上函数对于其他调制制式均视为常数；n(t)为噪声；C 为直流常量。

1.1 预处理

接收到的已调制信号中的载波、直流分量等都会对后续调制识别产生不利影响，因此需要对信号进行预处理并提取包络，具体过程如下：

（1）去载波

将已调制信号搬移到基带成为基带信号，搬移过程表示为

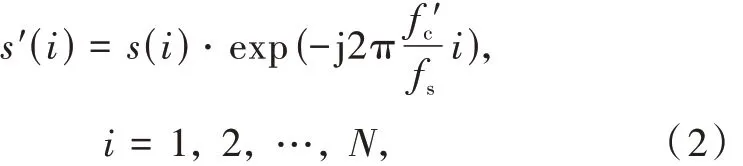
式中：fs为信号采样率；fc'为估计的信号载波频率；s(i)为信号采样序列；s'(i)为去载波后的信号；N 为采样点数。

（2）去直流

为了避免信号中的直流分量对后续特征提取造成不利影响，需对采样信号进行去直流处理，去直流的过程也可以称为“零中心”处理。默认通道内仅含有高斯白噪声，故噪声均值为0 dB，因此，采样信号取平均后仅含有直流信号，去直流过程即减去采样数据的均值，可以表示为

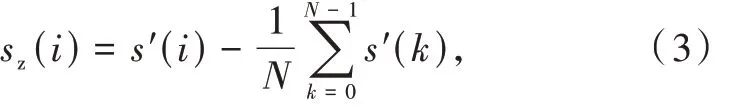
式中：sz(i)为去直流后的信号。

（3）包络归一化

使不同信号的幅值能够收敛在同一量纲中，方便后续的特征参数提取。包络归一化过程表示为

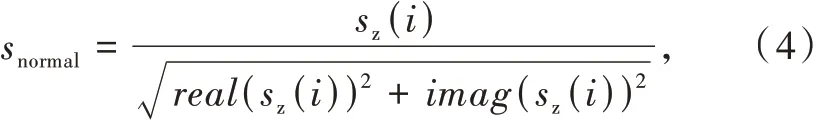
式中：Snormal为通过预处理后得到了零中心包络归一化的基带信号。

1.2 频谱最大值系数识别法

频谱最大值系数即为归一化后信号频谱的最大值，其数学表达式为

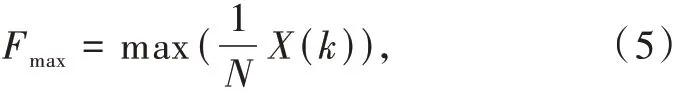
式中：X(k)为零中心包络归一化后信号的离散傅里叶变换后的谱线。因离散傅里叶变换结果各点的幅值与傅里叶变换点数有关，因此需要除以N 将参数标准化，使最终结果与傅里叶变换点数无关。

AM 为模拟调制，与其他数字调制信号相比，其能量集中，体现在频谱上即在中心频率处有最大谱峰，其谱峰峰值最高，因其为双边谱信号，故大部分能量平均分布在2 个谱峰上，理想情况下，其Fmax参数应在0.5 附近。ASK 在包络归一化后，会丢失调制信息，近似于连续波信号，其Fmax参数值与AM 近似。2FSK 信号能量均匀分布在2 个载波上，所以其参数应在0.25 附近。同理4FSK 应在0.125 附近。因此该参数可以将调幅信号区分出来。

1.3 瞬时幅度一阶绝对原点矩识别法

零中心归一化瞬时幅度的一阶绝对原点矩，由文献［17］提出，符号表示为Env，该参数的数学表达式为

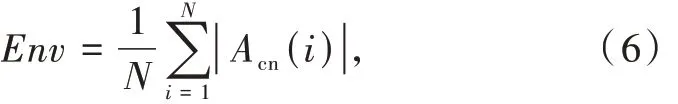
其中，

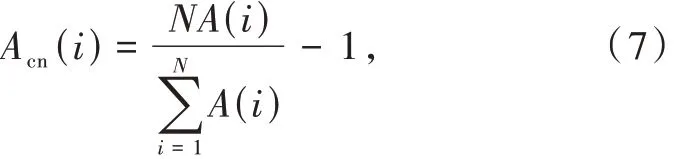
式中：A(i)为零中心包络归一化的基带信号瞬时幅度。

该参数能够反映出信号包络变化情况，ASK 信号因键控存在，包络变化最为剧烈，而AM 信号为恒包络信号，包络稳定。MPSK 和MQAM 信号存在相位调制，会出180°相位跳变，这会使信号包络存在瞬态过零的点，因此包络不稳定，MFSK 信号可以认为是恒包络信号，包络稳定。故该参数既可以区分AM 和 ASK 信号，也可以区分 MPSK、MQAM 和 MFSK信号。

1.4 单频分量凸显度识别法

信号的单频分量凸显度Cn为信号功率谱的最大值与其两边特定范围内谱线均值的比值，用来反映功率谱线最大值的凸显程度，其数学表达式为

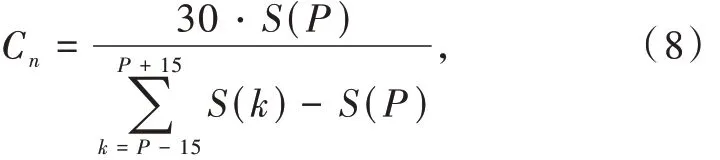
式中：S(k)为零中心包络归一化后信号的功率谱；P 为谱线最大值的位置；Cn的下标n 表示该参数是由信号的n 阶谱得到。因MPSK 信号的M 次方可以恢复出信号的载频信息，所以在M 倍载频处会有比较明显离散冲击谱线。

BPSK 在二次方谱和四次方谱中存在离散冲击谱线，QPSK 在四次方谱中存在离散冲击谱线而在二次方谱中不存在冲击谱线，16QAM 信号无论在二次方谱还是在四次方谱中均不存在冲击谱线，因此通过信号的Cn可以分辨出BPSK、QPSK 和16QAM等信号。

1.5 16QAM 与 64QAM 信 号 的 区 分 法

对于 16QAM 与 64QAM 的区分，文献［18］提出了基于2 种调制方式幅度分布的C 参数，即统计2 种调制方式幅度大于幅度均值的点与小于幅度均值的点的比值进行识别。具体计算过程为

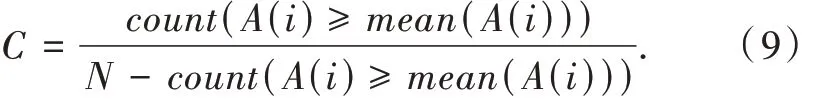
但是利用幅值的分布特性受噪声影响很大，在信噪比较低情况下该参数并不具备理想的识别性能。

考虑到64QAM 调制信号存在52 种相位，16QAM 仅存在12 种相位，其包络稳定度存在明显差别。因此同样可以利用前述Env 参数与C 参数结合，进行综合判定，提高识别准确率。

1.6 2FSK 与 4FSK 信 号 的 区 分 法

文献［17，19］都提出了定义为非弱信号段上的零中心归一化瞬时频率绝对值的一阶绝对中心距作为识别2FSK 和4FSK 的特征参数，但是该特征参数需要准确的载波估计和码速率估计，且计算较为复杂。

考虑到FSK 为频移键控存在频率跳变，如图1所示即为2FSK 和4FSK 的归一化瞬时频率图，2FSK存在二相频率跳变，4FSK 存在四相频率跳变，因此本文提取包含频率特征的基带信号相位差构建新的信号，具体如下：

（1）对于调频信号，经过预处理后可表示为

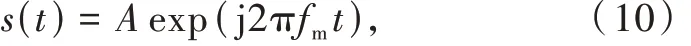
式中：fm为基带信号的瞬时调制频率。

（2）提取2 个相邻采样点间基带信号相位差的处理方法表示为

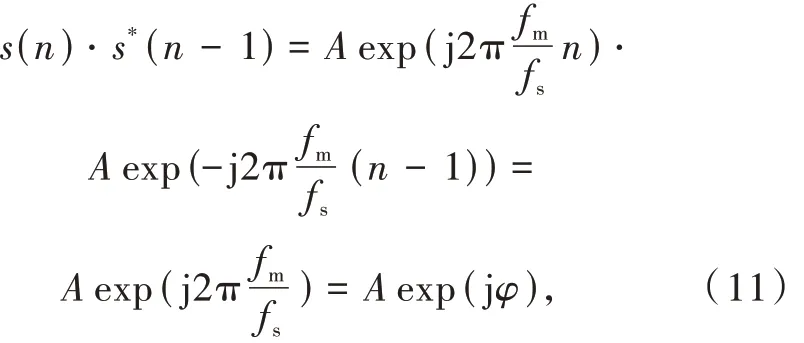
式中：s(n)为第n 个采样点基带信号；s*(n - 1)为第n - 1 个采样点基带信号的共轭；φ 为采样点间基带信号相位差。

以信号采样点间的相位差作为实部，将采样点间的相位差值倒序作为虚部来构建新的信号，那么对于2FSK 信号来说，新信号具有四相位，即为QPSK 信号，对于4FSK 信号来说，新信号具有16 个不同幅值和相位，即为16QAM 信号，新构建的信号利用本文1.4 节中描述的单频分量凸显度即可区分出 2FSK 和 4FSK 信号。

2 识别流程

根据前述信号调制方式识别方法论基于判决树理论，给出信号调制方式识别流程，如图2 所示。

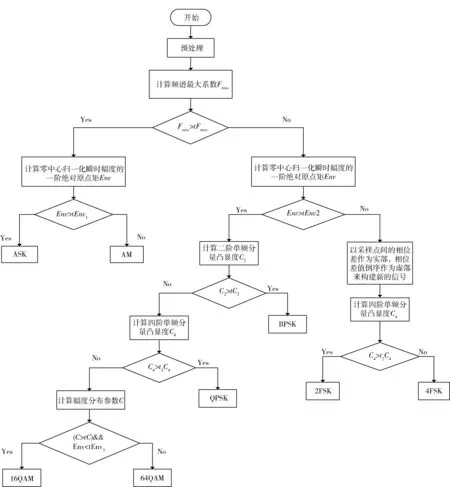
图2 信号调制方式识别流程Fig.2 Signal modulation mode identification process

信号经过预处理后，先计算信号的频谱最大值系数Fmax，如果大于阈值tFmax则认为信号属于ASK/AM 这一集合，否则属于PSK/FSK 集合。

无论信号属于哪个集合，均需计算零中心归一化瞬时幅度的一阶绝对原点矩Env。对于ASK/AM集合内的信号，如果参数Env 大于阈值tEnv1则可直接判断信号为ASK 信号，否则为AM 信号。而对于PSK/FSK 集合内的信号，如果参数Env 大于阈值tEnv2，则可判断该信号属于PSK 类信号，否则属于FSK 类信号。

对于PSK 类信号，先计算二阶谱和四阶谱单频分量凸显度C2、C4，如果二阶谱单频分量凸显度C2大于阈值tC2，则可以直接判断信号属于BPSK 调制。如果二阶谱参数小于阈值而四阶谱单频分量凸显度C4大于阈值t1C4，则可判断信号为QPSK 调制。如果均不满足，则计算幅度特分布征参数C，如果该参数大于阈值tC，则可以判定为16QAM 调制，否则为64QAM 调制，在判断时，还可用零中心归一化瞬时幅度的一阶绝对原点矩进行辅助判断。

对于FSK 类信号，对采集的信号进行错一位的共轭相乘，并求相角、相角作为实部，其倒叙作为虚部构成新的信号，对新信号求四阶谱单频分量凸显度C4，如果该参数大于阈值t2C4，则可判断该信号为2FSK 信号，否则为4FSK 信号。识别流程完成。

本文提及的所有阈值可通过第3 章仿真结果曲线获得，具体为根据仿真结果曲线，选取合适的信噪比，在该信噪比下选取特征参数阈值，确保其能够将各信号所对应特征参数曲线分隔开，则该值可作为对应信号的特征参数阈值。

3 仿真校验

为了使仿真贴近真实情况，认为频率估计存在误差，所有预处理后的信号残留有200 kHz 载波，信噪比范围从0 dB～30 dB。在Matlab 仿真环境下，各特征参数在不同信噪比下对于不同调制信号的对应曲线如图3 所示。

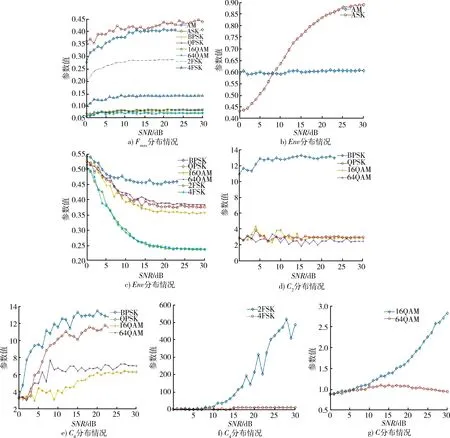
图3 各特征参数对各调制信号识别性能Fig.3 Identification performance of each characteristic parameter to each modulation signal

Matlab 模拟产生不同调制类型信号各1 000 组，并加入不同信噪比噪声，验证本文提出识别方法的识别率，识别率如图4 所示。

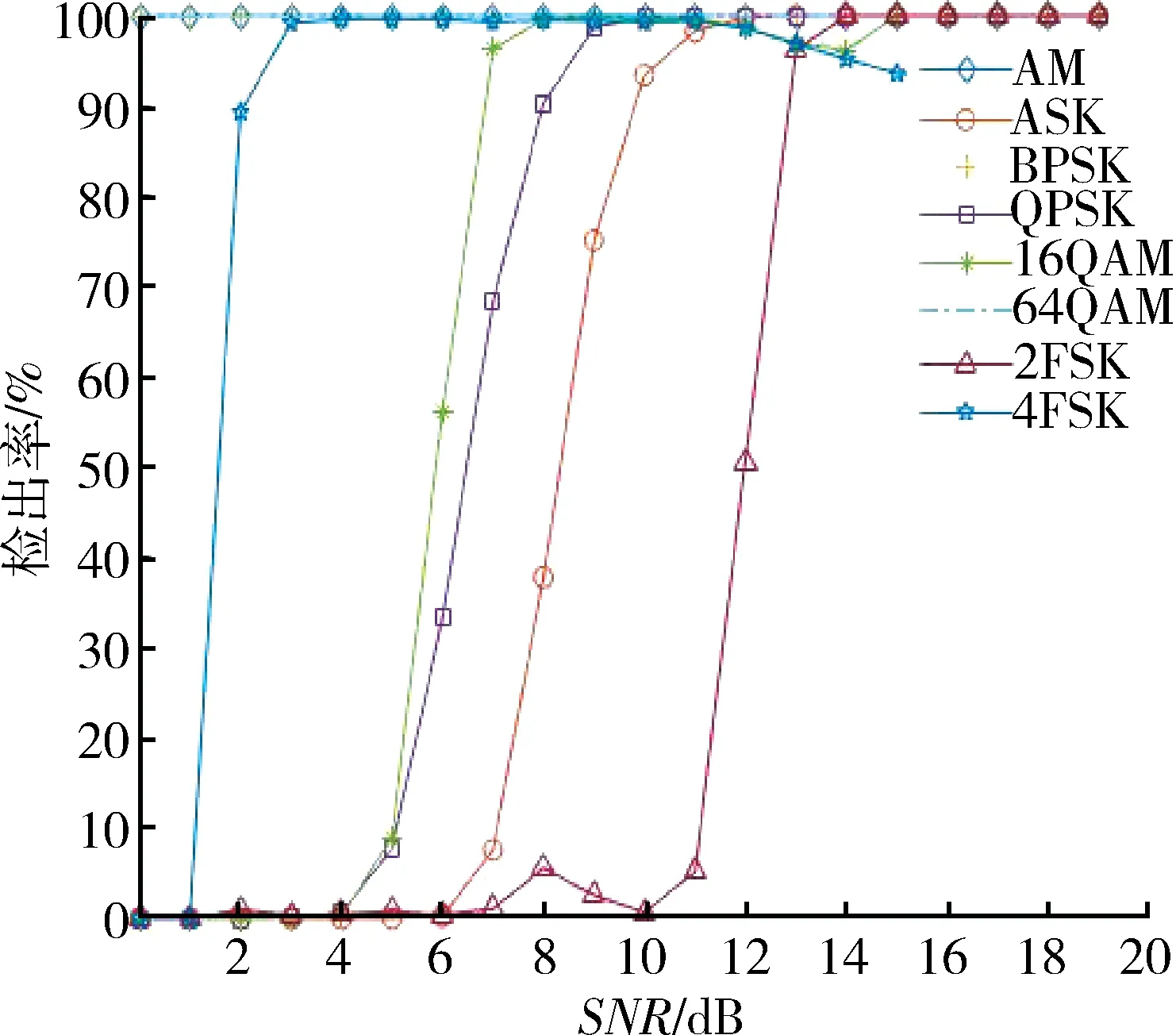
图4 不同信噪比下各调制信号的检出率Fig.4 Detection rate of each modulated signal at different SNR

综合以上仿真结果，能够发现本文提出的识别方法在信噪比10 dB 左右时，除2FSK 信号以外的其他信号识别率均达100%，在信噪比提高至12 dB 左右时，所有信号识别率可以保证在95%以上，并且随着信噪比进一步提高，所有信号识别率会进一步提高。

4 结束语

立足于实际需求，本文应用信号处理算法对非协作信号进行特征参数提取，然后以判决树为基础，结合判别流程对信号调制方式进行识别，尤其对于频移键控（FSK）信号，本文通过提取基带信号采样点间相位差构建新的信号，根据构建信号的识别结果反推原信号的调制类型，避免了对先验信息的需求。本文提出的信号识别方法计算简单，更关键的是，对于频偏估计误差有较好的容忍度。根据仿真结果，该方法在信噪比10 dB 左右时，除2FSK信号以外的其他信号识别率均达100%，在信噪比提高至12 dB 左右时，所有信号识别率可以保证在95%以上，具备实际应用于非协作通信中信号快速识别的能力。