大规模风电汇集系统电压不平衡机理、因素及影响规律
2022-11-12刘其辉逄思敏吴林林
刘其辉 逄思敏 吴林林 刘 辉 徐 曼
大规模风电汇集系统电压不平衡机理、因素及影响规律
刘其辉1逄思敏1吴林林2刘 辉2徐 曼2
(1. 新能源电力系统国家重点实验室(华北电力大学) 北京 102206 2. 国网冀北电力有限公司电力科学研究院 北京 100045)
我国风电集中并网地区往往呈现电网结构薄弱、就地负荷小、当地缺乏无功支撑等特点,容易出现电压不平衡现象,严重时导致大量风机脱网,给电网的安全运行带来极大影响。为了分析风电汇集系统电压不平衡产生机理,首先,建立了计及网侧变流器(GSC)、机侧变流器(RSC)及锁相环(PLL)控制环节的双馈风力发电机(DFIG)的基频负序阻抗模型,并由单机模型推广至风电场集群基频负序阻抗模型;然后,基于实际风电汇集系统,构建风电汇集地区负序等效电路,剖析风电汇集地区电压不平衡机理,分析源、网侧主要因素对汇集母线电压不平衡的影响规律;最后,基于Matlab/Simulink仿真平台,验证机理分析及影响规律的正确性。
风电汇集系统 电压不平衡 基频负序阻抗建模 产生机理 影响因素
0 引言
在新能源渗透率不断提高的具有背景下,风力发电凭借着无污染、可再生、装机灵活、运维成本低等优点,迅速在可再生能源发电领域占据重要位置。然而,我国风电集中并网地区往往具有电网结构薄弱、就地负荷小、并网点缺乏无功支撑等特点,易受风电功率时变性和强波动性的影响,容易出现并网地区电压不平衡问题,严重时会导致大量风机脱网,威胁电力系统的安全稳定运行[1]。根据国家标准GB/T15543要求,电力系统中风电汇集系统汇集母线的电压不平衡度长时间不超过2%,短时间不超过4%[2],因此,明确风电机组之间、风电机组与电网之间的相互作用对分析汇集母线电压不平衡的产生机理、找出电压不平衡的主导影响因素具有重要意义。
相较于传统的发生在低电压等级的配电网电压三相不平衡,风电汇集地区的三相电压不平衡主要发生在包括高压线路的风电汇集和送出系统,呈现时空多样性和变化特性,与风电场空间分布、风电出力等有强相关性。目前已有相关文献针对风电汇集系统电压不平衡产生机理及影响因素展开研究。文献[3]指出输电线路的参数不对称是风电经不换位输电线路送出场景下电压不平衡的主要原因;文献[4]分析了输电线路长度、导线排列方式、相序变换及输送电压对电压不平衡的影响;文献[5]对非全线并行架设的高压输电线路空间位置、换位方式等对电压不平衡度的影响展开研究;文献[6]阐明了双极直流微电网电压不平衡的影响机理,指明负载不平衡、线路参数不平衡以及正、负极电源接入不平衡是主要影响因素;文献[7]以牵引变为研究目标,研究牵引变对电压不平衡的影响以及负序补偿策略。然而,上述文献均将研究重点聚焦在输电线路参数、输电线路换位方式及负载参数等网侧因素,未分析风速、风电机组台数、风电场空间分布等源侧因素对电压不平衡的影响。
风电机组作为源侧结构的主要组成部分,其模型的精确建立是研究汇集母线电压不平衡机理分析的基础,其中,在三相不平衡背景下,基频负序阻抗模型尤为重要。文献[8]建立了不平衡电网电压条件下双馈感应发电机(Double-Fed Induction Generation, DFIG)在正、反转坐标系下的完整数学模型;文献[9]在电网电压不平衡以及逆变器滤波电感不平衡的工况下,推导了逆变器输出负序导纳模型;文献[10]通过探究谐波电流与谐波电压之间的关系,提出了适用于稳定性分析的SVG和直驱风机的负序阻抗模型;文献[11-12]建立了风电机组并网负序等效电路,并结合负序等效电路提出了风电机组附加补偿装置进行负序电压补偿的策略。上述研究中,各文献分别建立了DFIG动态模型,逆变器的谐波导纳、阻抗模型,以及不平衡工况下风电机组的优化控制策略,均未进行详细的风电机组基频负序阻抗建模。
综上所述,目前风电汇集系统电压不平衡问题虽然得到了一定的关注,但研究主要集中于线路、负荷等网侧因素对电压不平衡的影响,以及不平衡工况下风电机组的优化控制策略研究,对源侧因素尤其是风电机组自身的控制参数、出力情况、空间分布等对电压不平衡的影响关注较少,未能明确大规模风电汇集地区的三相电压不平衡机理。
为此,本文以我国华北某风电汇集电网为研究对象,建立了计及网侧变流器(Grid Side Converter, GSC)、机侧变流器(Rotor Side Converter, RSC)及锁相环(Phase Locked Loop, PLL)的DFIG基频负序阻抗模型,分析了风电汇集系统母线电压不平衡的机理及主要影响因素,最后基于Matlab/Simulink仿真平台,验证机理分析及影响规律的准确性。
1 风电汇集系统基频负序阻抗建模
1.1 建模思路
实用、准确的双馈风机负序阻抗模型是研究风电汇集系统电压不平衡机理和影响因素的基础和关键。由于DFIG的dq轴电流控制器结构不对称,以及变流器的直流动态耦合特性,在并网点施加某一频率f的电压扰动后,会产生同频率的扰动电流分量和其他频率的耦合电流分量,从而使DFIG存在正、负序耦合阻抗[13-14],电压扰动与电流响应分量的频率关系见表1,其中1代表基频。通过表1可以看出,基频正序的电压扰动只产生基频正序的扰动电流分量,而基频负序的电压扰动会产生基频负序的扰动电流分量以及150Hz正序的耦合电流分量,即DFIG存在正、负序的序间耦合阻抗,且此阻抗表现为序间耦合与频率耦合相结合的形式。
表1 电压扰动与电流响应分量的频率关系

Tab.1 The relationship between voltage disturbance and corresponding component frequency of current
然而,当研究电网稳态电压不平衡情况时,DFIG的阻抗建模只需考虑基频电压、电流之间的特性关系。由上述讨论可知,基频的正序电压扰动无法产生基频的负序电流响应,基频的负序电压扰动也无法产生基频的正序电流响应,因此基频正、负序电压与基频正、负序电流之间不存在耦合关系,即DFIG不存在基频正、负序耦合阻抗。因此本文仅考虑对不平衡有影响的双馈风机基频负序阻抗(以下简称负序阻抗)的建模。
1.2 双馈风机基频负序阻抗模型
双馈风机并网系统结构如图1所示。假设风电机组并网点存在基频负序电压、电流,忽略直流母线电压波动、控制器死区及电力电子器件的开关频率,可将双馈风机等效为GSC和可控DFIG系统(DFIG+RSC)两部分[15]。

图1 双馈风机并网系统结构
1.2.1 锁相环输出角度
实际的风电机组内部控制均在dq坐标系下进行,锁相环负责输出由abc坐标系变化为dq坐标系的角度,因此能否正确表示锁相角是阻抗建模是否准确的基础。锁相环结构框图如图2所示,并网点电压abc经锁相环控制得到包含基频负序电压导致的扰动角Δ的锁相角PLL=1△,其中11为无负序扰动下的锁相角。

图2 锁相环结构框图
基波负序电压对应扰动分量△的频域表达式为

其中


运用锁相环谐波线性化的思想,分析锁相环输出相角与控制环节的线性关系,得到考虑基频负序分量扰动的坐标变换矩阵(PLL),具体表达式见附录。
1.2.2 GSC基频负序阻抗建模
由于网侧变流器的电压控制外环带宽较窄,远小于本文重点研究的基频频段,因此忽略电压外环的影响,考虑基频负序电压对GSC电流调节器输出电流指令值的影响,分析GSC交流侧基频负序电压与基频负序电流的关系,最终得到GSC系统负序阻抗模型如式(3)所示,具体推导过程见附录。

式中,n、n分别为电网基频负序电压、电流分量;为拉普拉斯算子;0和0分别为GSC直流稳态表征量;dq=1为GSC电流环耦合系数,为GSC输出滤波电感;gi(2)=gp+gi/为基频下网侧变流器PI调节器的传递函数;gp、gi分别为PI调节器的比例、积分系数;(2)为基频下锁相环PI调节器的传递函数;1*为电网正序基波电流的共轭。
1.2.3 可控DFIG系统负序阻抗建模
可控DFIG系统的负序阻抗建模采取与GSC阻抗建模相同的思路,其中不同点为转子分量转换到dq坐标轴需要转子位置角r,因此可控DFIG系统坐标变换的基准角度为PLL-r。根据定、转子电流表达式,考虑RSC电流控制环节,整理DFIG定子侧基频负序电压、电流之间的关系得到可控DFIG系统的负序阻抗模型如式(4)所示,具体推导过程见附录。

式中,sn为定子基频负序电流分量;下标s、r分别为定、转子电气量;r0和r0为RSC直流稳态表征量;rdq为RSC电流环解耦系数,rdq=s(r-m2/s),s为定子电角速度,s、r、m分别为定、转子绕组的自感、互感;rd、rq分别为转子电流的d、q轴分量;r1为发电机转子端电流基频正序分量幅值;(2)为基频下锁相环PI调节器的传递函数;ri(2)为基频下转子侧变流器PI调节器的传递函数;n()为负序转差系数;e为发电机定、转子匝数比。
1.2.4 风电机组负序阻抗建模
经过上述分析,双馈风机负序阻抗可以等效为GSC负序阻抗和可控DFIG系统负序阻抗的并联,如图3所示,其具体计算公式为

由式(5)计算得到双馈风机负序阻抗,其验证结果如附图3所示,在不同风况下,两条曲线稳合较好,验证了阻抗模型的准确性。
1.3 风电场及风电场集群基频负序阻抗模型


图4 风电场基频负序阻抗模型
单一风场的负序阻抗表达式为

本文以我国华北地区具有典型拓扑的某实际风电汇集电网为例进行研究,华北地区某风电汇集系统电气拓扑如图5所示。该汇集系统主要分为三部分:接入220kV汇集母线1的所有风电场(风电场集群1)、接入220kV汇集母线2的所有风电场(风电场集群2)以及外部等效网络,下面讨论两个风电场集群负序阻抗建模过程。

图5 华北地区某风电汇集系统电气拓扑


图6 风电场集群基频负序阻抗模型
根据图6中各风电场阻抗及线路阻抗的串并联关系,推导得到风电集群1和风电集群2的负序阻抗分别为

2 风电汇集系统电压不平衡机理
2.1 风电汇集系统基频负序等效电路
分析风电汇集系统电压不平衡机理,需要考虑激励和响应两方面因素。本文将电网背景不平衡视为激励,将其等效为不平衡电压源;响应则是指在不平衡电压源激励作用下,风电汇集系统产生的不平衡电流和因此导致的系统各节点所表现出来的程度不同的不平衡电压。在激励确定的情况下,响应取决于风电汇集系统的基频阻抗,包括电网、线路、变压器和风电机组的等效阻抗。根据前面分析,风电机组的序间耦合阻抗往往伴随着频率耦合,研究基频稳态不平衡问题,只需考虑其基频负序阻抗。


图7 风电汇集系统基频负序等效电路
2.2 风电汇集系统电压不平衡机理分析
根据GB/T15543,电压不平衡度(Voltage Unbalance Factor, VUF)可表示为[2,18]

式中,1、2分别为三相电压的正、负序分量有效值。
结合图7,推导两条汇集母线的负序电压分量分别为

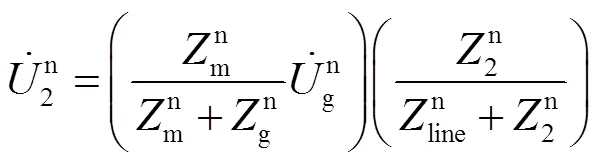
其中

由此可以看出,影响汇集母线基频负序电压的主要因素有电网等效不平衡电压源、电网等效负序阻抗,风电集群1、2的负序阻抗、以及输电线路负序阻抗。其中不平衡电压源作为激励,取决于外部电网的参数与运行情况,本文重点研究负序阻抗对汇集母线负序电压的影响。分别改变、、和,汇集母线2的基频负序电压变化情况如图8所示。

3 电压不平衡影响因素分析
3.1 电源侧影响因素

表2 电源侧主要影响因素

Tab.2 Main influencing factors of power supply side
根据表2可得,电源侧影响因素主要包括风电机组自身控制参数、风速以及风电场内风电机组台数,下面对其影响规律进行进一步分析。
3.1.1 控制参数
除去发电机本体参数,影响单机负序阻抗的参数主要有六个控制参数:pp、pi、gp、gi、rp和ri(见附表1),为了比较不同控制参数对阻抗特性影响的程度,本文采用频域阻抗灵敏度法进行分析,定义双馈风机的负序阻抗灵敏度为[19]

式中,为所要进行灵敏度分析的风电机组控制参数。根据阻抗灵敏度的定义及风电机组的负序阻抗表达式,得到各控制参数的阻抗灵敏度如图9所示。

图9 不同控制参数的负序阻抗灵敏度变化曲线
由图9可知,当参数取值在0.3(pu)~2(pu)范围内,rp的阻抗实部(电阻)、阻抗虚部(电抗)灵敏度远大于其他控制参数的阻抗灵敏度,且负序阻抗实部(负序电阻)、负序阻抗虚部(负序电抗)随rp的增大而增大,其他参数的阻抗灵敏度很小,对负序阻抗影响不大。因此,rp的取值过大,会导致风电机组负序阻抗增大,进而汇集母线电压不平衡度也增大。
3.1.2 风速
DFIG具有在不同风速下实时调整转速以实现最大风能追踪的特点,因此风速是通过影响风电机组转速,导致RSC电流调节环PI调节器的解耦系数rdq以及负序转差系数n发生变化,进而影响风电机组负序阻抗的大小。具体推导过程及转速与风电机组基频负序阻抗的关系图如附图6所示。
假设电网电压不平衡度为5%,各风电场与汇集母线的距离相同,由于源侧因素对汇集母线1、2的影响趋势相同,因此以汇集母线2为例进行分析,绘制不同风速下汇集母线2的电压不平衡度及风电场集群负序阻抗曲线如图10所示。

图10 风速对汇集母线电压不平衡度的影响
由图10可以看出,随着风速的增大,汇集母线2的电压不平衡度减小并趋于稳定。结合式(5)可以分析得出:随着风速的增大,风电机组的转速在启动区和最大风能追踪区增大,之后在恒转速区和恒功率区保持稳定,因此风电场的负序阻抗也会随着转速的增大而减小,后趋于稳定。
然而,风电汇集系统包含多个风电场,风电场与风电场之间的距离相差较远,风速存在较大差异,将风电场集群等值为同一风速、同一距离下的风电场不具有普遍性。因此将汇集母线2的风电集群按距离汇集母线的远、近分为远、近端风电场两部分,具体划分标准见附表2,电气拓扑如图11所示。

图11 远、近风场拓扑
保持场外汇集母线长度等其他影响参数不变,仅改变远、近端风场风速,重点对比远、近端风场的风速变化对汇集母线电压不平衡度的影响程度大小。绘制风速与汇集母线2的电压不平衡度三维图如图12所示。
为了比较分析不同位置风场在风速变化量相同时对汇集母线电压不平衡度的影响大小,取图12中边界曲线AP、AQ,将其投影到二维坐标系中,得到如图13所示的远、近风场风速对汇集母线电压不平衡度的影响。

图12 远、近端风场运行于不同风速下的汇集母线电压不平衡度三维曲面

图13 远、近风场风速对汇集母线电压不平衡度的影响
由图12、图13可得,随着远、近端风场风速的增加,等同于减小风电场基频负序阻抗,汇集母线电压不平衡度均减小,且呈非线性关系,但近端风场风速变化时电压不平衡度变化量更大。
3.1.3 风电机组台数
在实际工程中,风电场的风电机组台数大多不相同。本文通过改变风电机组台数模拟风电场投入运行的风电机组数量以及风电场输出功率的变化,根据实际风电场输出功率进行折算,主要研究台数变化范围为100~400台,对应风电集群输出功率为1 500~6 000MW。风电场集群内风电机组台数变化对汇集母线电压不平衡度的影响如图14所示。
由图14可知,随着风电机组台数的增加,风电场输出功率不断增大,风电场集群基频负序阻抗呈非线性减小趋势,汇集母线2的电压不平衡度也不断减小。
下面讨论远、近风电场风电机组台数变化对汇集母线电压不平衡度的影响。假设近端风电场风电机组台数为1,远端风电场的风电机组台数为2。绘制远、近端风场风电机组台数与汇集母线2电压不平衡度三维图如图15所示。

图14 风电机组台数对汇集母线电压不平衡度的影响

图15 远、近端风场风电机组台数与汇集母线电压不平衡度三维曲面图
同样将图15中的BM、BN曲线投影到二维坐标系下得到风电机组台数对汇集母线电压不平衡度的影响如图16所示。

图16 风电机组台数对汇集母线电压不平衡度的影响
由图15、图16可以看出,随着远、近端风电场风电机组台数的不断增加,等同于减小风电场基频负序阻抗,汇集母线电压的不平衡度均不断减小,但近端风电场的影响更大。
3.2 电网侧影响因素
表3 电网侧主要影响因素

Tab.3 Main influencing factors of power grid side
3.2.1 电网强度
DFIG接入交流电网的强弱通常采用系统等值电抗值或短路比表示。系统等值电抗越小,短路比越大;系统等值电抗越大,短路比越小[20-21]。短路比表达式为

式中,n为系统额定电压;B为系统等值阻抗;G为单台风机容量。
保持风速为13m/s,改变系统等值电抗值从0.5(pu)至1(pu),对应的电网短路比为3.834~3.109,绘制汇集母线2的电压不平衡度变化图如图17所示。

图17 系统等值电抗变化时汇集母线电压不平衡度变化
由图17可知,保持同一风速下,当系统等值电抗值增大时,即电网短路比减小时,电网等效负序阻抗呈线性增大,汇集母线的电压不平衡度呈近似线性减小趋势。
3.2.2 输电线路长度

图18 输电线路长度变化时基频负序阻抗变化

图19 输电线路长度变化时不同汇集母线电压不平衡度变化
由图18和图19可知,保持同一风速下,当输电线路长度由0.5(pu)增加至2(pu)时,输电线路的负序阻抗线性增加,汇集母线电压不平衡度的变化呈近似线性变化趋势,且汇集母线1的电压不平衡度增大,汇集母线2的电压不平衡度减小,当输电线路长度的改变量相同时,汇集母线2的变化量更大。
4 算例验证
4.1 电源侧因素影响规律验证
4.1.1 控制参数
为了验证上述分析结果的正确性,在Matlab/ Simulink中搭建了如图5所示风电汇集系统的时域仿真模型,原始控制参数见附表1。假设电网电压不平衡度为5%,10s时改变各控制参数的取值,测得汇集母线2的基频负序电压波形如图20所示。
由图20可知,将参数rp从0.6(pu)增加至1.2(pu)时,汇集母线2的基频负序电压明显增大,而调节其他参数时,汇集母线的基频负序电压基本不变,验证了控制参数中rp对三相不平衡影响最大。
4.1.2 风速
保持远、近风场风电机组台数均为200台,系统等值电抗值为1(pu),初始时设定远、近风场风速均为13m/s,7s时分别降低远、近端风场风速至6m/s,汇集母线2的基频负序电压波形如图21所示。

图20 改变控制参数的基频负序电压波形

图21 改变风速的基频负序电压波形
由图21可知,降低远、近风场的风速,汇集母线基频负序电压均增大,但近端风场的风速改变对其影响更大。
4.1.3 风电机组台数
保持风速13m/s不变,系统等值电抗值为1(pu),初始时设定远、近风场的风电机组台数为200台,7s时分别降低远、近端风场风电机组台数至100台,汇集母线2的基频负序电压波形如图22所示。

图22 改变风电机组台数的基频负序电压波形
由图22可知,减少远、近风场风电机组台数,汇集母线基频负序电压增大,但近端风场的风电机组台数改变对其影响更大。
4.2 电网侧因素影响规律验证
4.2.1 电网强度
保持风速13m/s不变,远、近风场风电机组台数均为200台,分别仿真系统等值电抗值为0.5(pu)、0.7(pu)和1(pu),对应的电网短路比为3.834、3.567和3.109时,汇集母线2的基频负序电压变化如图23所示。

图23 改变系统等效电抗的基频负序电压波形
由图23可知,等量增大系统等值电抗值,对应电网的短路比减小,汇集母线基频负序电压呈非线性减小趋势,电压不平衡度减小,验证了上述理论分析的正确性。
4.2.2 输电线路长度
保持风速13m/s不变,分别仿真输电线路长度line为0.5(pu)、1(pu)和1.5(pu)时,汇集母线1、2的基频负序电压波形如图24所示。

图24 改变输电线路长度的基频负序电压波形
由图24可知,成倍增加两风电场集群之间的输电线路长度,汇集母线基频负序电压的变化呈非等比变化趋势。其中汇集母线1的基频负序电压不断增大,相应电压不平衡度增大;而汇集母线2的基频负序电压减小,相应电压不平衡度也减小,且输电线路长度的改变量相同时,汇集母线2的变化量更大,验证了本文理论分析的正确性。
5 结论
为了分析风电汇集系统电压不平衡机理,本文建立了计及GSC及其控制、RSC及其控制以及锁相环的双馈风机基频负序阻抗模型,从负序阻抗角度切入,研究不同元件负序阻抗的改变机理,并基于风电汇集系统基频负序等效电路,分析了源、网侧主要影响因素对汇集母线电压不平衡的影响规律,在一定程度上填补了从源侧因素出发分析电压不平衡机理的研究缺口。
经过分析发现,增大DFIG的RSC电流控制环比例参数rp,减小风电场运行风速,减少风电机组台数及减小系统的等值电抗值均会加剧汇集母线的电压不平衡度,而改变汇集母线之间的输电线路长度对不同汇集母线电压不平衡度的影响不同。本文基于我国华北地区某典型风电汇集电网开展研究,得出的三相电压不平衡规律、影响因素等结论,对于研究其他高比例风电接入电网的三相不平衡问题具有一定的普适性参考价值。本文提出的基于基频负序阻抗模型的分析方法,可为新能源接入电网的电能质量分析和治理提供理论基础。
附 录
1. 风电机组基频负序阻抗建模思路
2.双馈风机并网系统基本电路
根据图1,列写三相静止坐标系下GSC输出电流、电压与并网点电压的关系为

式中,g_abc,i_abc分别为GSC交流侧三相电流、电压;abc为PCC三相电压;为滤波电感。
将式(A1)运用对称分量法进行正、负、零序变换,得到各电压、电流的正、负、零序分量为

式中,下标1、2、0分别代表正、负、零序分量。
时域中a、ga的表达式为



为了后续的简便计算,将式(A3)、式(A4)转换到频域中,得到abc坐标系下PCC电压频域表达式为



abc坐标系下GSC交流侧电流的频域表达式为



3.转换矩阵

其中






4.GSC基频负序阻抗推导过程
由于在风电机组实际运行控制系统中,控制策略均在dq坐标系下进行,因此将式(A8)~式(A10)经式(A11)所示变换矩阵,变换得到GSC交流侧电流的dq分量。


GSC电流调节器的控制框图如附图1所示,图中gd、gq分别为dq轴电流实际值;gd_ref、gq_ref分别为d、q轴电流参考值;gd_ref、gq_ref分别为变流器输出的d、q轴电压参考值。

附图1 GSC电流调节器控制框图
App.Fig.1 GSC current regulator control block diagram
当系统处于稳态时,基频正序电流可以稳定跟随电流参考值,而对于基频负序电流,风电机组未附加负序抑制策略时,其电流参考值为0,因此含有基频正、负序分量的GSC侧电流通过电流调节器,得到变流器输出的d、q轴电压参考值为


式中,0、0分别为GSC输出直流稳态表征量。
将式(A20)和式(A21)经坐标反变换到abc坐标系下,并提取a相电流表达式(A22)代入式(A1)中,推导得到0、0表达式式(A23)。


将式(A23)代入式(A2)中,整理得到GSC系统输出基频负序电压与基频负序电流的关系为
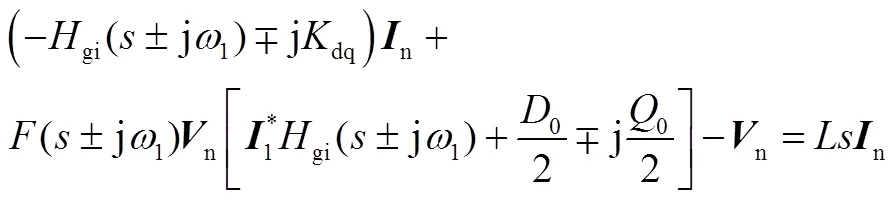
根据计算电路中电流的流向以及电压的方向,GSC系统的负序阻抗可以整理为电压比电流的形式,如式(3)所示。
5.可控DFIG系统基频负序阻抗推导过程
abc坐标系下发电机(电动机惯例)电压方程、磁链方程分别为

式中,、、分别为电压、电流、磁链矢量;ss、sr、rs、rr分别为折算到定子侧的发电机定、转子的自感矩阵、互感矩阵;s、r分别为折算到定子侧的发电机定、转子绕组的电阻。
采用对称分量法将式(A25)变换为正、负序形式,即

式中,s_pn、r_pn分别为正、负序表示的电压,s_pn=[spsn]T,r_pn=[rprn]T;s_pn、r_pn分别为正、负序表示的电流,s_pn=[spsn]T,r_pn=[rprn]T;s_pn、r_pn分别为正、负序表示的磁链,s_pn=[spsn]T,r_pn=[rprn]T。
由于发电机定、转子之间存在转差,频域中转子各分量的频率会变化为转差频率,同时坐标变换矩阵中的角度变化为PLL-r,故可将频域中转子三相电流表达式写为
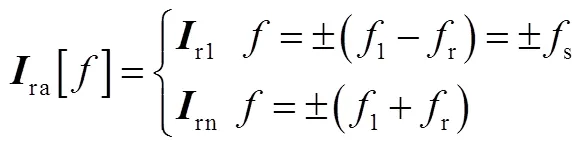



由于双馈风机系统中,转子分量转换到dq坐标轴下比定子分量多出转子位置角r,因此受控DFIG系统坐标变换的基准角度为PLL-r。建立坐标变换矩阵(PLL-r)为

其中






RSC电流调节器的控制框图如附图2所示。图中,ri()=rp+ri/为RSC电流环PI调节器的传递函数,rp、ri分别是PI调节器的比例、积分系数;rdq=s(r-m2/s)为RSC电流环解耦系数,s=1-r;rd、rq分别为转子d、q轴电流实际值;rd_ref、rq_ref分别为转子d、q轴电流参考值;rd_ref、rq_ref分别为RSC变流器输出的d、q轴电压指令值。

附图2 RSC电流调节器控制框图
App.Fig.2 RSC current regulator control block diagram
将旋转坐标系d轴定于电网电压矢量方向,采用恒幅值坐标变换将式(A27)~式(A29)变换到dq坐标下为


系统运行于稳态时,附图2中d、q轴直流电流参考值与实际值之差为零,此时RSC电流调节器输出电压指令值为直流量r0、r0,基频负序电流指令为0,考虑PLL的影响,由附图2可得电流调节器输出的电压指令值为
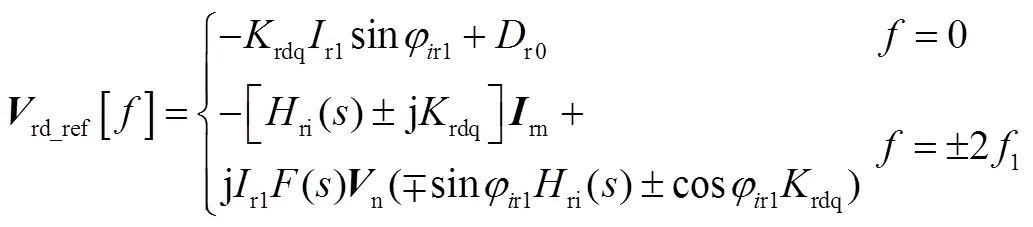

下面求解直流量r0、r0的值。dq坐标系下采用电动机惯例的发电机电压方程、磁链方程为

式中,为微分算子;s_dq、r_dq分别为定子、转子绕组的d、q轴电流;s_dq、r_dq分别为转子绕组的d、q轴电压;s_dq、r_dq分别为dq坐标系下的定、转子磁链;s、r及m分别为dq坐标系下折算到定子侧的发电机定、转子的自感矩阵和互感矩阵。
机组运行于稳态时,系统各基频分量为恒定值,因此式(A41)中微分项均为0。整理式(A41)消掉定转子磁链,可得

式中,s_dq=[sdsq]T;r_dq=[r0r0]T;r_dq=[rdrq]T。
整理式(A42)可得r0,r0为



频域中负序转差系数为

将式(A26)中消去磁链,整理得基频负序电压、电流关系为



式中,sn=n、sn=n,消去其中rn、rn,代入=j1得可控DFIG系统基频负序阻抗公式如式(4)所示。
附图3 不同风速下双馈风机阻抗模型验证
App.Fig.3 Verification of impedance model of DFIG at different wind speeds
附表1 仿真参数
App.Tab.1 Simulation parameters

参数数值 风力机空气密度/(kg/m3)1.225 切入风速/(m/s)3 切出风速/(m/s)25 额定风速/(m/s)11 叶片半径/m35 桨距角/(°)0 极对数3 发电机额定功率/MW1.5 额定电压/kV0.69 定子电阻RS/Ω0.002 6 转子电阻Rr/Ω0.002 9 定子自感LS/H0.004 907 转子自感Lr/H0.004 845 定、转子互感Lm/H0.004 728
(续)

参数数值 变流器直流电容/μF10 000 开关频率/Hz4 000 直流电压/V1 150 RSC内环电流比例增益Krp0.6 RSC电流内环积分增益Kri8 GSC电流内环比例增益Kgp0.16 GSC电流内环积分增益Kgi1 锁相环比例增益Kpp50 锁相环积分增益Kpi3

附图4 风机转速对基频负序阻抗的影响
App.Fig.4 The influence of fan speed on FFNS impedance
附表2 远、近风场划分标准
App.Tab.2 Standards for dividing far and near wind fields

风电场序号距离汇集母线的距离/km风场分类 817.9近端 971.404远端 1047.087远端 1127近端 1252远端 1334.092近端
[1] 刘辉, 陈璨, 巨云涛, 等. 风电汇-集地区电压不平衡特性分析及抑制策略[J]. 电力系统自动化, 2021, 45(14): 132-139.
Liu Hui, Chen Can, Ju Yuntao, et al. Characteristics Analysis and suppression strategy of voltage unbalance in areas with integration of wind power[J]. Automation of Electric Power Systems, 2021, 45(14): 132-139.
[2] 中国国家标准化管理委员会. GB/T15543—2008 电能质量: 三相电压不平衡[S]. 北京: 中国标准出版社, 2008.
[3] Chen Can, Liu Hui, Wu Linlin, et al. Voltage unbalance mechanism research with large-scale wind power integration[C]//2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, 2019: 1608-1612.
[4] 邹林, 林福昌, 龙兆芝, 等. 输电线路不平衡度影响因素分析[J]. 电网技术, 2008, 32(增刊2): 283-286.
Zou Lin, Lin Fuchang, Long Zhaozhi, et al. Influence factors analysis of unbalance parameter for overhead lines[J]. Power System Technology, 2008, 32(S2): 283-286.
[5] 朱军, 吴广宁, 张龙伟, 等. 非全线并行架设的共用走廊高压输电线路电气不平衡度及其影响因素分析[J]. 高电压技术, 2014, 40(12): 3942-3952.
Zhu Jun, Wu Guangning, Zhang Longwei, et al. Analysis of electrical unbalance degree and its influence factors of multi-circuit transmission lines with partially parallel erection in right-of-way[J]. High Voltage Engineering, 2014, 40(12): 3942-3952.
[6] 杨美辉, 周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2021, 36(3): 634-645.
Yang Meihui, Zhou Niancheng, Wang Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 634-645.
[7] 王辉, 李群湛, 解绍锋, 等. 基于一种新型牵引补偿变压器的牵引变电群贯通供电系统负序补偿[J]. 电工技术学报, 2021, 36(10): 2140-2152.
Wang Hui, Li Qunzhan, Xie Shaofeng, et al. Compensation of interconnected power supply system of traction substation group based on a new type of traction compensation transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2140-2152.
[8] Hu Jiabing, He Yikang. Modeling and enhanced control of DFIG under unbalanced grid voltage conditions[J]. Electric Power Systems Research, 2009, 79(2): 273-281.
[9] 年珩, 杨洪雨. 不平衡运行工况下并网逆变器的阻抗建模及稳定性分析[J].电力系统自动化, 2016, 40(10): 76-83.
Nian Heng, Yang Hongyu. Impedance modeling and stability analysis of grid-connected inverters under unbalanced operation conditions[J]. Automation of Electric Power Systems, 2016, 40(10): 76-83.
[10] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[11] Chen Yinyu, Chen Minwu, Tian Zhongbei, et al. Voltage unbalance management for high-speed railway considering the impact of large-scale DFIG-based wind farm[J]. IEEE Transactions on Power Delivery, 2019, 35(4): 1667-1677.
[12] Suppioni V P, Grilo A P, Teixeira J C. Improving network voltage unbalance levels by controlling DFIG wind turbine using a dynamic voltage restorer[J]. International Journal of Electrical Power & Energy Systems, 2018, 96(Mar.): 185-193.
[13] 刘威, 谢小荣, 王衡, 等. 基于频率耦合阻抗模型的并网变流器全工况小信号稳定性分析[J]. 中国电机工程学报, 2020, 40(22): 7212-7221.
Liu Wei, Xie Xiaorong, Wang Heng, et al. Frequency-coupled impedance model-based small-signal stability analysis of grid-tied converters under all operating conditions[J]. Proceedings of the CSEE, 2020, 40(22): 7212-7221.
[14] 年珩, 徐韵扬, 陈亮, 等. 并网逆变器频率耦合特性建模及系统稳定性分析[J]. 中国电机工程学报, 2019, 39(5): 1421-1432.
Nian Heng, Xu Yunyang, Chen Liang, et al. Frequency coupling characteristic modeling of grid-connected inverter and system stability analysis[J]. Proceedings of the CSEE, 2019, 39(5): 1421-1432.
[15] 杨洪雨. 双馈异步发电机系统阻抗建模及稳定性分析[D]. 杭州: 浙江大学, 2016.
[16] 陈鹏伟, 戚陈陈, 陈新, 等. 附加频率控制双馈风电场频率响应特性建模与参数辨识[J]. 电工技术学报, 2021, 36(15): 3293-3307.
Chen Pengwei, Qi Chenchen, Chen Xin, et al. Frequency response modeling and parameter identification of doubly-fed wind farm with additional frequency control[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3293-3307.
[17] 陈昆明, 马成斌. 基于DIgSILENT的风电场等值建模研究[J]. 电气技术, 2020, 21(4): 15-19, 75.
Chen Kunming, Ma Chengbin. Research on wind farm equivalent modeling based on DIgSILENT[J]. Electrical Engineering, 2020, 21(4): 15-19, 75.
[18] Bollen M. Definitions of voltage unbalance[J]. Power Engineering Review IEEE, 2001, 21(5): 49-51.
[19] 李杨, 帅智康, 方俊彬, 等. 灵敏度在变换器系统阻抗稳定性分析中的应用[J].中国电机工程学报, 2021, 41(10): 3480-3491, 3673.
Li Yang, Shuai Zhikang, Fang Junbin, et al. Application of sensitivity in impedance-based stability analysis for converter systems[J]. Proceedings of the CSEE, 2021, 41(10): 3480-3491, 3673.
[20] 谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366-2372.
Xie Xiaorong, Liu Huakun, He Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems[J]. Proceedings of the CSEE, 2016, 36(9): 2366-2372.
[21] 徐海亮, 吴瀚, 李志, 等. 低短路比电网下含负序控制双馈风机稳定性研究的几个关键问题[J]. 电工技术学报, 2021, 36(22): 4688-4702.
Xu Hailiang, Wu Han, Li Zhi, et al. Several key issues on stability study of DFIG-based wind turbines with negative sequence control during low short-circuit ratio power grids[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4688-4702.
The Mechanism, Factors and Influence Rules of Voltage Imbalance in Wind Power Integration Areas
Liu Qihui1Pang Simin1Wu Linlin2Liu Hui2Xu Man2
(1. Key Lab of Power Systems with Renewable Energy Sources North China Electric Power University Beijing 102206 China 2. State Grid Jibei Electric Power Company Limited Research Institution Beijing 100045 China)
The centralized integration of wind power in China often shows the characteristics of weak grid structure, small local loads, and lack of local reactive power support, which easily leads to voltage unbalance. In severe cases, a large number of wind turbines can be disconnected from the grid, which can greatly impact the safe operation of the power grid. In order to analyze the forming mechanism of voltage unbalance in large-scale wind power integration area, firstly, the fundamental frequency negative-sequence (FFNS) impedance model of doubly-fed induction generator (DFIG) including grid side converter (GSC), rotor side converter (RSC) and phase locked loop (PLL) is established. In addition, the single machine FFNS impedance model is extended to the wind power cluster; Secondly, taking one actual wind power integration area as the research target, the negative sequence equivalent circuit of the wind power integration system is constructed, the voltage unbalance mechanism of the wind power integration area is proposed, and the main influencing factors from both source side and grid side, together with their affecting rules are analyzed in detail. Finally, based on the MATLAB/Simulink simulation platform, the validity of the mechanism analysis and influence law is verified.
Wind power integration areas, voltage unbalance, fundamental frequency negative-sequence impedance, forming mechanism, influencing factors
10.19595/j.cnki.1000-6753.tces.211447
TM614; TM712
国家电网公司科技项目资助(4000-202014051A-0-0-00)。
2021-09-13
2021-12-21
刘其辉 男,1974年生,博士,副教授,研究方向为双馈风电机组并网运行及控制。E-mail:liuqihuifei@163.com
逄思敏 女,1998年生,硕士研究生,研究方向为双馈风电机组并网运行及控制。E-mail:476673746@qq.com(通信作者)
(编辑 赫蕾)
