低温环境下锂离子电池荷电状态与超声透射飞行时间的关系研究

吴立峰 刘 昊 林仲钦 徐 策 马国明

低温环境下锂离子电池荷电状态与超声透射飞行时间的关系研究

吴立峰 刘 昊 林仲钦 徐 策 马国明

（新能源电力系统国家重点实验室（华北电力大学） 北京 102206）

为掌握低温下锂离子电池荷电状态（SOC）与超声检测特征量之间的关系，开展了圆柱卷绕型锂离子电池荷电状态超声检测与理论分析。设计了一种超声换能器固定装置来提高超声信号检测的稳定性和灵敏度。建立特征提取算法，提取超声信号幅值和超声飞行时间两个特征参量，获得低温环境下锂离子电池的最大可用容量。结果表明，在低温环境下，超声飞行时间特征量相较于超声信号幅值特征量能更准确地反映锂离子电池的荷电状态。该文还研究了低温对锂离子电池负极材料弹性模量、质量、长度的影响，建立了低温环境下锂离子电池荷电状态与超声透射飞行时间量化方程，量化方程与检测数据之间的拟合决定系数为0.966 8。该研究可为低温环境下锂离子电池SOC的准确检测提供参考。

低温 锂离子电池 荷电状态 超声透射方法 超声信号幅值 超声飞行时间

0 引言

锂离子电池在便携式电子产品、新能源汽车和储能电站等领域被广泛使用[1-2]。锂离子电池的荷电状态（State of Charge, SOC）是表征电池健康状况的重要指标[3-5]，但低温对锂离子电池材料有较大影响，导致电池容量显著下降，因此开展低温环境下锂离子电池荷电状态的准确检测十分必要[6-8]。

锂离子电池的荷电状态是指在特定放电条件下，电池剩余容量占额定容量的百分比。目前对锂离子电池SOC的检测方法主要有开路电压法、内阻检测法、安时积分法和基于智能优化算法的等效电路模型等方法[9-12]。申彩英等在室温下对18650磷酸铁锂电池进行充放电试验，采集不同SOC下的开路电压，获得了开路电压与电池SOC之间的关系[13]。杨文荣等提出通过建立电池等效模型检测电池初始SOC，提高了基于安时积分法的电池SOC检测精度[14]。梁培维等基于数据驱动方法，在室温下对锂离子电池进行放电试验，记录电池的欧姆电阻与放电容量，并以三次样条插值算法建立他们之间的关系来检测电池SOC[15]。宫明辉等在建立电池二阶RC电路模型的基础上提出模糊自适应扩展卡尔曼滤波器算法，提高了算法收敛速度，相较于传统卡尔曼滤波算法对锂离子电池SOC在线实时检测更具有实用性[16]。

上述研究方法存在检测速度慢、只能离线测量、等效电路难以反映电池内部物理化学过程等问题，因此国内外学者开始探索运用超声检测技术来检测锂离子电池的荷电状态。

华中科技大学黄云辉教授课题组基于超声检测法开展了锂离子电池负极析锂等现象的研究，并基于检测结果预测电池寿命[17-19]。马里兰大学M. Pecht教授课题组对容量急剧衰减和完好的同一种棱柱形锂离子电池进行超声检测，发现容量急剧衰减后的电池接收到的超声信号幅值（Signal Amplitude, SA）更低[20]。维尔茨堡大学G. Sextl教授课题组对方形软包锂离子电池进行超声检测，发现超声透射信号中，慢纵波的信号幅值、超声飞行时间（Time of Flight, TOF）与电池的容量密切相关[21]。普林斯顿大学D. A. Steingart教授课题组对方形软包锂离子电池进行超声检测试验，结果表明，在锂离子电池充电时，TOF不断降低，SA不断增大；放电时则相反[22]。普林斯顿大学K. W. Knehr教授课题组运用超声波透射技术对经过几百个循环后的方形软包锂离子电池进行试验研究，提取了超声飞行时间和信号幅值，结合端电压数据通过机器学习的方法构建SOC预测模型[23]。

综合国内外研究现状分析，目前超声检测锂离子电池荷电状态方法存在以下不足：①试验均在室温环境下进行，然而低温对锂离子电池SOC造成显著影响，该方法能否实现低温下SOC检测尚未可知；②研究对象多为棱柱形和方形软包锂离子电池，对于复杂结构的圆柱卷绕型锂离子电池研究较少，超声在圆柱卷绕型锂离子电池内部传播衰减大，很难检测；③运用超声信号特征量检测锂离子电池荷电状态时，缺乏超声透射飞行时间与锂离子电池荷电状态及温度的量化关系，难以基于超声透射飞行时间结果计算不同温度下的锂离子电池荷电状态。

为解决上述问题，本文在-20～10℃环境下搭建了圆柱卷绕型锂离子电池荷电状态检测试验研究平台，开展了超声透射方法在低温环境下对SOC检测的可行性研究，建立了低温环境下锂离子电池荷电状态与超声透射飞行时间的量化方程，确定了其中的关键参数。本研究可为低温环境下不同类型锂离子电池SOC的准确检测提供研究思路与数据参考。

1 超声检测锂离子电池荷电状态原理

超声波具有穿透性强、指向性好、便于检测和接收等优点，被广泛运用于工业无损检测领域。

超声波透射检测技术将两个超声换能器分别放置在被检试件的两个相对面。一个超声换能器用于发射超声波，另一个用于接收穿透试件后的超声信号，根据接收信号特征参数来评估被检试件状况。超声波透射检测技术方法如图1所示。

图1 超声波透射检测技术

超声波透射检测技术的机理为：超声波遇到由声阻抗不同的介质构成的界面时，将会发生反射与透射现象[24]。声阻抗为

锂离子电池充放电的本质是锂离子Li+在正极与负极材料之间不断地入嵌与脱嵌。充电时，Li＋从正极材料的空隙中脱出，经电解质传输，穿过隔膜，扩散至负极，并嵌入负极材料的层间，电子通过外电路到达负极，以此保持负极的电平衡；放电时则相反。在Li+入嵌与脱嵌的过程中，正负极材料的微观结构和介质的物理参数也在不断地发生变化。

超声信号对其穿透过的介质物理参数变化十分敏感，主要表现为其关键特征量超声飞行时间和信号幅值会出现明显变化。在不同的荷电状态下，电池内部材料的微观结构将发生变化，导致电池材料的声阻抗与弹性模量和密度变化，进而导致超声信号在其内部传播时发生衰减，传播速度发生变化。超声波在介质中的传播速度[22]为

式中，为介质的弹性模量，Pa。

因此，超声波透射检测技术可以依据超声飞行时间TOF和超声信号幅值SA检测锂离子电池的荷电状态。其中TOF主要由超声波在介质中的传播速度决定，SA主要由超声波在介质中的衰减决定。

2 低温锂离子电池试验研究平台

2.1 测试样品

本研究以松下公司生产的NCR18650B锂离子电池作为研究对象。该锂离子电池正极材料为镍钴铝三元材料，负极材料为石墨，标称电压为3.6V，标称容量为3.25A·h，放电截止电压为2.5V，充电截止电压为4.2V，放电温度范围为-20～60℃，充电温度范围为0～40℃，锂离子电池结构如图2所示。

图2 锂离子电池结构

2.2 测试方法

在低温环境下，基于超声透射技术对圆柱卷绕型锂离子电池荷电状态检测开展试验研究。使用美国物理声学公司谐振频率为150kHz的R15a超声换能器作为超声波的发射与接收装置。根据锂离子电池标准放电温度范围，本次试验检测环境温度设置为-20～10℃，温度梯度为5℃，温度波动范围为±0.5℃。利用单体电池测试仪对测试样品进行0.5恒流放电试验，容量每降低各检测环境温度下的最大可用容量的10%时进行一组超声波透射检测试验。锂离子电池SOC检测平台如图3所示。

图3 超声检测试验平台

图3中，信号发生器发出重复频率为50Hz、幅值为2V、脉宽为3.78μs的矩形脉冲激励信号，经过电压放大器放大后，幅值达到100V；示波器采样频率设置为12.5MHz。放大后的电压信号激励R15a超声换能器发出超声波。采用在耦合剂中添加一定量的无水乙醇来避免耦合剂在低温环境下出现凝固问题。超声换能器采用如图4所示的固定装置固定。该固定装置可以消除超声换能器两端受力不均匀的问题，保证接收端信号的稳定性，排除人为误差对检测结果造成的影响。放电检测开始前，将电池放置于试验箱内，在目标温度下静置2h，以保证电池内外部温度一致。

图4 超声换能器固定装置

2.3 数据处理方法

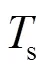
图5 同步触发信号与检测信号

图6 互相关算法求解流程

3 试验结果与量化关系研究

3.1 最大可用容量与温度量化关系

随着检测温度的降低，锂离子在电池内部的迁移受阻，导致可脱嵌的锂离子量减少，造成锂离子电池能够放出的最大可用容量不断降低。因此需要通过研究，掌握最大可用容量与温度的关系。

基于相关文献[26-28]，可脱嵌的锂离子量() （mol）可表示为

最大可用容量()（A·h）等于可用电荷量除以3 600s。由于可用电荷量等于基本电荷、阿伏伽德罗常数和可脱嵌的锂离子量三者的乘积，因此，不同温度下的最大可用容量()为

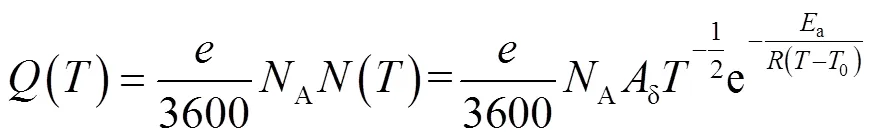
对式（6）两端同时取对数，得到

因此，可以建立不同检测温度下锂离子电池的最大可用容量与温度的量化关系，即

式中，、为对应项系数。

本研究中使用单体电池测试仪以0.5恒流放电至截止电压（2.5V）。静置1h后，再次恒流恒压充至满电，重复3次试验，以此确定锂离子电池在目标温度下的最大可用容量。低温环境下锂离子电池实际检测参数见表1。

表1 各温度下锂离子电池检测参数

Tab.1 Lithium-ion battery testing parameters at various temperatures

通过拟合不同检测温度下锂离子电池最大可用容量，建立了ln-关系曲线，如图7所示，拟合方程为

图7 不同环境温度下锂离子电池容量变化对数曲线

Fig.7 Logarithmic curve of lithium-ion battery capacity change under different ambient temperatures

图7中拟合曲线决定系数为0.990 6，方均根误差为0.063 8。这表明建立的关于锂离子电池的最大可用容量与温度的模型可以很好地逼近-20～10℃范围内的ln-关系式，且具有较高的精度。

3.2 超声信号特征选取

为实现基于超声信号特征的锂离子电池荷电状态检测，需要首先选取可准确反映荷电状态的超声信号特征。

分别在环境温度为-20℃、-15℃、-10℃、-5℃、0℃、5℃和10℃下以0.5放电倍率对锂离子电池进行放电试验，当容量每降低最大可用容量的10%时，进行一组超声波透射试验，每组试验采集5次超声透射信号波形；计算出透射信号幅值，并将透射信号与基准信号做互相关运算，求出信号之间的时延，依据式（3）求出各容量状态下对应的实际超声飞行时间；对每个容量步长下对应的5组数据取平均值以避免试验结果出现偶然性。得到不同检测温度下超声透射信号幅值和超声飞行时间与锂离子电池荷电状态之间的拟合曲线，分别如图8和图9所示，其拟合曲线决定系数见表2。

图8 不同温度下超声透射信号幅值与荷电状态之间的拟合关系

图9 不同温度下超声飞行时间与荷电状态之间的拟合关系

表2 不同温度下SA和TOF与锂离子电池SOC之间的拟合曲线决定系数

Tab.2 Coefficient of determination of fitting curve between SA and TOF and lithium-ion battery SOC at different temperatures

从表2中可以看出，低温环境下，相比超声信号幅值特征量，超声飞行时间特征量与SOC之间的线性关系更好。这是由于在低温环境下，锂离子电池材料对超声波的粘滞衰减较大，导致超声波波形畸变，进而降低了超声信号幅值读取的准确度，造成无法用超声信号幅值准确表征锂离子电池的荷电状态。而由于超声飞行时间是通过互相关算法求取，受信号波形畸变的影响较小，因此在低温环境下可以用超声飞行时间表征锂离子电池的荷电状态。

3.3 超声飞行时间与温度及荷电状态量化关系

超声飞行时间TOF与锂离子电池SOC的关系受环境温度影响（如图9所示），为使建立的超声飞行时间模型更加准确，应该同时考虑SOC和环境温度对TOF的影响，即TOF=(SOC,)。

超声飞行时间由信号在电池正极、隔膜和负极中的传播时间之和决定，由于温度和荷电状态的变化对超声信号在正极与隔膜中的传播时间影响较小[30-32]，超声飞行时间主要由超声信号在负极材料中的传播距离和传播速度所决定，即

式中，为信号在负极材料中的传播距离，即为负极材料的长度（m）；为负极材料弹性模量（Pa）；为负极材料质量（g）；为负极材料体积（m3），且等于假定不变的横截面积与负极材料长度的乘积；为超声信号在正极与隔膜中的传播时间（μs）。从式（10）可知，TOF主要受负极材料的弹性模量、质量和长度的影响。

首先分析负极材料弹性模量对TOF的影响，基于文献[33]，不同锂含量下负极材料的弹性模量E与可脱嵌的锂离子量有关，即

式中，为负极材料中锂离子含量；为负极材料中锂的弹性模量（Pa）；为负极材料中碳的弹性模量（Pa）；Li为负极材料中锂离子量（mol）；C为负极材料中碳原子量（mol）。

负极材料中锂离子量Li为锂离子电池在SOC=1时的负极材料中的锂离子量减去放电过程中从负极材料中脱嵌的锂离子量，即

参考文献[34]，不同锂含量的负极材料弹性模量与温度的关系为

式中，0为绝对零度下负极材料弹性模量（Pa）；为弹性模量温度系数。

综上分析，在不同检测温度下，锂离子电池放电过程中，负极材料弹性模量为

接下来分析负极材料质量对TOF的影响。放电过程中负极材料的质量变化主要由负极材料中脱嵌的锂离子质量所决定，即

由式（6）和式（9）可知，可脱嵌的锂离子量()为

则放电过程中可脱嵌的锂离子质量为

然后分析负极材料长度对TOF的影响。根据相关文献，传播距离在低温下的增长符合相似的阿伦尼乌斯方程[35]，即

综合上述分析，TOF=(SOC,)拟合关系设置如式（20）所示，拟合结果如图10所示。

式中，本模型中横截面积S假定不变，为0.003 3m2。

图10中拟合曲面的决定系数为0.966 8。拟合方程为

为了进一步评估拟合曲面与试验值的相对误差，以超声飞行时间的方均根误差（Root Mean Squared Error, RMSE）为指标，即

超声飞行时间曲面拟合的方均根误差为0.624 4μs，这表明建立的TOF=(SOC,)模型可以很好地逼近-20～10℃范围内实际的TOF-SOC关系式，且具有较高的精度。

为验证本文所建立的模型与关键参数的准确性，开展了10组不同环境温度、不同SOC值的检测试验，检测结果见表3。

表3 SOC估计试验结果

Tab.3 Results of SOC experiments

（续）

对表3中数据进行分析，绝对误差绝对值的平均值为2.23%。测试结果证明了本文所建立的模型与参数的准确性。

4 结论

本文研究证实了低温环境下超声透射技术检测圆柱卷绕型锂离子电池荷电状态的可行性。研究结果表明，在低温环境下，相较于超声信号幅值特征量，超声飞行时间特征量能更准确地表征锂离子电池的荷电状态。考虑低温对锂离子电池负极材料弹性模量、质量、长度的影响，建立了超声透射飞行时间与锂离子电池荷电状态及温度三者之间的量化方程，确定了其中的关键参数。结果表明，所提出的方程与试验数据的拟合决定系数为0.966 8，方均根误差为0.624 4μs。并开展了10组不同环境温度、不同SOC值的检测试验，SOC绝对误差绝对值的平均值为2.23%。试验结果表明在低温环境下，可以运用超声透射技术检测圆柱卷绕型锂离子电池的荷电状态。本研究可为低温环境下不同类型锂离子电池荷电状态的准确检测提供研究思路与数据参考。

[1] 黄云辉. 锂离子电池: 20世纪最重要的发明之一[J]. 科学通报, 2019, 64(36): 3811-3816.

Huang Yunhui. Lithium-ion battery: one of the most important inventions in the 20th century[J]. Chinese Science Bulletin, 2019, 64(36): 3811-3816.

[2] Duan Jian, Tang Xuan, Dai Haifeng, et al. Building safe lithium-ion batteries for electric vehicles: a review[J]. Electrochemical Energy Reviews, 2020, 3(1): 1-42.

[3] Alipour M, Ziebert C, Conte F V, et al. A review on temperature-dependent electrochemical properties, aging, and performance of lithium-ion cells[J]. Batteries, 2020, 6(3): 35.

[4] Luo Maji, Guo Yazhou, Kang Jianqiang, et al. Ternary-material lithium-ion battery SOC estimation under various ambient temperature[J]. Ionics, 2018, 24(7): 1907-1917.

[5] Lin H P, Chua D, Salomon M, et al. Low-temperature behavior of Li-ion cells[J]. Electrochemical and Solid-State Letters, 2001, 4(6): A71-A73.

[6] Berecibar M, Gandiaga I, Villarreal I, et al. Critical review of state of health estimation methods of Li-ion batteries for real applications[J]. Renewable and Sustainable Energy Reviews, 2016, 56: 572-587.

[7] 杨若岑, 冬雷, 廖晓钟, 等. 电池剩余容量估算方法综述[J]. 电气技术, 2019, 20(10): 1-5, 57.

Yang Ruocen, Dong Lei, Liao Xiaozhong, et al. A review on battery remaining capacity estimation[J]. Electrical Engineering, 2019, 20(10): 1-5, 57.

[8] Rodrigues M T F, Babu G, Gullapalli H, et al. A materials perspective on Li-ion batteries at extreme temperatures[J]. Nature Energy, 2017, 2(8): 17108.

[9] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.

Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.

[10] 许守平, 胡娟, 侯朝勇. 储能用锂离子电池动态阻抗模型及其特征参数研究[J]. 电气技术, 2018, 19(8): 90-94.

Xu Shouping, Hu Juan, Hou Chaoyong. Study on the dynamic impedance model and characteristic parameters of lithium ion battery for energy storage system[J]. Electrical Engineering, 2018, 19(8): 90-94.

[11] 程俊, 曲妍, 李媛, 等. 基于剩余电量估计的电池组充放电均衡策略[J]. 电力系统保护与控制, 2020, 48(3): 122-129.

Cheng Jun, Qu Yan, Li Yuan, et al. Charge and discharge equalization strategy for battery packs based on remaining capacity estimation[J]. Power System Protection and Control, 2020, 48(3): 122-129.

[12] 焦自权, 范兴明, 张鑫, 等. 基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3993.

Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3993.

[13] 申彩英, 左凯. 基于开路电压法的磷酸铁锂电池SOC估算研究[J]. 电源技术, 2019, 43(11): 1789-1791.

Shen Caiying, Zuo Kai. Research on SOC estimation of LiFePO4batteries based on open circuit voltage method[J]. Chinese Journal of Power Sources, 2019, 43(11): 1789-1791.

[14] 杨文荣, 朱赛飞, 陈阳, 等. 基于改进安时积分法估计锂离子电池组SOC[J]. 电源技术, 2018, 42(2): 183-184, 246.

Yang Wenrong, Zhu Saifei, Chen Yang, et al. SOC estimation of lithium-ion battery based on improved ampere-hour integral method[J]. Chinese Journal of Power Sources, 2018, 42(2): 183-184, 246.

[15] 梁培维, 张彦会. 基于欧姆内阻对锂电池健康状态的估算[J]. 电源技术, 2019, 43(10): 1623-1625, 1704.

Liang Peiwei, Zhang Yanhui. Estimation of lithium battery health based on ohmic internal resistance[J]. Chinese Journal of Power Sources, 2019, 43(10): 1623-1625, 1704.

[16] 宫明辉, 乌江, 焦朝勇. 基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J]. 电工技术学报, 2020, 35(18): 3972-3978.

Gong Minghui, Wu Jiang, Jiao Chaoyong. SOC estimation method of lithium battery based on fuzzy adaptive extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3972-3978.

[17] 邓哲, 黄震宇, 刘磊, 等. 超声技术在锂离子电池表征中的应用[J]. 储能科学与技术, 2019, 8(6): 1033-1039.

Deng Zhe, Huang Zhenyu, Liu Lei, et al. Applications of ultrasound technique in characterization of lithium-ion batteries[J]. Energy Storage Science and Technology, 2019, 8(6): 1033-1039.

[18] 马广廷. 超声波用于锂离子电池SOC的预测及内部气体检测的探究[D]. 武汉: 华中科技大学, 2019.

[19] Deng Zhe, Huang Zhenyu, Shen Yue, et al. Ultrasonic scanning to observe wetting and “unwetting” in Li-ion pouch cells[J]. Joule, 2020, 4(9): 2017-2029.

[20] Sood B, Osterman M, Pecht M. Health monitoring of lithium-ion batteries[C]//2013 IEEE Symposium on Product Compliance Engineering (ISPCE), Austin, TX, USA, 2013: 1-6.

[21] Gold L, Bach T, Virsik W, et al. Probing lithium-ion batteries' state-of-charge using ultrasonic transmission-concept and laboratory testing[J]. Journal of Power Sources, 2017, 343: 536-544.

[22] Hsieh A G, Bhadra S, Hertzberg B J, et al. Electrochemical-acoustic time of flight: in operando correlation of physical dynamics with battery charge and health[J]. Energy & Environmental Science, 2015, 8(5): 1569-1577.

[23] Davies G, Knehr K W, van Tassell B, et al. State of charge and state of health estimation using electrochemical acoustic time of flight analysis[J]. Journal of the Electrochemical Society, 2017, 164(12): A2746-A2755.

[24] Robinson J B, Maier M, Alster G, et al. Spatially resolved ultrasound diagnostics of Li-ion battery electrodes[J]. Physical Chemistry Chemical Physics, 2019, 21(12): 6354-6361.

[25] 李均浩, 刘文红. 一种改进的非整数自适应时延估计方法[J]. 应用声学, 2019, 38(2): 253-260.

Li Junhao, Liu Wenhong. An improved fractional adaptive time delay estimation method[J]. Journal of Applied Acoustics, 2019, 38(2): 253-260.

[26] 任元, 邹喆乂, 赵倩, 等. 浅析电解质中离子输运的微观物理图像[J]. 物理学报, 2020, 69(22): 46-62.

Ren Yuan, Zou Zheyi, Zhao Qian, et al. Brief overview of microscopic physical image of ion transport in electrolytes[J]. Acta Physica Sinica, 2020, 69(22): 46-62.

[27] Chung S H, Such K, Wieczorek W, et al. An analysis of ionic conductivity in polymer electrolytes[J]. Journal of Polymer Science Part B: Polymer Physics, 1994, 32(16): 2733-2741.

[28] Albinsson I, Mellander B E, Stevens J R. Ionic conductivity in poly(propylene glycol) complexed with lithium and sodium triflate[J]. The Journal of Chemical Physics, 1992, 96(1): 681-690.

[29] Xu Li, Cui Xianbao, Zhang Ying, et al. Measurement and correlation of electrical conductivity of ionic liquid [EMIM][DCA] in propylene carbonate and γ-butyrolactone[J]. Electrochimica Acta, 2015, 174: 900-907.

[30] Jaguemont J, Boulon L, Dubé Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures[J]. Applied Energy, 2016, 164: 99-114.

[31] Davies G. Characterization of batteries using ultrasound: applications for battery management and structural determination[D]. Princeton: Princeton University, 2018.

[32] Zhang S S, Xu K, Jow T R. Low temperature performance of graphite electrode in Li-ion cells[J]. Electrochimica Acta, 2002, 48(3): 241-246.

[33] Lee J H, Kim C. Effective modulus of Si electrodes considering Li concentration, volume expansion, pore, and Poisson's ratio of Li-ion batteries[J]. Journal of Mechanical Science and Technology, 2021, 35(5): 2115-2121.

[34] Hu Bin, Zhu Yuhong, Shi Chao. Effect of temperature on solid ultrasonic propagation using finite element method and experiments[C]//2018 IEEE Far East NDT New Technology & Application Forum (FENDT), Xiamen, China, 2018: 107-111.

[35] 王祥, 康健强, 谭祖宪. 基于电化学衰退模型研究锂离子电池SEI反应[J]. 化学工程与技术, 2018, 8(2): 137-150.

Wang Xiang, Kang Jianqiang, Tan Zuxian. Study on SEI reaction of lithium-ion batteries based on the electrochemical degradation model[J]. Hans Journal of Chemical Engineering and Technology, 2018, 8(2): 137-150.

Relationship between State of Charge of Lithium-Ion Battery and Ultrasonic Transmission Flight Time at Low Temperature

Wu Lifeng Liu Hao Lin Zhongqin Xu Ce Ma Guoming

（State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China）

To obtain the relationship between state of charge of lithium-ion battery and ultrasonic transmission features at low temperature, experiments and theory analysis on ultrasonic detection of the state of charge of cylindrically wound lithium-ion batteries were carried out. A fixing device was developed to improve the sensing stability and sensitivity. The feature extraction algorithm was proposed to extract ultrasonic signal amplitude (SA) and ultrasonic time-of-flight (TOF). The research on SOC detection by ultrasonic transmission method at low temperature was carried out. The maximum usable capacity of lithium-ion batteries was obtained. The results show that, the TOF is more accurate than the SA in state of charge detection of the lithium-ion battery at low temperature. The effects of low temperature on the elastic modulus, quality, and length of lithium-ion battery anode materials were investigated, and the quantified equations for the state of charge and ultrasonic transmission flight time of lithium-ion battery at low temperature were established. The coefficient of determination of the fitting between the quantization equation and the test data is 0.9668. This study can provide a reference for the accurate detection of lithium-ion battery SOC at low temperature.

Low temperature, lithium-ion battery, state of charge, ultrasound transmission method, ultrasonic signal amplitude, ultrasonic time of flight

10.19595/j.cnki.1000-6753.tces.211237

TM912

国家自然科学基金（51977075）、北京市自然科学基金（3182036）、中国科协青年人才托举工程（YESS20160004）、中央高校基本科研业务费（2019MS006）和新能源电力系统国家重点实验室（华北电力大学）自主研究课题（LAPS2020-08）资助项目。

2021-08-09

2021-11-10

吴立峰 男，1997年生，硕士研究生，研究方向为锂离子电池荷电状态检测。E-mail：120192201492@ncepu.edu.cn

马国明 男，1984年生，教授，博士生导师，研究方向为电气设备在线监测与故障诊断、高电压与绝缘技术。E-mail：ncepumgm@163.com（通信作者）

（编辑 李冰）