求解随机向量变分不等式的样本平均逼近方法

黄章乙*，赵玉昌

（重庆交通大学数学与统计学院，重庆 400074）

引言

随机向量变分不等式（SVVI）问题：即求解x*∈S，使得

由于(1)中包含了随机向量，受到Gürkan[1]提出的期望值(EV)模型的启发，用期望值(EV)方法来处理式(1)，得到下述随机向量变分不等式问题的期望值模型

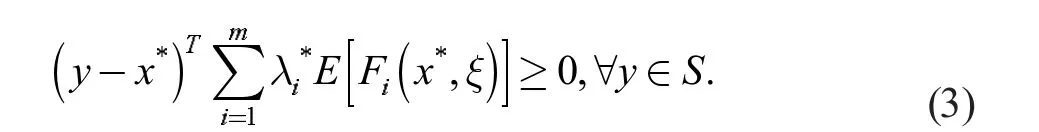
为了求解问题(3)的解，受Fukushima[4]研究变分不等式提出的间隙函数启发，定义如下正则化间隙函数g:Rn×Λ→[0，∞]

1 解的存在性

在本节中，我们给出了正则化间隙函数g（x，λ）在集合S×Λ 上强制性成立的充分条件。因此，对于足够小的α＞0 问题(6)总有一个最优解。

证明. 参考文献[3]中定理1 的证明方法，可以得到定理2.1 的结论，定理得证。

2 近似问题的收敛性分析

引理3.1[5]假设①-③成立，则以下结论成立：

(1) 函数f（x，λ）在集合S×Λ 上连续；

(2) 函数列{fN（x，λ）}在集合S×Λ 上依概率1一致收敛于f（x，λ），则有

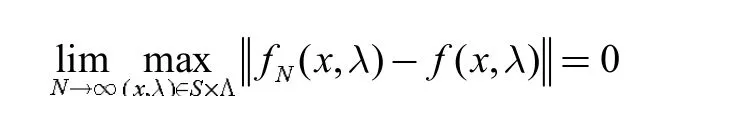
下面，我们讨论目标函数逼近问题(7)的一致收敛性。

定理3.1 假设①-③成立，函数列{gN（x，λ）}在集合S×Λ 上依概率1 一致收敛到函数g（x，λ）。

证明. 由gN（x，λ）和g（x，λ）的定义有

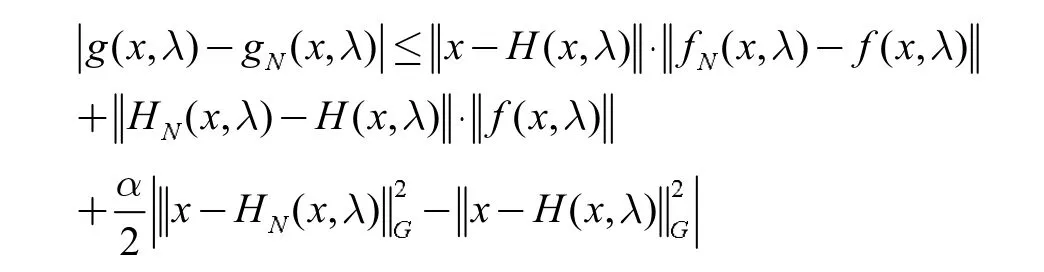
因此，可得

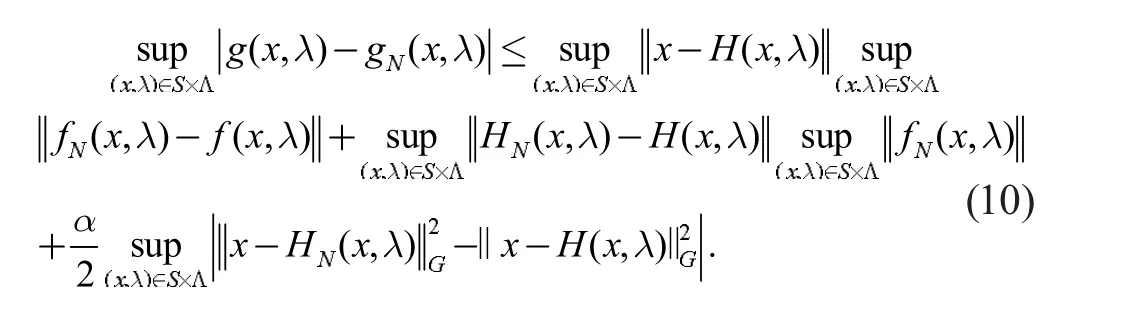
因为g（x，λ）≥0，故

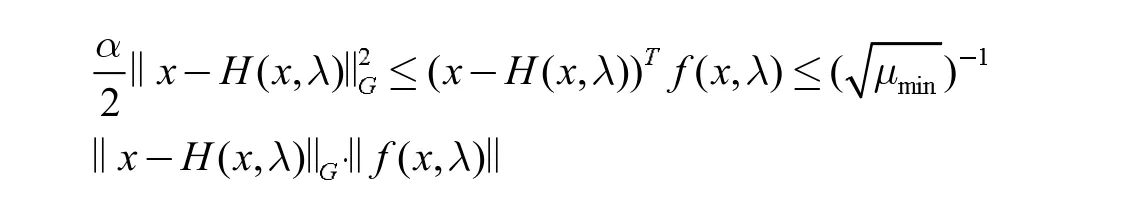
其中μmin表示矩阵G 的最小特征值，由上式进一步可得到

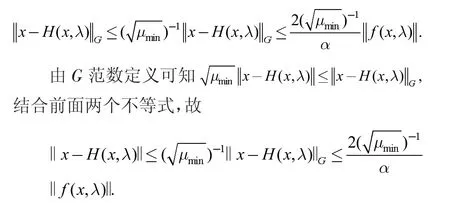
由于集合S×Λ 为非空紧的，故存在一个常数M＞0，使得，

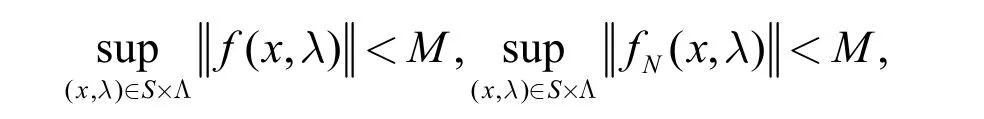
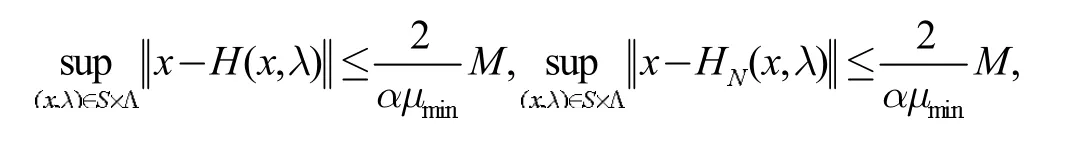
依概率1 成立。不难得到依概率1 成立。另外，根据函数H（x，λ）和HN（x，λ）的定义及投影的非扩张性质，可知

依概率1 成立。同理采用和上式同样放缩法有

这表明函数列fN依概率1 上图收敛于函数f。此外，由于H（x，λ）和HN（x，λ）都是连续函数及投影的非扩张性，故

采用与定理3.3 类似方法，可知

依概率1 成立。由上述两个不等式可得

依概率1 成立。因为（x*，λ*）∈S×Λ，这表明着（x*，λ*）∈S*依概率1 成立，定理得证。

3 结论

本文首先借助标量化方法以及正则化间隙函数将随机向量变分不等式问题转化为随机优化问题求解。然后在适当条件下讨论了所得随机优化问题解的存在性。最后，利用样本平均逼近方法处理得到的随机优化问题中的数学期望，讨论了近似问题最优值及最优解集的收敛性。所得结果为随机向量变分不等式问题的求解提供了一种新方法。