间歇循环荷载下粉土路基动力特性及累积变形研究

2022-11-12吴遥杰周浩东宫全美

华东交通大学学报 2022年4期

吴遥杰，周浩东，宫全美

（1. 同济大学道路与交通工程教育部重点实验室，上海 201804; 2. 中南大学土木学院，湖南长沙 410083）

动三轴试验是研究路基土动力变形的有效手段，国内外学者对不同路基土累积塑性应变随动荷载循环振次的变化规律进行了大量研究[1-3]。Puppala等[4]通过对黏土、粉土、砂土进行动三轴试验，提出了以应力状态和荷载循环次数为函数的路基土永久变形预测模型；Duong 等[5]通过对由路基土和道砟“混合层”进行大型动三轴试验，研究了不同应力水平及含水率下细颗粒含量对“混合层”永久变形的影响；Salour 和Tang 等[6-7]采用多阶段循环三轴试验研究了含水率、动应力幅值、围压等对路基土产生的累积变形的影响，提出了考虑应力历史的永久变形预测模型；蔡英等[8]通过动三轴试验研究了路基土体的永久变形和临界动应力受加载次数、频率及围压影响规律；周文权、冷伍明、梅慧浩等[9-11]对粗粒土填料开展动三轴试验，研究了不同围压、含水率、动应力幅值对循环荷载下粗粒土填料动强度及变形特性的影响规律，并提出了粗粒土填料累积变形稳定界限状态判别准则；董城等[12]通过动三轴试验对粉土路基在不同压实度、动应力及含水率下的累积塑性应变的变化规律进行研究，获得了粉土路基的临界动应力随含水率的变化规律，建立了粉土路基累积塑性变形预测模型。

而上述研究大多考虑连续循环加载，忽略了列车荷载的间歇效应，不能反映铁路列车荷载的实际情况。目前循环动三轴试验中考虑间歇效应的研究不多，且主要针对软黏土。Yildirim[13]设计加载-间歇动三轴试验，分析了软黏土的孔压、应变随振次、及加载阶段的变化规律；王军、丁建宇等[14-15]对饱和软黏土开展分阶段循环动三轴试验，发现间歇加载下不排水试样停振期孔压基本不变、变形部分恢复，且循环振次越大，恢复比例越高，排水条件下试样在间歇期产生的累积应变随阶段数增加而减少；何绍衡等[16]通过对饱和原状海相软土进行不排水加载-间歇循环三轴试验，研究在间歇循环荷载作用下的土体变形及孔压变化规律，并将其与连续振动试验对比，分析间歇效应对土体长期力学性能的影响。

我国早期重载铁路建设标准低，粉土路基被广泛运用于我国黄淮海平原地区的几条主要铁路干线（如朔黄铁路），使路基在列车动荷载和基床土质湿度增加共同作用下极易形成病害，在货运重载化趋势下更为严重[17]，鉴于此，考虑不同动应力幅值、含水率、加载振次、间歇效应及排水条件，进行了一系列动三轴试验，研究重载铁路粉性路基土在列车间歇荷载作用下动力特性和累积变形，为重载铁路粉土路基动稳定性评价，合理选择列车间歇时间提供理论参考。

1 试验方案

1.1 土样制取

试验用土为朔黄铁路西柏坡段（K248）路基细粒土填料，通过一系列土工试验确定土样为低液限粉土（ML），填料组别属于C3。土体的土粒比重Gs，最大干密度ρdmax，最优含水率ωopt，饱和含水率ωsat，液限ωl，塑限ωp，塑性指Ip10和渗透系数k20见表1。级配曲线如图1，d 为土体粒径，Cu为土粒的不均匀系数，CC为曲率系数。试验仪器为DDS-70 微机控制动三轴仪。试样采用击实法制取，按压实度K=0.95，分5 层击实，试样直径为39.1 mm，高80 mm。饱和试样采用抽气真空饱和，具体试验步骤严格按照《铁路工程土工试验规程》（TB 10102—2010）执行。

图1 颗粒级配曲线Fig. 1 Gradation curve for the tested silty soil

表1 土样的基本物理指标Tab.1 Basic physical property parameters of soil sample

1.2 试验条件

结合朔黄铁路实际情况，选取3 组围压σ3=30，60，90 kPa 模拟埋深0～6 m 铁路路基填料实际所受侧压环境。本试验选取最优含水率（11.80%），大于最优含水率（15%，17.5%）和饱和含水率（19.75%）4 组含水率，对应的饱和度分别为0.6，0.76，0.89 和1。根据梅慧浩等[18]通过建立列车-轨道-路基三维动力有限元模型，计算得轴重25～30 t的列车对路基面产生的动应力峰值最大值位于91～123 kPa 之间。考虑到路基随着深度增加动应力的衰减情况，本次试验取动应力幅值σd=30，60，90，120，150，180 kPa。路基所受列车通过荷载的频率f=v/l，其中v 为列车运行速度，l 为车厢长度。根据现场调研，重载列车v 为60～80 km/h，以C80 货车为例，火车车厢长度l 为12 m，则f 为1.39～1.85 Hz，本次试验取f 为2 Hz。

1.3 试验方案

试验采用应力控制加载，荷载形式为偏压正弦波。采用排水等压固结（即固结压力为围压）。试验开始前先加静偏应力σs=（15+σd） kPa，模拟轨道和道砟的静力作用，然后加正弦动应力模拟列车荷载。试验终止条件采用应变标准和振动次数双重控制，对于发生破坏的试样采用轴向应变达到10%时作为破坏标准（即试验终止条件），对于不发生破坏的试样，每一阶段以振动次数达到2 000 次为试验停止条件（研究加载振次影响时按具体情况选取），共5 个阶段，即最大振次为10 000 次。加载方式选取连续加载和分阶段间歇加载（改变加载振次NL和间歇时长TP），如图2。对于改变间歇时长和加载方案的试验，试验方案如表2。

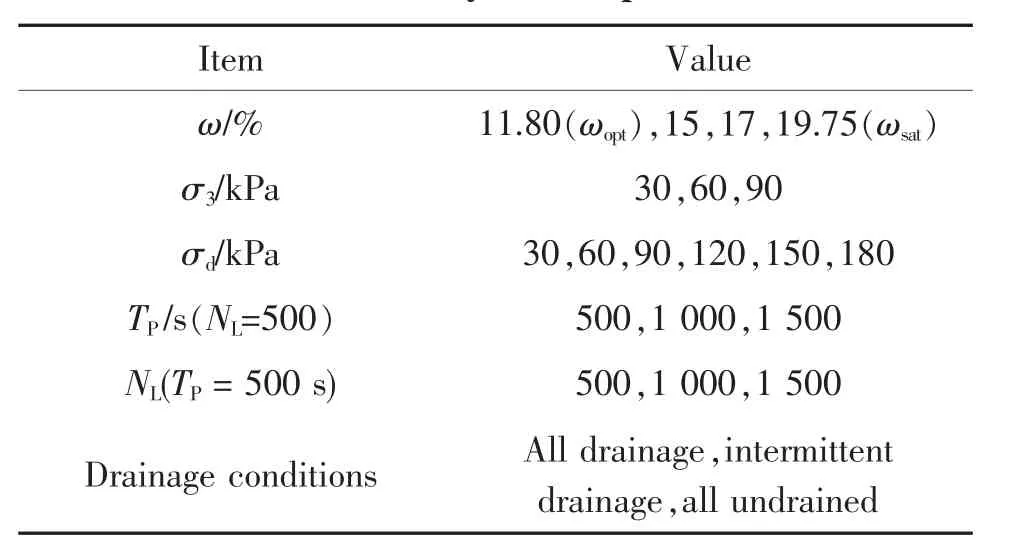
表2 试验方案Tab.2 Summary of tests performed

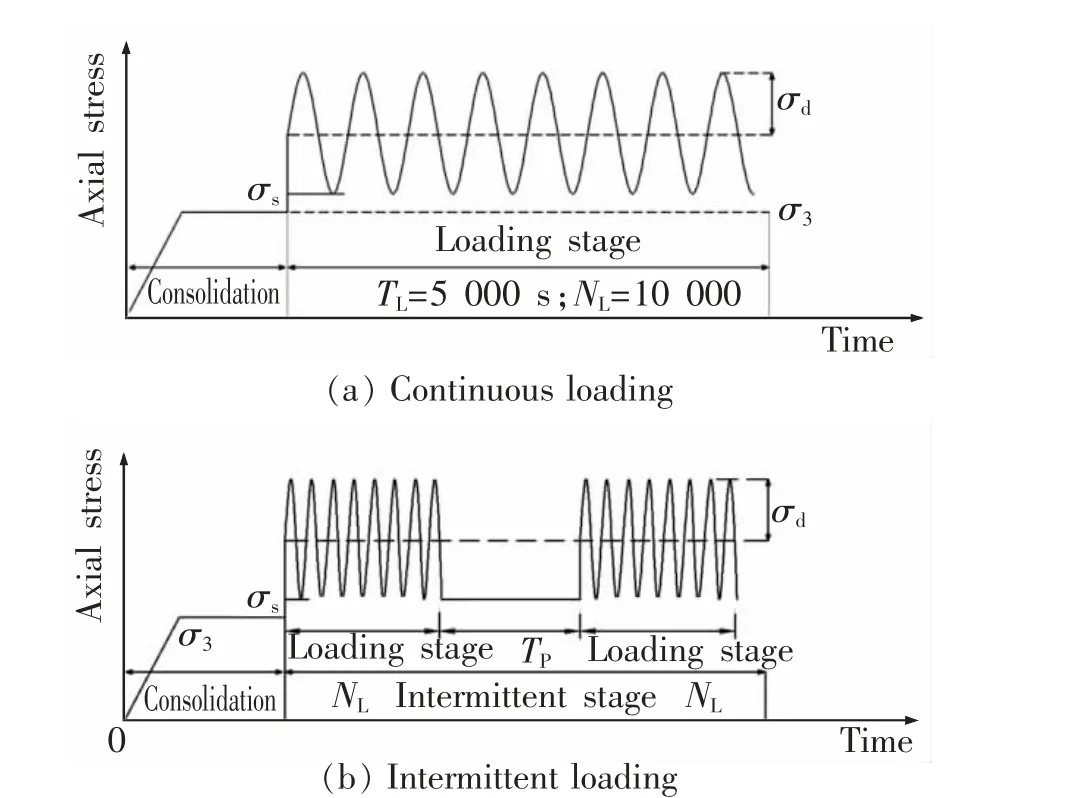
图2 不同加载方式示意图Fig.2 Schematic diagram of different loading moeds

2 动力特性分析

2.1 粉土临界动应力

20 世纪60 年代起，国内外学者开始研究循环荷载下路基土临界动应力的确定问题[19]。蔡英等[8]根据不同动应力下试样累积应变随振次变化曲线特点分为衰减型（后来许多学者也称稳定型）和破坏型。本文参考上述学者对累积变形曲线的划分，定义介于衰减型和破坏型之间的曲线为临界型，其对应动应力为该条件下临界动应力σdcr。

图3 为σ3=30 kPa 时不同含水率试样累积应变随振次关系曲线。图3（a）、图3（b）中蓝色曲线为临界型，对应可知σ3=30 kPa，ω=11.80%，15%的试样临界动应力分别为σdcr=120，90 kPa。土的临界动应力由本身物理性质和所处应力环境决定。理论上围压σ3和含水率ω 一定时为定值，但由于制样差异、试样数量有限，有些条件下无法确定临界动应力具体数值，仅能确定一个范围，如图3（c）饱和试样在σ3=30 kPa 时临界动应力应介于30～45 kPa 之间。

图3 不同动应力下εp～N 关系曲线Fig.3 εp～N relation curve under different dynamic stress

周文权等[10]曾通过类似的“逼近法”确定试样临界动应力，但该方法对试样质量及数量要求较高，下文给出一种确定临界动应力的新方法。

图4 为某一振次试样的累积应变εp与动应力幅值σd的关系曲线。由图4 可知，各种含水率和围压下试样累积应变随动应力均表现为“双线性”发展趋势：即当动应力幅值小于某一应力水平时，εp随σd缓慢增大；当动应力幅值大于该应力水平时，εp随σd迅速增大。在给定的试验条件下，对小于和大于该动应力水平的εp与σd的数据点进行拟合并延长，两条直线存在一个交点。如图4 中黑色圆点标记所示。根据该交点左右两侧试样累积塑性应变εp的增长规律，可将该点对应的动应力作为试样在某一特定含水率和围压下的临界动应力。从图中可看出，σ3=30 kPa，ω=11.80%，15%条件下，图中交点分别为120，110 kPa。与从图3 中得到的临界动应力σdcr=120，90 kPa 有一定的误差，但理论上从图3 并不能得到临界动应力的确定数值，而只能得到临界动应力的某一范围。而采用图4 中的“双线性”拟合求交点的方法，能够一定程度上剔除异常数据，如σ3=90 kPa，ω=19.75%情况，从而避免试验及人为误差的影响，且该方法确定的临界动应力值是一定值。

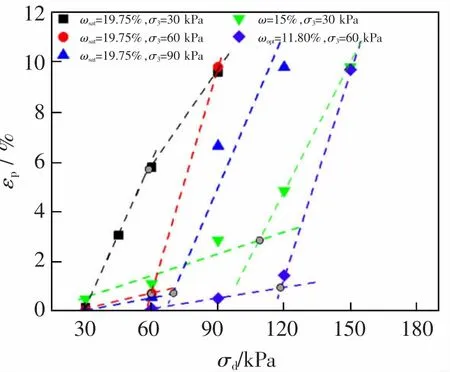
图4 εp～σd 关系曲线（N=2 000 次）Fig.4 εp～σd relation curve while N=2 000 times

需要注意的是采用该方法求临界动应力时，应确保在该循环振次下试样累积塑性应变已稳定，基于此尽量选择循环振次N 较少的情况，如图4取N=2 000 次，从而获得较多动应力幅值对应累积应变的数据，减少试验误差。此外在选取数据时，当有多个动应力幅值下试样破坏时均未达到选取的循环振次，只选取较小动应力幅值对应的数据，如图3（a）中由于N=2 000 次，故应选取的数据中最大动应力幅值为150 kPa，而不是180 kPa。

临界动应力由本身的物理性质决定，同时也受应力条件影响，为研究含水率及围压对临界动应力的影响，定义临界动应力比

式中：σdcr为临界动应力，μ 为对应临界动应力比。根据图4 临界动应力数据得到表3。

根据表3，以ω 为横坐标，μ 为纵坐标拟合得到图5。拟合直线方程为

图5 μ～ω 拟合曲线Fig.5 Fitting Curve of critical dynamic stress ratio μ with water content ω

表3 临界动应力试验值及推算值Tab.3 Test and estimated values of critical dynamic stress

从式（2）可知，低围压下（σ3<90 kPa）临界动应力比随含水率增加线性减小，当含水率一定时，临界动应力随围压线性增大。这与冷伍明等[10]关于粗粒土临界动应力得到的结论相似，也与蔡英[8]等对黏性土临界动应力的研究结论相符。可见，路基土的临界动应力随含水率增加显著下降，即路基土的含水状态应予以重视。

2.2 粉土临界含水率

为进一步研究含水率对土体累积塑性应变影响，并分析动应力幅值、围压和含水率的叠加效应，绘出N=2 000 次累积塑性应变与含水率的关系曲线图εp～ω 如图6。

由图6 可知，随含水率增大，各种试样累积塑性应变呈现类似动应力幅值影响的“双线性”发展趋势：当含水率低于某一值时，随着含水率的增加，εp～ω 关系曲线较为平缓，即累积塑性应变随含水率的增加增速较小；而当含水率大于某一值时，随着含水率的增加，εp～ω 关系曲线较陡，即累积塑性应变随含水率增加迅速增加。说明对于非饱和状态的路基土，存在一种“临界含水率”，当含水率高于“临界含水率”，路基土将处于一种不稳定状态，较小的应力条件的改变就会引起较大的累积变形，影响铁路行车安全。对于非饱和铁路路基土，尤其是对于渗透系数较低的粉土路基，应加强路基土排水，使路基土含水率处于“临界含水率”以下，而不仅是避免土体饱和。由于不同含水率试样数量有限，下面取3 种情况对于临界含水率的确定方法简单说明。

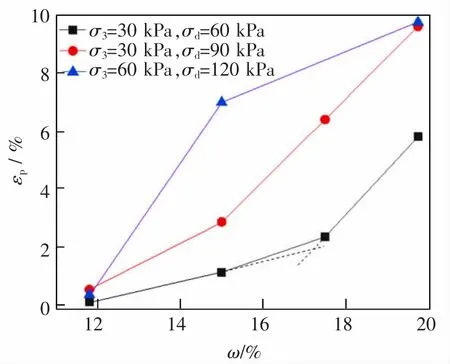
图6 εp～ω 关系曲线(N=2 000 次)Fig.6 εp～ω relation curve while N=2 000 times

对于σ3=30 kPa，σd=60 kPa 的情况，可知4 种含水率情况形成了3 段折线，且前两段折线斜率相近，说明临界含水率非常接近第3 种含水率（17.5%），为较准确地确定临界含水率的具体数值，将第1、第3 段线延长交于一点，该点对应的含水率（图6 中为ω2）即为该条件下的临界含水率。对于σ3= 30 kPa，σd=90 kPa，可知后3 种含水率所对应的点恰好处在同一直线上，这说明“双线性”法求临界含水率具有一定的可靠性，同时也说明第2 种含水率（ω1=15%）即为该条件下的临界含水率。对于σ3=60 kPa，σd=120 kPa 的情况，由于只有3 种含水率的数据，实际上无法为“双线性”法确定临界含水率提供支持，而只能作为一种参考，说明此条件下临界含水率也接近ω1=15%。

3 间歇效应对粉土累积变形的影响

对于路基上某一点，当列车通过时，可认为对其施加连续荷载，当该列车通过后，该点不受动荷载作用，直至下一列车到达该位置对其施加荷载，即列车对路基的荷载实际上是由一段连续荷载和一段停歇交替形成的周期性非连续荷载。

3.1 间歇存在对粉土累积变形的影响

图7 为最优含水率试样连续振动和间歇加载的εp～N 曲线。由图7 可知，相同条件下间歇加载和连续加载试样在N=0～2 000 次内的曲线接近重合。当N＞2 000 次后，相同条件下连续加载方式的试样累积塑性应变持续增长，振次未达到10 000 次时试样均已破坏，而间歇加载方式的试样最终都完成了总计10 000 次的加载。这说明间歇加载能明显减缓塑性应变的累积和发展。

图7 连续加载和间歇加载的εp～N 关系曲线Fig.7 εp～N relation curve under continuous loading and intermittent loading

3.2 间歇时长对粉土累积变形的影响

为进一步研究间歇效应对累积塑性应变的影响，考虑通过改变间歇时长TP研究试样εp随N 的变化规律。图8 的加载振次NL为500 次，TP分别为500，1 000 s 和1 500 s。为方便对比分析，通过适当平移将不同间歇时长对应图中加载振次均转化为2 000 次，从而使不同间歇时长对应试样各阶段加载开始和结束阶段对应的振次相同。

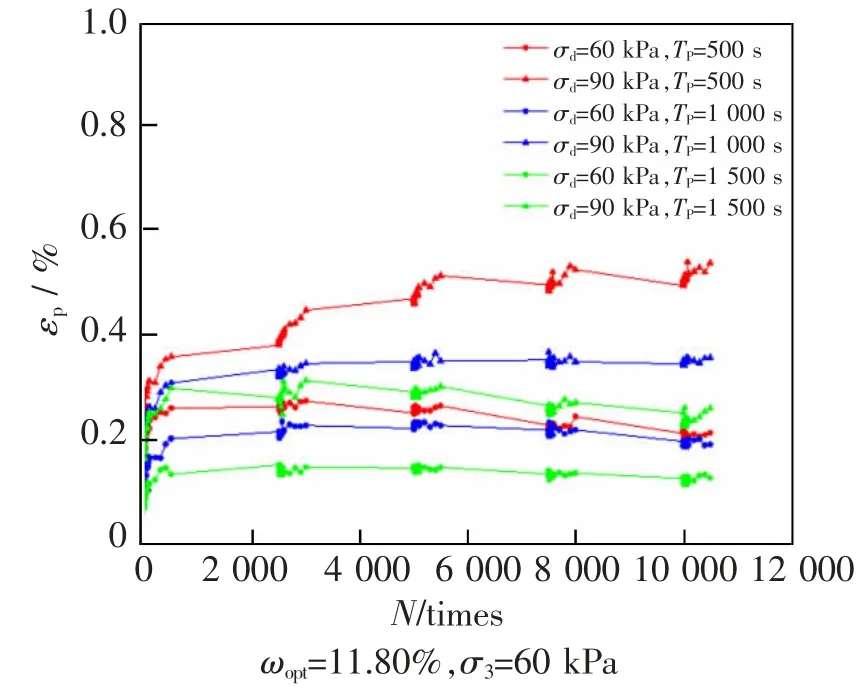
图8 改变间歇时长加载的εp-N 关系曲线Fig.8 εp-N relation curve loaded by changing intermittent duration

由图8 可知，不同间歇时长下应力状态相同的试样在N=0～500 次内的累积塑性应变随振次的发展规律基本相同，但在N＞500 次后，间歇时间的长短对试样的累积塑性应变的影响逐渐凸显，随着间歇阶段数的增加，间歇时长的不同造成累积塑性应变的差异越来越大。

对比两种动应力条件的试样，可知间歇时长越长，两者累积塑性应变发展的差异也越小，这说明当间歇时长达到一定程度，动应力幅值对累积塑性应变的影响较小，试样累积塑性应变会逐步稳定。

3.3 加载振次对粉土累积变形的影响

一般重载列车单次经过某点时产生的振动次数不到2 000 次，故考虑在控制间歇时间不变的条件下减少单阶段振动次数。图9 为改变加载振次下试样εp与N 的关系曲线。

由图9 可知，相同动应力幅值条件下，各种加载振次试样在N=0～500 次内累积塑性应变大致相似，在N＞500 次后随着循环振次的增加，先进入间歇的试样累积塑性应变停止增加，当在N＞1 000次后，加载1 500 次的试样累积塑性应变迅速增大，与提前进入间歇的试样差异逐渐增大。后几个加载阶段各种情况试样的累积塑性应变都逐渐稳定，最终呈现加载次数越大，累积塑性应变越大的情况。

图9 改变加载振次的εp～N 关系曲线（σ3=60 kPa）Fig.9 εp～N relation curve loaded by changing loading times (σ3=60 kPa)

图9 中出现了σd=90 kPa 时NL=500 次的试样的累积塑性应变大于NL=1 000 次，这可能是绘图方法导致。由于将不同加载振次的试样累积塑性应变随循环振次变化曲线绘制在同一张图中时，会出现同一循环振次下，加载振次较多的试样还在前一振动阶段而加载振次较少的试样已经进入下一个间歇的情况。前者累积塑性应变可能正在增加，而后者处于间歇阶段，累积塑性应变保持不变甚至减少。

3.4 间歇与加载相对系数对粉土累积变形的影响

上文分别研究了间歇时长和加载振次对累积塑性应变的影响，为研究两者影响的综合作用效应，引入间歇与加载相对系数λ 的概念。

式中：TL为单阶段加载振次NL对应的时长，由下式求出

式中： f 为加载频率， f=2 Hz。

图10 为在ωopt=11.8%，σ3=60 kPa 条件下σd=60 kPa 和σd=90 kPa 试样的最大累积塑性应变εpmax随λ 的变化曲线。由图10 可知，随着λ 的增大，εpmax减小，这表明间歇时长越长、加载振次越小，土体的动力响应越弱，循环荷载长期作用下其能达到的累积变形最大值越小。

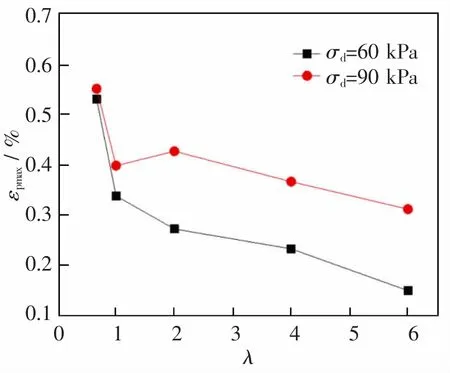
图10 εpmax～λ 的关系曲线Fig.10 The relation curve of the maximum accumulative plastic strain εpmax with the relative coefficient λ

综上分析，间歇的存在对路基土体长期累积变形的发展有显著影响。经过间歇阶段的卸载排水，土体内部结构不断调整并最终趋于稳定，试样抵抗后续累积变形的能力得到提高，在相同振次内的累积塑性应变相对较小。这说明，对于铁路路基土来说，列车荷载间歇时间越长，加载振次越少，越有利于土体动力稳定。

4 排水条件对粉土累积变形的影响

为研究排水条件对循环荷载作用下土体累积塑性应变的影响，在前文选取的加载不排水、间歇排水的基础上增设加载、间歇均排水和加载、间歇均不排水两种工况，图11 为饱和试样在不同排水条件下受到连续振动-停振1 000 s 荷载作用下εp与N 的关系曲线。

由图11 可知，在相同应力条件下，加载不排水，间歇排水和加载、间歇均不排水的试样在N=0～2 000 次内试样均处于不排水加载状态；因此两种排水条件在N=0～2 000 次内累积塑性应变发展趋势基本一致。相比而言，加载、间歇均排水试样则由于加载过程中持续能够排水，该阶段的累积塑性应变明显较小。

图11 不同排水条件下间歇加载εp～N 关系曲线Fig.11 εp～N relation curve intermittent loaded under different drainage conditions

在N＞2 000 次后，间歇阶段排水条件的不同会导致加载不排水，间歇排水和加载间歇均不排水两种排水条件下试样累积塑性应变的发展开始出现差异。间歇不排水条件下试样土体内部由于水分不能及时排出，循环荷载导致的超孔隙水压力逐步增大，造成有效应力减小，累积塑性应变快速增长直至试样的破坏。故在此排水条件下，对于稳定试样（动应力较小）累积塑性应变较大；对于破坏试样（动应力较大）往往较早发生破坏。而对于加载、间歇均排水试样：在较大动应力下虽然随振次的增加，累积塑性应变也逐步增大，但由于土体水分能及时排出，土体结构能逐步调整，最终均未破坏；在较小动应力下试样累积塑性应变也最小。

总体来说，加载、间歇均排水，加载不排水、间歇排水，加载、间歇均不排水3 种情况在相同含水率和应力条件下土体的累积塑性变形依次增大，破坏时间也逐步提早，说明3 种条件下土体抗剪强度依次降低。

为研究排水条件与间歇效应的共同效应，以加载，间歇均不排水，σ3=30 kPa，σd=30 kPa 饱和试样为例，统计各阶段的最大累积应变εcp，间歇后累积应变εip和应变恢复率ζ 如表4。由表4 可知，第1阶段恢复的应变最少，为17%，之后各阶段逐渐增大。第4，第5 阶段达到了30%以上，说明随着振次和阶段数增加，土体逐渐被压密，变形逐渐以弹黏性变形为主，间歇阶段累积塑性应变越来越小。这与王军等[14]关于饱和软黏土的结论一致，证实了间歇存在可使土体的弹性变形充分恢复，特别是对排水条件不佳的土体的影响更加显著。