既有结构时变可靠度预测模型及计算方法研究

陈梦成，张明阳，方苇，杨超，李骐，温清清，谈勇，彭爱红，游勇利

（1. 华东交通大学土木建筑学院，江西 南昌 330013；2. 华东交通大学省部共建轨道基础设施性能监测和保障国家重点实验室，江西 南昌 330013；3. 江西交通职业技术学院建筑工程学院，江西 南昌 330013；4. 江西省交通运输厅高速公路管理处，江西 南昌330036；5. 江西省交通工程集团建设有限公司，江西 南昌 330006；6. 江西省公路科研设计院，江西 南昌 330002;7. 江西省嘉和工程咨询监理有限公司，江西 南昌 330009）

既有钢筋混凝土桥梁的时变可靠度评估主要可归结为三个方面：抗力退化时变模型建立、荷载时变模型建立以及时变可靠度计算方法。 本文首先阐述既有钢筋混凝土桥梁结构抗力退化随机过程Gamma 模型、荷载随机过程Poisson 模型，然后构建基于双随机过程的极限状态函数，并建立蒙特卡洛抽样时变可靠度计算方法，最后，以某现服役钢筋混凝土梁式桥为例，对梁式桥服役期为20 a 与服役期为50 a 时的时变可靠性进行了分析。

1 抗力退化随机模型

桥梁结构在服役期间， 因受到可变荷载和振动、极端天气条件、除冰盐和冻融循环以及海洋环境中空气中氯化物等因素影响， 将会导致其结构性能退化。 近些年来，国内外对这方面进行了很多的相关研究[1-12]，提出了众多的桥梁结构抗力退化模型。

本文采用基于Gamma 过程的抗力随机退化模型描述桥梁结构的抗力退化

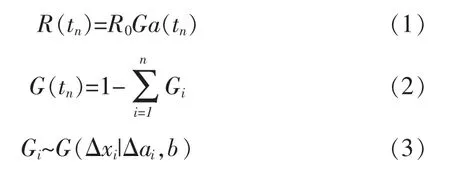
式中：R0为初始时刻抗力；R（tn）为tn时刻抗力；G（tn）为抗力退化系数；Gi为服从Gamma 分布的概率密度函数，随机变量是ΔX（t），它描述的是：抗力退化为独立增量随机过程；Δai为形状参数，b 为尺度参数；Γ（·）表示Gamma 函数；k 是退化参数，α 值根据主要的退化机制确定，如腐蚀（α=1）、硫酸盐侵蚀（α=2）和扩散控制时效（α=0.5）。

根据式（1）～式（5）可以估算桥梁结构任一时刻的抗力值。

2 荷载随机模型

荷载是影响桥梁结构可靠性以及寿命的另一个重要因素。 在桥梁荷载中，有一类荷载，大小随时间变化很小，或者不变化，这就是恒载，譬如说桥梁自重，其大小是随机的，通常考虑为一个服从正态状态分布的随机变量。 另外，还有一类荷载是随机发生的，其大小也是随机的，作用在桥梁上的时间非常短，这就是活载，容易引起桥梁结构发生损伤。 如果荷载效应在其发生的间隔期间变化很小或很慢， 为便于进行可靠性分析，可以认为它的大小是一个不变的量，即认为其对结构的影响基本上是静态的。 与桥梁服役寿命时间相比， 重要荷载在桥梁上出现的的持续时间非常短，而且出现的时间间隔可以认为服从指数分布。 如图1 所示， 结构荷载效应随机过程模拟为一系列随机出现的脉冲，脉冲的大小为Sj，可以用滤过Poisson过程来描述[13]。 fR（r）为抗力的概率密度函数，fS（s）为荷载的概率密度函数；μR（t） 为抗力的均值变化曲线，μS（t）为荷载的均值变化曲线；T1为生命周期。

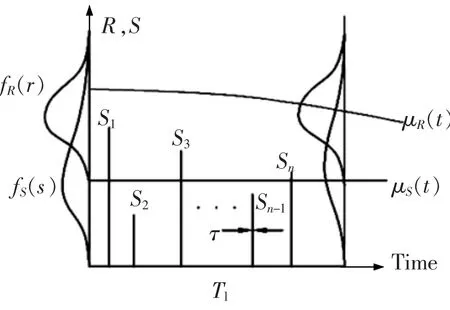
图1 荷载随机过程模型[17]Fig.1 Load stochastic process model[17]

根据滤过泊松过程模型， 在任一时长τ 的区间（0，τ）内，发生车辆荷载次数N（τ）的概率为

式中：λ 为单位时间内荷载的平均发生次数。 假设在时长τ 内发生n 次最不利荷载效应序列Si，i=1，…，n，它们相互独立且服从同一分布。 根据相关研究[7-9]，我们假定Sj服从极值Ⅰ型分布，则其概率分布函数为

式中：γ 为欧拉常数，其值为0.577 215。

3 基于双随机过程的时变可靠度计算方法

桥梁结构的安全性可以用其可靠概率来衡量

式中：FS（r）是荷载效应的概率分布函数；L（T）为寿命T 内的可靠概率；P（·）为概率。

如前文所述， 结构荷载效应和抗力均随时间发生变化，这使得结构的可靠度随时间也发生变化。 为了研究结构的时变可靠度，我们可假设寿命基准期TL内可以分为L 个时间长度为τ 的相等的时间段，时间段序列为（0，t1），（t1，t2），…，（tL-1，tL）。 假定结构失效模式为串联模式，则其可靠概率可以表示为

3.1 结构时段有效概率

根据Poisson 过程模型，确定在任一时段i 区间（ti-1，ti）内发生n 次最不利荷载效应Sij（j=1，…，n），并记下相应的发生时刻为tij， 则该时段内结构可靠概率PSi为

若考虑最n 个不利荷载效应Sij在时段长度τ（tL-1，tL）内发生的时刻tij是一个随机变量，而且服从同一分布和相互独立， 概率密度函数记为fT（t）。一般假定Sij在时段长τ（tL-1，tL）内发生的时刻tij服从均匀分布，则式（11）改写为

3.2 时段内结构失效概率

根据概率的性质， 我们可以得到结构在时段（tL-1，tL）内的失效概率Pfi为

3.3 寿命基准期内总失效概率

根据各时段失效概率Pfi，（i=1，…，L）和式（10），我们即可得到寿命基准期TL内桥梁结构的总失效概率Pf（TL）为

若假定每个时段τ（ti-1，ti）内结构荷载效应和抗力均相互独立, 这里笔者作出独立性假设的依据是：一方面,结构在各时点的抗力之间是相关的，但其相关性很难分析，将在另文阐述这方面的研究;另一方面，采用独立的抗力与荷载模型， 可得到更加偏于保守，安全的结果[14]。 根据独立性假设，则式（19）可变形为

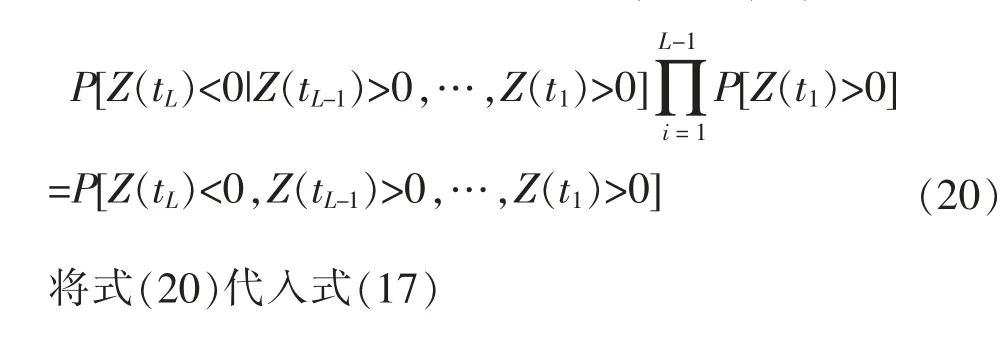
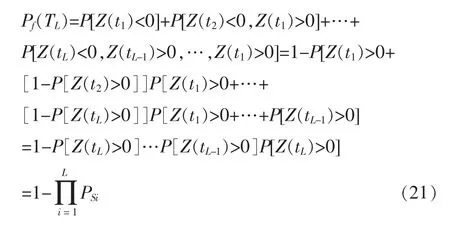
3.4 计算周期内可靠指标

假定在时段τ（ti-1，ti）内，时变可靠度指标用β（ti）来描述，则根据可靠度指标定义Pf=Φ（-β）有

应该指出的是，这里的时变可靠性指标β（ti）仅仅是借用了基于设计基准期可靠性指标的定义，与其实际含义是不同的[15]。

4 蒙特卡洛抽样法（MCS）

一般地，式（15）采用直接积分的方法很难被计算出来，随着计算机计算机技术的发展，蒙特卡洛模拟（Monte Carlo simulation，MCS）方法越来越多地用于计算此类问题。 MCS 的原理是：对工程结构的抗力与荷载效应进行多次抽样，这样得到多个结构状态，然后将Z<0 的状态进行统计，即计算失效的次数占抽样总次数的比值为结构的失效概率。 本文采用MCS 方法计算基于双随机过程的时变可靠度计算。 MCS 方法的计算步骤为：

1） 随机抗力初始值R0的样本；

2） 寿命基准期TL内可以分为L 个时间长度为τ 的相等的时间段，时间段序列为（0，t1），（t1，t2），…，（tL-1，tL）；

3） 对每一段时间序列（ti-1，ti）生成一个均值为λτ 的的泊松数n，然后生成n 个在时间序列（ti-1，ti）均匀，独立分布的时刻tj，j=1，…，n；

4） 对应tj，j=1，…，n 时刻，随机生成荷载效应样本值Sij及抗力样本值R0G（tij）；

5） 若对抽取的Sij与R0G（tij）均满足R0G（tij）≥Sij，则说明结构安全，否则结构失效；

本文采用的改进的时变可靠度Monte Carlo 计算方法与传统的时变可靠度计算方法相比， 增加了第2 步与第3 步， 这样做的目的是将计算期的每个阶段随机划分为N 段， 然后计算每一段的失效概率，进而计算整个计算周期内的失效概率。

5 算例分析

算例1：本文算例来自于文献[16]，工程概况：某现服役钢筋混凝土梁式桥，其横断面如图7 所示。主梁为T 型截面。梁混凝土等级为C30，钢筋等级为二级钢（HRB335），跨径为15.5 m。

图2 某桥梁断面[16]（单位：cm）Fig.2 Cross section of an illustrative bridge[16]（Unit：cm）

依据《公路桥梁承载能力检测评定规程》，考虑桥梁结构随时间退化，可评估出上述桥梁结构当前实际承载能力（抗力），R0为2 530 kN·m。考虑到R0的不确定性，根据Ellingwood[17]的研究，抗力R0服从对数正态分布，其变异系数为0.15。 本算例跨中截面最大弯矩（荷载效应）的均值和标准差分别为1 020 kN·m 和240 kN·m。

为验证本方法的有效性，采用与文献[16]一样的抗力退化模型。 即Enright[18]的混凝土抗力退化的确定性模型

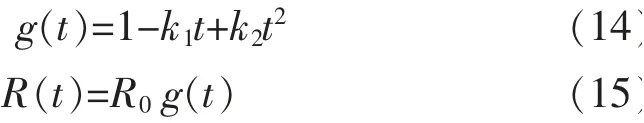
式 中：k1，k2为 承 载 力 退 化 速 度；t 为 退 化 时 间，a；k1，k2取值表示不同退化速率模型，如下所示

式中：T 为起始退化时间，a。慢速退化模型与中速退化模型为线性回归模型， 快速退化模型为非线性模型。 当退化T=20 a 时，基于慢速、中速、快速三种退化情形分别计算该桥梁时变可靠度， 计算得到的失效概率、 可靠度β 与时间的关系如图3所示。 从图3 中可见，改进的MC 方法与文献[18]的MC 方法的计算结果吻合很好。 以慢速退化退化机制下的T=20 a 时的可靠度指标为例，本文方法：β（20）=2.093 7，传统方法：β（20）=2.118 7，两者相差1.18%，由此证明了本方法的准确性。并当改进的MC 方法与普通的MC 方法抽取次数均为ns=106时，3 种情况下，2 种方法所用时间如表1所示。

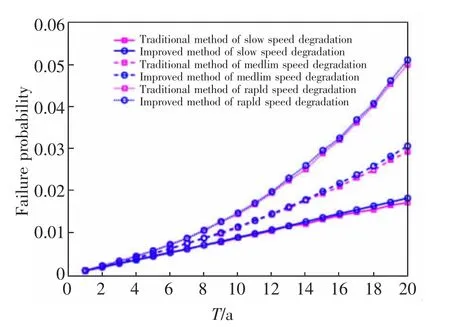
图3 两种方法的各种退化模型失效概率Fig.3 Failure probability of various degradation models of the two methods

图4 两种方法的各种退化模型可靠度Fig.4 Reliability of various degradation models of the two methods

表1 两种方法的计算时间Tab.1 calculation time of two methods

从表1 可以看出一般方法所用时间为本文方法所用时间近乎4 倍，这体现了本方法的高效性。

算例2：采用基于Gamma 过程的抗力随机退化模型描述桥梁结构的抗力退化，如式（1）～式（5）所示，其中考虑三种抗力退化机制：腐蚀（α=1）、硫酸盐侵蚀（α=2）和扩散控制时效（α=0.5）。 本算例采用服役期20 a后抗力劣化系数均值与上述快速退化机制下得一致，即为G（20）=0.82。 则取对于腐蚀机制引起的线性劣化（α=1），参数b=0.147 和k=0.061 2。 对于平方根恶化（α=0.5），b=0.147，k=0.274，对于抛物线退化（α=2），b=0.147，k=0.003 06；对于以上3 种退化机制，分别计算该桥梁的失效概率、可靠度β 与时间的关系，并与传统的时变可靠度计算方法进行对比，如图5，图6 所示。

从图5，图6 中可见，改进的时变可靠度计算方法与传统的计算方法的结果吻合很好。 以抛物线退化机制下的T=20 a 时的可靠度指标为例， 本文方法：β（20）＝0.952 2，传统方法：β（20）＝0.935 9，两者相差1.7%，由此证明了本方法的准确性。 并当本文方法与传统的时变可靠度计算方法抽取次数均为ns=106时，3 种情况下，2 种方法所用时间如表2 所示。

图5 两种方法的各种退化模型失效概率Fig.5 Failure probability of various degradation models of the two methods

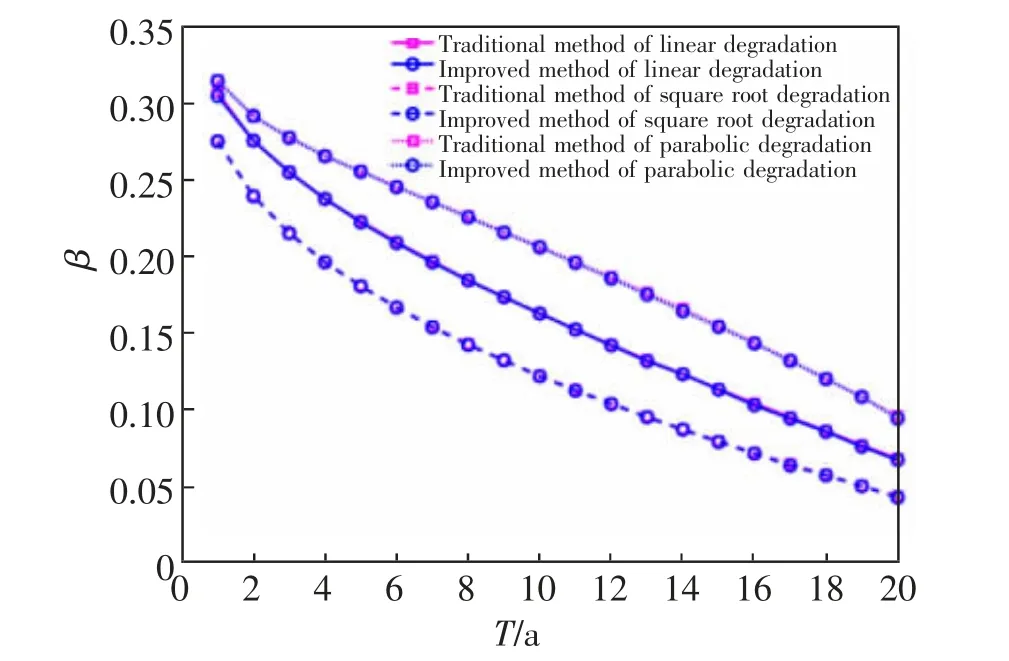
图6 两种方法的各种退化模型可靠度Fig.6 Reliability of various degradation models of the two methods

表2 2 种方法的计算时间Tab.2 calculation time of two methods

从表2 可以看出普通的时变可靠度方法所用时间为本文方法所用时间近乎4 倍甚至更多，这体现了本方法的高效性。

另外，我们可以对该桥梁的失效概率与可靠指标做出预测。 以腐蚀机制下的桥梁抗力退化模型为例，预测得到桥梁在后30 a 的失效概率以及可靠指标，如图7，图8 所示。 并将T=30，40，50 a 时的预测失效概率与可靠指标列于表3 中。

表3 预测腐蚀机制下的桥梁时变可靠度Tab.3 Prediction of time-varying reliability of bridges under corrosion mechanism

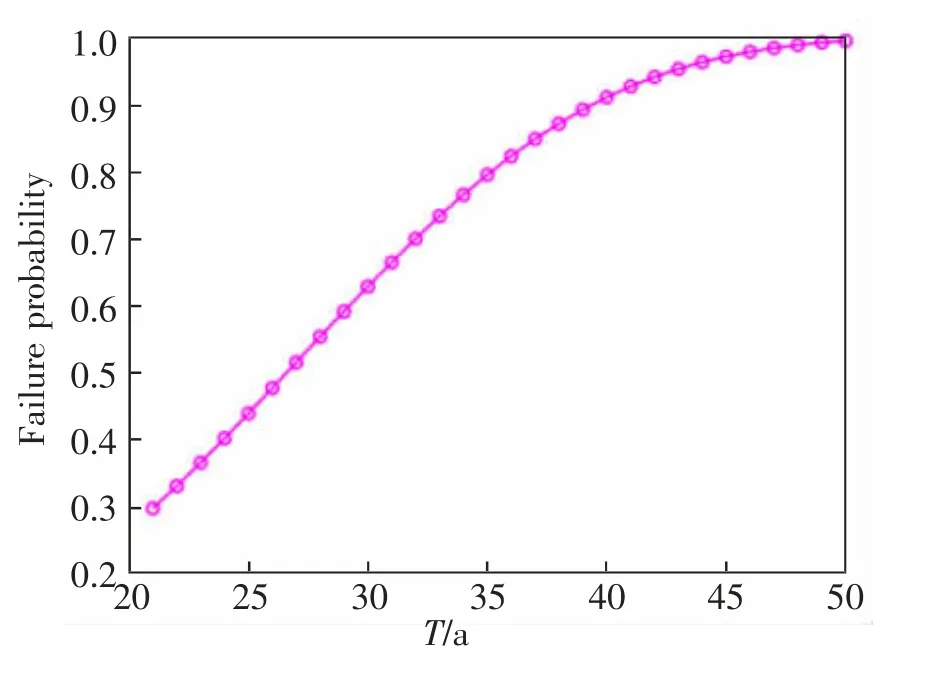
图7 腐蚀机制下的桥梁预测失效概率Fig.7 predicted failure probability of bridge under corrosion mechanism

图8 腐蚀机制下的桥梁预测可靠指标Fig.8 predicted reliability indexof bridge under corrosion mechanism

从图7，图8，表3 中可以看出，可以在既有结构的基础上，建立抗力的随机过程模型，并利用该方法对桥梁结构的失效概率与可靠指标进行预测。

6 结论

本文的一个主要工作是构建了一个适用于实际工程，考虑抗力-荷载双随机过程的理论模型，并基于抗力和荷载效应相互独立的基本假定，使用条件概率公式， 严格得到了结构失效概率计算表达式。 进而提出了基于抗力-荷载双随机过程模型的改进的时变可靠度计算方法。 该方法将计算期的每个阶段随机划分为N 段，然后计算每一段的失效概率，进而计算整个计算周期内的失效概率。 使用该方法计算了某现服役钢筋混凝土梁式桥20 a 在2种不同抗力退化模型下以及预测腐蚀机制退化模型的后30 a 时的失效概率可靠度。 通过计算与分析，得到以下结论。

1） 本方法可计算荷载与抗力均为随机过程的时变可靠度， 算例表明了本方法的准确性与高效性。 利用该方法给出的可靠度计算结果与普通方法给出的“精确”相比误差不超过1%，但计算时间仅为普通方法的1/5～1/3，且当桥梁使用期限越长时，该方法的高效性越显著。

2） 本文将荷载效应与各个时间点上的抗力退化均描述为是相互独立的。 但事实上，抗力退化过程本身，荷载之间，荷载与抗力之间是相关的。 如何考虑它们之间的相关性， 拟作为下一步研究的重点。